广东省广州市六校2023届高三下学期第四次联考(开学考试)数学试卷(含答案)
文档属性
| 名称 | 广东省广州市六校2023届高三下学期第四次联考(开学考试)数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 886.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 14:27:23 | ||
图片预览




文档简介
广东省广州市六校2023届高三下学期第四次联考(开学考试)数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知集合,集合,则( )
A. B. C. D.
2、如图,在复平面内,复数z对应的点为P,则复数的虚部为( )
A. B. C. D.
3、已知,是空间中两个不同的平面,m,n是空间中两条不同的直线,则下列命题中正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,,则
4、已知数列的前n项和为,数列是递增数列是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5、八角星纹是大汶口文化中期彩陶纹样中具有鲜明特色的花纹.八角星纹常绘于彩陶盆和豆的上腹,先于器外的上腹施一圈红色底衬,然后在上面绘并列的八角星形的单独纹样.八角星纹以白彩的成,黑线勾边,中为方形或圆形,且有向四面八方扩张的感觉.八角星纹延续的时间较长,传播范围亦广,在长江以南的时间稍晚的崧泽文化的陶豆座上也屡见刻有八角大汶口文化八角星纹.图2是图1抽象出来的图形,在图2中,圆中各个三角形(如)为等腰直角三角形,点O为四心,中间部分是正方形且边长为2,定点A,B所在位置如图所示,则的值为( )
图1 图2
A.10 B.12 C.14 D.16
6、把二项式的所有展开项重新排列,求有理项不相邻的概率为( )
A. B. C. D.
7、已知双曲线的左,右焦点分别为,,记,以坐标原点O为圆心,c为半径的圆与双曲线M在第一象限的交点为P.若,则双曲线的离心率为( )
A. B. C. D.
8、已知函数对任意的,恒成立,则实数a的取值范围为( )
A. B. C. D.
二、多项选择题
9、已知的图象可由的图象向右平移个单位长度得到,则下列说法正确的是( )
A.的最小正周期为
B.在上单调递增
C.当时,的取值范围为
D.是偶函数
10、若抛物线的焦点为F,准线为l,点M在抛物线C上且在第一象限,直线MF的斜率为,M在直线l上的射影为A,则下列选项正确的是( )
A.F到直线的距离为 B.的面积为
C.AF的垂直平分线过点M D.以MF为直径的圆过点
11、已知函数,则下列结论正确的是( )
A.函数只有两个极值点
B.方程有且只有两个实根,则的取值范围为
C.方程共有4个根
D.若,,则的最大值为2
12、如图,矩形ABCD中,,,E为边AB的中点,沿DE将折起,点A折至处(平面ABCD),若M为线段AC的中点,平面ADE与平面DEBC所成锐二面角,直线AE与平面DEBC所成角为,则在折起过程中,下列说法正确的是( )
A.存在某个位置,使得
B.面积的最大值为
C.
D.三棱锥体积最大时,三棱锥的外接球的表面积
三、填空题
13、已知,,且,则的最小值是______.
14、若斜率为的直线与y轴交于点A,与圆相切于点B,则______.
15、某公司在某地区进行商品的调查,随机调查了100位购买商品A的顾客的性别,其中男性顾客18位,已知该地区商品A的购买率为10%,该地区女性人口占该地区总人口的46%,从该地区中任选一人,若此人是男性,求此人购买商品A的概率______
16、数列中,表示自然数的所有因数中最大的那个奇数,例如:20的因数有1,2,4,5,10,20,,21的因数有1,3,7,21,,那么数列前项的和______
四、解答题
17、已知等差数列的前n项和为,数列是公比为2的等比数列,且,,
(1)求数列,的通项公式;
(2)数列与中的所有项分别构成集合A,B,将集合中的所有元素从小到大依次排列构成新数列,求数列的前20项和
18、已知的角A,B,C的对边分别为a,b,c,且,
(1)求角A;
(2)若AD平分交线段BC于点D,且,,求的周长.
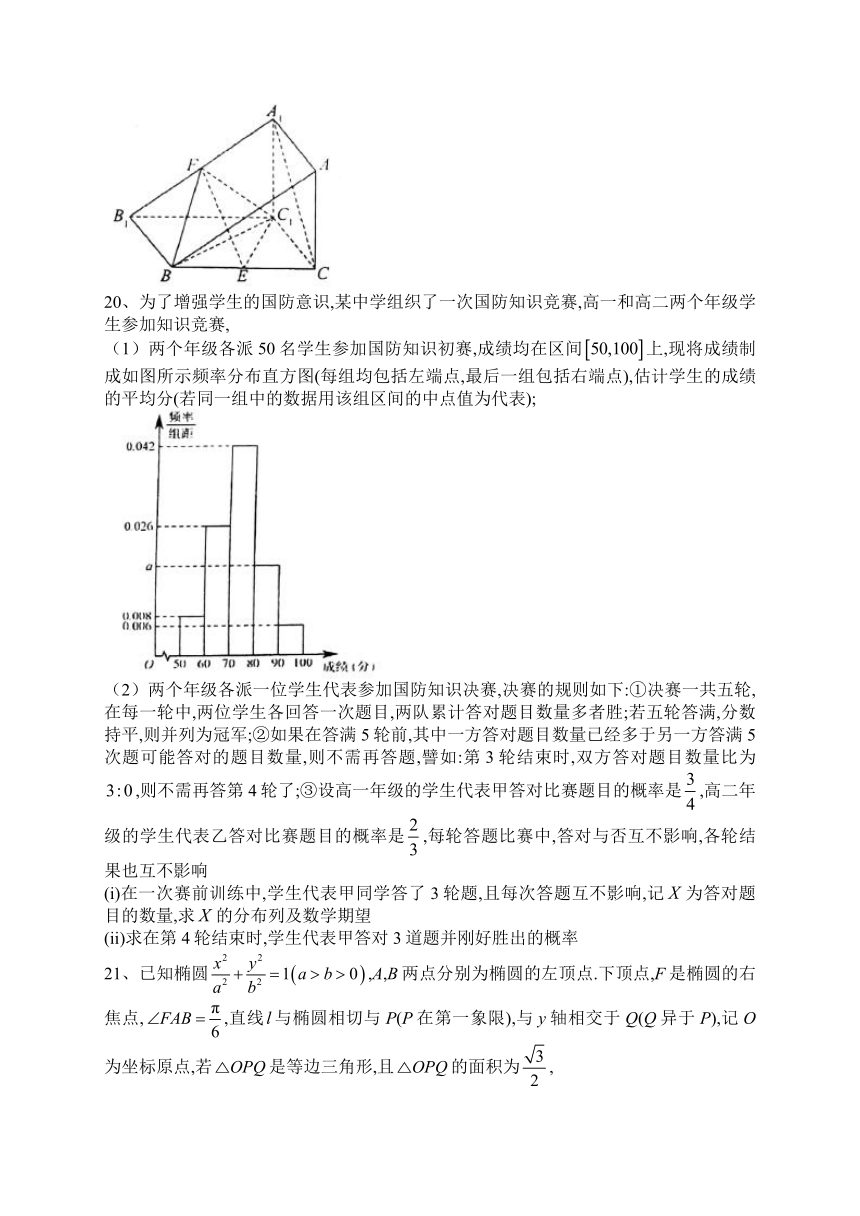
19、如图,在三棱柱中,平面平面,侧面是边长为2的正方形,,,E.F分别为BC.的中点
(1)求证:
(2)求二面角的余弦值.
20、为了增强学生的国防意识,某中学组织了一次国防知识竞赛,高一和高二两个年级学生参加知识竞赛,
(1)两个年级各派50名学生参加国防知识初赛,成绩均在区间上,现将成绩制成如图所示频率分布直方图(每组均包括左端点,最后一组包括右端点),估计学生的成绩的平均分(若同一组中的数据用该组区间的中点值为代表);
(2)两个年级各派一位学生代表参加国防知识决赛,决赛的规则如下:①决赛一共五轮,在每一轮中,两位学生各回答一次题目,两队累计答对题目数量多者胜;若五轮答满,分数持平,则并列为冠军;②如果在答满5轮前,其中一方答对题目数量已经多于另一方答满5次题可能答对的题目数量,则不需再答题,譬如:第3轮结束时,双方答对题目数量比为,则不需再答第4轮了;③设高一年级的学生代表甲答对比赛题目的概率是,高二年级的学生代表乙答对比赛题目的概率是,每轮答题比赛中,答对与否互不影响,各轮结果也互不影响
(i)在一次赛前训练中,学生代表甲同学答了3轮题,且每次答题互不影响,记为答对题目的数量,求的分布列及数学期望
(ii)求在第4轮结束时,学生代表甲答对3道题并刚好胜出的概率
21、已知椭圆,A,B两点分别为椭圆的左顶点.下顶点,F是椭圆的右焦点,,直线与椭圆相切与P(P在第一象限),与y轴相交于Q(Q异于P),记O为坐标原点,若是等边三角形,且的面积为,
(1)求椭圆的标准方程;
(2)C,D两点均在直线,且C在第一象限,设直线AD,BC分别交椭圆于点S,点T,若S,T关于原点对称,求的最小值
22、已知函数有两个零点,,且,
(1)求的取值范围;
(2)证明:
参考答案
1、答案:C
解析:略
2、答案:B
解析:由图形知,点,则复数,
故,所以复数的虚部为 .故选:B.
3、答案:D
解析:对于A选项,若,,则或,A错;
对于B选项,若,,则或,相交,B错;
对于C选项,若,,则或或m,相交(不一定垂直),C错;
对于D选项,设直线m,n的方向向量分别为,
若,,,则平面,的一个法向量分别为,,且,故,D对.故选:D.
4、答案:D
解析:若是等比数列,且,,则数列是递增数列,但,若,有可能,,则数列不是单调数列,则数列是递增数列是的既不充分也不必要条件.故选:D.
5、答案:C
解析:如图所示:连接OD,
因为中间阴影部分是正方形且边长为2,且图中各个三角形为等腰直角三角形,所以可得,,,,
则,故选:C.
6、答案:B
解析:,其中,
当,3,6,9,项为有理项,则有4项有理项,6项无理项,展开式的10项全排列共有的,有理项互不相邻可把6个无理项全排把4个有理项在形成的7个空中插空即可,有种,有理项都互不相邻的概率为,故选:B.
7、答案:A
解析:略
8、答案:B
解析:略
9、答案:AB
解析:由函数的图象向右平移个单位长度得到函数的图象;对于A:函数的最小正周期为Error! Digit expected.,故A正确;
对于B:由于,故Error! Digit expected.,故函数在该区间上单调递增,故B正确;
对于C:当时,的取值范围为,故C错误
对于D:由于,故满足故该函数为奇函数,故D错误.故选:AB.
10、答案:BC
解析:略
11、答案:ACD
解析:略
12、答案:BCD
解析:略
13、答案:25
解析:
,,,,,Error! Digit expected.,
则.
当且仅当时,即,即,时取等号.Error! Digit expected.的最小值为25.
14、答案:
解析:假设A在x轴的上方,斜率为的直线与x轴交于D,则可得,所以,如图所示,
由圆C的方程可得,圆的半径为,由于B为切点,所以,所以,故答案为:.
15、答案:
解析:设从该地区中任选一人,此人是男性为事件B,此人购买商品A为事件C,则该地区男性人口占该地区总人口的Error! Digit expected.,则,由条件概率公式可得.故答案为:.
16、答案:
解析:略
17、答案:(1)
(2)270
解析:(1)数列为等差数列,且,
,即,,即
数列是公比为2的等比数列,,
即
(2)由(1)知,数列的元素是由数列中去除数列
数列中去掉2,4,8,16,
18、答案:(1)
(2)
解析:(1)由余弦定理得
所以可化为
再由正弦定理得,得.
所以,因为,所以
(2)因为平分,所以
由,
得
作于,则
由,解得
由余弦定理,得,所以
故的周长为
19、答案:(1)见解析
(2)
解析:(1)证明:面面,面面,
,面
面,
面,
又,
面
取的中点G,连接FG,CG,
面
又,,
四边形EFGC为平行四边形
(2)面,
如图,以为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
则,,,
,,
设平面的一个法向量为,则
可取,
设平面的一个法向量为,
则,
可取
设二面角为,
则
所以二面角的余弦值为
20、答案:(1)
(2)
解析:(1)由频率分布直方图可知:可得
平均分的估计值为
学生的成绩的平均分的估计值为73.8分
(2)(i)由题可得.,X的可能取值为0,1,2,3
X的分布列为
X 0 1 2 3
P
(2)(ii)将“在第4轮结束时,学生代表甲答对3道题并刚好胜出”记为事件A,
“在第4轮结束时,学生代表乙答对0道题”记为事件,
“在第4轮结束时,学生代表乙答对1道题”记为事件
,
21、答案:(1)
(2)6
解析:(1),则
是等边三角形,,则
,,则,
将代入,,
,解得
椭圆的标准方程为
(2),,,
则直线,
所以
,,则直线
所以,
所以
设,则
,
当且仅当,等号成立,所以,即的最小值为6
22、答案:(1)见解析
(2)见解析
解析:(1)因为的定义域为,所以
当时,恒成立,所以在上单调递增,
故不可能有两个零点,故舍去;
当肘,令,解得
令,解得,
所以在上单调递增,在上单调递减,
所以,要使有两个零点,则
解得
又,,
所以当时,在和上各有一个零点,,
且,所以,
由单调性知,当时,,
当时
因为,所以,即
所以,而,所以,所以
令,
则,所以在上单调递增,
所以,所以
(2)
要证,即证即证
即证
.设,,
,,
令,
令,
在
,在
得证
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知集合,集合,则( )
A. B. C. D.
2、如图,在复平面内,复数z对应的点为P,则复数的虚部为( )
A. B. C. D.
3、已知,是空间中两个不同的平面,m,n是空间中两条不同的直线,则下列命题中正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,,则
4、已知数列的前n项和为,数列是递增数列是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5、八角星纹是大汶口文化中期彩陶纹样中具有鲜明特色的花纹.八角星纹常绘于彩陶盆和豆的上腹,先于器外的上腹施一圈红色底衬,然后在上面绘并列的八角星形的单独纹样.八角星纹以白彩的成,黑线勾边,中为方形或圆形,且有向四面八方扩张的感觉.八角星纹延续的时间较长,传播范围亦广,在长江以南的时间稍晚的崧泽文化的陶豆座上也屡见刻有八角大汶口文化八角星纹.图2是图1抽象出来的图形,在图2中,圆中各个三角形(如)为等腰直角三角形,点O为四心,中间部分是正方形且边长为2,定点A,B所在位置如图所示,则的值为( )
图1 图2
A.10 B.12 C.14 D.16
6、把二项式的所有展开项重新排列,求有理项不相邻的概率为( )
A. B. C. D.
7、已知双曲线的左,右焦点分别为,,记,以坐标原点O为圆心,c为半径的圆与双曲线M在第一象限的交点为P.若,则双曲线的离心率为( )
A. B. C. D.
8、已知函数对任意的,恒成立,则实数a的取值范围为( )
A. B. C. D.
二、多项选择题
9、已知的图象可由的图象向右平移个单位长度得到,则下列说法正确的是( )
A.的最小正周期为
B.在上单调递增
C.当时,的取值范围为
D.是偶函数
10、若抛物线的焦点为F,准线为l,点M在抛物线C上且在第一象限,直线MF的斜率为,M在直线l上的射影为A,则下列选项正确的是( )
A.F到直线的距离为 B.的面积为
C.AF的垂直平分线过点M D.以MF为直径的圆过点
11、已知函数,则下列结论正确的是( )
A.函数只有两个极值点
B.方程有且只有两个实根,则的取值范围为
C.方程共有4个根
D.若,,则的最大值为2
12、如图,矩形ABCD中,,,E为边AB的中点,沿DE将折起,点A折至处(平面ABCD),若M为线段AC的中点,平面ADE与平面DEBC所成锐二面角,直线AE与平面DEBC所成角为,则在折起过程中,下列说法正确的是( )
A.存在某个位置,使得
B.面积的最大值为
C.
D.三棱锥体积最大时,三棱锥的外接球的表面积
三、填空题
13、已知,,且,则的最小值是______.
14、若斜率为的直线与y轴交于点A,与圆相切于点B,则______.
15、某公司在某地区进行商品的调查,随机调查了100位购买商品A的顾客的性别,其中男性顾客18位,已知该地区商品A的购买率为10%,该地区女性人口占该地区总人口的46%,从该地区中任选一人,若此人是男性,求此人购买商品A的概率______
16、数列中,表示自然数的所有因数中最大的那个奇数,例如:20的因数有1,2,4,5,10,20,,21的因数有1,3,7,21,,那么数列前项的和______
四、解答题
17、已知等差数列的前n项和为,数列是公比为2的等比数列,且,,
(1)求数列,的通项公式;
(2)数列与中的所有项分别构成集合A,B,将集合中的所有元素从小到大依次排列构成新数列,求数列的前20项和
18、已知的角A,B,C的对边分别为a,b,c,且,
(1)求角A;
(2)若AD平分交线段BC于点D,且,,求的周长.
19、如图,在三棱柱中,平面平面,侧面是边长为2的正方形,,,E.F分别为BC.的中点
(1)求证:
(2)求二面角的余弦值.
20、为了增强学生的国防意识,某中学组织了一次国防知识竞赛,高一和高二两个年级学生参加知识竞赛,
(1)两个年级各派50名学生参加国防知识初赛,成绩均在区间上,现将成绩制成如图所示频率分布直方图(每组均包括左端点,最后一组包括右端点),估计学生的成绩的平均分(若同一组中的数据用该组区间的中点值为代表);
(2)两个年级各派一位学生代表参加国防知识决赛,决赛的规则如下:①决赛一共五轮,在每一轮中,两位学生各回答一次题目,两队累计答对题目数量多者胜;若五轮答满,分数持平,则并列为冠军;②如果在答满5轮前,其中一方答对题目数量已经多于另一方答满5次题可能答对的题目数量,则不需再答题,譬如:第3轮结束时,双方答对题目数量比为,则不需再答第4轮了;③设高一年级的学生代表甲答对比赛题目的概率是,高二年级的学生代表乙答对比赛题目的概率是,每轮答题比赛中,答对与否互不影响,各轮结果也互不影响
(i)在一次赛前训练中,学生代表甲同学答了3轮题,且每次答题互不影响,记为答对题目的数量,求的分布列及数学期望
(ii)求在第4轮结束时,学生代表甲答对3道题并刚好胜出的概率
21、已知椭圆,A,B两点分别为椭圆的左顶点.下顶点,F是椭圆的右焦点,,直线与椭圆相切与P(P在第一象限),与y轴相交于Q(Q异于P),记O为坐标原点,若是等边三角形,且的面积为,
(1)求椭圆的标准方程;
(2)C,D两点均在直线,且C在第一象限,设直线AD,BC分别交椭圆于点S,点T,若S,T关于原点对称,求的最小值
22、已知函数有两个零点,,且,
(1)求的取值范围;
(2)证明:
参考答案
1、答案:C
解析:略
2、答案:B
解析:由图形知,点,则复数,
故,所以复数的虚部为 .故选:B.
3、答案:D
解析:对于A选项,若,,则或,A错;
对于B选项,若,,则或,相交,B错;
对于C选项,若,,则或或m,相交(不一定垂直),C错;
对于D选项,设直线m,n的方向向量分别为,
若,,,则平面,的一个法向量分别为,,且,故,D对.故选:D.
4、答案:D
解析:若是等比数列,且,,则数列是递增数列,但,若,有可能,,则数列不是单调数列,则数列是递增数列是的既不充分也不必要条件.故选:D.
5、答案:C
解析:如图所示:连接OD,
因为中间阴影部分是正方形且边长为2,且图中各个三角形为等腰直角三角形,所以可得,,,,
则,故选:C.
6、答案:B
解析:,其中,
当,3,6,9,项为有理项,则有4项有理项,6项无理项,展开式的10项全排列共有的,有理项互不相邻可把6个无理项全排把4个有理项在形成的7个空中插空即可,有种,有理项都互不相邻的概率为,故选:B.
7、答案:A
解析:略
8、答案:B
解析:略
9、答案:AB
解析:由函数的图象向右平移个单位长度得到函数的图象;对于A:函数的最小正周期为Error! Digit expected.,故A正确;
对于B:由于,故Error! Digit expected.,故函数在该区间上单调递增,故B正确;
对于C:当时,的取值范围为,故C错误
对于D:由于,故满足故该函数为奇函数,故D错误.故选:AB.
10、答案:BC
解析:略
11、答案:ACD
解析:略
12、答案:BCD
解析:略
13、答案:25
解析:
,,,,,Error! Digit expected.,
则.
当且仅当时,即,即,时取等号.Error! Digit expected.的最小值为25.
14、答案:
解析:假设A在x轴的上方,斜率为的直线与x轴交于D,则可得,所以,如图所示,
由圆C的方程可得,圆的半径为,由于B为切点,所以,所以,故答案为:.
15、答案:
解析:设从该地区中任选一人,此人是男性为事件B,此人购买商品A为事件C,则该地区男性人口占该地区总人口的Error! Digit expected.,则,由条件概率公式可得.故答案为:.
16、答案:
解析:略
17、答案:(1)
(2)270
解析:(1)数列为等差数列,且,
,即,,即
数列是公比为2的等比数列,,
即
(2)由(1)知,数列的元素是由数列中去除数列
数列中去掉2,4,8,16,
18、答案:(1)
(2)
解析:(1)由余弦定理得
所以可化为
再由正弦定理得,得.
所以,因为,所以
(2)因为平分,所以
由,
得
作于,则
由,解得
由余弦定理,得,所以
故的周长为
19、答案:(1)见解析
(2)
解析:(1)证明:面面,面面,
,面
面,
面,
又,
面
取的中点G,连接FG,CG,
面
又,,
四边形EFGC为平行四边形
(2)面,
如图,以为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
则,,,
,,
设平面的一个法向量为,则
可取,
设平面的一个法向量为,
则,
可取
设二面角为,
则
所以二面角的余弦值为
20、答案:(1)
(2)
解析:(1)由频率分布直方图可知:可得
平均分的估计值为
学生的成绩的平均分的估计值为73.8分
(2)(i)由题可得.,X的可能取值为0,1,2,3
X的分布列为
X 0 1 2 3
P
(2)(ii)将“在第4轮结束时,学生代表甲答对3道题并刚好胜出”记为事件A,
“在第4轮结束时,学生代表乙答对0道题”记为事件,
“在第4轮结束时,学生代表乙答对1道题”记为事件
,
21、答案:(1)
(2)6
解析:(1),则
是等边三角形,,则
,,则,
将代入,,
,解得
椭圆的标准方程为
(2),,,
则直线,
所以
,,则直线
所以,
所以
设,则
,
当且仅当,等号成立,所以,即的最小值为6
22、答案:(1)见解析
(2)见解析
解析:(1)因为的定义域为,所以
当时,恒成立,所以在上单调递增,
故不可能有两个零点,故舍去;
当肘,令,解得
令,解得,
所以在上单调递增,在上单调递减,
所以,要使有两个零点,则
解得
又,,
所以当时,在和上各有一个零点,,
且,所以,
由单调性知,当时,,
当时
因为,所以,即
所以,而,所以,所以
令,
则,所以在上单调递增,
所以,所以
(2)
要证,即证即证
即证
.设,,
,,
令,
令,
在
,在
得证
同课章节目录
