1.5 同底数幂的除法[下学期]

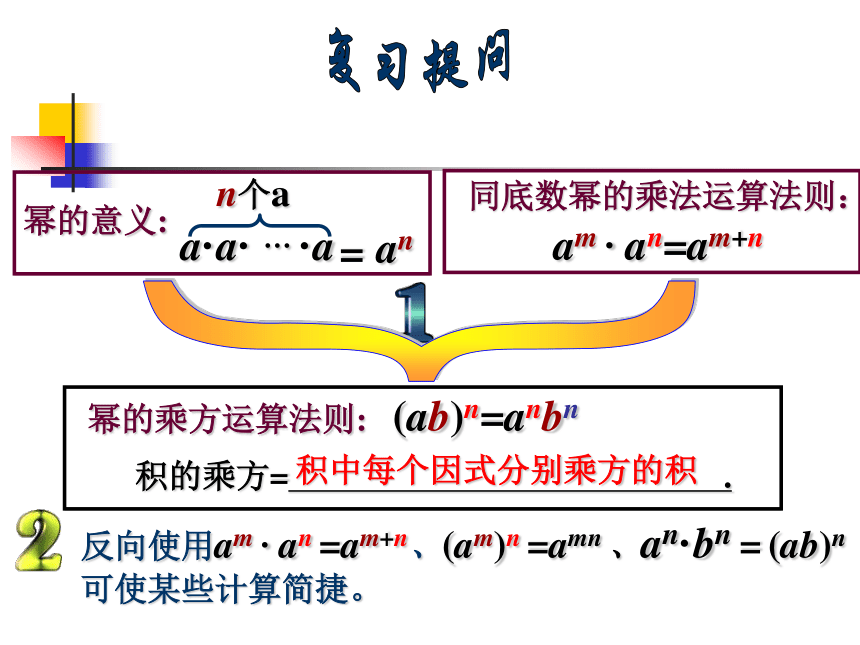
课件31张PPT。 第一章 整式的运算《数学》(北师大.七年级 下册)5同底数幂的除法复习提问积中每个因式分别乘方的积计算杀菌济的滴数 一种液体每升杀死含有1012 个有害细菌，为了试验某种杀菌剂的效果，科学家们进行了实验，发现
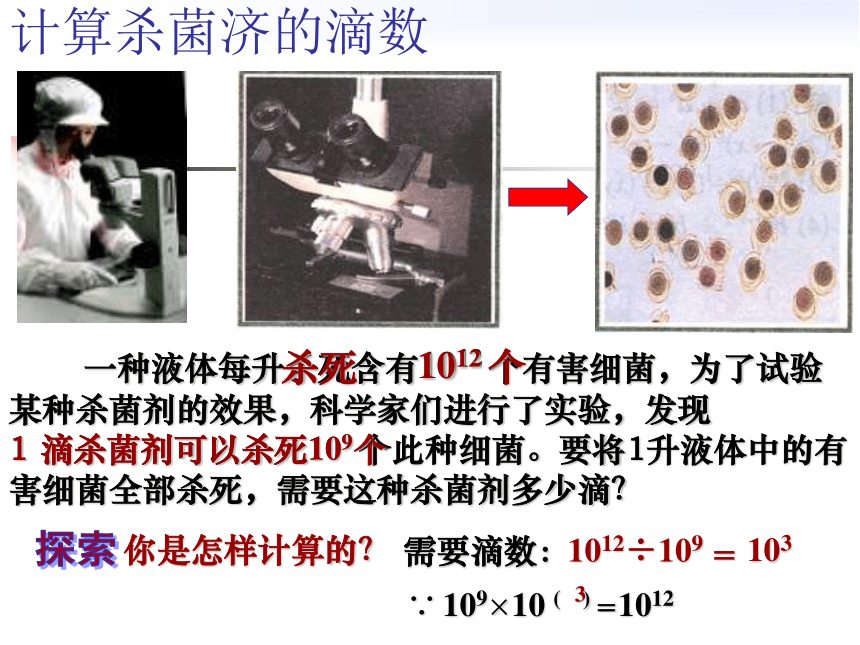
1 滴杀菌剂可以杀死109 个此种细菌。要将1升液体中的有害细菌全部杀死，需要这种杀菌剂多少滴？1 滴杀菌剂可以杀死109个需要滴数：∵ 109×10 ( ) =1012=？31031012÷109用 逆运算与同底数幂的乘法 来计算计算下列各式：
（1）108 ÷105
（2）10m÷10n
（3）(–3)m÷(–3)n3103 ;m–n10m–n ;m–n(–3)m–n ;am–n2、讨论下列问题：
(1)同底数幂相除法则中各这字母必须满足什么条件？a ÷a =(a≠0,m,n都是正整数,且m＞n)mnam-n同底数幂相除，底数_____,指数______. 不变相减am–n不变相减证明: m–nam–n .(法二) 用幂的定义: am÷an=mnm–n= am–n .同底数幂的 除法法则已学过的幂运算性质（1）am·an=am+n (a≠0 ,m、n为正整数)
（2）am÷an=am-n (a≠0 ,m、n为正整数且m>n)
（3）(am)n=amn (a≠0 ,m、n为正整数)
（4）(ab)n=anbn (a≠0 ,n为正整数)例题解析例题解析 【例1】计算：
(1) a7÷a4 ; (2) (-x)6÷(-x)3;
(3) (xy)4÷(xy) ; (4) b2m+2÷b2 . = a7–4 = a3 ;(1) a7÷a4 解：(2) (-x)6÷(-x)3= (-x)6–3 = (-x)3(3) (xy)4÷(xy) =(xy)4–1(4) b2m+2÷b2 = b2m+2 – 2= -x3 ;=(xy)3=x3y3= b2m .最后结果中幂的形式应是最简的.① 幂的指数、底数都应是最简的；② 幂的底数是积的形式时，要再用一次(ab)n=an bn.(5) (m-n)8÷(n-m)31、x8÷(-x2)
2、a3n÷an
3、(y2)3÷y3
4、27÷(-2)3
5、38÷(34.34)=-x6=a2n=y3=27÷(-23)=-24=-16=38÷38=1练一练6、计算
(1)a7÷(a4·a2) (2) (-x)7÷x2
(3) (ab)5÷ (ab)2 (4)a6÷a2· a4
(5)(a+b)6÷ (a+b)4
公式：am÷an=am—n（a≠0,m,n都是正整数，且m＞n）让我们一起给它拓展一下！（1）、m＞n（已学过）
（2）、 m=n
（3）、 m＜n正整数指数幂 的扩充3210–1–2–33210–1–2–3探索与合作学习（1）53÷53=5（ ）－（ ）=5（ ）
又53 ÷53=1
得到_________________
3 3050=1规定 a0=1(a≠0)
任何不等于零的数的零次幂都等于1。
更一般地，a0= ？(a≠0）33235-2问：一般地 a-p = ？任何非零数的零次幂都等于1。任何非零数数的-P(P是正整数)次幂，等于这个数的P次幂的倒数。零指数幂、负指数幂的理解为使“同底数幂的运算法则am÷an=am–n通行无阻：∴ 规定 a0 =1；am–mam÷am=（a≠0, m、n都是正整数）=a0，1==a0÷a p=a0–p=a–p已学过的幂运算性质（1）am·an=am+n (m、n为整数)
（2）am÷an=am-n (a≠0 ,m、n为整数)
（3）(am)n=amn (m、n为整数)
（4）(ab)n=anbn (n为整数)◆ 指数从正整数推广到了整数，
◆ 正整数指数幂的各种运算法则对整数
指数幂都适用。?例题解析例题解析 【例2】用小数或分数表示下列各数：。。。。。 2. 用小数或整数表示下列各负整数指数幂的值：

计算：(5) (6) 3-3×37计算1、76÷786、（-5）-2×（-5）24、a4÷（a3.a2）2、30×3-25、（-4）8÷4103、25×2-7⑴(-5)5÷(-5)3
(2) (a3)5÷(a2)3
⑶(-ab)3÷(ab)2
⑷ a8÷a4·a4
⑸(-a-b)5÷(a+b)2
⑹y3÷(y-2)3
⑺ 2×2n÷2n-1-( - 3.14)0+2-2拓 展 练 习nn(n为正整数)
2、计算：
（n为正整数）
3、（1）

（2） =1，则 x= ;若
则 ， 3、计算(1)a m+2÷a m+1×a m
(2) (-x)5 ÷x3 ÷(-x)4、已知：am=5,an=4,求a 3m-2n的值。 拓展思维 (1) 已知 2n=8,则4n-1=
(2) a10÷ an= a4 ，则n=
(3) 812-x=27x+4, 则 x=拓 展 练 习
本节课你的收获是什么？小结本节课你学到了什么?nn(a≠0)