人教A版2019选择性必修第一册高二数学课件1.4.1用空间向量研究直线、平面的位置关系(共36张PPT)
文档属性
| 名称 | 人教A版2019选择性必修第一册高二数学课件1.4.1用空间向量研究直线、平面的位置关系(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 15:55:12 | ||
图片预览








文档简介
(共36张PPT)
直线
1.4.1 用空间向量研究直线、平面的位置关系
复习引入
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题.
1.空间中点、直线和平面的向量表示
我们知道,点、直线和平面是空间的基本图形,点、线段和平面图形等是组成空间几何体的基本元素.因此,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、直线和平面.
新知探索
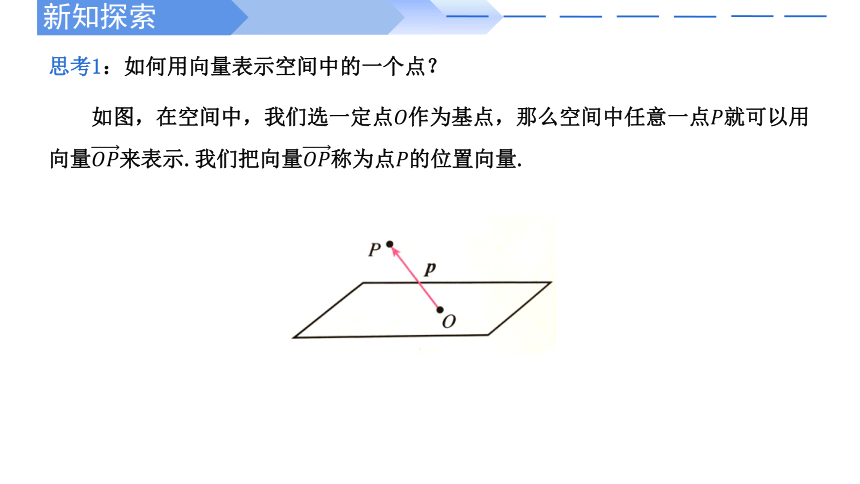
思考1:如何用向量表示空间中的一个点?
如图,在空间中,我们选一定点作为基点,那么空间中任意一点就可以用向量来表示.我们把向量称为点的位置向量.
新知探索
思考2:我们知道,空间中给定一个点和一个方向就能唯一确定一条直线.如何用向量表示直线?
用向量表示直线就是要利用点和直线的方向向量表示直线上的任意一点.
如图,是直线的方向向量,在直线上取,设是直线上的任意一点,由向量共线的条件可知,点在直线上的充要条件是存在实数,使得即
新知探索
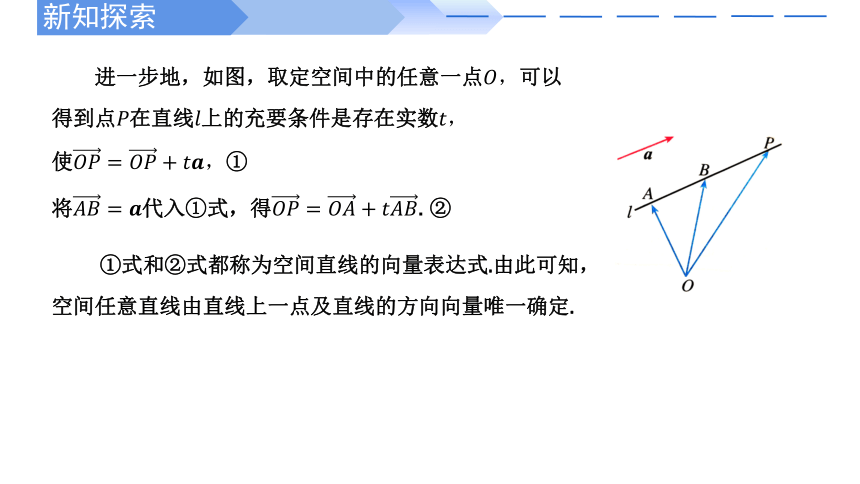
进一步地,如图,取定空间中的任意一点,可以得到点在直线上的充要条件是存在实数,
使,①
将代入①式,得. ②
①式和②式都称为空间直线的向量表达式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
新知探索
思考3:一个定点和两个定方向能否确定一个平面?进一步地,一个定点和一个定方向能否确定一个平面?如果能确定,如何用向量表示这个平面?
我们知道,平面可以由内两条相交直线确定.如图,设两条相交直线交于点,它们的方向向量分别为和为平面内任意一点,由平面向量基本定理可知,存在唯一的有序实数对,使得
具体表示出平面内的任意一点.这种表示在解决几何问题时有重要作用.
新知探索
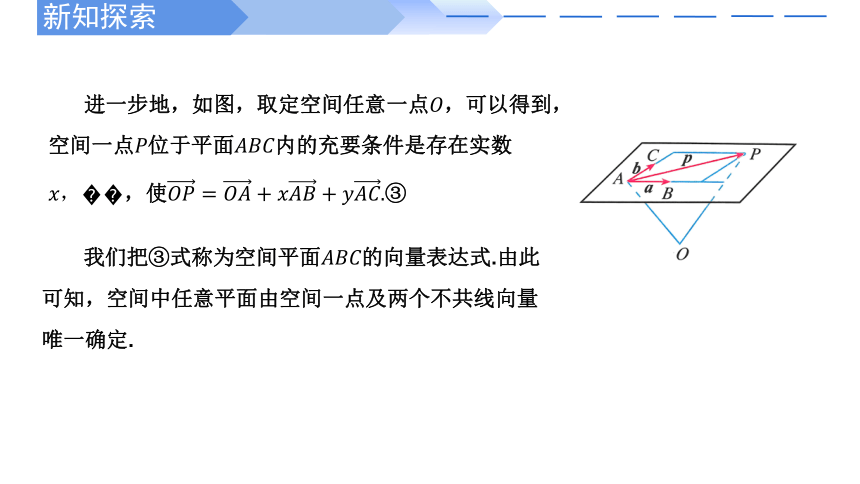
进一步地,如图,取定空间任意一点,可以得到,空间一点位于平面内的充要条件是存在实数,使③
我们把③式称为空间平面的向量表达式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
新知探索
我们知道,给定空间一点和一条直线,则过点且垂直于直线的平面是唯一确定的.由此受到启发,我们可以利用点和直线的方向向量来确定平面.
如图,直线取直线的方向向量,我们称向量为平面的法向量,给定一个点和一个向量,那么过点,且以向量为法向量的平面完全确定,可以表示为集合
例析
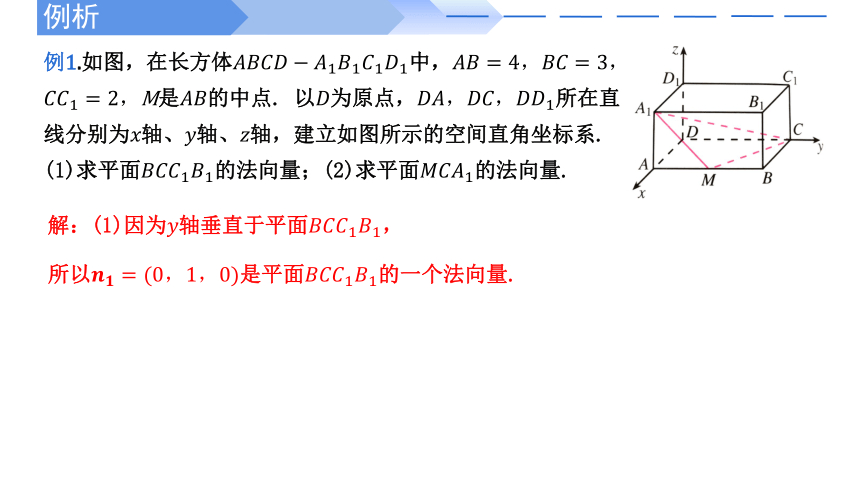
例1.如图,在长方体中,
M是的中点. 以为原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.
(1)求平面的法向量;(2)求平面的法向量.
解:(1)因为轴垂直于平面,
所以是平面的一个法向量.
例析
解:(2)因为M是的中点,所以,的坐标分别为,,.
因此,.
设是平面的法向量,则,.
所以所以
取,则,.于是是平面的一个法向量.
新知探索
思考4:由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系
我们知道,直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量.那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢?首先来看平行的问题.
新知探索
如图,设分别是直线的方向向量.由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行.
所以,使得
新知探索
类似地,如图,设是直线的方向向量,是平面的法向量,则
新知探索
如图,设分别是平面的法向量,则
使得
例析
例2.证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,,,,,.
求证:
证明:如图,取平面的法向量,直线的方向向量,.
因为,,所以.
因为
所以对任意点,存在,使得.
从而.
所以,向量也是平面的法向量.故
例析
例3.如图,在长方体中,.线段上是否存在点,使得平面?
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.因为,,的坐标分别为,,,
所以,.
设是平面的法向量,则,,即所以
例析
例3.如图,在长方体中,.线段上是否存在点,使得平面?
取,则,.所以,是平面的一个法向量.由,,的坐标分别为,,,得,.设点满足则,
所以.
令,得,解得,
此时平面,这样的点存在.所以,当,即为的中点时,平面.
新知探索
思考5:类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间什么关系
一般地,直线与直线垂直,就是两直线的方向向量垂直;如图,设直线
的方向向量分别为,则
新知探索
,使得
直线与平面垂直,就是直线的方向向量与平面的法向量平行;如图,设直线的方向向量分别为,平面的法向量为,则
新知探索
平面与平面垂直,就是两平面的法向量垂直;如图,设平面的法向量分别为则
例析
例4.如图,在平行六面体中,求证:直线平面.
证明:设,,,则为空间的一个基底,
且,,.因为所以
在平面上,取,为基向量,则对于平面上任意一点,
存在唯一的有序实数对,使得
所以,
所以是平面的法向量.所以平面.
例析
例5.证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,,求证:.
证明:取直线的方向向量,平面的法向量.
因为,所以是平面的法向量.
因为,而是平面的法向量,所以.
所以.
练习
题型一:求平面的法向量
例1.已知平面经过三点,,,求平面的一个法向量.
解:∵
∴
设平面的法向量为,则有即
得.
令,则所以平面的一个法向量为.
练习
方法技巧:
利用待定系数法求法向量的步骤
设向量:设平面的法向量为
选向量:在平面内选取不共线向量,
列方程组:由列出等式.解方程组:解由得出的方程组.
赋非零值:取中一个为非零值(常取1).
得结论:得到平面的一个法向量.
练习
变1.已知四边形是直角梯形,,平面,,.在如图所示的坐标系
中,分别求平面和平面的一个法向量.
解:
∵平面,∴是平面的一个法向量.
设平面的法向量为,则,
∴.又,
∴.令,则
∴即为平面的一个法向量.
练习
题型二:利用空间向量证明平行问题
例2.已知正方体的棱长为2,分别是,的中点,求证:平面.
证明:建立如图所示空间直角坐标系,则有
所以,,.
设是平面的法向量,则,,
即得令,则,
所以.因为,所以.
又因为平面,所以平面.
练习
方法技巧:
利用向量法证明平行问题的两种途径
(1)利用三角形法则和平面向量基本定理实现向量间的相互转化,得到向量的共线关系;
(2)通过建立空间直角坐标系,借助直线的方向向量和平面的法向量进行平行关系的证明.
练习
变2.已知正方体的棱长为2,分别是,的中点,求证:平面平面.
证明:建立如图所示空间直角坐标系,则有
所以,设是平面的法向量,则,,
即得令,则,
所以.
因为,所以平面平面.
练习
题型三:利用空间向量证明垂直问题
例3.在四棱锥中,底面是正方形,底面,且是的中点.求证:平面平面.
证明:设,建立如图所示的空间直角坐标系,
设平面的法向量为易知
∴即
令,可得平面的一个法向量为.
∵平面,∴平面的一个法向量为
∵,∴平平面.
练习
方法技巧:
利用向量法证明线、面垂直的策略
(1)用向量法判定线面垂直,只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直.
(2)用向量法判定两个平面垂直,只需求出这两个平面的法向量,再看它们的数量积是否为0即可.
练习
变3.如图,长方体中,点为的中点,求证:直线平面.
证明:依题意,以为坐标原点,建立如图所示的空间直角坐标系,则
于是,,
∴
故,,即,,
又,且平面,平面.
故直线平面.
课堂小结
1.点的位置向量:
在空间中,我们选一定点作为基点,那么空间中任意一点就可以用向量来表示.我们把向量称为点的位置向量.
2.空间直线的向量表示式:
取定空间中的任意一点,可以得到点在直线上的充要条件是存在实数,使,①将代入①式,得. ②
①式和②式都称为空间直线的向量表达式.
课堂小结
3.平面的向量表达式:
取定空间任意一点,可以得到,空间一点位于平面内的充要条件是存在实数,使上式称为空间平面的向量表达式.
4.平面的法向量:
如图,直线取直线的方向向量,我们称向量为平面的法向量,给定一个点和一个向量,那么过点,且以向量为法向量的平面完全确定,可以表示为集合
课堂小结
5.直线与直线平行:
设分别是直线的方向向量,则:
使得
6.直线与平面平行:
设是直线的方向向量,是平面的法向量,则
7.平面与平面平行:
设分别是平面的法向量,则
使得
课堂小结
8.直线与直线垂直:
设直线的方向向量分别为,则
9.直线与平面垂直:
设直线的方向向量分别为,平面的法向量为,则
,使得
10.平面与平面垂直:
设平面的法向量分别为则
作业
(1)整理本节课的题型;
(2)课本P29的练习1、2、3题;
(3)课本P31的练习第3题;
(4)课本P33的练习1、2、3题.
直线
1.4.1 用空间向量研究直线、平面的位置关系
复习引入
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题.
1.空间中点、直线和平面的向量表示
我们知道,点、直线和平面是空间的基本图形,点、线段和平面图形等是组成空间几何体的基本元素.因此,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、直线和平面.
新知探索
思考1:如何用向量表示空间中的一个点?
如图,在空间中,我们选一定点作为基点,那么空间中任意一点就可以用向量来表示.我们把向量称为点的位置向量.
新知探索
思考2:我们知道,空间中给定一个点和一个方向就能唯一确定一条直线.如何用向量表示直线?
用向量表示直线就是要利用点和直线的方向向量表示直线上的任意一点.
如图,是直线的方向向量,在直线上取,设是直线上的任意一点,由向量共线的条件可知,点在直线上的充要条件是存在实数,使得即
新知探索
进一步地,如图,取定空间中的任意一点,可以得到点在直线上的充要条件是存在实数,
使,①
将代入①式,得. ②
①式和②式都称为空间直线的向量表达式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
新知探索
思考3:一个定点和两个定方向能否确定一个平面?进一步地,一个定点和一个定方向能否确定一个平面?如果能确定,如何用向量表示这个平面?
我们知道,平面可以由内两条相交直线确定.如图,设两条相交直线交于点,它们的方向向量分别为和为平面内任意一点,由平面向量基本定理可知,存在唯一的有序实数对,使得
具体表示出平面内的任意一点.这种表示在解决几何问题时有重要作用.
新知探索
进一步地,如图,取定空间任意一点,可以得到,空间一点位于平面内的充要条件是存在实数,使③
我们把③式称为空间平面的向量表达式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
新知探索
我们知道,给定空间一点和一条直线,则过点且垂直于直线的平面是唯一确定的.由此受到启发,我们可以利用点和直线的方向向量来确定平面.
如图,直线取直线的方向向量,我们称向量为平面的法向量,给定一个点和一个向量,那么过点,且以向量为法向量的平面完全确定,可以表示为集合
例析
例1.如图,在长方体中,
M是的中点. 以为原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.
(1)求平面的法向量;(2)求平面的法向量.
解:(1)因为轴垂直于平面,
所以是平面的一个法向量.
例析
解:(2)因为M是的中点,所以,的坐标分别为,,.
因此,.
设是平面的法向量,则,.
所以所以
取,则,.于是是平面的一个法向量.
新知探索
思考4:由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系
我们知道,直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量.那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢?首先来看平行的问题.
新知探索
如图,设分别是直线的方向向量.由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行.
所以,使得
新知探索
类似地,如图,设是直线的方向向量,是平面的法向量,则
新知探索
如图,设分别是平面的法向量,则
使得
例析
例2.证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,,,,,.
求证:
证明:如图,取平面的法向量,直线的方向向量,.
因为,,所以.
因为
所以对任意点,存在,使得.
从而.
所以,向量也是平面的法向量.故
例析
例3.如图,在长方体中,.线段上是否存在点,使得平面?
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系.因为,,的坐标分别为,,,
所以,.
设是平面的法向量,则,,即所以
例析
例3.如图,在长方体中,.线段上是否存在点,使得平面?
取,则,.所以,是平面的一个法向量.由,,的坐标分别为,,,得,.设点满足则,
所以.
令,得,解得,
此时平面,这样的点存在.所以,当,即为的中点时,平面.
新知探索
思考5:类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间什么关系
一般地,直线与直线垂直,就是两直线的方向向量垂直;如图,设直线
的方向向量分别为,则
新知探索
,使得
直线与平面垂直,就是直线的方向向量与平面的法向量平行;如图,设直线的方向向量分别为,平面的法向量为,则
新知探索
平面与平面垂直,就是两平面的法向量垂直;如图,设平面的法向量分别为则
例析
例4.如图,在平行六面体中,求证:直线平面.
证明:设,,,则为空间的一个基底,
且,,.因为所以
在平面上,取,为基向量,则对于平面上任意一点,
存在唯一的有序实数对,使得
所以,
所以是平面的法向量.所以平面.
例析
例5.证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,,求证:.
证明:取直线的方向向量,平面的法向量.
因为,所以是平面的法向量.
因为,而是平面的法向量,所以.
所以.
练习
题型一:求平面的法向量
例1.已知平面经过三点,,,求平面的一个法向量.
解:∵
∴
设平面的法向量为,则有即
得.
令,则所以平面的一个法向量为.
练习
方法技巧:
利用待定系数法求法向量的步骤
设向量:设平面的法向量为
选向量:在平面内选取不共线向量,
列方程组:由列出等式.解方程组:解由得出的方程组.
赋非零值:取中一个为非零值(常取1).
得结论:得到平面的一个法向量.
练习
变1.已知四边形是直角梯形,,平面,,.在如图所示的坐标系
中,分别求平面和平面的一个法向量.
解:
∵平面,∴是平面的一个法向量.
设平面的法向量为,则,
∴.又,
∴.令,则
∴即为平面的一个法向量.
练习
题型二:利用空间向量证明平行问题
例2.已知正方体的棱长为2,分别是,的中点,求证:平面.
证明:建立如图所示空间直角坐标系,则有
所以,,.
设是平面的法向量,则,,
即得令,则,
所以.因为,所以.
又因为平面,所以平面.
练习
方法技巧:
利用向量法证明平行问题的两种途径
(1)利用三角形法则和平面向量基本定理实现向量间的相互转化,得到向量的共线关系;
(2)通过建立空间直角坐标系,借助直线的方向向量和平面的法向量进行平行关系的证明.
练习
变2.已知正方体的棱长为2,分别是,的中点,求证:平面平面.
证明:建立如图所示空间直角坐标系,则有
所以,设是平面的法向量,则,,
即得令,则,
所以.
因为,所以平面平面.
练习
题型三:利用空间向量证明垂直问题
例3.在四棱锥中,底面是正方形,底面,且是的中点.求证:平面平面.
证明:设,建立如图所示的空间直角坐标系,
设平面的法向量为易知
∴即
令,可得平面的一个法向量为.
∵平面,∴平面的一个法向量为
∵,∴平平面.
练习
方法技巧:
利用向量法证明线、面垂直的策略
(1)用向量法判定线面垂直,只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直.
(2)用向量法判定两个平面垂直,只需求出这两个平面的法向量,再看它们的数量积是否为0即可.
练习
变3.如图,长方体中,点为的中点,求证:直线平面.
证明:依题意,以为坐标原点,建立如图所示的空间直角坐标系,则
于是,,
∴
故,,即,,
又,且平面,平面.
故直线平面.
课堂小结
1.点的位置向量:
在空间中,我们选一定点作为基点,那么空间中任意一点就可以用向量来表示.我们把向量称为点的位置向量.
2.空间直线的向量表示式:
取定空间中的任意一点,可以得到点在直线上的充要条件是存在实数,使,①将代入①式,得. ②
①式和②式都称为空间直线的向量表达式.
课堂小结
3.平面的向量表达式:
取定空间任意一点,可以得到,空间一点位于平面内的充要条件是存在实数,使上式称为空间平面的向量表达式.
4.平面的法向量:
如图,直线取直线的方向向量,我们称向量为平面的法向量,给定一个点和一个向量,那么过点,且以向量为法向量的平面完全确定,可以表示为集合
课堂小结
5.直线与直线平行:
设分别是直线的方向向量,则:
使得
6.直线与平面平行:
设是直线的方向向量,是平面的法向量,则
7.平面与平面平行:
设分别是平面的法向量,则
使得
课堂小结
8.直线与直线垂直:
设直线的方向向量分别为,则
9.直线与平面垂直:
设直线的方向向量分别为,平面的法向量为,则
,使得
10.平面与平面垂直:
设平面的法向量分别为则
作业
(1)整理本节课的题型;
(2)课本P29的练习1、2、3题;
(3)课本P31的练习第3题;
(4)课本P33的练习1、2、3题.
