人教A版2019选择性必修第一册高二数学课件1.4.2用空间向量研究距离、夹角问题(第2课时))(共31张PPT)
文档属性
| 名称 | 人教A版2019选择性必修第一册高二数学课件1.4.2用空间向量研究距离、夹角问题(第2课时))(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 15:55:54 | ||
图片预览










文档简介
(共31张PPT)
直线
1.4.2 用空间向量研究距离、夹角问题
(第2课时:用空间向量研究空间角问题)
复习引入
与距离类似,角度是立体几何中另一个重要的度量.下面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角,先看下列问题.
例析
例7.如图,在棱长为1的正四面体(四个面都是正三角形)中分别为的中点,求直线和夹角的余弦值.
解:(化为向量问题)如图,以作为基底,
则.
设向量与的夹角为,则直线和夹角的余弦值等于.
(进行向量运算)
例析
例7.如图,在棱长为1的正四面体(四个面都是正三角形)中分别为的中点,求直线和夹角的余弦值.
解:又和均为等边三角形,所以.
所以
(回到图形问题)
所以直线和夹角的余弦值为
新知探索
思考1:以上我们用向量方法解决了异面直线和所成角的问题,你能用向量方法求直线与平面所成的角吗?
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得.也就是说,若异面直线,所成的角为,其方向向量分别是,则.
新知探索
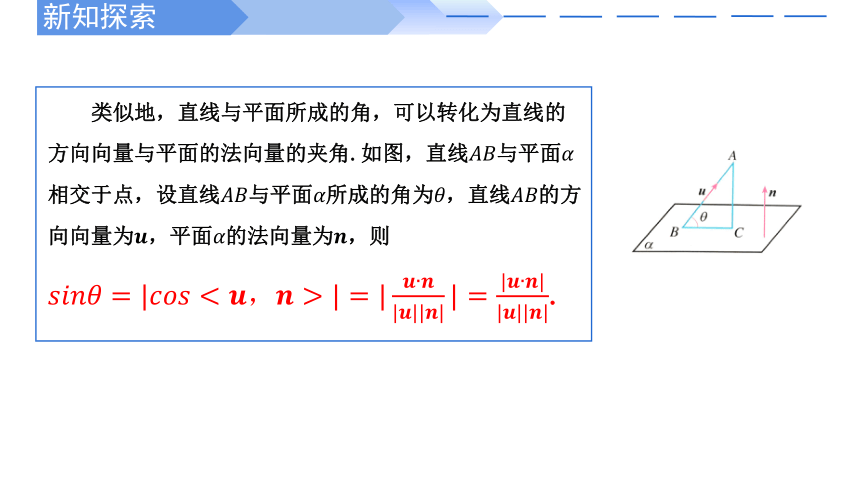
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图,直线与平面相交于点,设直线与平面所成的角为,直线的方向向量为,平面的法向量为,则
.
新知探索
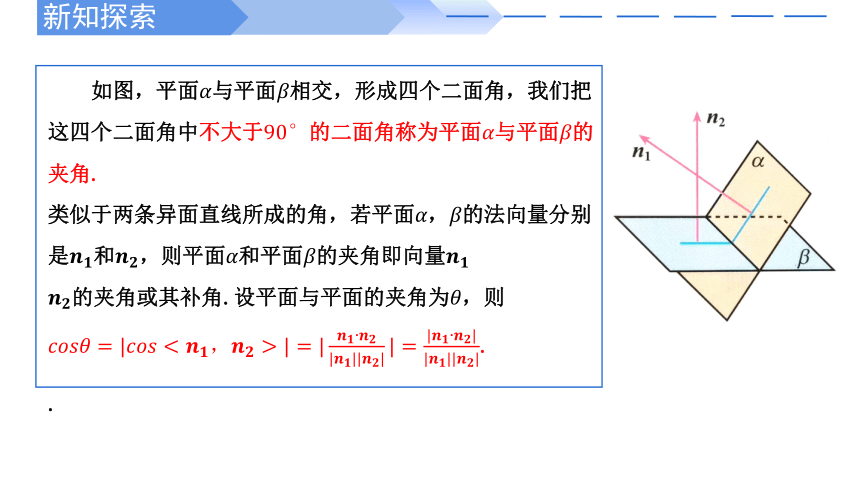
如图,平面与平面相交,形成四个二面角,我们把这四个二面角中不大于的二面角称为平面与平面的夹角.
类似于两条异面直线所成的角,若平面,的法向量分别是和,则平面和平面的夹角即向量
的夹角或其补角.设平面与平面的夹角为,则
.
.
例析
例8.如图,在直三棱柱中,,,,为的中点,点,分别在棱,上,,.求平面与平面夹角的余弦值.
解:(化为向量问题)以为原点,所在直线为轴、轴、轴,建立如图所示的空间直角坐标系.设平面的法向量为,平面的法向量为,则平面与平面的夹角就是与的夹角或其补角.
(进行向量运算)因为平面,所以平面的一个法向量为.
例析
例8.如图,在直三棱柱中,,,,为的中点,点,分别在棱,上,,.求平面与平面夹角的余弦值.
解:根据所建立的空间直角坐标系,可知,,
所以设,则
所以所以取,则
.
例析
例8.如图,在直三棱柱中,,,,为的中点,点,分别在棱,上,,.求平面与平面夹角的余弦值.
解:(回到图形问题)设平面与平面的夹角为,则
即平面与平面的夹角的余弦值为
例析
例9.图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的夹角均为已知礼物的质量为,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度取,精确到).
解:如图,设水平面的单位法向量为,其中一根绳子的拉力为.
因为,所以在上的投影向量为.
所以8根绳子拉力的合力
又因为降落伞匀速下落,所以
所以
所以
例析
例10.如图,在四棱锥中,底面是正方形,侧棱底面,,是的中点,作交于点.
(1)求证:平面;
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,设.
(1)证明:连接,交于点,连接.依题意得.
因为底面是正方形,所以点是它的中心,故点的坐标为,且,.所以,即.
而平面,且平面,因此平面.
例析
例10.如图,在四棱锥中,底面是正方形,侧棱底面,,是的中点,作交于点.
(2)求证:平面;
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,设.
(2)证明:依题意得.
又,故
所以.
由已知,且,所以平面.
例析
(3)求平面与平面的夹角的大小.
解:(3)已知,由(2)可知,故是平面与
平面的夹角.由(2)可知点的坐标为,则.
因为,所以
即.设,
则.所以,点的坐标为.
又点的坐标为,所以.
所以.
所以,即平面与平面的夹角大小为.
例析
通过本节的学习,你对立体几何中的向量法是否有了一定的认识?请结合例题就下面的框图谈谈体会.
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.你能说出它们各自的特点吗?
综合法以逻辑推理作为工具解决问题;向量法利用向量的概念及其运算解决问题,如本节的例7、例9;坐标法利用数及其运算来解决问题,坐标法经常与向量法结合起来使用,如本节的例6,例8,例10.对于具体的问题,应根据它的条件和所求选择合适的方法.
练习
题型一:求异面直线所成角的问题
例1.(2017全国卷Ⅱ)已知直三棱柱中,,,
,则异面直线与所成角的余弦值为( ).
A. B. C. D.
解:如图所示,以为坐标原点,所在的直线为轴,垂直于的直线为轴,所在直线为轴建立空间直角坐标系,由已知条件知
则,.
所以
所以异面直线与所成的角的余弦值为.
练习
方法技巧:
用坐标法求异面直线所成角的一般步骤
(1)建立空间直角坐标系;
(2)分别求出两条异面直线的方向向量的坐标;
(3)利用向量的夹角公式计算两条直线的方向向量的夹角;
(4)结合异面直线所成角的范围求出异面直线所成的角.
练习
变1.如图,在三棱锥中,顶点在空间直角坐标系的原点处,顶点分别在,,轴上,是线段的中点,且,,求异面直线与所成角的余弦值.
解:因为,是的中点,所以,,
,.在中,,,故.
所以
所以.
所以异面直线与所成角的余弦值为.
练习
题型二:求线面角的问题
例2.如图,四边形为正方形,,分别为,的中点,以为折痕把折起,使点到达点的位置,且.
(1)求证:平面平面;
(2)求与平面所成角的正弦值.
(1)证明:由已知可得,,
又所以平面.
又平面,所以平面平面.
(2)如图,作,垂足为.由(1)得,平面.
以为坐标原点,的方向为轴正方向,为单位长,建立如图所示的空间直角坐标系.
练习
(2)求与平面所成角的正弦值.
由(1)可得,.
又因为,所以.
又,,所以.所以,.
则,,,,.
又为平面的一个法向量,设与平面所成角为,
则.
所以与平面所成角的正弦值为.
练习
方法技巧:
利用法向量求直线与平面的夹角的步骤
(1)建立空间直角坐标系;
(2)求直线的方向向量;
(3)求平面的法向量;
(4)计算:设线面角为,则.
练习
变2.如图,在长方体中,,点分别在上,过点的平面与此长方体的底面相交,交线围成一个正方形.
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线与平面所成角的正弦值.
解:(1)交线围成的正方形如图.
(2)作,垂足为,则,.因为四边形为正方形,所以.
于是,所以.
练习
变2.如图,在长方体中,,点分别在上,过点的平面与此长方体的底面相交,交线围成一个正方形.
(2)求直线与平面所成角的正弦值.
解:以为坐标原点,的方向为轴正方向,建立如图所示的空间直角坐标系,则,,,,
,.设是平面的法向量,
则即所以可取.又,故.所以与平面所成角的正弦值为.
练习
题型三:求平面与平面的夹角问题
例3.(2019全国卷Ⅱ)如图,长方体的底面是正方形,点在棱上,.
(1)求证:平面 ;
(2)若求二面角的正弦值.
(1)证:由已知得,平面,平面,
故.又,,所以平面.
(2)由(1)知.由题设知,
所以,故
以为坐标原点,的方向为轴正方向,为单位长度,建立如图所示的空间直角坐标系,
练习
(2)若求二面角的正弦值.
(2)则,,,,,
,.
设平面的法向量为,则即
所以可取.
设平面的法向量为,则即
所以可取
于是.
所以二面角的正弦值为.
练习
方法技巧:
利用向量法求两个平面夹角的步骤
(1)建立空间直角坐标系;
(2)分别求出二面角的两个半平面所在平面的法向量;
(3)求两个法向量的夹角;
(4)确定两平面夹角的大小.
练习
变3.几何体是圆柱的一部分,它是由矩形(及其内部)以边所在直线为旋转轴旋转120得到的,是的中点.
(1)设是上的一点,且,求的大小;
(2)当,时,求平面与平面的夹角的大小.
解:(1)因为,,平面,,
所以平面.又平面,所以.
又,所以.
(2)以为坐标原点,分别以,,所在的直线为轴,轴,
轴,建立如图所示的空间直角坐标系.由题意得,,,,故,,,
练习
(2)当,时,求平面与平面的夹角的大小.
故,,,
设是平面的一个法向量.
由可得取得
设是平面的一个法向量.
由可得取得
所以.
故平面与平面的夹角为60
课堂小结
1.异面直线所成的角:
若异面直线,所成的角为,其方向向量分别是,则
.
2.直线与平面所成的角:
设直线与平面所成的角为,直线的方向向量为,平面的法向量为,则.
课堂小结
3.平面与平面所成的角:
平面与平面相交,形成四个二面角,我们把这四个二面角中不大于的二面角称为平面与平面的夹角.
若平面,的法向量分别是和,则平面和平面的夹角即向量的夹角或其补角.设平面与平面的夹角为,则
.
作业
(1)整理本节课的题型;
(2)课本P38的练习1、3、4题;
(3)课本P41的练习2、3题;
(4)课本P43习题1.4第10、15题.
直线
1.4.2 用空间向量研究距离、夹角问题
(第2课时:用空间向量研究空间角问题)
复习引入
与距离类似,角度是立体几何中另一个重要的度量.下面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角,先看下列问题.
例析
例7.如图,在棱长为1的正四面体(四个面都是正三角形)中分别为的中点,求直线和夹角的余弦值.
解:(化为向量问题)如图,以作为基底,
则.
设向量与的夹角为,则直线和夹角的余弦值等于.
(进行向量运算)
例析
例7.如图,在棱长为1的正四面体(四个面都是正三角形)中分别为的中点,求直线和夹角的余弦值.
解:又和均为等边三角形,所以.
所以
(回到图形问题)
所以直线和夹角的余弦值为
新知探索
思考1:以上我们用向量方法解决了异面直线和所成角的问题,你能用向量方法求直线与平面所成的角吗?
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得.也就是说,若异面直线,所成的角为,其方向向量分别是,则.
新知探索
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图,直线与平面相交于点,设直线与平面所成的角为,直线的方向向量为,平面的法向量为,则
.
新知探索
如图,平面与平面相交,形成四个二面角,我们把这四个二面角中不大于的二面角称为平面与平面的夹角.
类似于两条异面直线所成的角,若平面,的法向量分别是和,则平面和平面的夹角即向量
的夹角或其补角.设平面与平面的夹角为,则
.
.
例析
例8.如图,在直三棱柱中,,,,为的中点,点,分别在棱,上,,.求平面与平面夹角的余弦值.
解:(化为向量问题)以为原点,所在直线为轴、轴、轴,建立如图所示的空间直角坐标系.设平面的法向量为,平面的法向量为,则平面与平面的夹角就是与的夹角或其补角.
(进行向量运算)因为平面,所以平面的一个法向量为.
例析
例8.如图,在直三棱柱中,,,,为的中点,点,分别在棱,上,,.求平面与平面夹角的余弦值.
解:根据所建立的空间直角坐标系,可知,,
所以设,则
所以所以取,则
.
例析
例8.如图,在直三棱柱中,,,,为的中点,点,分别在棱,上,,.求平面与平面夹角的余弦值.
解:(回到图形问题)设平面与平面的夹角为,则
即平面与平面的夹角的余弦值为
例析
例9.图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的夹角均为已知礼物的质量为,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度取,精确到).
解:如图,设水平面的单位法向量为,其中一根绳子的拉力为.
因为,所以在上的投影向量为.
所以8根绳子拉力的合力
又因为降落伞匀速下落,所以
所以
所以
例析
例10.如图,在四棱锥中,底面是正方形,侧棱底面,,是的中点,作交于点.
(1)求证:平面;
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,设.
(1)证明:连接,交于点,连接.依题意得.
因为底面是正方形,所以点是它的中心,故点的坐标为,且,.所以,即.
而平面,且平面,因此平面.
例析
例10.如图,在四棱锥中,底面是正方形,侧棱底面,,是的中点,作交于点.
(2)求证:平面;
解:以为原点,,,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,设.
(2)证明:依题意得.
又,故
所以.
由已知,且,所以平面.
例析
(3)求平面与平面的夹角的大小.
解:(3)已知,由(2)可知,故是平面与
平面的夹角.由(2)可知点的坐标为,则.
因为,所以
即.设,
则.所以,点的坐标为.
又点的坐标为,所以.
所以.
所以,即平面与平面的夹角大小为.
例析
通过本节的学习,你对立体几何中的向量法是否有了一定的认识?请结合例题就下面的框图谈谈体会.
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.你能说出它们各自的特点吗?
综合法以逻辑推理作为工具解决问题;向量法利用向量的概念及其运算解决问题,如本节的例7、例9;坐标法利用数及其运算来解决问题,坐标法经常与向量法结合起来使用,如本节的例6,例8,例10.对于具体的问题,应根据它的条件和所求选择合适的方法.
练习
题型一:求异面直线所成角的问题
例1.(2017全国卷Ⅱ)已知直三棱柱中,,,
,则异面直线与所成角的余弦值为( ).
A. B. C. D.
解:如图所示,以为坐标原点,所在的直线为轴,垂直于的直线为轴,所在直线为轴建立空间直角坐标系,由已知条件知
则,.
所以
所以异面直线与所成的角的余弦值为.
练习
方法技巧:
用坐标法求异面直线所成角的一般步骤
(1)建立空间直角坐标系;
(2)分别求出两条异面直线的方向向量的坐标;
(3)利用向量的夹角公式计算两条直线的方向向量的夹角;
(4)结合异面直线所成角的范围求出异面直线所成的角.
练习
变1.如图,在三棱锥中,顶点在空间直角坐标系的原点处,顶点分别在,,轴上,是线段的中点,且,,求异面直线与所成角的余弦值.
解:因为,是的中点,所以,,
,.在中,,,故.
所以
所以.
所以异面直线与所成角的余弦值为.
练习
题型二:求线面角的问题
例2.如图,四边形为正方形,,分别为,的中点,以为折痕把折起,使点到达点的位置,且.
(1)求证:平面平面;
(2)求与平面所成角的正弦值.
(1)证明:由已知可得,,
又所以平面.
又平面,所以平面平面.
(2)如图,作,垂足为.由(1)得,平面.
以为坐标原点,的方向为轴正方向,为单位长,建立如图所示的空间直角坐标系.
练习
(2)求与平面所成角的正弦值.
由(1)可得,.
又因为,所以.
又,,所以.所以,.
则,,,,.
又为平面的一个法向量,设与平面所成角为,
则.
所以与平面所成角的正弦值为.
练习
方法技巧:
利用法向量求直线与平面的夹角的步骤
(1)建立空间直角坐标系;
(2)求直线的方向向量;
(3)求平面的法向量;
(4)计算:设线面角为,则.
练习
变2.如图,在长方体中,,点分别在上,过点的平面与此长方体的底面相交,交线围成一个正方形.
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线与平面所成角的正弦值.
解:(1)交线围成的正方形如图.
(2)作,垂足为,则,.因为四边形为正方形,所以.
于是,所以.
练习
变2.如图,在长方体中,,点分别在上,过点的平面与此长方体的底面相交,交线围成一个正方形.
(2)求直线与平面所成角的正弦值.
解:以为坐标原点,的方向为轴正方向,建立如图所示的空间直角坐标系,则,,,,
,.设是平面的法向量,
则即所以可取.又,故.所以与平面所成角的正弦值为.
练习
题型三:求平面与平面的夹角问题
例3.(2019全国卷Ⅱ)如图,长方体的底面是正方形,点在棱上,.
(1)求证:平面 ;
(2)若求二面角的正弦值.
(1)证:由已知得,平面,平面,
故.又,,所以平面.
(2)由(1)知.由题设知,
所以,故
以为坐标原点,的方向为轴正方向,为单位长度,建立如图所示的空间直角坐标系,
练习
(2)若求二面角的正弦值.
(2)则,,,,,
,.
设平面的法向量为,则即
所以可取.
设平面的法向量为,则即
所以可取
于是.
所以二面角的正弦值为.
练习
方法技巧:
利用向量法求两个平面夹角的步骤
(1)建立空间直角坐标系;
(2)分别求出二面角的两个半平面所在平面的法向量;
(3)求两个法向量的夹角;
(4)确定两平面夹角的大小.
练习
变3.几何体是圆柱的一部分,它是由矩形(及其内部)以边所在直线为旋转轴旋转120得到的,是的中点.
(1)设是上的一点,且,求的大小;
(2)当,时,求平面与平面的夹角的大小.
解:(1)因为,,平面,,
所以平面.又平面,所以.
又,所以.
(2)以为坐标原点,分别以,,所在的直线为轴,轴,
轴,建立如图所示的空间直角坐标系.由题意得,,,,故,,,
练习
(2)当,时,求平面与平面的夹角的大小.
故,,,
设是平面的一个法向量.
由可得取得
设是平面的一个法向量.
由可得取得
所以.
故平面与平面的夹角为60
课堂小结
1.异面直线所成的角:
若异面直线,所成的角为,其方向向量分别是,则
.
2.直线与平面所成的角:
设直线与平面所成的角为,直线的方向向量为,平面的法向量为,则.
课堂小结
3.平面与平面所成的角:
平面与平面相交,形成四个二面角,我们把这四个二面角中不大于的二面角称为平面与平面的夹角.
若平面,的法向量分别是和,则平面和平面的夹角即向量的夹角或其补角.设平面与平面的夹角为,则
.
作业
(1)整理本节课的题型;
(2)课本P38的练习1、3、4题;
(3)课本P41的练习2、3题;
(4)课本P43习题1.4第10、15题.
