物理人教版(2019)选择性必修第三册2.2气体的等温变化(共35张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第三册2.2气体的等温变化(共35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-24 22:24:48 | ||
图片预览







文档简介
(共35张PPT)
§2.2 气体的等温变化
p
V
T2
T1
0
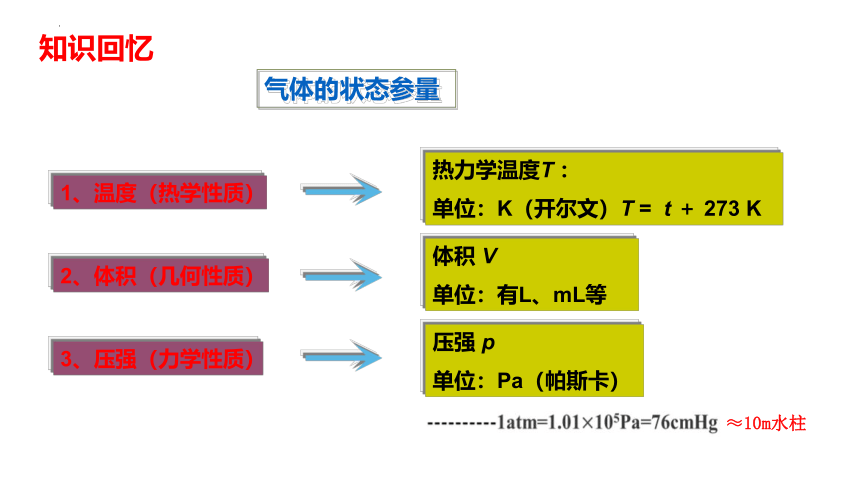
1、温度(热学性质)
2、体积(几何性质)
3、压强(力学性质)
热力学温度T :
单位:K(开尔文)T = t + 273 K
体积 V
单位:有L、mL等
压强 p
单位:Pa(帕斯卡)
气体的状态参量
知识回忆
≈10m水柱
问题
引入新课
在庆典活动中放飞的气球,会飞到我们看不见的地方。随着气球的升空,大气压在减小,温度在降低,气球在膨胀……看来,一定质量的气体的压强、体积和温度三个状态参量之间是有联系的。那么,它们会有怎样的联系呢?
探究方法
控制变量法:
在实验中研究三个物理量的关系时,先保持一个量不变,研究另外两个量的关系;然后再保持另一个量不变,研究剩余两个量的关系,最后把研究结果结合起来,这种方法叫做控制变量法
今天,我们开始来研究气体的三个状态参量T、V、p之间的关系。
首先,我们来研究:当温度( T )保持不变时,体积( V )和压强( p )之间的关系。
猜想
一、等温变化:
一定质量的气体,在温度不变的条件下其压强与体积变化的关系,叫做气体的等温变化。
注射器内一定质量的气体.
气体的压强和体积
变化过程十分缓慢
容器透热
环境恒温
探究:气体的等温变化
1、研究对象是什么?
2、需要测量的物理量有哪些?
3、怎样保证实验过程温度不变?
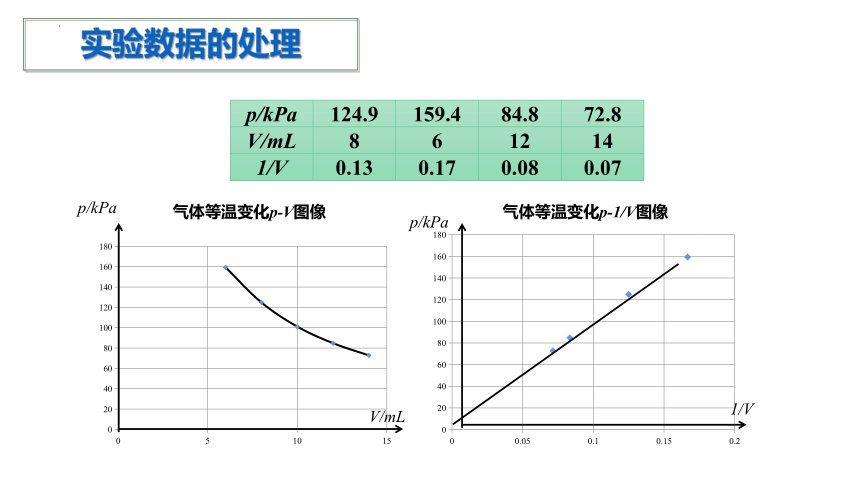
实验数据的处理
p/kPa 124.9 159.4 84.8 72.8
V/mL 8 6 12 14
1/V 0.13 0.17 0.08 0.07
p/kPa
V/mL
p/kPa
1/V
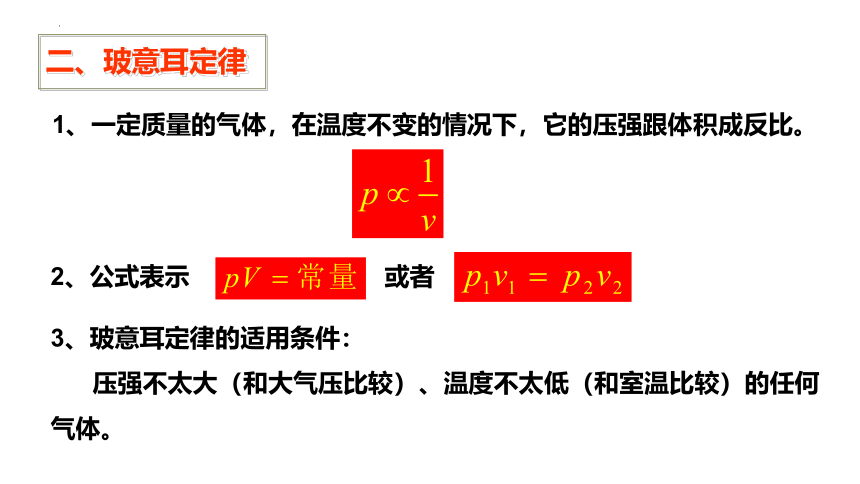
1、一定质量的气体,在温度不变的情况下,它的压强跟体积成反比。
或者
3、玻意耳定律的适用条件:
压强不太大(和大气压比较)、温度不太低(和室温比较)的任何气体。
2、公式表示
二、玻意耳定律
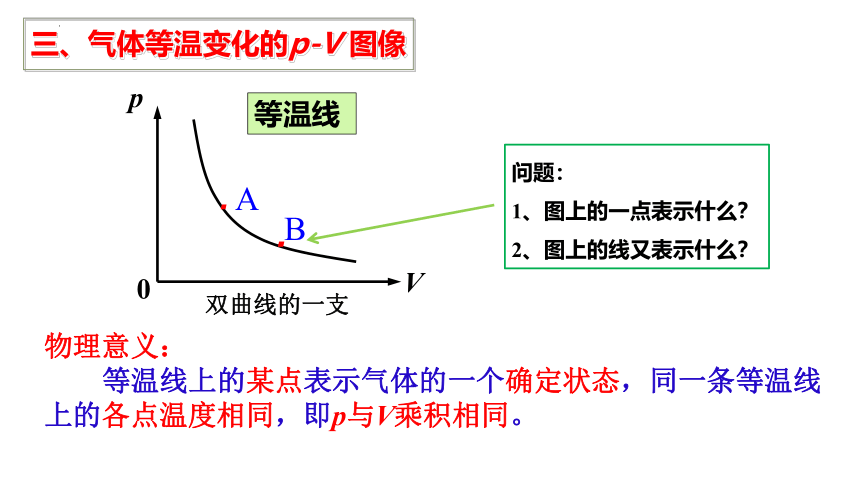
双曲线的一支
物理意义:
等温线上的某点表示气体的一个确定状态,同一条等温线上的各点温度相同,即p与V乘积相同。
V
p
·
0
A
·
B
问题:
1、图上的一点表示什么?
2、图上的线又表示什么?
等温线
三、气体等温变化的p-V 图像
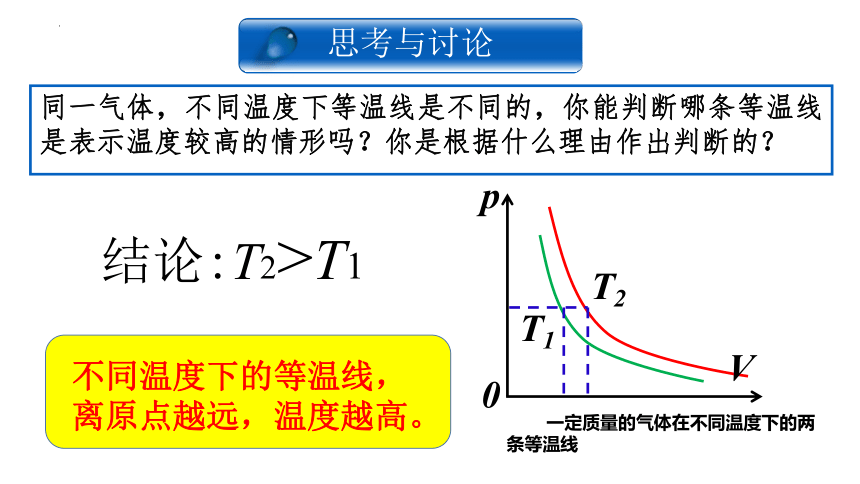
同一气体,不同温度下等温线是不同的,你能判断哪条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?
p
V
T2
T1
一定质量的气体在不同温度下的两条等温线
0
结论:T2>T1
不同温度下的等温线,离原点越远,温度越高。
思考与讨论
『判一判』
(1)玻意耳定律是英国科学家玻意耳和法国科学家马略特各自通过实验发现的。 ( )
(2)公式pV=C中的C是常量,指当p、V变化时C的值不变。 ( )
(3)对于温度不同、质量不同、种类不同的气体,C值是相同的。 ( )
(4)在探究气体的等温变化实验中空气柱体积变化快慢对实验没有影响。
( )
(5)气体等温变化的p-V图象是一条倾斜的直线。 ( )
(6)一定质量的某种气体,在温度保持不变的情况下,压强p与体积V成正比。 ( )
√
×
×
×
×
×
做一做
用传感器探究气体等温变化的规律
1.一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。
答案:1.25×10 5Pa
例题
2.某个容器的容积是10L,所装气体的压强是2×106Pa如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1×105Pa.
例题
设容器原装气体为研究对象。
末态
根据波意耳定律
解得
剩下的气体为原来的
分析:
可认为气体膨胀过程等温变化,
初态
利用玻意耳定律解题的基本思路
(1)明确研究对象;
(2)分析过程特点,判断为等温过程;
(3)列出初、末状态的p、V值;
(4)根据p1V1=p2V2列式求解;
(5)讨论结果。
『想一想』
借助铅笔,把气球塞进一只瓶子里,并拉出气球的吹气口,反扣在瓶口上,如图所示,然后给气球吹气,无论怎么吹,气球不过大了一点,想把气球吹大,非常困难,为什么?
答案:由题意“吹气口反扣在瓶口上”可知瓶内封闭着一定质量的空气。当气球稍吹大时,瓶内空气的体积缩小,根据气体压强、体积的关系,空气的压强增大,阻碍了气球的膨胀,因而再要吹大气球是很困难的。
在一个恒温池中,一串串气泡由池底慢慢升到水面,有趣的是气泡在上升过程中,体积逐渐变大,到水面时就会破裂。请思考:
(1)上升过程中,气泡内气体的温度发生改变吗?
(2)上升过程中,气泡内气体的压强怎么改变?
(3)气泡在上升过程中体积为何会变大?
提示:
(1)因为在恒温池中,所以气泡内气体的温度保持不变。
(2)变小。
(3)由玻意耳定律pV=C可知,压强变小,气体的体积增大。
小试牛刀
1.如图所示是一定质量的某种气体状态变化的p-V图象,气体由状态A变化到状态B的过程中,气体分子平均速率的变化情况是( )
A.一直保持不变
B.一直增大
C.先减小后增大
D.先增大后减小
D
C
2.一支两端开口的细玻璃管,竖直插入水银槽中,水银中部分长为L。然后把上口堵住,缓缓向上提起玻璃管,并最后离开水银槽。则( )
A. 管中水银柱长度仍为L
B. 管中水银全部流出
C. 管中水银柱长小于L
D. 管中水银柱长大于L
C
小试牛刀
小试牛刀
3.某个容器的容积是10L,所装气体的压强是20×105Pa。如果温度保持不变,把容器的开关打开以后,经过足够长时间,容器里剩下的气体是原来的百分之几?设大气压是1.0×105Pa.
解析:
初态 p1=20×105Pa V1=10L T1=T
剩下的气体为原来的
末态 p2=1.0×105Pa V2=?L T2=T
由玻意耳定律 p1V1=p2V2得 V2=200L
小试牛刀
4、(多选)关于“探究气体等温变化的规律”实验,下列说法正确的是 ( )
A.实验过程中应保持被封闭气体的质量和温度不发生变化
B.实验中为找到体积与压强的关系,一定要测量空气柱的横截面积
C.为了减小实验误差,可以在柱塞上涂润滑油,以减小摩擦
D.处理数据时采用 图像,是因为 图像比p-V图像更直观
AD
小试牛刀
以气泡中的气体为研究对象,假设气泡在水底的体积为V0
初状态:
P1=P0+ρgh
V1=V0
末状态:
P2=P0=1.0×105Pa
V2=3V0
由玻意耳定律得 p1V1=p2V2
代入数据解得:h=20m
5.一个气泡从水底升到水面上时,它的体积增大2倍,设水的密度为ρ=1×103kg/m3,大气压强p0=1.0×105Pa,水底与水面温差不计,求水的深度。(g=10m/s2)
解析:
6.装有水银的、两端封闭的U形管,竖直放置时,两侧的水银面一样高。将U形管在所在的竖直平面内向右倾斜时,两侧液面是( )
A.假使液面上方充有空气,一样高
B.假使液面上方充有空气,左侧高
C.假使液面上方充有空气,右侧高
D.假使液面上方是真空的,一样高
BD
小试牛刀
课 堂 小 结
知识与技能
一种方法:
控制变量法
一个规律:
玻意耳定律
过程与方法
通过猜想
设计实验
分析
总结,体会实验探究的过程,掌握实验探究的方法
情感 态度与价值观
在探究的过程中培养合作精神和严谨认真的科学态度。
研究气体等温变化的规律
明确研究对象:
被封闭的气体
注意事项:
防漏气、保温
对甲图,管内空气压强
体积
对乙图,管内空气压强
体积
2、如何确定气体的状态参量呢?
温度( T )、体积( V )和压强( p )
1、描述气体的状态参量有哪些?
温度( T )----------温度计
体积( V )----------容器的容积
压强( p )-----------气压计
知识回忆
实验数据的处理
次数 1 2 3 4 5
压强(×105Pa) 3.0 2.5 2.0 1.5 1.0
体积(L) 1.3 1.6 2.0 2.7 4.0
p /10 Pa
5
V /L
1
2
3
0
1
2
3
4
实验数据的处理
p/10 Pa
5
1/V (1/L)
1
2
3
0
0.2
0.4
0.6
0.8
实验数据的处理
二、探究结论:
在温度不变时,压强p和体积V成反比。
三、玻意耳定律
一定质量的理想气体,在温度保持不变的情况下,压强p与V成反比,或压强P与体积V的乘积保持不变,即:PV=常量
气体作等温变化时,p-V图象形状为双曲线,它描述的是等温变化,所以也称为等温线
在坐标轴中的两条等温线表示的温度t1、t2哪个大?
气体等温变化的p-v图像
§2.2 气体的等温变化
p
V
T2
T1
0
1、温度(热学性质)
2、体积(几何性质)
3、压强(力学性质)
热力学温度T :
单位:K(开尔文)T = t + 273 K
体积 V
单位:有L、mL等
压强 p
单位:Pa(帕斯卡)
气体的状态参量
知识回忆
≈10m水柱
问题
引入新课
在庆典活动中放飞的气球,会飞到我们看不见的地方。随着气球的升空,大气压在减小,温度在降低,气球在膨胀……看来,一定质量的气体的压强、体积和温度三个状态参量之间是有联系的。那么,它们会有怎样的联系呢?
探究方法
控制变量法:
在实验中研究三个物理量的关系时,先保持一个量不变,研究另外两个量的关系;然后再保持另一个量不变,研究剩余两个量的关系,最后把研究结果结合起来,这种方法叫做控制变量法
今天,我们开始来研究气体的三个状态参量T、V、p之间的关系。
首先,我们来研究:当温度( T )保持不变时,体积( V )和压强( p )之间的关系。
猜想
一、等温变化:
一定质量的气体,在温度不变的条件下其压强与体积变化的关系,叫做气体的等温变化。
注射器内一定质量的气体.
气体的压强和体积
变化过程十分缓慢
容器透热
环境恒温
探究:气体的等温变化
1、研究对象是什么?
2、需要测量的物理量有哪些?
3、怎样保证实验过程温度不变?
实验数据的处理
p/kPa 124.9 159.4 84.8 72.8
V/mL 8 6 12 14
1/V 0.13 0.17 0.08 0.07
p/kPa
V/mL
p/kPa
1/V
1、一定质量的气体,在温度不变的情况下,它的压强跟体积成反比。
或者
3、玻意耳定律的适用条件:
压强不太大(和大气压比较)、温度不太低(和室温比较)的任何气体。
2、公式表示
二、玻意耳定律
双曲线的一支
物理意义:
等温线上的某点表示气体的一个确定状态,同一条等温线上的各点温度相同,即p与V乘积相同。
V
p
·
0
A
·
B
问题:
1、图上的一点表示什么?
2、图上的线又表示什么?
等温线
三、气体等温变化的p-V 图像
同一气体,不同温度下等温线是不同的,你能判断哪条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?
p
V
T2
T1
一定质量的气体在不同温度下的两条等温线
0
结论:T2>T1
不同温度下的等温线,离原点越远,温度越高。
思考与讨论
『判一判』
(1)玻意耳定律是英国科学家玻意耳和法国科学家马略特各自通过实验发现的。 ( )
(2)公式pV=C中的C是常量,指当p、V变化时C的值不变。 ( )
(3)对于温度不同、质量不同、种类不同的气体,C值是相同的。 ( )
(4)在探究气体的等温变化实验中空气柱体积变化快慢对实验没有影响。
( )
(5)气体等温变化的p-V图象是一条倾斜的直线。 ( )
(6)一定质量的某种气体,在温度保持不变的情况下,压强p与体积V成正比。 ( )
√
×
×
×
×
×
做一做
用传感器探究气体等温变化的规律
1.一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。
答案:1.25×10 5Pa
例题
2.某个容器的容积是10L,所装气体的压强是2×106Pa如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1×105Pa.
例题
设容器原装气体为研究对象。
末态
根据波意耳定律
解得
剩下的气体为原来的
分析:
可认为气体膨胀过程等温变化,
初态
利用玻意耳定律解题的基本思路
(1)明确研究对象;
(2)分析过程特点,判断为等温过程;
(3)列出初、末状态的p、V值;
(4)根据p1V1=p2V2列式求解;
(5)讨论结果。
『想一想』
借助铅笔,把气球塞进一只瓶子里,并拉出气球的吹气口,反扣在瓶口上,如图所示,然后给气球吹气,无论怎么吹,气球不过大了一点,想把气球吹大,非常困难,为什么?
答案:由题意“吹气口反扣在瓶口上”可知瓶内封闭着一定质量的空气。当气球稍吹大时,瓶内空气的体积缩小,根据气体压强、体积的关系,空气的压强增大,阻碍了气球的膨胀,因而再要吹大气球是很困难的。
在一个恒温池中,一串串气泡由池底慢慢升到水面,有趣的是气泡在上升过程中,体积逐渐变大,到水面时就会破裂。请思考:
(1)上升过程中,气泡内气体的温度发生改变吗?
(2)上升过程中,气泡内气体的压强怎么改变?
(3)气泡在上升过程中体积为何会变大?
提示:
(1)因为在恒温池中,所以气泡内气体的温度保持不变。
(2)变小。
(3)由玻意耳定律pV=C可知,压强变小,气体的体积增大。
小试牛刀
1.如图所示是一定质量的某种气体状态变化的p-V图象,气体由状态A变化到状态B的过程中,气体分子平均速率的变化情况是( )
A.一直保持不变
B.一直增大
C.先减小后增大
D.先增大后减小
D
C
2.一支两端开口的细玻璃管,竖直插入水银槽中,水银中部分长为L。然后把上口堵住,缓缓向上提起玻璃管,并最后离开水银槽。则( )
A. 管中水银柱长度仍为L
B. 管中水银全部流出
C. 管中水银柱长小于L
D. 管中水银柱长大于L
C
小试牛刀
小试牛刀
3.某个容器的容积是10L,所装气体的压强是20×105Pa。如果温度保持不变,把容器的开关打开以后,经过足够长时间,容器里剩下的气体是原来的百分之几?设大气压是1.0×105Pa.
解析:
初态 p1=20×105Pa V1=10L T1=T
剩下的气体为原来的
末态 p2=1.0×105Pa V2=?L T2=T
由玻意耳定律 p1V1=p2V2得 V2=200L
小试牛刀
4、(多选)关于“探究气体等温变化的规律”实验,下列说法正确的是 ( )
A.实验过程中应保持被封闭气体的质量和温度不发生变化
B.实验中为找到体积与压强的关系,一定要测量空气柱的横截面积
C.为了减小实验误差,可以在柱塞上涂润滑油,以减小摩擦
D.处理数据时采用 图像,是因为 图像比p-V图像更直观
AD
小试牛刀
以气泡中的气体为研究对象,假设气泡在水底的体积为V0
初状态:
P1=P0+ρgh
V1=V0
末状态:
P2=P0=1.0×105Pa
V2=3V0
由玻意耳定律得 p1V1=p2V2
代入数据解得:h=20m
5.一个气泡从水底升到水面上时,它的体积增大2倍,设水的密度为ρ=1×103kg/m3,大气压强p0=1.0×105Pa,水底与水面温差不计,求水的深度。(g=10m/s2)
解析:
6.装有水银的、两端封闭的U形管,竖直放置时,两侧的水银面一样高。将U形管在所在的竖直平面内向右倾斜时,两侧液面是( )
A.假使液面上方充有空气,一样高
B.假使液面上方充有空气,左侧高
C.假使液面上方充有空气,右侧高
D.假使液面上方是真空的,一样高
BD
小试牛刀
课 堂 小 结
知识与技能
一种方法:
控制变量法
一个规律:
玻意耳定律
过程与方法
通过猜想
设计实验
分析
总结,体会实验探究的过程,掌握实验探究的方法
情感 态度与价值观
在探究的过程中培养合作精神和严谨认真的科学态度。
研究气体等温变化的规律
明确研究对象:
被封闭的气体
注意事项:
防漏气、保温
对甲图,管内空气压强
体积
对乙图,管内空气压强
体积
2、如何确定气体的状态参量呢?
温度( T )、体积( V )和压强( p )
1、描述气体的状态参量有哪些?
温度( T )----------温度计
体积( V )----------容器的容积
压强( p )-----------气压计
知识回忆
实验数据的处理
次数 1 2 3 4 5
压强(×105Pa) 3.0 2.5 2.0 1.5 1.0
体积(L) 1.3 1.6 2.0 2.7 4.0
p /10 Pa
5
V /L
1
2
3
0
1
2
3
4
实验数据的处理
p/10 Pa
5
1/V (1/L)
1
2
3
0
0.2
0.4
0.6
0.8
实验数据的处理
二、探究结论:
在温度不变时,压强p和体积V成反比。
三、玻意耳定律
一定质量的理想气体,在温度保持不变的情况下,压强p与V成反比,或压强P与体积V的乘积保持不变,即:PV=常量
气体作等温变化时,p-V图象形状为双曲线,它描述的是等温变化,所以也称为等温线
在坐标轴中的两条等温线表示的温度t1、t2哪个大?
气体等温变化的p-v图像
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
