二次函数解析式确定1
图片预览


文档简介
课件15张PPT。义务教育课程标准实验教科书
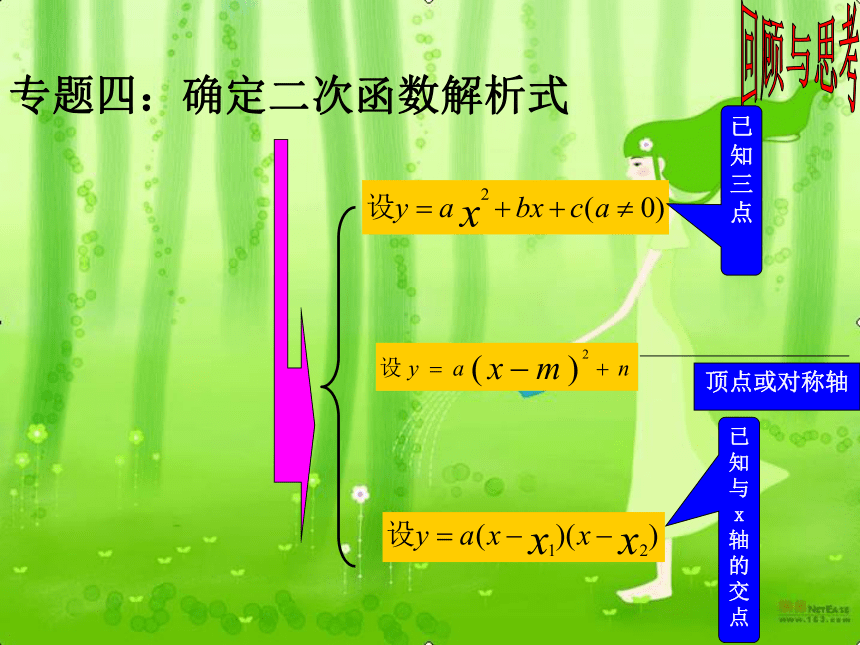
数学 九年级 (上册) QQ:315743419 二次函数辅导 (四)专题四:确定二次函数解析式回顾与思考顶点或对称轴已
知
三
点已
知
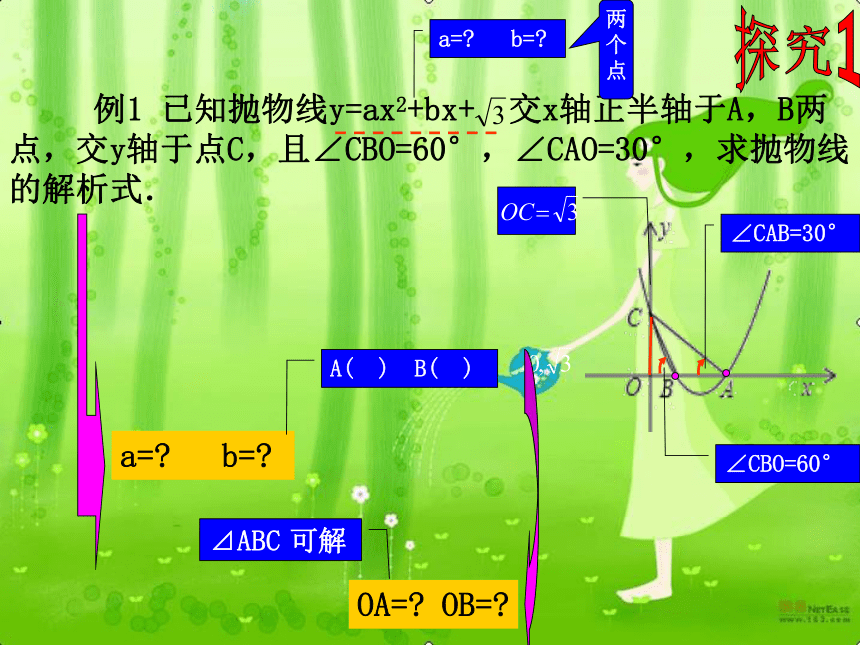
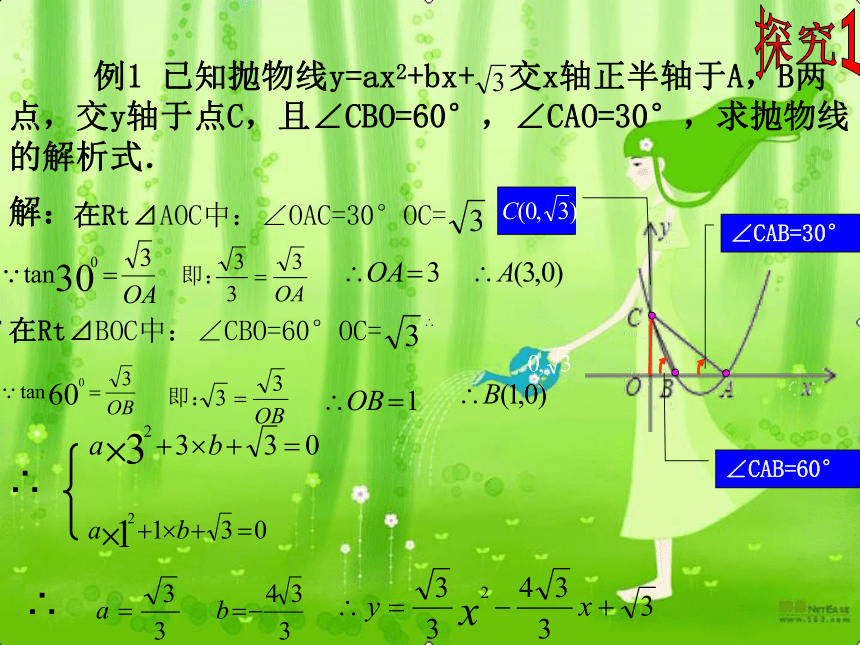
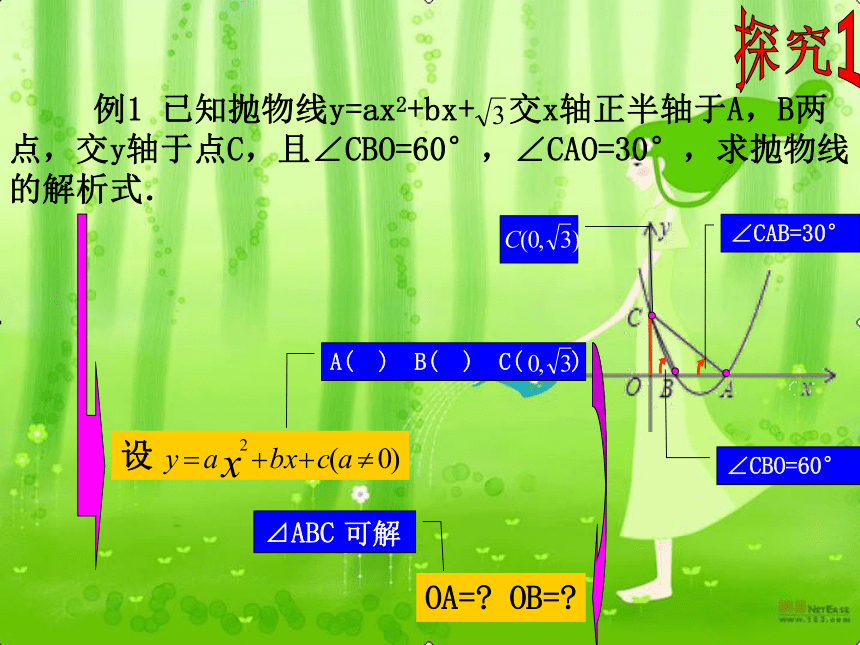
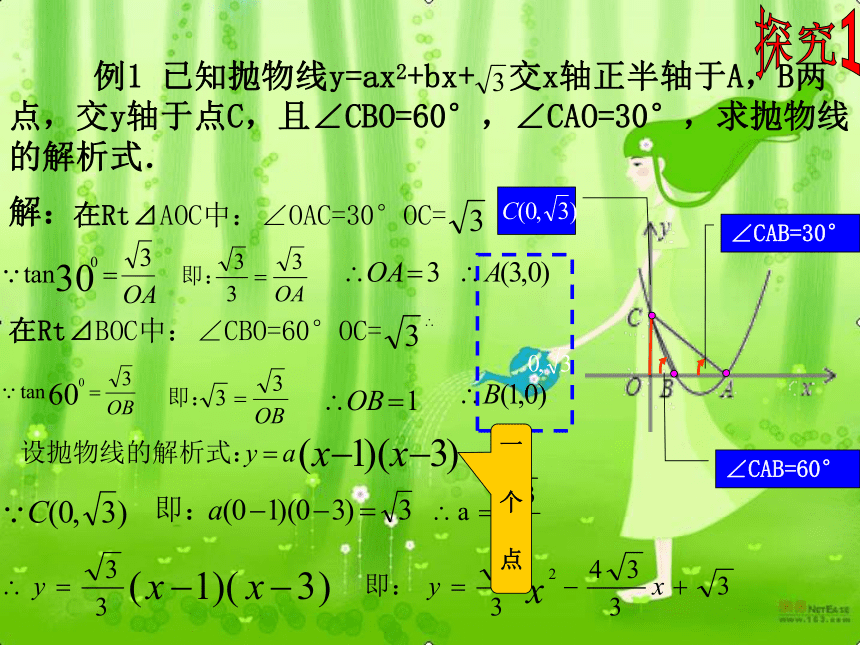
与x轴的交点 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CBO=60°∠CAB=30°a=? b=?A( ) B( )OA=? OB=?⊿ABCa=? b=?两个点可解 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CAB=60°∠CAB=30°解:在Rt⊿AOC中:∠OAC=30°OC=在Rt⊿BOC中:∠CBO=60°OC=∴∴ 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CBO=60°∠CAB=30°设A( ) B( ) C( )OA=? OB=?⊿ABC可解 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式. 探究1∠CAB=60°∠CAB=45°解:在Rt⊿AOC中:∠OAC=30°OC=在Rt⊿BOC中:∠CBO=60°OC=∴∴ 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CAB=60°∠CAB=30°解:在Rt⊿AOC中:∠OAC=30°OC=在Rt⊿BOC中:∠CBO=60°OC=一
个
点探究2 例2 二次函数 的图象与x轴交于A、
B,与y轴交于点C,A、C的坐标分别是(1,0和(0,2),
B在A的右侧,且∠OCA=∠OBC.求这个二次函数的解析式.(1,0)(0,2)⊿AOC∽⊿COB设A( ) B( ) C( )1,00,2OB=?比例式法解直角三角形(1,0)(0,2)解:∴∴∵ ∠OCA=∠OBC, ∠AOC=∠BOC=Rt∠∴⊿ AOC ∽ ⊿ COB∵ A(1,0) C(0,2)∴ OA=1 OC=2(1,0)(0,2)解:∵ ∠OCA=∠OBC, ∠AOC=∠BOC=Rt∠∴⊿ AOC ∽ ⊿ COB∵ A(1,0) C(0,2)∴ OA=1 OC=2(4,0)一
个
点 例3 二次函数图象过A、C、B三点,点A的坐标为(-1,0,点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.求抛物线的解析式探究3(-1,0)(4,0)C(0,5)设a=?一个点( ) 例3 二次函数图象过A、C、B三点,点A的坐标为(-1,0,点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.求抛物线的解析式探究3(-1,0)(4,0)C(4,0)解:∵A(-1,0) B(4,0)∵AB=OC 例4 如图所示,现将一块等腰直角三角板ABC放在第一象
限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),
抛物线y=ax2+ax-2经过点B.求抛物线的解析式.探究4OA=2OC=1 a=?一个点( )点B( , )相关线段的长度DOD=? BD=?∟⊿ ∽ ⊿≌⊿AOC ≌⊿CDBOD=3BD=OC=1B(3,1)探究4OA=2OC=1D解:过点B作BD⊥x轴,垂足为D∵∠ACB=Rt∠∴∠ACO=∠CBD∵AC=BC ∠A0C=∠CDB ∠ACO=∠CBD ∴⊿ACO≌⊿∠CBD ∴BD=OC=1 CD=OA=2 ∵点A(0,2) 点C(1,0)∴OA=2 OC=1∴点B(3,1)2013.10
知
三
点已
知
与x轴的交点 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CBO=60°∠CAB=30°a=? b=?A( ) B( )OA=? OB=?⊿ABCa=? b=?两个点可解 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CAB=60°∠CAB=30°解:在Rt⊿AOC中:∠OAC=30°OC=在Rt⊿BOC中:∠CBO=60°OC=∴∴ 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CBO=60°∠CAB=30°设A( ) B( ) C( )OA=? OB=?⊿ABC可解 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式. 探究1∠CAB=60°∠CAB=45°解:在Rt⊿AOC中:∠OAC=30°OC=在Rt⊿BOC中:∠CBO=60°OC=∴∴ 例1 已知抛物线y=ax2+bx+ 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=30°,求抛物线的解析式. 探究1∠CAB=60°∠CAB=30°解:在Rt⊿AOC中:∠OAC=30°OC=在Rt⊿BOC中:∠CBO=60°OC=一
个
点探究2 例2 二次函数 的图象与x轴交于A、
B,与y轴交于点C,A、C的坐标分别是(1,0和(0,2),
B在A的右侧,且∠OCA=∠OBC.求这个二次函数的解析式.(1,0)(0,2)⊿AOC∽⊿COB设A( ) B( ) C( )1,00,2OB=?比例式法解直角三角形(1,0)(0,2)解:∴∴∵ ∠OCA=∠OBC, ∠AOC=∠BOC=Rt∠∴⊿ AOC ∽ ⊿ COB∵ A(1,0) C(0,2)∴ OA=1 OC=2(1,0)(0,2)解:∵ ∠OCA=∠OBC, ∠AOC=∠BOC=Rt∠∴⊿ AOC ∽ ⊿ COB∵ A(1,0) C(0,2)∴ OA=1 OC=2(4,0)一
个
点 例3 二次函数图象过A、C、B三点,点A的坐标为(-1,0,点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.求抛物线的解析式探究3(-1,0)(4,0)C(0,5)设a=?一个点( ) 例3 二次函数图象过A、C、B三点,点A的坐标为(-1,0,点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.求抛物线的解析式探究3(-1,0)(4,0)C(4,0)解:∵A(-1,0) B(4,0)∵AB=OC 例4 如图所示,现将一块等腰直角三角板ABC放在第一象
限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),
抛物线y=ax2+ax-2经过点B.求抛物线的解析式.探究4OA=2OC=1 a=?一个点( )点B( , )相关线段的长度DOD=? BD=?∟⊿ ∽ ⊿≌⊿AOC ≌⊿CDBOD=3BD=OC=1B(3,1)探究4OA=2OC=1D解:过点B作BD⊥x轴,垂足为D∵∠ACB=Rt∠∴∠ACO=∠CBD∵AC=BC ∠A0C=∠CDB ∠ACO=∠CBD ∴⊿ACO≌⊿∠CBD ∴BD=OC=1 CD=OA=2 ∵点A(0,2) 点C(1,0)∴OA=2 OC=1∴点B(3,1)2013.10
