8.2 角的度量(课件)苏教版四年级上册数学(共16张PPT)
文档属性
| 名称 | 8.2 角的度量(课件)苏教版四年级上册数学(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 756.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-25 06:59:32 | ||
图片预览






文档简介
(共16张PPT)
2 角的度量
第八单元 垂线与平行线
1.认识量角器的计量单位,了解量角器的构造特点,掌握正确地读写角的度数的方法。
2.在观察中发现量角器的构造和量角的原理,经历量角方法的探究过程,感受量角的意义。
从一点起画两条( 射线 ),可以组成一个角,角通常用符号“( ∠ )”来表示,右图中的角可以记作( ∠A )。
射线
∠
∠A
在教学中,教师要引导学生在充分观察的基础上,明确测量角的大小时的“两个重合”和从0°开始数角的大小方法,避免内圈测量记外圈度数的错误。
任务驱动
阅读教材例3的内容,尝试解决下列问题。
1.我们身边有哪些地方有角?
桌子有角,黑板有角,三角尺有角……
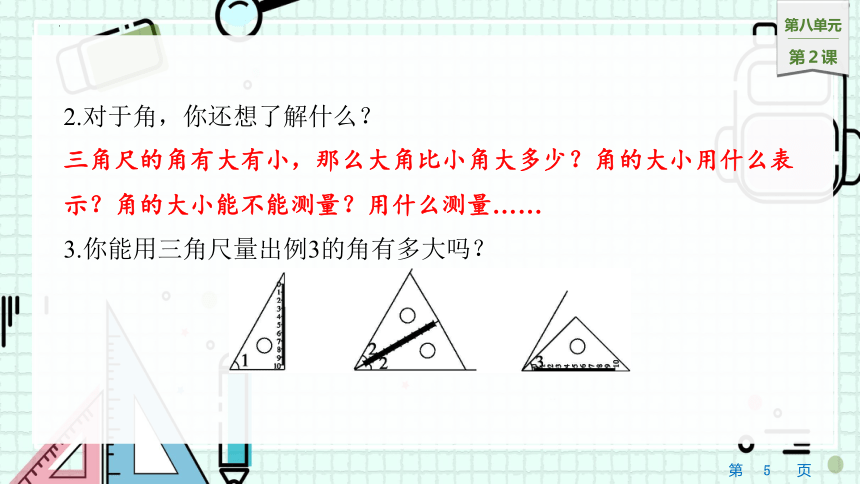
2.对于角,你还想了解什么?
三角尺的角有大有小,那么大角比小角大多少?角的大小用什么表示?角的大小能不能测量?用什么测量……
3.你能用三角尺量出例3的角有多大吗?
用∠1量,正好与∠1一样大;用∠2量,有2个∠2那么大;用∠3量,比∠3大一些。这些方法都不能准确地表示角的大小,而且还很混乱,为了准确地测量角的大小,要有统一的度量工具和计量单位,这个工具就是量角器。量角器是人们用来测量角的大小的工具。
4.仔细观察,说一说量角器上有什么。
量角器的中心是一个点,叫中心点。量角器上有许多刻度,从中心到各刻度之间的连线叫作刻度线。为了方便使用,量角器上有两条0°刻度线和两圈刻度,一个是内圈刻度,一个是外圈刻度。
5.小组讨论:怎样用量角器量出下面两个角的度数?
(1)用量角器量角的时候,把量角器放在角的上面,使量角器的中心点和角的顶点重合。
(2)0°刻度线和角的一条边重合。
(3)角的另一条边所对的量角器上的刻度,就是这个角的度数。
∠1=60° ∠2=120°
6.量一量,并比较下面两个角的大小,你有什么发现?
角的大小与角的两边长短没有关系
(1)量一量:∠1=( 60° ),∠2=( 60° )
60°
60°
(2)∠1的两条边比较( 短 ),∠2的两条边比较( 长 ),但是∠1和∠2都等于( 60° )
发现:角的大小与角的两边开口的大小有关,与角的两边长短没有关系。
短
长
60°
角的大小与角的两边开口的大小有关,与角的两边长短没有
关系。
量角时,量角器的( 中心点 )和角的( 顶点 )重合,( 刻度 )线和角的( 一条边 )重合。
归纳总结
1.度量角的工具是量角器,“度”是计量角的单位。
2.量角的度数时要做到量角器的中心点与角的顶点重合。
中心点
顶点
刻度
一条边
●即时巩固
填空题。
1.填空题。
(1)从一点引出两条( 射线 )可以组成一个( 角 ),这个点叫作角的( 顶点 ),这两条( 射线 )叫作角的( 边 ),角通常用符号( ∠ )表示。
(2)角的大小和角的两边( 开口 )的大小有关。
射线
角
顶点
射线
边
∠
开口
2.精心挑选。
(1)度量一个角,角的一条边对着量角器上内圈“0”刻度,另一条边对着内圈刻度“60”,这个角的度数是( A )。
A.60度 B.180度 C.20度
(2)用一个5倍的放大镜看一个15度的角,这个角的度数是( A )。
A.15度 B.20度 C.75度
A
A
3.量一量,填一填。
∠1=( 70 )°
∠2=( 50 )°
∠3=( 60 )°
三个内角度数的和是( 180 )°
70
50
60
180
∠1=( 30 )°
∠2=( 90 )°
∠3=( 60 )°
三个内角度数的和是( 180 )°
30
90
60
180
END
感谢观看 下节课再会
2 角的度量
第八单元 垂线与平行线
1.认识量角器的计量单位,了解量角器的构造特点,掌握正确地读写角的度数的方法。
2.在观察中发现量角器的构造和量角的原理,经历量角方法的探究过程,感受量角的意义。
从一点起画两条( 射线 ),可以组成一个角,角通常用符号“( ∠ )”来表示,右图中的角可以记作( ∠A )。
射线
∠
∠A
在教学中,教师要引导学生在充分观察的基础上,明确测量角的大小时的“两个重合”和从0°开始数角的大小方法,避免内圈测量记外圈度数的错误。
任务驱动
阅读教材例3的内容,尝试解决下列问题。
1.我们身边有哪些地方有角?
桌子有角,黑板有角,三角尺有角……
2.对于角,你还想了解什么?
三角尺的角有大有小,那么大角比小角大多少?角的大小用什么表示?角的大小能不能测量?用什么测量……
3.你能用三角尺量出例3的角有多大吗?
用∠1量,正好与∠1一样大;用∠2量,有2个∠2那么大;用∠3量,比∠3大一些。这些方法都不能准确地表示角的大小,而且还很混乱,为了准确地测量角的大小,要有统一的度量工具和计量单位,这个工具就是量角器。量角器是人们用来测量角的大小的工具。
4.仔细观察,说一说量角器上有什么。
量角器的中心是一个点,叫中心点。量角器上有许多刻度,从中心到各刻度之间的连线叫作刻度线。为了方便使用,量角器上有两条0°刻度线和两圈刻度,一个是内圈刻度,一个是外圈刻度。
5.小组讨论:怎样用量角器量出下面两个角的度数?
(1)用量角器量角的时候,把量角器放在角的上面,使量角器的中心点和角的顶点重合。
(2)0°刻度线和角的一条边重合。
(3)角的另一条边所对的量角器上的刻度,就是这个角的度数。
∠1=60° ∠2=120°
6.量一量,并比较下面两个角的大小,你有什么发现?
角的大小与角的两边长短没有关系
(1)量一量:∠1=( 60° ),∠2=( 60° )
60°
60°
(2)∠1的两条边比较( 短 ),∠2的两条边比较( 长 ),但是∠1和∠2都等于( 60° )
发现:角的大小与角的两边开口的大小有关,与角的两边长短没有关系。
短
长
60°
角的大小与角的两边开口的大小有关,与角的两边长短没有
关系。
量角时,量角器的( 中心点 )和角的( 顶点 )重合,( 刻度 )线和角的( 一条边 )重合。
归纳总结
1.度量角的工具是量角器,“度”是计量角的单位。
2.量角的度数时要做到量角器的中心点与角的顶点重合。
中心点
顶点
刻度
一条边
●即时巩固
填空题。
1.填空题。
(1)从一点引出两条( 射线 )可以组成一个( 角 ),这个点叫作角的( 顶点 ),这两条( 射线 )叫作角的( 边 ),角通常用符号( ∠ )表示。
(2)角的大小和角的两边( 开口 )的大小有关。
射线
角
顶点
射线
边
∠
开口
2.精心挑选。
(1)度量一个角,角的一条边对着量角器上内圈“0”刻度,另一条边对着内圈刻度“60”,这个角的度数是( A )。
A.60度 B.180度 C.20度
(2)用一个5倍的放大镜看一个15度的角,这个角的度数是( A )。
A.15度 B.20度 C.75度
A
A
3.量一量,填一填。
∠1=( 70 )°
∠2=( 50 )°
∠3=( 60 )°
三个内角度数的和是( 180 )°
70
50
60
180
∠1=( 30 )°
∠2=( 90 )°
∠3=( 60 )°
三个内角度数的和是( 180 )°
30
90
60
180
END
感谢观看 下节课再会
