2022-2023学年华东师大版八年级数学下册17.4 反比例函数练习(含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学下册17.4 反比例函数练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 444.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-26 00:00:00 | ||
图片预览

文档简介
华师大版八下 17.4 反比例函数
一、选择题(共20小题)
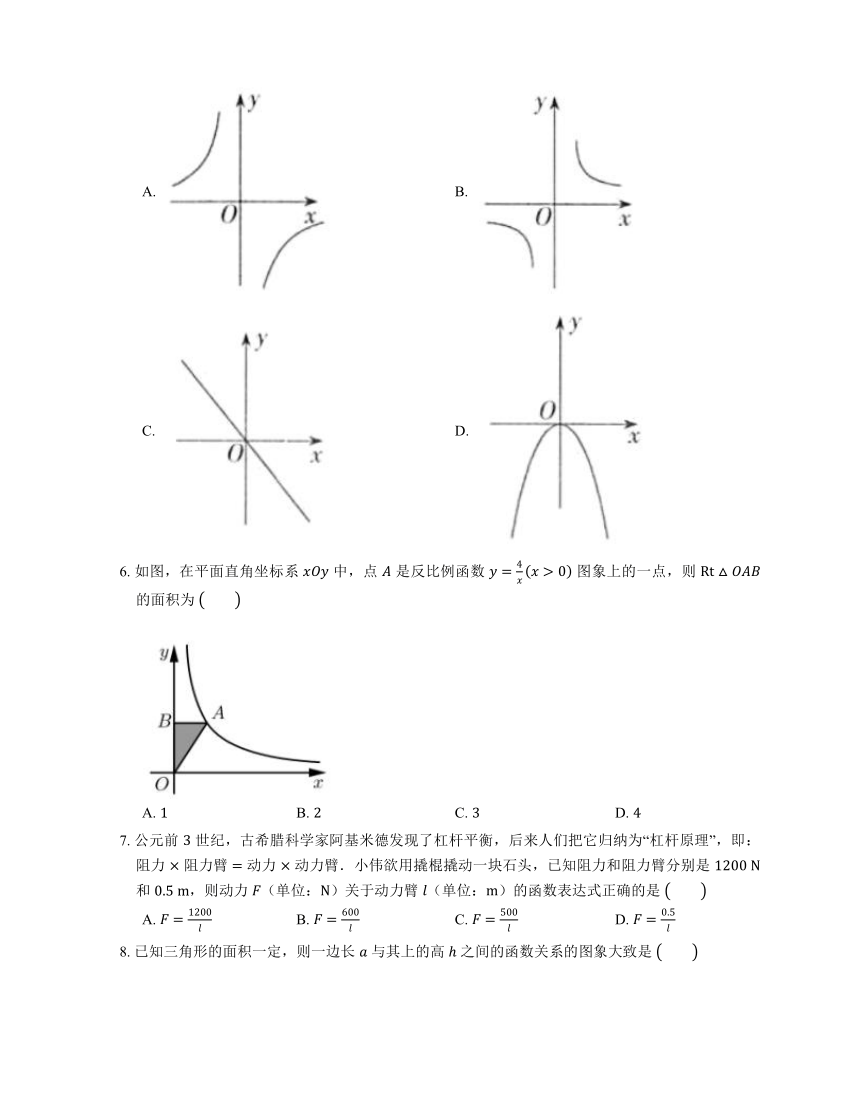
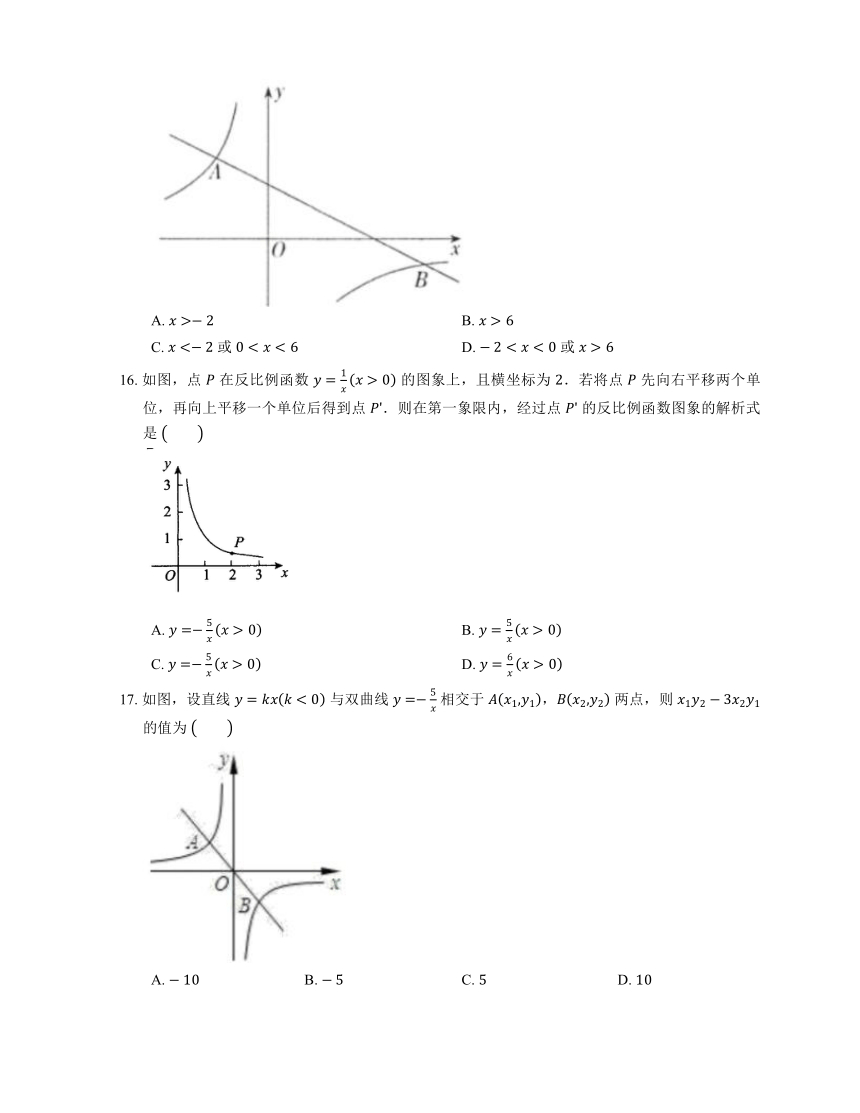
1. 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 是气球体积 的反比例函数,其图象如图所示,当气球内的气压大于 时,气球将爆炸,为了安全,气球的体积应该
A. 不小于 B. 小于 C. 不大于 D. 小于
2. 已知 与 成反比例函数,当 时,,则这个函数的解析式是
A. B. C. D.
3. 如图,正比例函数 的图象与反比例函数 的图象相交于 , 两点,其中点 的横坐标为 ,当 时, 的取值范围是
A. B.
C. D.
4. 下列关系式中, 是 的反比例函数的是
A. B. C. D.
5. 函数 的图象大致是
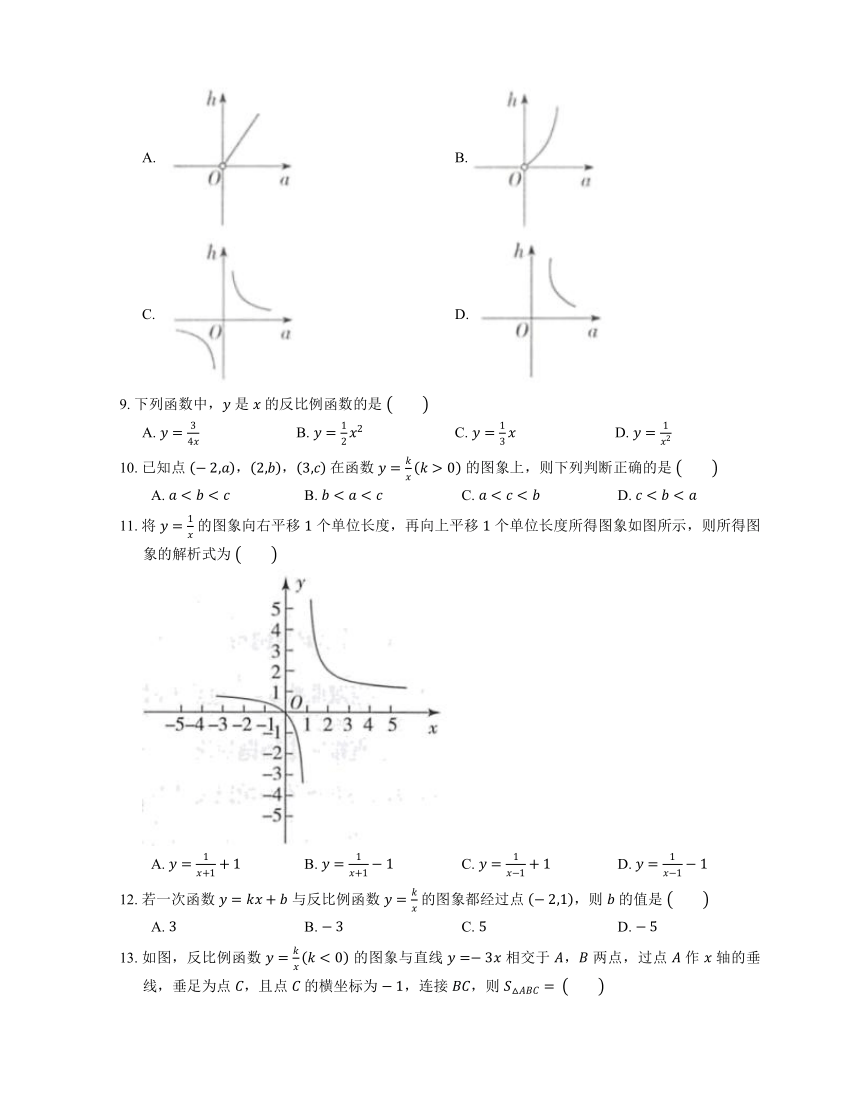
A. B.
C. D.
6. 如图,在平面直角坐标系 中,点 是反比例函数 图象上的一点,则 的面积为
A. B. C. D.
7. 公元前 世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力 阻力臂 动力 动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力 (单位:)关于动力臂 (单位:)的函数表达式正确的是
A. B. C. D.
8. 已知三角形的面积一定,则一边长 与其上的高 之间的函数关系的图象大致是
A. B.
C. D.
9. 下列函数中, 是 的反比例函数的是
A. B. C. D.
10. 已知点 ,, 在函数 的图象上,则下列判断正确的是
A. B. C. D.
11. 将 的图象向右平移 个单位长度,再向上平移 个单位长度所得图象如图所示,则所得图象的解析式为
A. B. C. D.
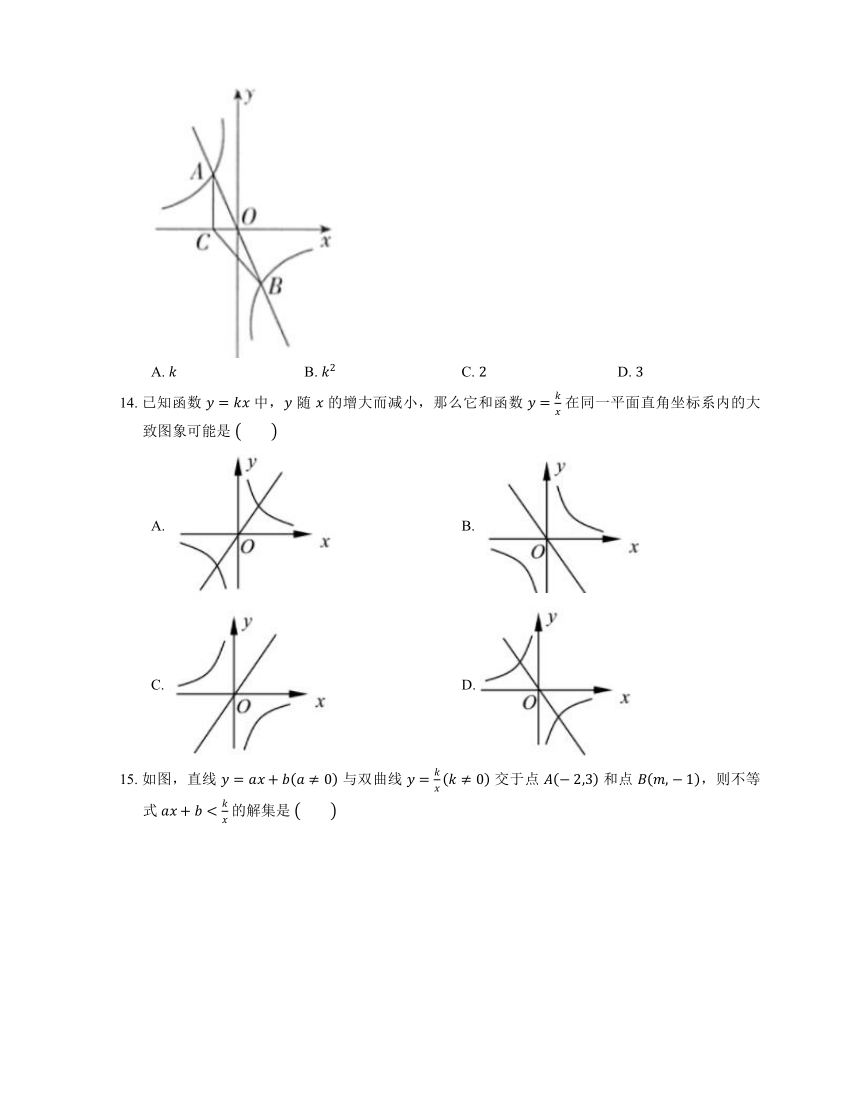
12. 若一次函数 与反比例函数 的图象都经过点 ,则 的值是
A. B. C. D.
13. 如图,反比例函数 的图象与直线 相交于 , 两点,过点 作 轴的垂线,垂足为点 ,且点 的横坐标为 ,连接 ,则
A. B. C. D.
14. 已知函数 中, 随 的增大而减小,那么它和函数 在同一平面直角坐标系内的大致图象可能是
A. B.
C. D.
15. 如图,直线 与双曲线 交于点 和点 ,则不等式 的解集是
A. B.
C. 或 D. 或
16. 如图,点 在反比例函数 的图象上,且横坐标为 .若将点 先向右平移两个单位,再向上平移一个单位后得到点 .则在第一象限内,经过点 的反比例函数图象的解析式是
A. B.
C. D.
17. 如图,设直线 与双曲线 相交于 , 两点,则 的值为
A. B. C. D.
18. 在平面直角坐标系中,反比例函数 与一次函数 的图象如图所示,则图中的阴影部分的面积最大的是
A. B.
C. D.
19. 如图,点 , 是反比例函数 图象上的两点,过点 , 分別作 于点 , 于点 ,连接 ,,已知点 ,,,则 等于
A. B. C. D.
20. 一次函数 与反比例函数 的图象在第一象限内有两个不同的交点,那么下列判断正确的是
A. , B. , C. , D. ,
二、填空题(共6小题)
21. 如果反比例函数 ( 是常数,)的图象经过点 ,那么当 时, 的值随 的值增大而 .(填“增大”或“减小”)
22. 已知点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,若反比例函数图象经过点 ,则该反比例函数的解析式为 .
23. 若函数 是 关于 的反比例函数,则 的值为 .
24. 已知反比例函数 的图象如图所示,请结合图象回答:当 时,自变量 的取值范围是 .
25. 如图,点 是反比例函数 图象上的一点,则矩形 的面积是 .
26. 如图,点 , 在反比例函数 的图象上,, 的纵坐标分别是 ,,连接 ,,则 的面积是 .
三、解答题(共7小题)
27. 如图所示是一位学生所画的一个反比例函数的图象,你认为这个图象正确吗
28. 如图,平行于 轴的直尺(一部分)与双曲线 交于点 和 ,与 轴交于点 和 .点 和 的刻度分别为 和 ,直尺的宽度为 ,.(注:平面直角坐标系内一个单位长度为 )
(1)点 的坐标为 ;
(2)求双曲线 的解析式;
(3)若经过 , 两点的直线解析式为 ,请直接写出关于 的不等式 的解集.
29. 已知反比例函数 .
(1)若该反比例函数的图象与直线 只有一个公共点,求 的值;
(2)如图,反比例函数 的图象记为曲线 ,将 向左平移 个单位长度,得曲线 ,请在图中画出 ,并直接写出 平移至 处所扫过的面积.
30. 如图,在直角坐标平面内,直线 与 轴, 轴交于点 ,,且与函数 (, 是常数)的图象交于 ,,其中 .过点 作 轴的垂线,垂足为 ,过点 作 轴的垂线,垂足为 ,连接 ,,.
(1)若 的面积为 ,求点 的坐标;
(2)若四边形 是等腰梯形,求直线 的表达式.
31. 已知正比例函数 ( 为常数,)的图象与反比例函数 ( 为常数,)的图象有一个交点的横坐标是 .
(1)求这两个函数图象的交点坐标;
(2)若点 , 是反比例函数 图象上的两点,且 ,试比较 , 的大小.
32. 已知 ,并且 与 成正比例, 与 成反比例.当 时,;当 时,.求 关于 的函数解析式.
33. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
(1)求该反比例函数的表达式;
(2)若点 在 轴上,且 的面积为 ,求点 的坐标.
答案
1. A
【解析】设气球内气体的气压 和气体体积 的关系式为 ,
因为图象过点 ,
所以 ,即 ,
当 时,,
因为在第一象限内, 随 的增大而减小,
所以当 时,.
2. A
3. D
4. C
【解析】 是一次函数;
可化为 ,是一次函数;
是反比例函数;
是二次函数.
5. B
【解析】 是反比例函数,其中 ,
函数图象是双曲线,位于第一、第三象限,只有B选项符合题意.
6. B
【解析】 点 是反比例函数 图象上的一点,
由反比例函数的几何意义可知:
.
7. B
【解析】因为阻力 阻力臂 动力 动力臂,
所以 ,
所以 .
8. D
【解析】由三角形面积公式得 ,即 ,已知三角形的面积 一定,则 是 的反比例函数,又 ,,故其图象为双曲线在第一象限的分支.故选D.
9. A
【解析】 可化为 ,是反比例函数,符合题意;,, 都不是反比例函数.故选A.
10. C
【解析】,
函数 的图象分布在第一、三象限,在每一象限, 随 的增大而减小,
,
,,
.
11. C
【解析】由“左加右减”的原则可知, 的图象向右平移 个单位长度所得函数图象的解析式是 .
由“上加下减”的原则可知,函数 的图象向上平移 个单位长度所得函数图象的解析式是 .
12. B
【解析】将点 代入解析式,得 ;
再把点 和 代入一次函数,得 ,
解得 .
13. D
【解析】 轴,点 的横坐标为 ,
点 的横坐标为 ,
当 时,,则 ,
,
反比例函数 的图象与直线 都关于原点对称,
点 和点 关于原点对称,
,
,
.
故选D.
14. D
15. D
【解析】把 代入 ,得 ,即 ,
把 代入 ,得 ,即 ,
结合图象可知不等式 的解集昰 或 .
16. D
【解析】 点 在反比例函数 的图象上,且横坐标为 ,
点 的纵坐标为 ,即点 的坐标为 ,
将点 先向右平移两个单位,再向上平移一个单位后得到点 .
点 的坐标为 ,
经过点 的反比例函数图象的解析式为 .
17. A
【解析】由图象可知点 , 关于原点对称,
即 ,,
把 代入双曲线 得 ,则
18. A
【解析】由反比例函数中系数 的几何意义可知,选项A中阴影部分的面积 ,选项B,C,D中的阴影部分的面积都等于 .故选A.
19. D
【解析】,,
,
,
,
,
,
,
,
点 是反比例函数 图象上的点,
,
点 在该反比例函数的图象上.且 ,
.
20. B
21. 增大
22.
【解析】因为点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,
所以 点坐标为: 或 ,
设反比例函数的解析式为 ,
所以 ,
则该反比例函数的解析式为:.
23.
【解析】 函数 是 关于 的反比例函数,
,
解得:.
24.
25.
26.
【解析】 点 , 在反比例函数 的图象上,, 的纵坐标分别是 ,,
,,如图,
易知 ,
,
.
27. 错.反比例函数的图象的两支不能与 轴和 轴相交.
28. (1)
(2) 将 点坐标代入 中,
得 ,
,
双曲线的解析式为 .
(3) 直尺的宽度为 ,
,
,
点 的横坐标为 .
由图象可知,
关于 的不等式 的解集是 或 .
29. (1) 解 得 ,
反比例函数的图象与直线 只有一个公共点,
,
.
(2) 如图所示,
平移至 处所扫过的面积 .
30. (1) 因为点 在函数 上,
所以 ,
所以 ,
所以 ,
因为 的面积为 ,
所以 ,
所以 ,
所以 .
(2) 因为 与 相交于点 ,
所以 与 不平行.
又因为四边形 是等腰梯形,
所以 ,,
又 ,
所以 ,
又 轴,
所以 ,
所以 .
又 ,
所以 ,
所以 ,
所以直线 的表达式为 .
31. (1) 由题意得 ,解得 ,
正比例函数的表达式为 ,反比例函数的表达式为 ,解 得 ,由 得 ,
这两个函数图象的交点坐标为 、 .
(2) 反比例函数 的图象在第一、三象限,且在每个象限内, 随 的增大而减小,
当 时,;
当 时,;
当 时,
,,
.
32. 设 ,,则 ,
代入 ,;, 得
解得
函数解析式为:.
33. (1) 把 代入 中,
得 ,
点 的坐标为 ,
把点 代入 中,
得 ,
反比例函数的解析式为 ;
(2) 过点 作 垂直与 轴,垂足为 ,
设点 的坐标为 ,
点 与点 关于原点对称,
点 的坐标为 ,
,,
,
解得: 或 ,
点 的坐标为 或 .
一、选择题(共20小题)
1. 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 是气球体积 的反比例函数,其图象如图所示,当气球内的气压大于 时,气球将爆炸,为了安全,气球的体积应该
A. 不小于 B. 小于 C. 不大于 D. 小于
2. 已知 与 成反比例函数,当 时,,则这个函数的解析式是
A. B. C. D.
3. 如图,正比例函数 的图象与反比例函数 的图象相交于 , 两点,其中点 的横坐标为 ,当 时, 的取值范围是
A. B.
C. D.
4. 下列关系式中, 是 的反比例函数的是
A. B. C. D.
5. 函数 的图象大致是
A. B.
C. D.
6. 如图,在平面直角坐标系 中,点 是反比例函数 图象上的一点,则 的面积为
A. B. C. D.
7. 公元前 世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力 阻力臂 动力 动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力 (单位:)关于动力臂 (单位:)的函数表达式正确的是
A. B. C. D.
8. 已知三角形的面积一定,则一边长 与其上的高 之间的函数关系的图象大致是
A. B.
C. D.
9. 下列函数中, 是 的反比例函数的是
A. B. C. D.
10. 已知点 ,, 在函数 的图象上,则下列判断正确的是
A. B. C. D.
11. 将 的图象向右平移 个单位长度,再向上平移 个单位长度所得图象如图所示,则所得图象的解析式为
A. B. C. D.
12. 若一次函数 与反比例函数 的图象都经过点 ,则 的值是
A. B. C. D.
13. 如图,反比例函数 的图象与直线 相交于 , 两点,过点 作 轴的垂线,垂足为点 ,且点 的横坐标为 ,连接 ,则
A. B. C. D.
14. 已知函数 中, 随 的增大而减小,那么它和函数 在同一平面直角坐标系内的大致图象可能是
A. B.
C. D.
15. 如图,直线 与双曲线 交于点 和点 ,则不等式 的解集是
A. B.
C. 或 D. 或
16. 如图,点 在反比例函数 的图象上,且横坐标为 .若将点 先向右平移两个单位,再向上平移一个单位后得到点 .则在第一象限内,经过点 的反比例函数图象的解析式是
A. B.
C. D.
17. 如图,设直线 与双曲线 相交于 , 两点,则 的值为
A. B. C. D.
18. 在平面直角坐标系中,反比例函数 与一次函数 的图象如图所示,则图中的阴影部分的面积最大的是
A. B.
C. D.
19. 如图,点 , 是反比例函数 图象上的两点,过点 , 分別作 于点 , 于点 ,连接 ,,已知点 ,,,则 等于
A. B. C. D.
20. 一次函数 与反比例函数 的图象在第一象限内有两个不同的交点,那么下列判断正确的是
A. , B. , C. , D. ,
二、填空题(共6小题)
21. 如果反比例函数 ( 是常数,)的图象经过点 ,那么当 时, 的值随 的值增大而 .(填“增大”或“减小”)
22. 已知点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,若反比例函数图象经过点 ,则该反比例函数的解析式为 .
23. 若函数 是 关于 的反比例函数,则 的值为 .
24. 已知反比例函数 的图象如图所示,请结合图象回答:当 时,自变量 的取值范围是 .
25. 如图,点 是反比例函数 图象上的一点,则矩形 的面积是 .
26. 如图,点 , 在反比例函数 的图象上,, 的纵坐标分别是 ,,连接 ,,则 的面积是 .
三、解答题(共7小题)
27. 如图所示是一位学生所画的一个反比例函数的图象,你认为这个图象正确吗
28. 如图,平行于 轴的直尺(一部分)与双曲线 交于点 和 ,与 轴交于点 和 .点 和 的刻度分别为 和 ,直尺的宽度为 ,.(注:平面直角坐标系内一个单位长度为 )
(1)点 的坐标为 ;
(2)求双曲线 的解析式;
(3)若经过 , 两点的直线解析式为 ,请直接写出关于 的不等式 的解集.
29. 已知反比例函数 .
(1)若该反比例函数的图象与直线 只有一个公共点,求 的值;
(2)如图,反比例函数 的图象记为曲线 ,将 向左平移 个单位长度,得曲线 ,请在图中画出 ,并直接写出 平移至 处所扫过的面积.
30. 如图,在直角坐标平面内,直线 与 轴, 轴交于点 ,,且与函数 (, 是常数)的图象交于 ,,其中 .过点 作 轴的垂线,垂足为 ,过点 作 轴的垂线,垂足为 ,连接 ,,.
(1)若 的面积为 ,求点 的坐标;
(2)若四边形 是等腰梯形,求直线 的表达式.
31. 已知正比例函数 ( 为常数,)的图象与反比例函数 ( 为常数,)的图象有一个交点的横坐标是 .
(1)求这两个函数图象的交点坐标;
(2)若点 , 是反比例函数 图象上的两点,且 ,试比较 , 的大小.
32. 已知 ,并且 与 成正比例, 与 成反比例.当 时,;当 时,.求 关于 的函数解析式.
33. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
(1)求该反比例函数的表达式;
(2)若点 在 轴上,且 的面积为 ,求点 的坐标.
答案
1. A
【解析】设气球内气体的气压 和气体体积 的关系式为 ,
因为图象过点 ,
所以 ,即 ,
当 时,,
因为在第一象限内, 随 的增大而减小,
所以当 时,.
2. A
3. D
4. C
【解析】 是一次函数;
可化为 ,是一次函数;
是反比例函数;
是二次函数.
5. B
【解析】 是反比例函数,其中 ,
函数图象是双曲线,位于第一、第三象限,只有B选项符合题意.
6. B
【解析】 点 是反比例函数 图象上的一点,
由反比例函数的几何意义可知:
.
7. B
【解析】因为阻力 阻力臂 动力 动力臂,
所以 ,
所以 .
8. D
【解析】由三角形面积公式得 ,即 ,已知三角形的面积 一定,则 是 的反比例函数,又 ,,故其图象为双曲线在第一象限的分支.故选D.
9. A
【解析】 可化为 ,是反比例函数,符合题意;,, 都不是反比例函数.故选A.
10. C
【解析】,
函数 的图象分布在第一、三象限,在每一象限, 随 的增大而减小,
,
,,
.
11. C
【解析】由“左加右减”的原则可知, 的图象向右平移 个单位长度所得函数图象的解析式是 .
由“上加下减”的原则可知,函数 的图象向上平移 个单位长度所得函数图象的解析式是 .
12. B
【解析】将点 代入解析式,得 ;
再把点 和 代入一次函数,得 ,
解得 .
13. D
【解析】 轴,点 的横坐标为 ,
点 的横坐标为 ,
当 时,,则 ,
,
反比例函数 的图象与直线 都关于原点对称,
点 和点 关于原点对称,
,
,
.
故选D.
14. D
15. D
【解析】把 代入 ,得 ,即 ,
把 代入 ,得 ,即 ,
结合图象可知不等式 的解集昰 或 .
16. D
【解析】 点 在反比例函数 的图象上,且横坐标为 ,
点 的纵坐标为 ,即点 的坐标为 ,
将点 先向右平移两个单位,再向上平移一个单位后得到点 .
点 的坐标为 ,
经过点 的反比例函数图象的解析式为 .
17. A
【解析】由图象可知点 , 关于原点对称,
即 ,,
把 代入双曲线 得 ,则
18. A
【解析】由反比例函数中系数 的几何意义可知,选项A中阴影部分的面积 ,选项B,C,D中的阴影部分的面积都等于 .故选A.
19. D
【解析】,,
,
,
,
,
,
,
,
点 是反比例函数 图象上的点,
,
点 在该反比例函数的图象上.且 ,
.
20. B
21. 增大
22.
【解析】因为点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,
所以 点坐标为: 或 ,
设反比例函数的解析式为 ,
所以 ,
则该反比例函数的解析式为:.
23.
【解析】 函数 是 关于 的反比例函数,
,
解得:.
24.
25.
26.
【解析】 点 , 在反比例函数 的图象上,, 的纵坐标分别是 ,,
,,如图,
易知 ,
,
.
27. 错.反比例函数的图象的两支不能与 轴和 轴相交.
28. (1)
(2) 将 点坐标代入 中,
得 ,
,
双曲线的解析式为 .
(3) 直尺的宽度为 ,
,
,
点 的横坐标为 .
由图象可知,
关于 的不等式 的解集是 或 .
29. (1) 解 得 ,
反比例函数的图象与直线 只有一个公共点,
,
.
(2) 如图所示,
平移至 处所扫过的面积 .
30. (1) 因为点 在函数 上,
所以 ,
所以 ,
所以 ,
因为 的面积为 ,
所以 ,
所以 ,
所以 .
(2) 因为 与 相交于点 ,
所以 与 不平行.
又因为四边形 是等腰梯形,
所以 ,,
又 ,
所以 ,
又 轴,
所以 ,
所以 .
又 ,
所以 ,
所以 ,
所以直线 的表达式为 .
31. (1) 由题意得 ,解得 ,
正比例函数的表达式为 ,反比例函数的表达式为 ,解 得 ,由 得 ,
这两个函数图象的交点坐标为 、 .
(2) 反比例函数 的图象在第一、三象限,且在每个象限内, 随 的增大而减小,
当 时,;
当 时,;
当 时,
,,
.
32. 设 ,,则 ,
代入 ,;, 得
解得
函数解析式为:.
33. (1) 把 代入 中,
得 ,
点 的坐标为 ,
把点 代入 中,
得 ,
反比例函数的解析式为 ;
(2) 过点 作 垂直与 轴,垂足为 ,
设点 的坐标为 ,
点 与点 关于原点对称,
点 的坐标为 ,
,,
,
解得: 或 ,
点 的坐标为 或 .
