2022-2023学年华东师大版八年级数学下册19.3 正方形同步练习(含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学下册19.3 正方形同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 340.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-26 15:16:44 | ||
图片预览



文档简介
华师大版八下 19.3 正方形
一、选择题(共8小题)
1. 四个角相等,四条边也相等的四边形一定是
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
2. 两条对角线互相平分、互相垂直且相等的四边形是
A. 矩形 B. 菱形
C. 正方形 D. 矩形;菱形或正方形
3. 在下列命题中,是真命题的是
A. 两条对角线相等的四边形是矩形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相平分的四边形是平行四边形
D. 两条对角线互相垂直且相等的四边形是正方形
4. 正方形的面积和它的边长
A. 成正比例 B. 成反比例 C. 不成比例
5. 如图,在反映特殊四边形之间关系的知识结构图中,①②③④表示需要添加的条件,则下列描述错误的是
A. ①表示有一个角是直角 B. ②表示有一组邻边相等
C. ③表示四个角都相等 D. ④表示对角线相等
6. 下列条件可以利用定义说明平行四边形 是正方形的是
A. , B. ,
C. , D. 以上均错
7. 如图,在菱形 中,,它的一个顶点 在反比例函数 的图象上,若 ,则反比例函数的表达式为
A. B. C. D.
8. 如图 ,将正方形 置于平面直角坐标系中,其中 边在 轴上,其余各边均与坐标轴平行,直线 : 沿 轴的负方向以每秒 个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为 ,平移的时间为 (秒), 与 的函数图象如图 所示,则图 中 的值为
A. B. C. D.
二、填空题(共9小题)
9. 菱形 的对角线相交于点 ,请你添加一个条件使得该菱形为正方形,添加的条件是 .
10. 如图,正方形 边长为 ,点 是 延长线上的一点,那么 面积是 , 的面积是 .
11. 正方形的一条对角线长为 ,那么其面积是 .
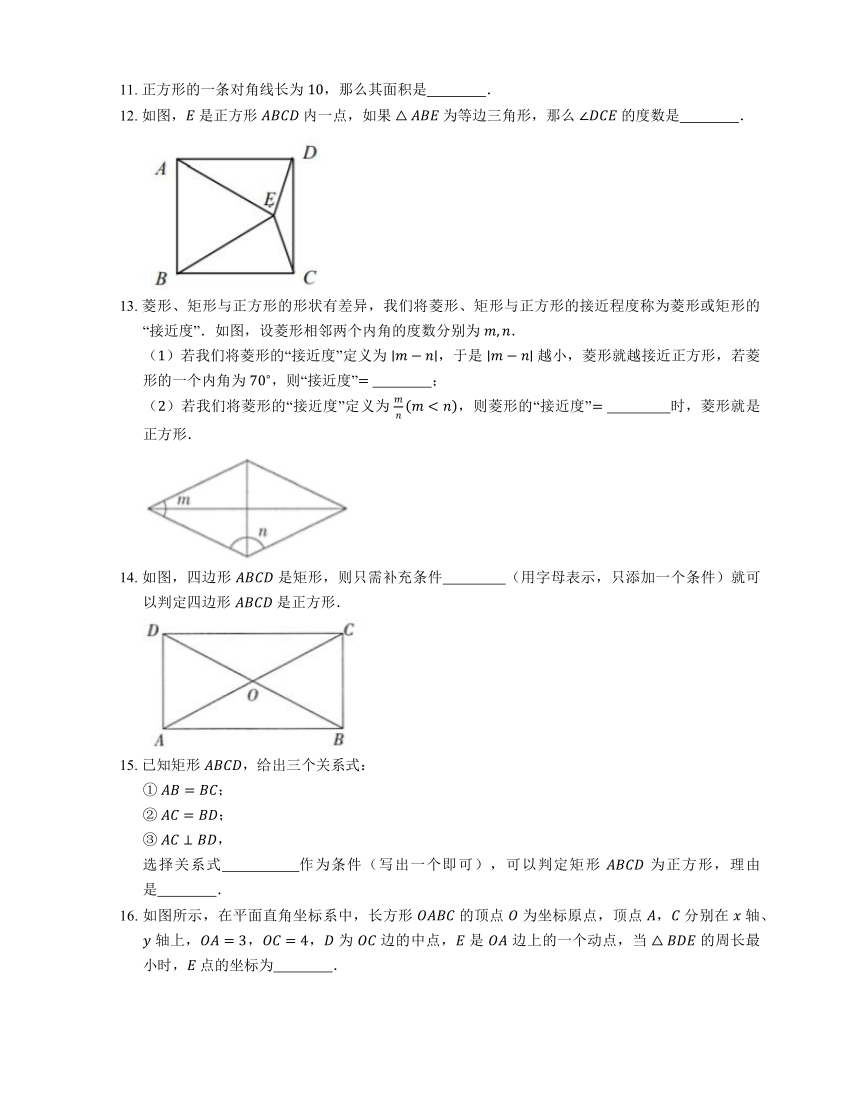
12. 如图, 是正方形 内一点,如果 为等边三角形,那么 的度数是 .
13. 菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.如图,设菱形相邻两个内角的度数分别为 .
()若我们将菱形的“接近度”定义为 ,于是 越小,菱形就越接近正方形,若菱形的一个内角为 ,则“接近度” ;
()若我们将菱形的“接近度”定义为 ,则菱形的“接近度” 时,菱形就是正方形.
14. 如图,四边形 是矩形,则只需补充条件 (用字母表示,只添加一个条件)就可以判定四边形 是正方形.
15. 已知矩形 ,给出三个关系式:
① ;
② ;
③ ,
选择关系式 作为条件(写出一个即可),可以判定矩形 为正方形,理由是 .
16. 如图所示,在平面直角坐标系中,长方形 的顶点 为坐标原点,顶点 , 分别在 轴、 轴上,,, 为 边的中点, 是 边上的一个动点,当 的周长最小时, 点的坐标为 .
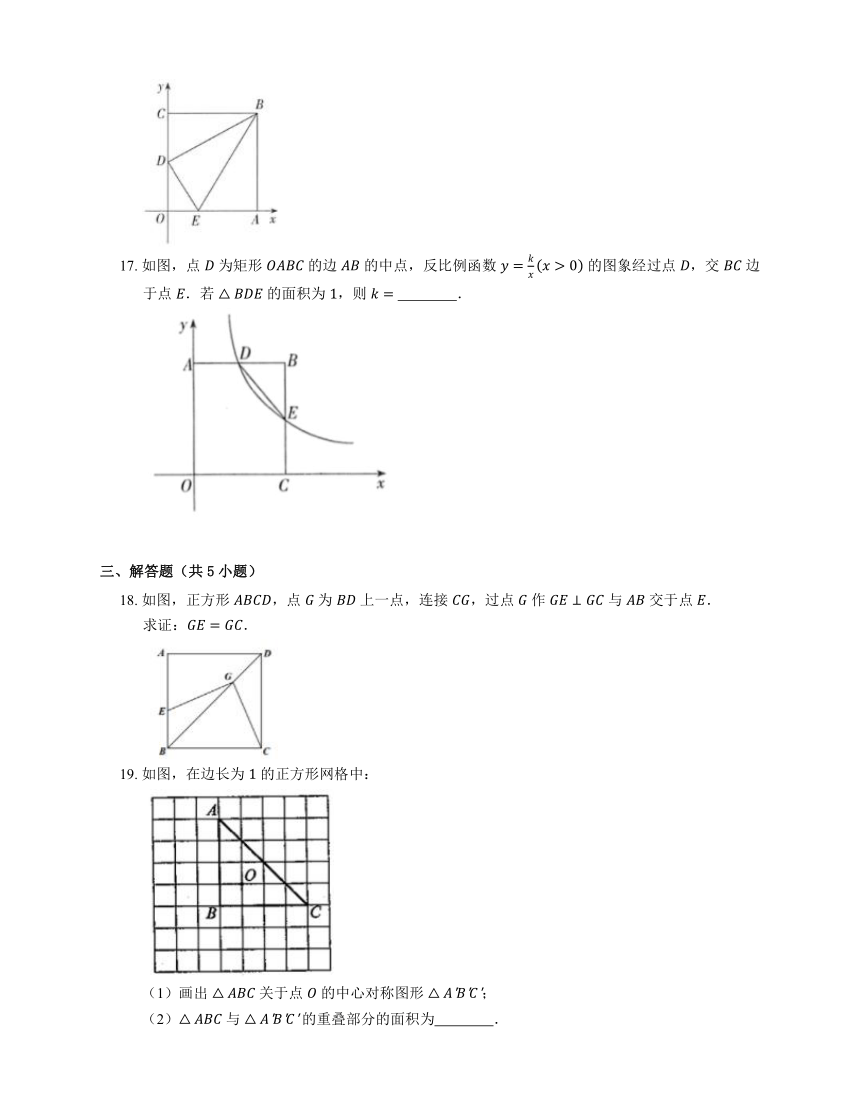
17. 如图,点 为矩形 的边 的中点,反比例函数 的图象经过点 ,交 边于点 .若 的面积为 ,则 .
三、解答题(共5小题)
18. 如图,正方形 ,点 为 上一点,连接 ,过点 作 与 交于点 .
求证:.
19. 如图,在边长为 的正方形网格中:
(1)画出 关于点 的中心对称图形 ;
(2) 与 的重叠部分的面积为 .
20. 如图,平行四边形 的对角线 , 相交于点 ,且 ,,.
(1)求证:四边形 是菱形;
(2)若 ,则当四边形 的形状是 时,四边形 的面积取得最大值,最大值为 .
21. 折纸中的数学问题
【阅读】大约在西汉中期,中国人造出了最早的真正意义上的纸,当时的纸张是以大麻和少量苎麻纤维制造的.在公元 世纪中期,唐朝的折纸艺术伴随着美好祝福传播到了更广泛的世界各国.公元 世纪,处于文化鼎盛时期的阿拉伯人独立发展了折纸艺术,他们为折纸所做的最大贡献在于,将欧洲几何学原理运用到折纸中,并且利用折纸来研究几何学,这是折纸与数学相结合的开始. 世纪之后,折纸艺术与自然科学结合到了一起,它开始成为教育教学和科学研究的工具.请同学们以小组为单位,根据图示进行折纸,完成报告单.
(1)【实践 】请同学们准备一张正方形纸片,按以下步骤进行操作.
第一步:先将正方形 对折,使 与 重合,折痕为 ;把这个正方形展平,然后继续对折,使 与 重合,折痕为 ,再把这个正方形展平,设 和 相交于点 ;
第二步:沿直线 折叠,使点 落在 上,对应点为 ;再沿直线 折叠,使点 落在 上,对应点为 ;
第三步:设 , 分别与 相交于点 ,,分别连接 ,,,.
请你探究:四边形 是正方形吗 请尝试说明理由.
(2)【实践 】请同学们准备一张正方形纸片,按以下步骤进行操作.
第一步:将正方形纸张 的边 与 对折,得到折痕 .
第二步:再将边 向内翻折,使得点 恰好落在 上.
第三步:将边 向内翻折使得点 恰好落在 上.
任务 :
()所形成的三角形 一定是等边三角形.请证明.
()还有其他方法利用正方形纸片折出等边三角形吗
任务 :请小组同学之间比较一下用相同大小的正方形纸片折出等边三角形的面积,有区别吗 如果有,谁折出的等边三角形面积最大 怎么折的呢
22. 以 的三边 ,, 为边在 的同侧作等边三角形,分别是:,,,连接 ,,当四边形 存在时,请填写如表:
答案
1. A
2. C
3. C
4. C
5. C
6. B
【解析】正方形定义中需要的条件是一个角是直角,一组邻边相等的平行四边形,符合这一条件的只有选项B.
7. D
【解析】过点 作 于点 ,
在菱形 中,,,
,,
,
,,则 ,
顶点 在反比例函数 的图象上,
,
反比例函数的表达式为 .
故选D.
8. A
【解析】如图 ,
直线 中,令 ,得 ;令 ,得 ,
即直线 与坐标轴围成的 为等腰直角三角形,
所以直线 与直线 平行,即直线 沿 轴的负方向平移时,同时经过 , 两点,
由图 可得,
时,直线 经过点 ,
所以 ,
所以 ,
由图 可得, 时,直线 经过点 ,
所以当 时,直线 经过 , 两点,
所以 ,
所以等腰 中,,
即当 时,.
9. (答案不唯一)
10. ,
11.
12.
13. ,
【解析】()若菱形的一个内角为 ,则与该内角相邻的角的度数为 ,
“接近度”.
()当菱形的“接近度”等于 时,菱形相邻的两个内角相等,都是 ,则菱形是正方形.
14. (答案不唯一)
【解析】有一组邻边相等的矩形是正方形,故答案为 (答案不唯一).
15. ③,对角线互相垂直的矩形是正方形
16.
【解析】如图,作点 关于 轴的对称点 ,连接 交 轴于 ,
则 .
则 的周长为 ,
的中点,
,
和 关于 轴对称,
.易得 .
设直线 的解析式为 (),
把 , 分别代入得
解得
直线 的解析式为 ,
当 时,,故 点的坐标为 .
17.
【解析】设点 ,
因为点 为矩形 的边 的中点,
所以 ,
所以 ,
因为 的面积为 ,
所以 ,
解得 .
18. 连接 ,利用 ,得 ,又易得 ,得证.
19. (1) 如图
(2)
20. (1) ,,
四边形 是平行四边形.
四边形 是平行四边形,
.
,
,
平行四边形 是矩形,
,
.
平行四边形 是菱形.
(2) 正方形;
【解析】过点 作 的垂线段 交 于点 ,
,
矩形 的面积为 ,
当 与 垂直时, 的长达到最大值,即 长的一半,此时矩形的面积为 .
当 与 垂直时,平行四边形 是正方形.
21. (1) 四边形 是正方形.连接 ,.
易证 ,.根据同角的余角相等可得:,
因此 .
接下来易证 ,故 ,同理 .
由对称性 ,故 .
由两次对折可得:.
因此 ,可得四边形 是矩形.
由对折知 ,
四边形 是正方形.
(2) 任务 .
() 是等边三角形.
证明:易证 ,故 是等腰三角形.
再证 ,且 .因此 ,
是等边三角形.
()如实践 中步骤操作,其中 ,,, 均为等边三角形.
.将正方形对折、再对折.
.正方形纸展开,可以看到折痕 和 .将正方形其中一个角 向上折,折到折痕 位置,标记字母 .
.连接 ,.得到等边三角形 .
任务 .
本作业建议采用等第制评价方式以下评价标准可供参考:
优秀:能证明等边三角形,正确计算等边三角形面积,折纸过程清晰,画图准确,测量准确度高;汇报交流时,内容清晰、交流自信、表达流畅;
良好:能证明等边三角形,正确计算等边三角形面积,折纸过程清晰,画图基本准确,测量准确度较高;汇报交流时,内容清晰、交流自信、表达流畅;
合格:能证明等边三角形,折纸过程清晰,画图达标,测量准确度较高;汇报交流时,内容清晰、交流自信、表达流畅.
22. 平行四边形;;;,
一、选择题(共8小题)
1. 四个角相等,四条边也相等的四边形一定是
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
2. 两条对角线互相平分、互相垂直且相等的四边形是
A. 矩形 B. 菱形
C. 正方形 D. 矩形;菱形或正方形
3. 在下列命题中,是真命题的是
A. 两条对角线相等的四边形是矩形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相平分的四边形是平行四边形
D. 两条对角线互相垂直且相等的四边形是正方形
4. 正方形的面积和它的边长
A. 成正比例 B. 成反比例 C. 不成比例
5. 如图,在反映特殊四边形之间关系的知识结构图中,①②③④表示需要添加的条件,则下列描述错误的是
A. ①表示有一个角是直角 B. ②表示有一组邻边相等
C. ③表示四个角都相等 D. ④表示对角线相等
6. 下列条件可以利用定义说明平行四边形 是正方形的是
A. , B. ,
C. , D. 以上均错
7. 如图,在菱形 中,,它的一个顶点 在反比例函数 的图象上,若 ,则反比例函数的表达式为
A. B. C. D.
8. 如图 ,将正方形 置于平面直角坐标系中,其中 边在 轴上,其余各边均与坐标轴平行,直线 : 沿 轴的负方向以每秒 个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为 ,平移的时间为 (秒), 与 的函数图象如图 所示,则图 中 的值为
A. B. C. D.
二、填空题(共9小题)
9. 菱形 的对角线相交于点 ,请你添加一个条件使得该菱形为正方形,添加的条件是 .
10. 如图,正方形 边长为 ,点 是 延长线上的一点,那么 面积是 , 的面积是 .
11. 正方形的一条对角线长为 ,那么其面积是 .
12. 如图, 是正方形 内一点,如果 为等边三角形,那么 的度数是 .
13. 菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.如图,设菱形相邻两个内角的度数分别为 .
()若我们将菱形的“接近度”定义为 ,于是 越小,菱形就越接近正方形,若菱形的一个内角为 ,则“接近度” ;
()若我们将菱形的“接近度”定义为 ,则菱形的“接近度” 时,菱形就是正方形.
14. 如图,四边形 是矩形,则只需补充条件 (用字母表示,只添加一个条件)就可以判定四边形 是正方形.
15. 已知矩形 ,给出三个关系式:
① ;
② ;
③ ,
选择关系式 作为条件(写出一个即可),可以判定矩形 为正方形,理由是 .
16. 如图所示,在平面直角坐标系中,长方形 的顶点 为坐标原点,顶点 , 分别在 轴、 轴上,,, 为 边的中点, 是 边上的一个动点,当 的周长最小时, 点的坐标为 .
17. 如图,点 为矩形 的边 的中点,反比例函数 的图象经过点 ,交 边于点 .若 的面积为 ,则 .
三、解答题(共5小题)
18. 如图,正方形 ,点 为 上一点,连接 ,过点 作 与 交于点 .
求证:.
19. 如图,在边长为 的正方形网格中:
(1)画出 关于点 的中心对称图形 ;
(2) 与 的重叠部分的面积为 .
20. 如图,平行四边形 的对角线 , 相交于点 ,且 ,,.
(1)求证:四边形 是菱形;
(2)若 ,则当四边形 的形状是 时,四边形 的面积取得最大值,最大值为 .
21. 折纸中的数学问题
【阅读】大约在西汉中期,中国人造出了最早的真正意义上的纸,当时的纸张是以大麻和少量苎麻纤维制造的.在公元 世纪中期,唐朝的折纸艺术伴随着美好祝福传播到了更广泛的世界各国.公元 世纪,处于文化鼎盛时期的阿拉伯人独立发展了折纸艺术,他们为折纸所做的最大贡献在于,将欧洲几何学原理运用到折纸中,并且利用折纸来研究几何学,这是折纸与数学相结合的开始. 世纪之后,折纸艺术与自然科学结合到了一起,它开始成为教育教学和科学研究的工具.请同学们以小组为单位,根据图示进行折纸,完成报告单.
(1)【实践 】请同学们准备一张正方形纸片,按以下步骤进行操作.
第一步:先将正方形 对折,使 与 重合,折痕为 ;把这个正方形展平,然后继续对折,使 与 重合,折痕为 ,再把这个正方形展平,设 和 相交于点 ;
第二步:沿直线 折叠,使点 落在 上,对应点为 ;再沿直线 折叠,使点 落在 上,对应点为 ;
第三步:设 , 分别与 相交于点 ,,分别连接 ,,,.
请你探究:四边形 是正方形吗 请尝试说明理由.
(2)【实践 】请同学们准备一张正方形纸片,按以下步骤进行操作.
第一步:将正方形纸张 的边 与 对折,得到折痕 .
第二步:再将边 向内翻折,使得点 恰好落在 上.
第三步:将边 向内翻折使得点 恰好落在 上.
任务 :
()所形成的三角形 一定是等边三角形.请证明.
()还有其他方法利用正方形纸片折出等边三角形吗
任务 :请小组同学之间比较一下用相同大小的正方形纸片折出等边三角形的面积,有区别吗 如果有,谁折出的等边三角形面积最大 怎么折的呢
22. 以 的三边 ,, 为边在 的同侧作等边三角形,分别是:,,,连接 ,,当四边形 存在时,请填写如表:
答案
1. A
2. C
3. C
4. C
5. C
6. B
【解析】正方形定义中需要的条件是一个角是直角,一组邻边相等的平行四边形,符合这一条件的只有选项B.
7. D
【解析】过点 作 于点 ,
在菱形 中,,,
,,
,
,,则 ,
顶点 在反比例函数 的图象上,
,
反比例函数的表达式为 .
故选D.
8. A
【解析】如图 ,
直线 中,令 ,得 ;令 ,得 ,
即直线 与坐标轴围成的 为等腰直角三角形,
所以直线 与直线 平行,即直线 沿 轴的负方向平移时,同时经过 , 两点,
由图 可得,
时,直线 经过点 ,
所以 ,
所以 ,
由图 可得, 时,直线 经过点 ,
所以当 时,直线 经过 , 两点,
所以 ,
所以等腰 中,,
即当 时,.
9. (答案不唯一)
10. ,
11.
12.
13. ,
【解析】()若菱形的一个内角为 ,则与该内角相邻的角的度数为 ,
“接近度”.
()当菱形的“接近度”等于 时,菱形相邻的两个内角相等,都是 ,则菱形是正方形.
14. (答案不唯一)
【解析】有一组邻边相等的矩形是正方形,故答案为 (答案不唯一).
15. ③,对角线互相垂直的矩形是正方形
16.
【解析】如图,作点 关于 轴的对称点 ,连接 交 轴于 ,
则 .
则 的周长为 ,
的中点,
,
和 关于 轴对称,
.易得 .
设直线 的解析式为 (),
把 , 分别代入得
解得
直线 的解析式为 ,
当 时,,故 点的坐标为 .
17.
【解析】设点 ,
因为点 为矩形 的边 的中点,
所以 ,
所以 ,
因为 的面积为 ,
所以 ,
解得 .
18. 连接 ,利用 ,得 ,又易得 ,得证.
19. (1) 如图
(2)
20. (1) ,,
四边形 是平行四边形.
四边形 是平行四边形,
.
,
,
平行四边形 是矩形,
,
.
平行四边形 是菱形.
(2) 正方形;
【解析】过点 作 的垂线段 交 于点 ,
,
矩形 的面积为 ,
当 与 垂直时, 的长达到最大值,即 长的一半,此时矩形的面积为 .
当 与 垂直时,平行四边形 是正方形.
21. (1) 四边形 是正方形.连接 ,.
易证 ,.根据同角的余角相等可得:,
因此 .
接下来易证 ,故 ,同理 .
由对称性 ,故 .
由两次对折可得:.
因此 ,可得四边形 是矩形.
由对折知 ,
四边形 是正方形.
(2) 任务 .
() 是等边三角形.
证明:易证 ,故 是等腰三角形.
再证 ,且 .因此 ,
是等边三角形.
()如实践 中步骤操作,其中 ,,, 均为等边三角形.
.将正方形对折、再对折.
.正方形纸展开,可以看到折痕 和 .将正方形其中一个角 向上折,折到折痕 位置,标记字母 .
.连接 ,.得到等边三角形 .
任务 .
本作业建议采用等第制评价方式以下评价标准可供参考:
优秀:能证明等边三角形,正确计算等边三角形面积,折纸过程清晰,画图准确,测量准确度高;汇报交流时,内容清晰、交流自信、表达流畅;
良好:能证明等边三角形,正确计算等边三角形面积,折纸过程清晰,画图基本准确,测量准确度较高;汇报交流时,内容清晰、交流自信、表达流畅;
合格:能证明等边三角形,折纸过程清晰,画图达标,测量准确度较高;汇报交流时,内容清晰、交流自信、表达流畅.
22. 平行四边形;;;,
