2.8二次函数的应用--生活中的二次函数
文档属性
| 名称 | 2.8二次函数的应用--生活中的二次函数 |  | |
| 格式 | zip | ||
| 文件大小 | 619.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-04 11:24:09 | ||
图片预览


文档简介
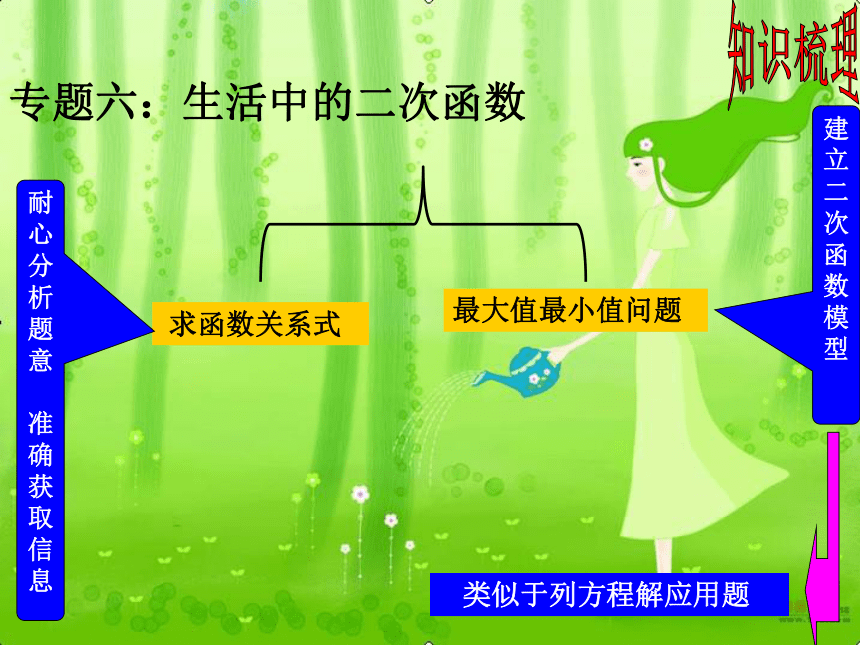
课件16张PPT。义务教育课程标准实验教科书 数学 九年级 (上册) QQ:315743419 二次函数辅导 (六-1)专题六:生活中的二次函数知识梳理建
立
二
次
函
数
模
型 求函数关系式最大值最小值问题 类似于列方程解应用题耐心分析题意
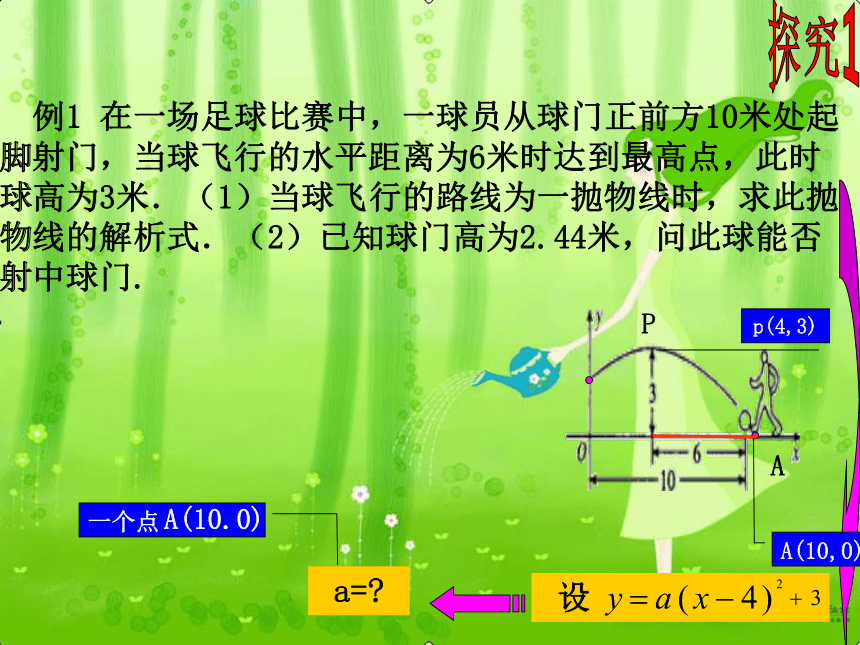
准确获取信息 设 例1 在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.(1)当球飞行的路线为一抛物线时,求此抛物线的解析式.(2)已知球门高为2.44米,问此球能否射中球门.探究1A(10,0) a=?一个点A(10.0)p(4,3)AP 例1 在一场足球比赛中,一球员从球门正前方10米处
起脚射门,当球飞行的水平距离为6米时达到最高点,此
时球高为3米.(1)当球飞行的路线为一抛物线时,求此
抛物线的解析式.(2)已知球门高为2.44米,问此球能
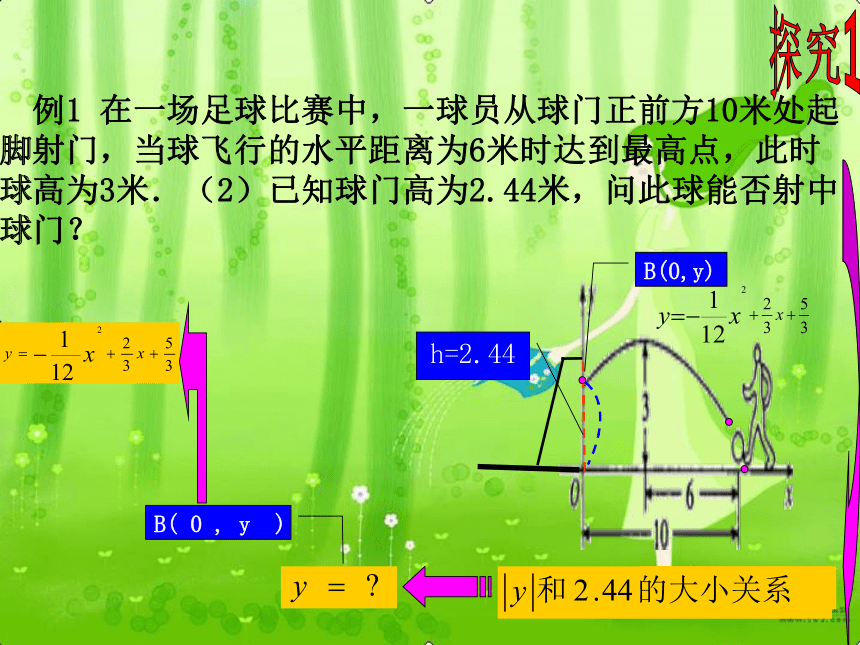
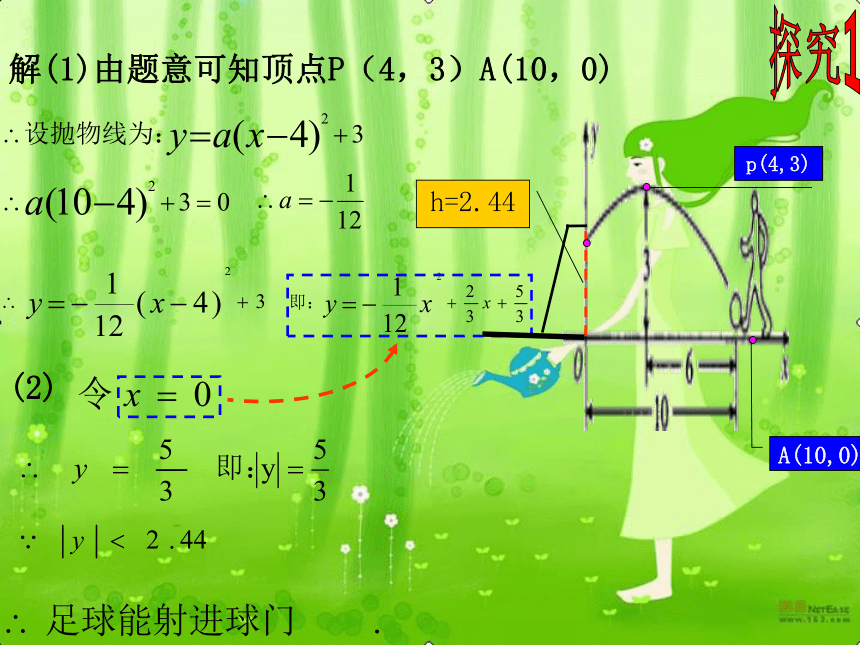
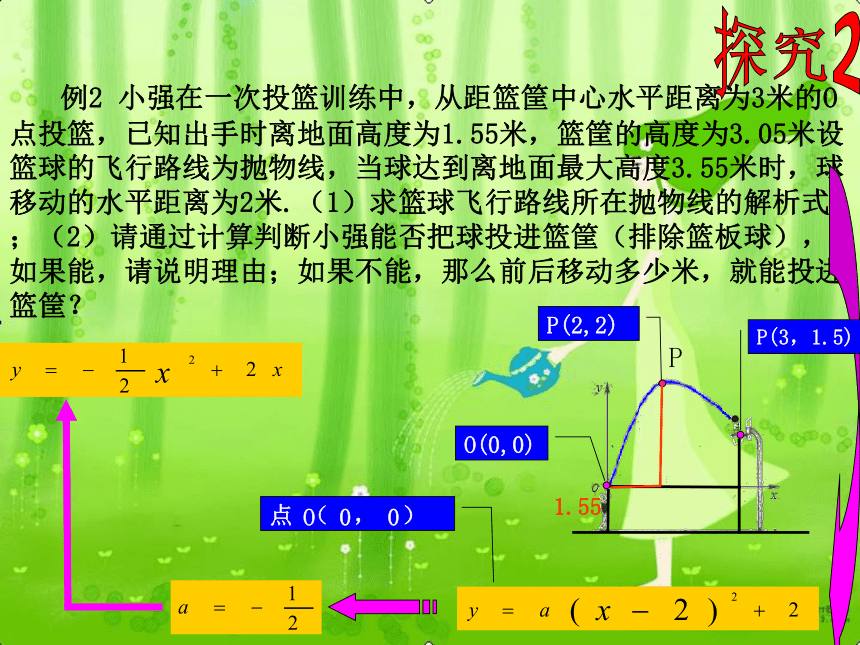
否射中球门.探究1A(10,0)解(1)由题意可知顶点P(4,3)A(10,0)p(4,3)AP 例1 在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.(2)已知球门高为2.44米,问此球能否射中球门?探究1某个数量关系h=2.44B( 0 , y )B(0,y)探究1A(10,0)解(1)由题意可知顶点P(4,3)A(10,0)h=2.44p(4,3)(2)探究2O(0,0)P(2,2) 例2 小强在一次投篮训练中,从距篮筐中心水平距离为3米的O点投篮,已知出手时离地面高度为1.55米,篮筐的高度为3.05米设篮球的飞行路线为抛物线,当球达到离地面最大高度3.55米时,球移动的水平距离为2米.(1)求篮球飞行路线所在抛物线的解析式;(2)请通过计算判断小强能否把球投进篮筐(排除篮板球),如果能,请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?1.55P(3,1.5)点 ( , )O 0 0P探究2O(0,0)P(2,2) 例2 小强在一次投篮训练中,从距篮筐中心水平距离为3米的O点投篮,已知出手时离地面高度为1.55米,篮筐的高度为3.05米设篮球的飞行路线为抛物线,当球达到离地面最大高度3.55米时,球移动的水平距离为2米.(1)求篮球飞行路线所在抛物线的解析式;(2)请通过计算判断小强能否把球投进篮筐(排除篮板球),如果能,请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?1.55P(3,1.5)点 ( , )O 0 0P探究2O(0,0)P(2,2) 例2 小强在一次投篮训练中,从距篮筐中心水平距离为3米的O点投篮,已知出手时离地面高度为1.55米,篮筐的高度为3.05米设篮球的飞行路线为抛物线,当球达到离地面最大高度3.55米时,球移动的水平距离为2米.(1)求篮球飞行路线所在抛物线的解析式;(2)请通过计算判断小强能否把球投进篮筐(排除篮板球),如果能,请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?1.55P(3,1.5)解(1)由题意可知顶点P(2,2)O(0,0)P 例2 请通过计算判断小强能否把球投进篮筐(排除篮板球),请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?(结果可保留根号)探究2A(3,1.5)某个数量关系抛物线是否经过点A(3,1.5)? y=1.5 能投进篮筐(2)把x=3代入 得y=1.5∴此次投篮能投进.点A(3,1.5)是否在抛物线上? 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+2.6.已知球网与O点的水
平距离为9m,高度为2.43m,排球场地长18m (1)求y与x的关系
式;(不要求写出自变量x的取值范围)探究3A(0,2)9mB(9,2.43)(18,0) 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+2.6.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (2)球能否越
过球网?球会不会出界?请说明理由.探究39m某个数量关系排球水平运行9m时的高度与2.43m的大小关系点(9,? )y=2.45B(9,2.43)(18,0) 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (3)若球一定
能越过球网,又不出边界,求h的取值范围.探究3 h的范围 h1方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (3)若球一定
能越过球网,又不出边界,求h的取值范围.探究3B(9,2.43)(18,0)∴ 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (3)若球一定
能越过球网,又不出边界,求h的取值范围.探究3B(9,2.43)(18,0)∴2013.10
立
二
次
函
数
模
型 求函数关系式最大值最小值问题 类似于列方程解应用题耐心分析题意
准确获取信息 设 例1 在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.(1)当球飞行的路线为一抛物线时,求此抛物线的解析式.(2)已知球门高为2.44米,问此球能否射中球门.探究1A(10,0) a=?一个点A(10.0)p(4,3)AP 例1 在一场足球比赛中,一球员从球门正前方10米处
起脚射门,当球飞行的水平距离为6米时达到最高点,此
时球高为3米.(1)当球飞行的路线为一抛物线时,求此
抛物线的解析式.(2)已知球门高为2.44米,问此球能
否射中球门.探究1A(10,0)解(1)由题意可知顶点P(4,3)A(10,0)p(4,3)AP 例1 在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.(2)已知球门高为2.44米,问此球能否射中球门?探究1某个数量关系h=2.44B( 0 , y )B(0,y)探究1A(10,0)解(1)由题意可知顶点P(4,3)A(10,0)h=2.44p(4,3)(2)探究2O(0,0)P(2,2) 例2 小强在一次投篮训练中,从距篮筐中心水平距离为3米的O点投篮,已知出手时离地面高度为1.55米,篮筐的高度为3.05米设篮球的飞行路线为抛物线,当球达到离地面最大高度3.55米时,球移动的水平距离为2米.(1)求篮球飞行路线所在抛物线的解析式;(2)请通过计算判断小强能否把球投进篮筐(排除篮板球),如果能,请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?1.55P(3,1.5)点 ( , )O 0 0P探究2O(0,0)P(2,2) 例2 小强在一次投篮训练中,从距篮筐中心水平距离为3米的O点投篮,已知出手时离地面高度为1.55米,篮筐的高度为3.05米设篮球的飞行路线为抛物线,当球达到离地面最大高度3.55米时,球移动的水平距离为2米.(1)求篮球飞行路线所在抛物线的解析式;(2)请通过计算判断小强能否把球投进篮筐(排除篮板球),如果能,请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?1.55P(3,1.5)点 ( , )O 0 0P探究2O(0,0)P(2,2) 例2 小强在一次投篮训练中,从距篮筐中心水平距离为3米的O点投篮,已知出手时离地面高度为1.55米,篮筐的高度为3.05米设篮球的飞行路线为抛物线,当球达到离地面最大高度3.55米时,球移动的水平距离为2米.(1)求篮球飞行路线所在抛物线的解析式;(2)请通过计算判断小强能否把球投进篮筐(排除篮板球),如果能,请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?1.55P(3,1.5)解(1)由题意可知顶点P(2,2)O(0,0)P 例2 请通过计算判断小强能否把球投进篮筐(排除篮板球),请说明理由;如果不能,那么前后移动多少米,就能投进篮筐?(结果可保留根号)探究2A(3,1.5)某个数量关系抛物线是否经过点A(3,1.5)? y=1.5 能投进篮筐(2)把x=3代入 得y=1.5∴此次投篮能投进.点A(3,1.5)是否在抛物线上? 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+2.6.已知球网与O点的水
平距离为9m,高度为2.43m,排球场地长18m (1)求y与x的关系
式;(不要求写出自变量x的取值范围)探究3A(0,2)9mB(9,2.43)(18,0) 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+2.6.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (2)球能否越
过球网?球会不会出界?请说明理由.探究39m某个数量关系排球水平运行9m时的高度与2.43m的大小关系点(9,? )y=2.45B(9,2.43)(18,0) 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (3)若球一定
能越过球网,又不出边界,求h的取值范围.探究3 h的范围 h1
平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (3)若球一定
能越过球网,又不出边界,求h的取值范围.探究3B(9,2.43)(18,0)∴ 例3 如图,排球运动员站在点O处练习发球,将球从O点正上
方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水
平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的
水平距离为9m,高度为2.43m,排球场地长18m, (3)若球一定
能越过球网,又不出边界,求h的取值范围.探究3B(9,2.43)(18,0)∴2013.10
