5.2.1 基本初等函数的导数 课件(共16张PPT)
文档属性
| 名称 | 5.2.1 基本初等函数的导数 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 627.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-25 00:00:00 | ||
图片预览




文档简介
5.2 导数的运算
5.2.1 基本初等函数的导数
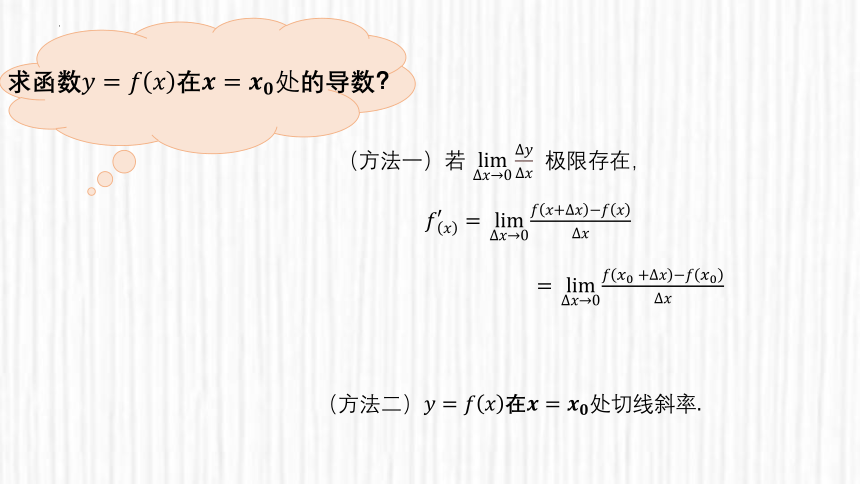
求函数????=????????在????=????????处的导数?
?
(方法一)若 limΔ????→0Δ????Δ???? 极限存在,
????????′=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????????0+Δ?????????????0Δ????
?
(方法二)????=????????在????=????????处切线斜率.
?
根据导数的定义,求函数????=????????的的导数,就是求出当?????→0时,??????????无限趋近的那个定值.
?
下面我们来求几个常用函数的导数
1. 函数 ????=????????=???? 的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0?????????Δ????
?
????????′=limΔ????→0Δ????Δ????
?
= 0
2. 函数????=????????=????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????+??????????Δ????
?
????????′=limΔ????→0Δ????Δ????
?
= 1
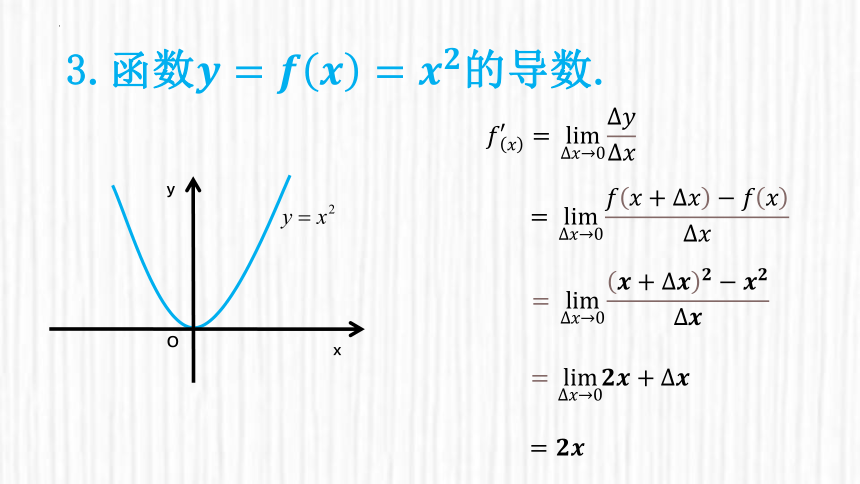
3.函数????=????????=????????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????+???????????????????????
?
????????′=limΔ????→0Δ????Δ????
?
=????????
?
=limΔ????→0????????+?????
?
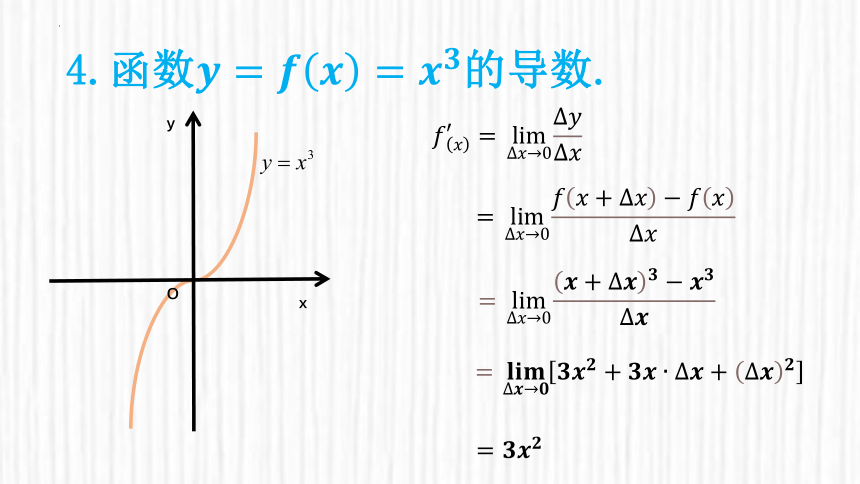
4.函数????=????????=????????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????+???????????????????????
?
????????′=limΔ????→0Δ????Δ????
?
=????????????
?
=?????????????????→????????????????+??????????????+?????????
?
5.函数????=????????=????????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????????+???????????????????
?
????????′=limΔ????→0Δ????Δ????
?
=?????????????
?
6.函数????=????????=????的导数.
?
x
O
y
=limΔ????→0????+????????????????
?
=limΔ????→0????+??????????????+?????+?????????????+?????+??
?
????????′=limΔ????→0Δ????Δ????
?
=?????????????????→01????+?????+????
?
=12????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 原函数
导函数
f(x)=C(C为常数)
f'(x)=0
f(x)=xα(α∈Q,α≠0)
f'(x)= ?????????????1
f(x)=sin x
f'(x)= ????????????????
f(x)=cos x
f'(x)= ?????????????????
f(x)=ax(a>0,且a≠1)
f'(x)= ??????????????????????(????>0,????≠1)
f(x)=ex
f'(x)= ????????
f(x)=logax(a>0,且a≠1)
f'(x)= 1?????????????????(????>0,????≠1)
f(x)=ln x
f'(x)=1????
基本初等函数的导数
例1 求下列函数的导数:
解:
练习 1.求下列函数的导数:
解:
练习 2.求下列函数在给定处的导数:
解:
例2 已知曲线 , (1)求曲线在点M(1,1)处的切线方程;
(2)求过点N(1,0)的曲线的切线方程.
解:
∵y=1???? ,∴????′=?1????2 .
(1)显然M(1,1)是曲线上的点,所以M为切点,所求切线斜率k=f′(1)=-1.
所以曲线在P(1,1)处的切线方程为y-1=-(x-1),即为x+y-2=0.
?
(2)显然N(1,0)不是曲线上的点,设过该点的切线的切点为A(a,1????),
那么该切线斜率为k=f′(a)=?1????2
则切线方程为y-1????=-1????2(x-a) ①
将N(1,0)代入方程:0-1????=-1????2(1-a).
得a=12,代入方程①整理可得切线方程为y=-4x+4.
?
课堂练习
1.函数????=4????2在x=2处的导数为________.
?
2.若y=cos2????3,则y′=________.
?
3.设函数f(x)=log????????,f′(1)=-1,则a=________.
?
4.曲线 在点(4,2)处的切线方程为______________.
5.点P是函数????=????????上一点,则P到直线y=x的最小距离为_______.
?
-1
0
????????
?
?????????????+????=????
?
????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 原函数
导函数
f(x)=C(C为常数)
f'(x)=
f(x)=xα(α∈Q,α≠0)
f'(x)=
f(x)=sin x
f'(x)=
f(x)=cos x
f'(x)=
f(x)=ax(a>0,且a≠1)
f'(x)= ?
(????>0,????≠1)
f(x)=ex
f'(x)=
f(x)=logax(a>0,且a≠1)
f'(x)=
?(????>0,????≠1)
f(x)=ln x
f'(x)=
总结
5.2.1 基本初等函数的导数
求函数????=????????在????=????????处的导数?
?
(方法一)若 limΔ????→0Δ????Δ???? 极限存在,
????????′=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????????0+Δ?????????????0Δ????
?
(方法二)????=????????在????=????????处切线斜率.
?
根据导数的定义,求函数????=????????的的导数,就是求出当?????→0时,??????????无限趋近的那个定值.
?
下面我们来求几个常用函数的导数
1. 函数 ????=????????=???? 的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0?????????Δ????
?
????????′=limΔ????→0Δ????Δ????
?
= 0
2. 函数????=????????=????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????+??????????Δ????
?
????????′=limΔ????→0Δ????Δ????
?
= 1
3.函数????=????????=????????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????+???????????????????????
?
????????′=limΔ????→0Δ????Δ????
?
=????????
?
=limΔ????→0????????+?????
?
4.函数????=????????=????????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????+???????????????????????
?
????????′=limΔ????→0Δ????Δ????
?
=????????????
?
=?????????????????→????????????????+??????????????+?????????
?
5.函数????=????????=????????的导数.
?
x
O
y
=limΔ????→0????????+Δ?????????????Δ????
?
=limΔ????→0????????+???????????????????
?
????????′=limΔ????→0Δ????Δ????
?
=?????????????
?
6.函数????=????????=????的导数.
?
x
O
y
=limΔ????→0????+????????????????
?
=limΔ????→0????+??????????????+?????+?????????????+?????+??
?
????????′=limΔ????→0Δ????Δ????
?
=?????????????????→01????+?????+????
?
=12????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 原函数
导函数
f(x)=C(C为常数)
f'(x)=0
f(x)=xα(α∈Q,α≠0)
f'(x)= ?????????????1
f(x)=sin x
f'(x)= ????????????????
f(x)=cos x
f'(x)= ?????????????????
f(x)=ax(a>0,且a≠1)
f'(x)= ??????????????????????(????>0,????≠1)
f(x)=ex
f'(x)= ????????
f(x)=logax(a>0,且a≠1)
f'(x)= 1?????????????????(????>0,????≠1)
f(x)=ln x
f'(x)=1????
基本初等函数的导数
例1 求下列函数的导数:
解:
练习 1.求下列函数的导数:
解:
练习 2.求下列函数在给定处的导数:
解:
例2 已知曲线 , (1)求曲线在点M(1,1)处的切线方程;
(2)求过点N(1,0)的曲线的切线方程.
解:
∵y=1???? ,∴????′=?1????2 .
(1)显然M(1,1)是曲线上的点,所以M为切点,所求切线斜率k=f′(1)=-1.
所以曲线在P(1,1)处的切线方程为y-1=-(x-1),即为x+y-2=0.
?
(2)显然N(1,0)不是曲线上的点,设过该点的切线的切点为A(a,1????),
那么该切线斜率为k=f′(a)=?1????2
则切线方程为y-1????=-1????2(x-a) ①
将N(1,0)代入方程:0-1????=-1????2(1-a).
得a=12,代入方程①整理可得切线方程为y=-4x+4.
?
课堂练习
1.函数????=4????2在x=2处的导数为________.
?
2.若y=cos2????3,则y′=________.
?
3.设函数f(x)=log????????,f′(1)=-1,则a=________.
?
4.曲线 在点(4,2)处的切线方程为______________.
5.点P是函数????=????????上一点,则P到直线y=x的最小距离为_______.
?
-1
0
????????
?
?????????????+????=????
?
????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 原函数
导函数
f(x)=C(C为常数)
f'(x)=
f(x)=xα(α∈Q,α≠0)
f'(x)=
f(x)=sin x
f'(x)=
f(x)=cos x
f'(x)=
f(x)=ax(a>0,且a≠1)
f'(x)= ?
(????>0,????≠1)
f(x)=ex
f'(x)=
f(x)=logax(a>0,且a≠1)
f'(x)=
?(????>0,????≠1)
f(x)=ln x
f'(x)=
总结
