人教版小学数学五年级上册8.1《位置、可能性、植树问题 复习》课件(共19张PPT)
文档属性
| 名称 | 人教版小学数学五年级上册8.1《位置、可能性、植树问题 复习》课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-25 22:43:21 | ||
图片预览

文档简介
(共19张PPT)
位置、可能性、植树问题
R·五年级上册
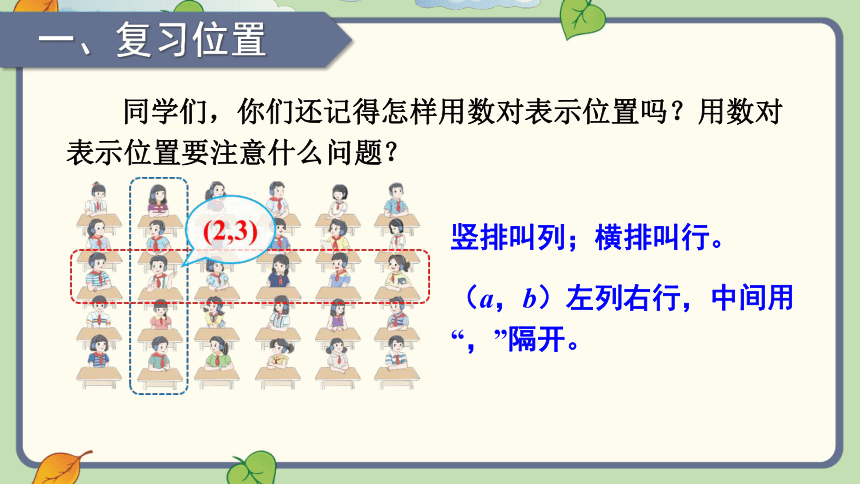
同学们,你们还记得怎样用数对表示位置吗?用数对表示位置要注意什么问题?
竖排叫列;横排叫行。
(a,b)左列右行,中间用“,”隔开。
一、复习位置
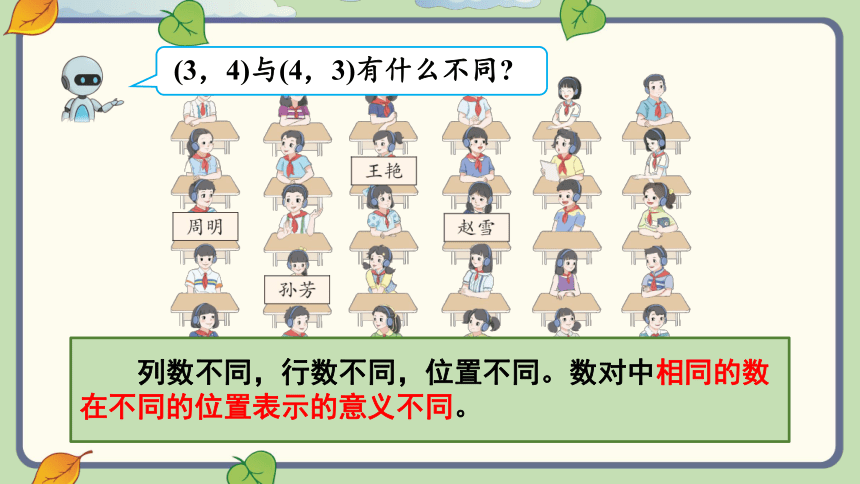
(3,4)与(4,3)有什么不同
列数不同,行数不同,位置不同。数对中相同的数在不同的位置表示的意义不同。
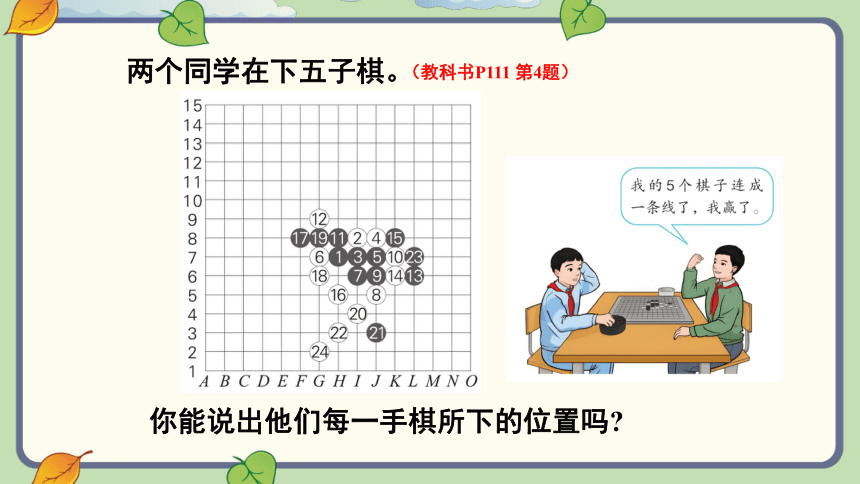
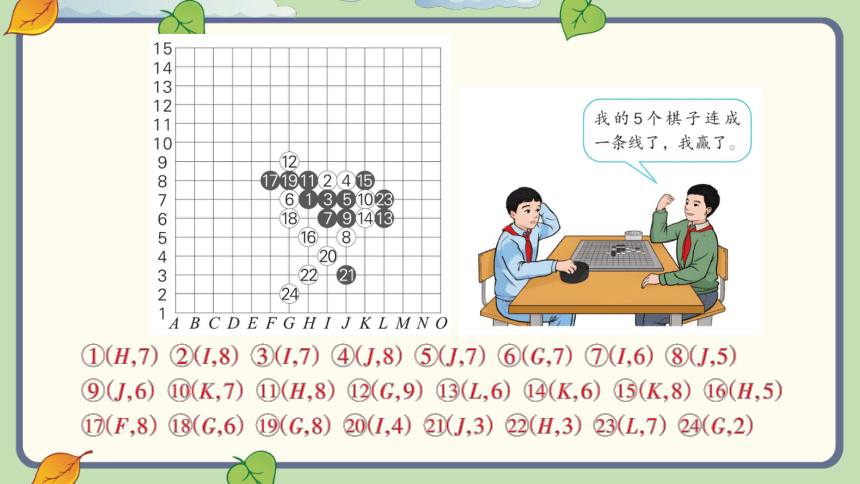
两个同学在下五子棋。
(教科书P111 第4题)
你能说出他们每一手棋所下的位置吗
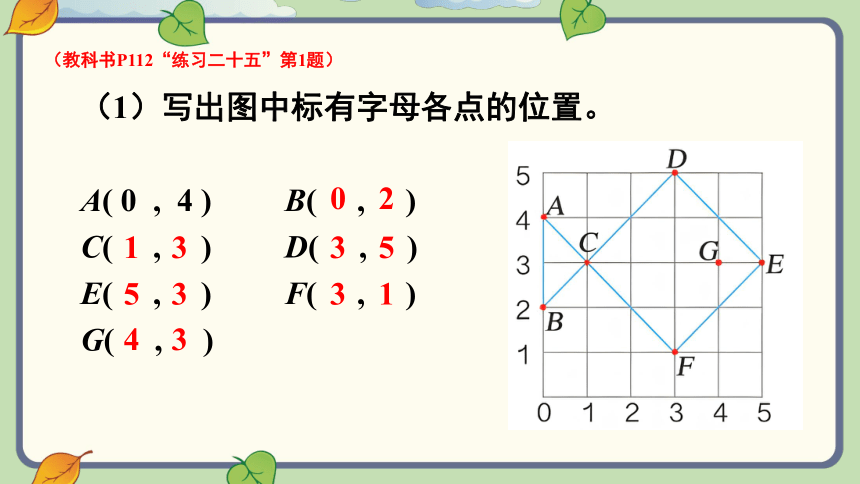
(1)写出图中标有字母各点的位置。
A( 0 , 4 ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , )
0 2
1 3
3 5
5 3
3 1
4 3
(教科书P112“练习二十五”第1题)
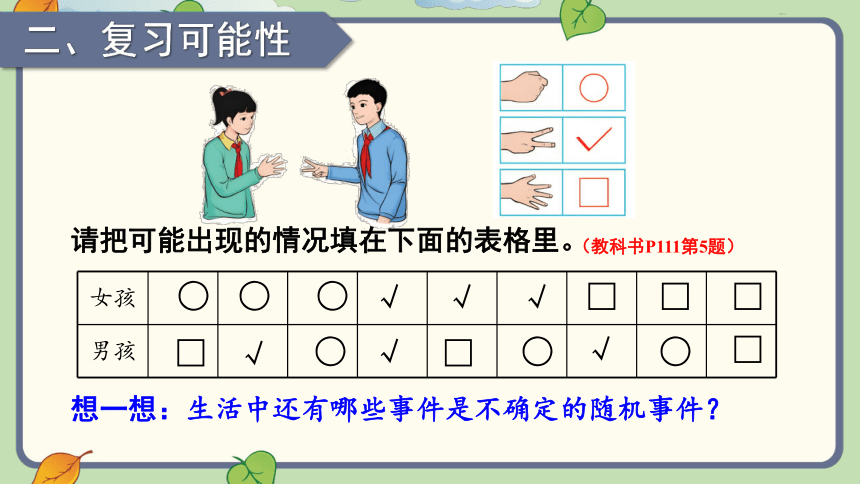
请把可能出现的情况填在下面的表格里。
女孩
男孩
○
√
□
○
○
○
√
√
√
√
□
○
□
□
□
√
○
□
(教科书P111第5题)
二、复习可能性
想一想:生活中还有哪些事件是不确定的随机事件?
在下面的每个转盘中,指针停在哪种颜色区域的可能性最大 停在哪种颜色区域的可能性最小
指针停在蓝色区域的可能性最大,停在黄色区域的可能性最小。
指针停在红色区域的可能性最大,停在蓝色区域的可能性最小。
(教科书P114“练习二十五”第11题)
两个都是正面,两个都是反面,
一个正面一个反面。
(P114“练习二十五”第12题)
常见类型:
①两端都栽的植树问题;
②两端都不栽的植树问题;
③一端栽、一端不栽的植树问题;
④封闭图形的植树问题。
三、复习植树问题
5 个手指有几个空隙?
间隔
在数学上,我们把像这样的空叫做间隔。
5 个手指有 4 个间隔。
新课导入
例:同学们在长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
100 m 太长了,可以先用简单的数试试。
应该栽5棵,直接用除法计算不对。
5 m
20 m
5 m
5 m
5 m
20÷5=4(棵)
自己选一些长度试一试,看看有什么规律。
5 m
25 m
5 m
5 m
5 m
5 m
距离(米) 间隔数(个) 棵数(棵)
20
25
30
35
4
5
5
6
6
7
7
8
总路长÷间隔长=间隔数
棵数 = 间隔数+1(两端都栽)
在全长20 m的小路上植树,每隔5 m栽一棵,你能想出几种植树方案?
特点 间隔数 棵数 与间隔数的关系
方案1 两端都栽
方案2 两端都不栽
方案3 一端栽,一端不栽
方案4 封闭图形
4
5
棵数=间隔数+1
4
3
棵数=间隔数-1
4
4
棵数=间隔数
4
4
棵数=间隔数
(1)在一条长400 m的道路一旁安装路灯,每隔50 m安装一座(两端都要安装),一共可以安装多少座路灯?
400÷50=8
间隔数:
8+1=9(座)
可以安装:
答:一共可以安装9座路灯。
(2)两座楼房之间相距56 m,每隔4 m栽雪松一棵,一行能栽多少棵?
56÷4=14
间隔数:
14-1=13(棵)
能栽树:
答:一行能栽13棵。
(3)一个圆形池塘,它的周长是200 m,每隔10 m栽一棵柳树,需要树苗多少棵?
200÷10=20(棵)
间隔数:
答:需要20棵树苗。
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
位置、可能性、植树问题
R·五年级上册
同学们,你们还记得怎样用数对表示位置吗?用数对表示位置要注意什么问题?
竖排叫列;横排叫行。
(a,b)左列右行,中间用“,”隔开。
一、复习位置
(3,4)与(4,3)有什么不同
列数不同,行数不同,位置不同。数对中相同的数在不同的位置表示的意义不同。
两个同学在下五子棋。
(教科书P111 第4题)
你能说出他们每一手棋所下的位置吗
(1)写出图中标有字母各点的位置。
A( 0 , 4 ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , )
0 2
1 3
3 5
5 3
3 1
4 3
(教科书P112“练习二十五”第1题)
请把可能出现的情况填在下面的表格里。
女孩
男孩
○
√
□
○
○
○
√
√
√
√
□
○
□
□
□
√
○
□
(教科书P111第5题)
二、复习可能性
想一想:生活中还有哪些事件是不确定的随机事件?
在下面的每个转盘中,指针停在哪种颜色区域的可能性最大 停在哪种颜色区域的可能性最小
指针停在蓝色区域的可能性最大,停在黄色区域的可能性最小。
指针停在红色区域的可能性最大,停在蓝色区域的可能性最小。
(教科书P114“练习二十五”第11题)
两个都是正面,两个都是反面,
一个正面一个反面。
(P114“练习二十五”第12题)
常见类型:
①两端都栽的植树问题;
②两端都不栽的植树问题;
③一端栽、一端不栽的植树问题;
④封闭图形的植树问题。
三、复习植树问题
5 个手指有几个空隙?
间隔
在数学上,我们把像这样的空叫做间隔。
5 个手指有 4 个间隔。
新课导入
例:同学们在长 100 m 的小路一边植树,每隔 5 m 栽一棵(两端要栽)。一共要栽多少棵树?
100 m 太长了,可以先用简单的数试试。
应该栽5棵,直接用除法计算不对。
5 m
20 m
5 m
5 m
5 m
20÷5=4(棵)
自己选一些长度试一试,看看有什么规律。
5 m
25 m
5 m
5 m
5 m
5 m
距离(米) 间隔数(个) 棵数(棵)
20
25
30
35
4
5
5
6
6
7
7
8
总路长÷间隔长=间隔数
棵数 = 间隔数+1(两端都栽)
在全长20 m的小路上植树,每隔5 m栽一棵,你能想出几种植树方案?
特点 间隔数 棵数 与间隔数的关系
方案1 两端都栽
方案2 两端都不栽
方案3 一端栽,一端不栽
方案4 封闭图形
4
5
棵数=间隔数+1
4
3
棵数=间隔数-1
4
4
棵数=间隔数
4
4
棵数=间隔数
(1)在一条长400 m的道路一旁安装路灯,每隔50 m安装一座(两端都要安装),一共可以安装多少座路灯?
400÷50=8
间隔数:
8+1=9(座)
可以安装:
答:一共可以安装9座路灯。
(2)两座楼房之间相距56 m,每隔4 m栽雪松一棵,一行能栽多少棵?
56÷4=14
间隔数:
14-1=13(棵)
能栽树:
答:一行能栽13棵。
(3)一个圆形池塘,它的周长是200 m,每隔10 m栽一棵柳树,需要树苗多少棵?
200÷10=20(棵)
间隔数:
答:需要20棵树苗。
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
