17.5 实践与探索 课件(共29张PPT)
文档属性
| 名称 | 17.5 实践与探索 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 08:50:07 | ||
图片预览





文档简介
(共29张PPT)
17.5 实践与探索
华师大版 八年级 下册
教学目标
教学目标:1.能根据一次函数的图象求二元一次方程组的解.
2.能通过数形结合说出一次函数与一元一次方程及一元一次
不等式的联系.
3.会图象上获取信息的能力,利用数形结合解决实际问题.
教学重点:利用一次函数的图象解方程组、不等式,利用函数图象性质
解决问题.
教学难点:从函数的图象中提炼出有用的信息,选择恰当的函数图象、
性质解决问题.
新知导入
情境引入
在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用.
新知讲解
合作学习
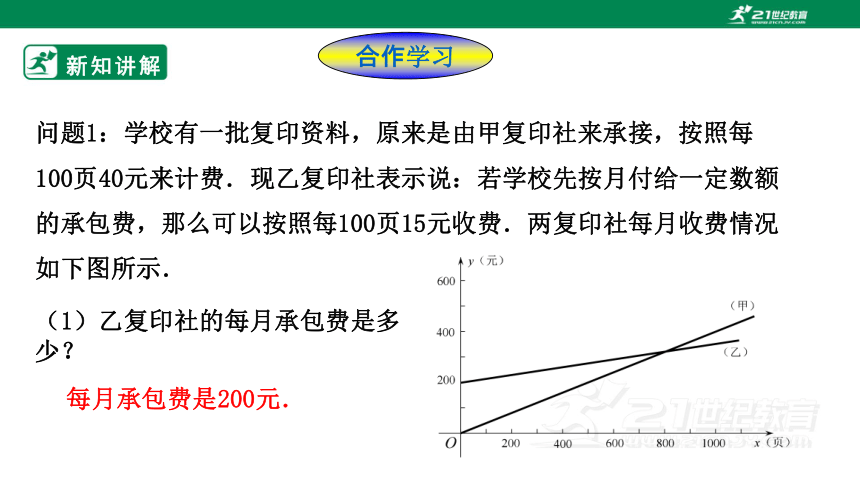
问题1:学校有一批复印资料,原来是由甲复印社来承接,按照每100页40元来计费.现乙复印社表示说:若学校先按月付给一定数额的承包费,那么可以按照每100页15元收费.两复印社每月收费情况如下图所示.
(1)乙复印社的每月承包费是多少?
每月承包费是200元.
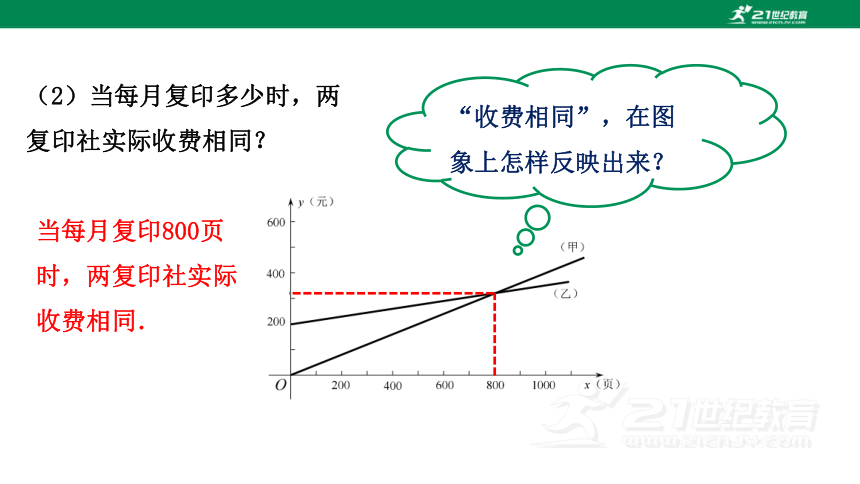
(2)当每月复印多少时,两复印社实际收费相同?
“收费相同”,在图象上怎样反映出来?
当每月复印800页时,两复印社实际收费相同.
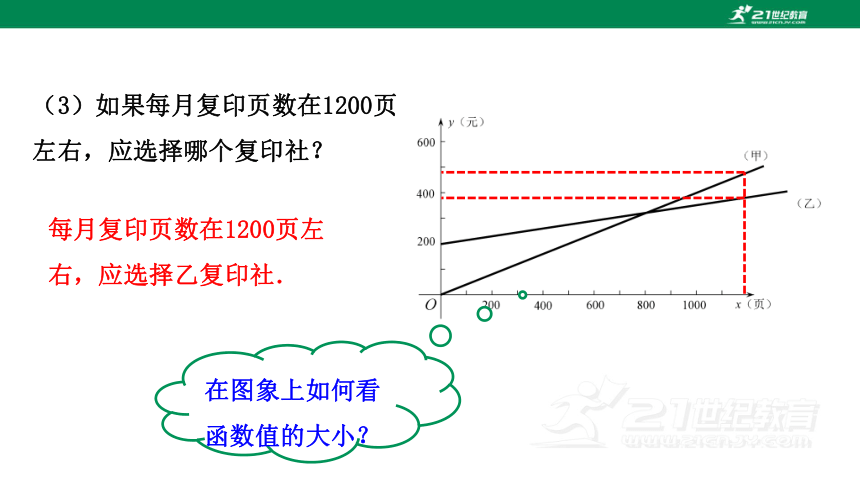
(3)如果每月复印页数在1200页左右,应选择哪个复印社?
每月复印页数在1200页左右,应选择乙复印社.
在图象上如何看函数值的大小?
思考
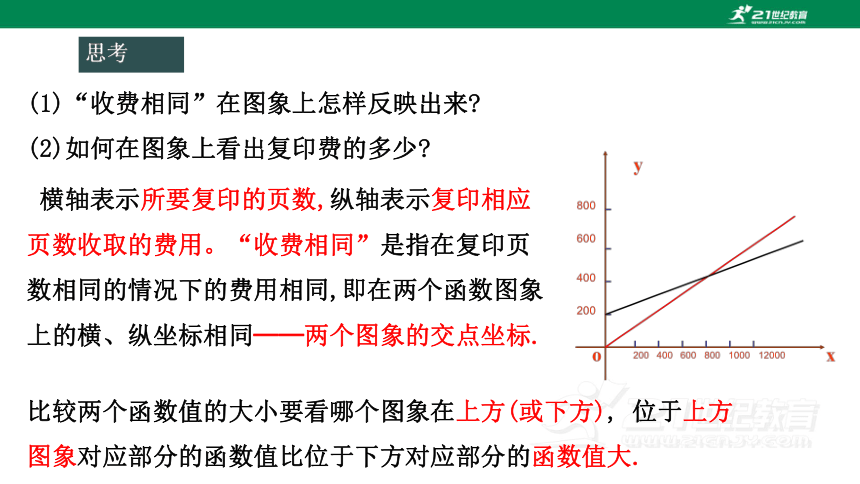
(1)“收费相同”在图象上怎样反映出来
(2)如何在图象上看出复印费的多少
横轴表示所要复印的页数,纵轴表示复印相应页数收取的费用。“收费相同”是指在复印页数相同的情况下的费用相同,即在两个函数图象上的横、纵坐标相同──两个图象的交点坐标.
比较两个函数值的大小要看哪个图象在上方(或下方), 位于上方图象对应部分的函数值比位于下方对应部分的函数值大.
提炼概念
由函数图象解答问题时,首先要明确横、纵轴表示的含义, 函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定取值范围内,位于上方图象的函数值要比位于下方图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确, 观察得越仔细,所得的值就越准确.
二元一次方程 x+y=3 可改写成一次函数y=3-x.以方程 x+y=3 的解为坐标的所有点组成的图象就是 一次函数 y=3-x 的图象.
两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而这两个关系式可以看成关于x、y的两个方程,所以交点的坐标就是这两个方程组成的方程组的解.
典例精讲
例 利用一次函数的图象,求二元一次方程组 的解.
分析 方程组中第一个方程已经是一次函数的形式,第二个方程可变形为一次函数的形式: .
解: 在直角坐标系中分别作出一次函数y=x+5和 ,如下图所示.
因为两条直线的交点坐标是( - 4,1),所以方程组的解为 .
一次函数与二元一次方程(组)
1.一次函数与二元一次方程的关系:
每对函数值都是方程的一组解
一次函数
函数角度
方程角度
二元一次方程
2.一次函数与二元一次方程(组)的关系:
交点
解
问题2:画出函数y=的图象,根据图象,说明:
(1)x取什么值时,函数值y等于零?
(2)x取什么值时,函数值y大于零?
解:有图象可知:(1)当x=-2时,y等于0.
(2)当x>-2时,y大于0.
(1)一元一次方程的解与函数y=的图象有什么关系?
(2)一元一次方程的解,不等式的解集与函数 的图象有 什么关系?
思考
从“数”的角度来看,一次函数y=kx+b(k≠0)的函数值是0时,对应的x的值就是一元一次方程 kx+b=0的解;当一次函数y=kx+b的值大于0时,对应部分x的取值的集合,就是不等式 kx+b>0的解集;当一次函数y=kx+b的值小于0时,对应部分x的取值的集合,就是不等式 kx+b<0的解集.
从“形”的角度看,直线 y=kx+b(k≠0)与x轴交点的横坐标就是方程 kx+b=0的解;直线 y=kx+b位于x轴上方部分对应的x的值的集合就是不等式 kx+b>0的解集;直线 y=kx+b位于x轴下方部分对应的x的值的集合就是不等式 kx+b<0的解集.
归纳总结
问题3:为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系
t(℃) -40 -20 -10 0 10 20 40 60
V(cm3) 998.3 999.2 999.6 1000 1 000.3 1 000.7 1 001.6 1 002.3
分析:在平面直角坐标系中将这些数值所对应的点在坐标系中描出.我们发现,这些点大致位于一条直线上,可知V和t近似地符合一次函数关系.
解:设V和t的函数关系式是V =kt +b(k≠0)根据题意,得
,解得 .
所以V与t的函数关系式可能是: V =0.04t+999.9.
归纳概念
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实 生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
课堂练习
1.如图,一次函数y1=k1x+b1与y2=k2x+b2的图象相交于A(3,2),则不等式k2x+b2>k1x+b1的解集为_________.
x<3
2.用图象法解方程组
3.画出函数y=2x+6的图象,利用图象:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解;
(3)若 2≤y≤2求x的取值范围.
解:图象为:
(1)观察图象知:该函数图象经过点 ( 3,0),
故方程2x+6=0的解为x= 3;
(2)观察图象知:当x> 3时,y>0,
故不等式2x+6>0的解为x> 3;
(3)当 2≤y≤2时, 4≤x≤ 2.
4.如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2= x 2与坐标轴交于B、D两点,两线的交点为P点.
(1)求△APB的面积;
(2)利用图象求当x取何值时,y1解:(1)联立l1、 l2 .解得 .
∴P点坐标为(-1,-1),
又∵A(0,1),B(0,-2),
∴ .
(2)由图可知,当x< 1时,y15.小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗
(2)问43码的鞋相当于多少厘米的鞋
x(厘米) 23 23.5 24.5 25.5 26 ……
y(码) 36 37 39 41 42 ……
把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
x (厘米)
y(码)
23
23.5
24
O
40
36
41
37
38
39
24.5
25.5
25
26
26.5
27
42
解:(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
根据题意,得
所以y与x的函数关系式可能是:y=2x-10
(2)当y=43时,2x-10=43,
解得x=26.5.
课堂总结
求实际问题中的函数关系式的基本方法:
一是找_____________建立函数关系式,基本步骤如下:
(1)审清题意; (2)找准相等关系; (3)确定自变量和因变量,选用适当的字母表示;
相等关系
(4)列出相关数量的关系式表示相等关系; (5)写出关系式.
二是用______________,基本步骤如下:
(1)设出待求的函数关系式; (2)把已知条件代入函数关系式,得到方程或方程组;
(3)解方程或方程组,求出待定系数的值;(4)写出函数关系式.
待定系数法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.5 实践与探索
华师大版 八年级 下册
教学目标
教学目标:1.能根据一次函数的图象求二元一次方程组的解.
2.能通过数形结合说出一次函数与一元一次方程及一元一次
不等式的联系.
3.会图象上获取信息的能力,利用数形结合解决实际问题.
教学重点:利用一次函数的图象解方程组、不等式,利用函数图象性质
解决问题.
教学难点:从函数的图象中提炼出有用的信息,选择恰当的函数图象、
性质解决问题.
新知导入
情境引入
在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用.
新知讲解
合作学习
问题1:学校有一批复印资料,原来是由甲复印社来承接,按照每100页40元来计费.现乙复印社表示说:若学校先按月付给一定数额的承包费,那么可以按照每100页15元收费.两复印社每月收费情况如下图所示.
(1)乙复印社的每月承包费是多少?
每月承包费是200元.
(2)当每月复印多少时,两复印社实际收费相同?
“收费相同”,在图象上怎样反映出来?
当每月复印800页时,两复印社实际收费相同.
(3)如果每月复印页数在1200页左右,应选择哪个复印社?
每月复印页数在1200页左右,应选择乙复印社.
在图象上如何看函数值的大小?
思考
(1)“收费相同”在图象上怎样反映出来
(2)如何在图象上看出复印费的多少
横轴表示所要复印的页数,纵轴表示复印相应页数收取的费用。“收费相同”是指在复印页数相同的情况下的费用相同,即在两个函数图象上的横、纵坐标相同──两个图象的交点坐标.
比较两个函数值的大小要看哪个图象在上方(或下方), 位于上方图象对应部分的函数值比位于下方对应部分的函数值大.
提炼概念
由函数图象解答问题时,首先要明确横、纵轴表示的含义, 函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定取值范围内,位于上方图象的函数值要比位于下方图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确, 观察得越仔细,所得的值就越准确.
二元一次方程 x+y=3 可改写成一次函数y=3-x.以方程 x+y=3 的解为坐标的所有点组成的图象就是 一次函数 y=3-x 的图象.
两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而这两个关系式可以看成关于x、y的两个方程,所以交点的坐标就是这两个方程组成的方程组的解.
典例精讲
例 利用一次函数的图象,求二元一次方程组 的解.
分析 方程组中第一个方程已经是一次函数的形式,第二个方程可变形为一次函数的形式: .
解: 在直角坐标系中分别作出一次函数y=x+5和 ,如下图所示.
因为两条直线的交点坐标是( - 4,1),所以方程组的解为 .
一次函数与二元一次方程(组)
1.一次函数与二元一次方程的关系:
每对函数值都是方程的一组解
一次函数
函数角度
方程角度
二元一次方程
2.一次函数与二元一次方程(组)的关系:
交点
解
问题2:画出函数y=的图象,根据图象,说明:
(1)x取什么值时,函数值y等于零?
(2)x取什么值时,函数值y大于零?
解:有图象可知:(1)当x=-2时,y等于0.
(2)当x>-2时,y大于0.
(1)一元一次方程的解与函数y=的图象有什么关系?
(2)一元一次方程的解,不等式的解集与函数 的图象有 什么关系?
思考
从“数”的角度来看,一次函数y=kx+b(k≠0)的函数值是0时,对应的x的值就是一元一次方程 kx+b=0的解;当一次函数y=kx+b的值大于0时,对应部分x的取值的集合,就是不等式 kx+b>0的解集;当一次函数y=kx+b的值小于0时,对应部分x的取值的集合,就是不等式 kx+b<0的解集.
从“形”的角度看,直线 y=kx+b(k≠0)与x轴交点的横坐标就是方程 kx+b=0的解;直线 y=kx+b位于x轴上方部分对应的x的值的集合就是不等式 kx+b>0的解集;直线 y=kx+b位于x轴下方部分对应的x的值的集合就是不等式 kx+b<0的解集.
归纳总结
问题3:为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系
t(℃) -40 -20 -10 0 10 20 40 60
V(cm3) 998.3 999.2 999.6 1000 1 000.3 1 000.7 1 001.6 1 002.3
分析:在平面直角坐标系中将这些数值所对应的点在坐标系中描出.我们发现,这些点大致位于一条直线上,可知V和t近似地符合一次函数关系.
解:设V和t的函数关系式是V =kt +b(k≠0)根据题意,得
,解得 .
所以V与t的函数关系式可能是: V =0.04t+999.9.
归纳概念
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实 生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
课堂练习
1.如图,一次函数y1=k1x+b1与y2=k2x+b2的图象相交于A(3,2),则不等式k2x+b2>k1x+b1的解集为_________.
x<3
2.用图象法解方程组
3.画出函数y=2x+6的图象,利用图象:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解;
(3)若 2≤y≤2求x的取值范围.
解:图象为:
(1)观察图象知:该函数图象经过点 ( 3,0),
故方程2x+6=0的解为x= 3;
(2)观察图象知:当x> 3时,y>0,
故不等式2x+6>0的解为x> 3;
(3)当 2≤y≤2时, 4≤x≤ 2.
4.如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2= x 2与坐标轴交于B、D两点,两线的交点为P点.
(1)求△APB的面积;
(2)利用图象求当x取何值时,y1
∴P点坐标为(-1,-1),
又∵A(0,1),B(0,-2),
∴ .
(2)由图可知,当x< 1时,y1
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗
(2)问43码的鞋相当于多少厘米的鞋
x(厘米) 23 23.5 24.5 25.5 26 ……
y(码) 36 37 39 41 42 ……
把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
x (厘米)
y(码)
23
23.5
24
O
40
36
41
37
38
39
24.5
25.5
25
26
26.5
27
42
解:(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
根据题意,得
所以y与x的函数关系式可能是:y=2x-10
(2)当y=43时,2x-10=43,
解得x=26.5.
课堂总结
求实际问题中的函数关系式的基本方法:
一是找_____________建立函数关系式,基本步骤如下:
(1)审清题意; (2)找准相等关系; (3)确定自变量和因变量,选用适当的字母表示;
相等关系
(4)列出相关数量的关系式表示相等关系; (5)写出关系式.
二是用______________,基本步骤如下:
(1)设出待求的函数关系式; (2)把已知条件代入函数关系式,得到方程或方程组;
(3)解方程或方程组,求出待定系数的值;(4)写出函数关系式.
待定系数法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
