2022-2023学年北师大版数学九年级下册3.4圆周角和圆心角的关系 同步培优训练(含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学九年级下册3.4圆周角和圆心角的关系 同步培优训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 08:14:20 | ||
图片预览


文档简介
北师大版数学九年级下册 3.4圆周角和圆心角的关系 同步培优训练
一、单选题
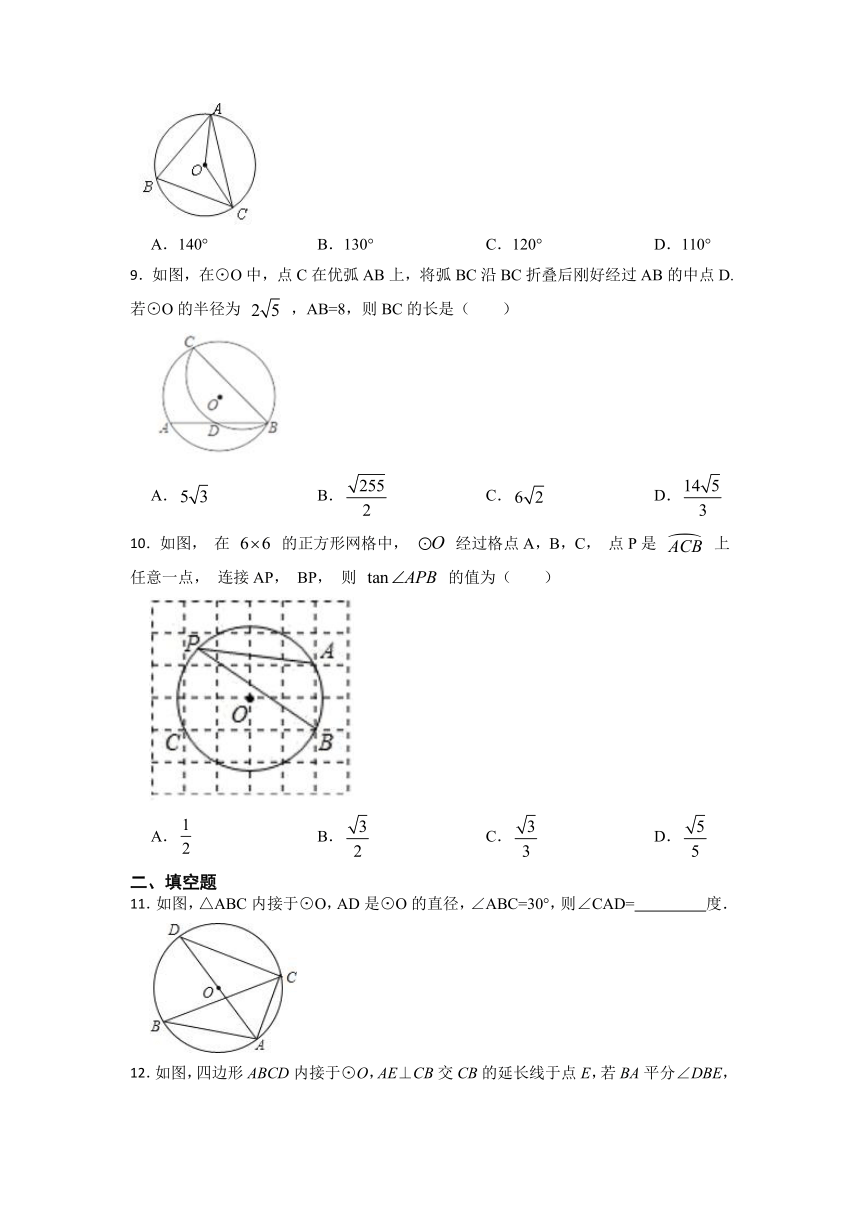
1.如图,已知A,B,C在⊙O上, 的度数为300°,∠C的度数是( )
A.30° B.40° C.50° D.60°
2.如图,四边形ABCD为⊙O的内接四边形,若∠BCD=110°,则∠BAD为( )
A.140° B.110° C.90° D.70°
3.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=36°,那么∠BAD等于( ).
A.36° B.44° C.54° D.56°
4.如图,在平面直角坐标系中,点爿是双曲线y= 上的一点,以点爿为圆心,0A为半径画圆。交两坐标轴于点B,C.若OB=8,则OC的长为( )
A.2 B.4 C.2 D.6
5.有一直径为的圆,且圆上有、、、四点,其位置如图所示.若,,,,,则下列弧长关系何者正确?( )
A.,
B.,
C.,
D.,
6.如图,已知 是半圆O的直径,弦 相交于点P,若 ,则 的值( )
A. B. C. D.
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
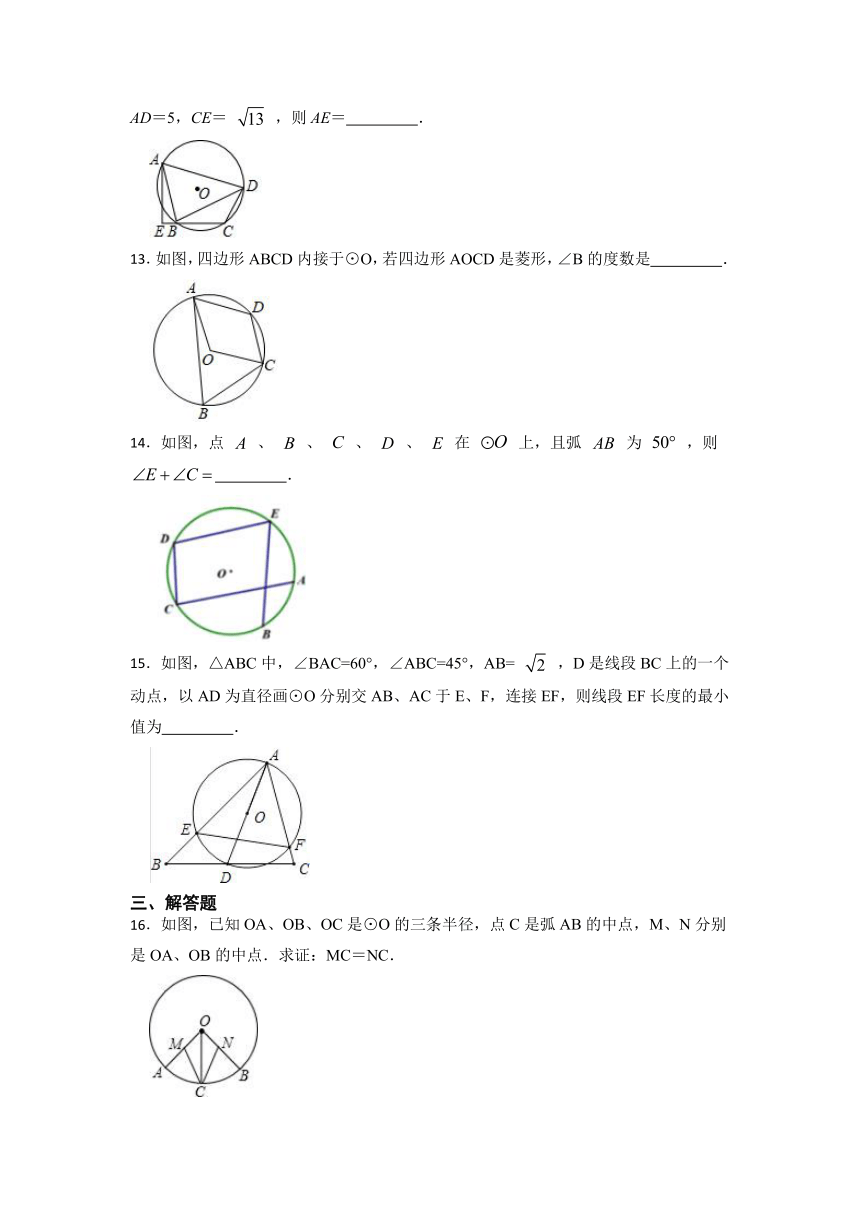
8.如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的度数为( )
A.140° B.130° C.120° D.110°
9.如图,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为 ,AB=8,则BC的长是( )
A. B. C. D.
10.如图, 在 的正方形网格中, 经过格点A,B,C, 点P是 上任意一点, 连接AP, BP, 则 的值为( )
A. B. C. D.
二、填空题
11.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=30°,则∠CAD= 度.
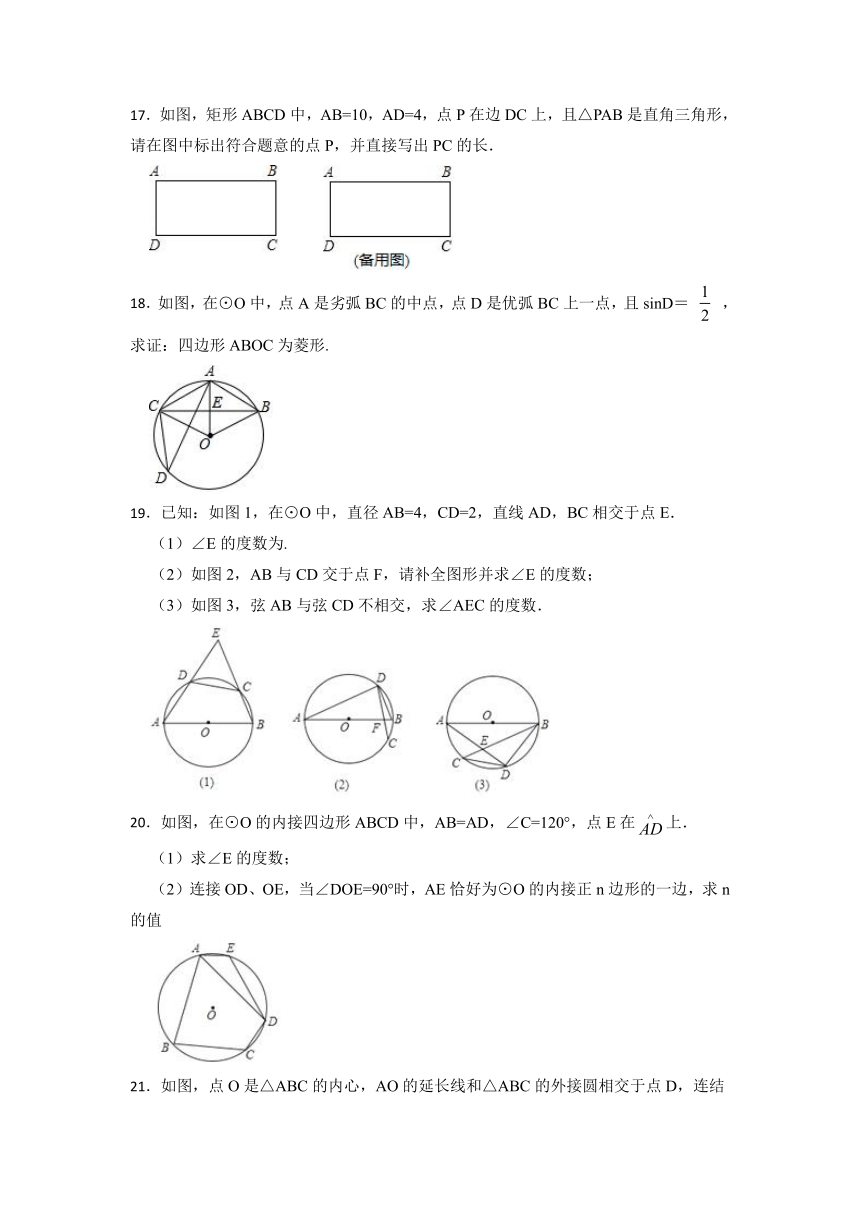
12.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE= ,则AE= .
13.如图,四边形ABCD内接于⊙O,若四边形AOCD是菱形,∠B的度数是 .
14.如图,点 、 、 、 、 在 上,且弧 为 ,则 .
15.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB= ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
三、解答题
16.如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC.
17.如图,矩形ABCD中,AB=10,AD=4,点P在边DC上,且△PAB是直角三角形,请在图中标出符合题意的点P,并直接写出PC的长.
18.如图,在⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且sinD= ,求证:四边形ABOC为菱形.
19.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为.
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
20.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值
21.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连结CD.
求证:OD=CD.
22.如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】A
11.【答案】60
12.【答案】
13.【答案】60°
14.【答案】155
15.【答案】
16.【答案】解:∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA="OB" M、N分别是OA、OB的中点
∴OM=ON,
在△MOC和△NOC中,
∴△MOC≌△NOC(SAS),
∴MC=NC.
17.【答案】解:如图,以AB的中点O为圆心,AB的一半5为半径作圆,交CD于点P,点P即为所求;
设PC=x,则PD=10﹣x,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∴∠DAP+∠APD=90°,
∵∠APB=90°,
∴∠APD+∠BPC=90°,
∴∠DAP=∠CPB,
∴△ADP∽△PCB,
∴ ,即 ,
解得:x=2或x=8,
即PC=2或PC=8
18.【答案】解:∵点A是劣弧BC的中点,
∴OA⊥BC,
∴∠AEB=90°,
∵∠D=∠ABE,
∴sin∠D=sin∠ABE= = ,
∴∠ABE=30°,
∴∠BAE=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=OB,
∵OA⊥BC,
∴
∴AC=AB,
∴AC=OC=OB=AB,
∴四边形ACOB是菱形.
19.【答案】解:(1)如图1,连结OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣300=600
∠E的度数为600;
(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连结OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
20.【答案】解:(1)连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴n==12.
21.【答案】证明:如图,连接OC,
∵点O是△ABC的内心,
∴∠CAD=∠BAD,∠OCA=∠OCB,
∵∠BAD=∠BCD,
∴∠COD=∠CAD+∠OCA=∠BAD+∠OCB,
∠DCO=∠BCD+∠OCB,
∴∠COD=∠DCO,
∴△DCO是等腰三角形,
∴OD=CD.
22.【答案】(1)证明:连接AB,∵OP⊥BC,∴BO=CO,∴AB=AC,又∵AC=AD,∴AB=AD,∴∠ABD=∠ADB,又∵∠ABD=∠ACF,∴∠ACF=∠ADB.(2)解:过点A作AM⊥CF交CF的延长线于M,过点A作AN⊥BF于N,连接AF,则AN=m,∴∠ANB=∠AMC=90°,在△ABN和△ACM中,∴Rt△ABN≌Rt△ACM(AAS)∴BN=CM,AN=AM,又∵∠ANF=∠AMF=90°,在Rt△AFN和Rt△AFM中,∴Rt△AFN≌Rt△AFM(HL),∴NF=MF,∴BF+CF=BN+NF+CM﹣MF,=BN+CM=2BN=n,∴BN=,∴在Rt△ABN中,AB2=BN2+AN2=m2+=m2+,在Rt△ACD中,CD2=AB2+AC2=2AB2=2m2+,∴CD=.(3)解:的值不发生变化,过点D作DH⊥AO于H,过点D作DQ⊥BC于Q,∵∠DAH+∠OAC=90°,∠DAH+∠ADH=90°,∴∠OAC=∠ADH,在△DHA和△AOC中,∴Rt△DHA≌Rt△AOC(AAS),∴DH=AO,AH=OC,又∵BO=OC,∴HO=AH+AO=OB+DH,而DH=OQ,HO=DQ,∴DQ=OB+OQ=BQ,∴∠DBQ=45°,又∵DH∥BC,∴∠HDE=45°,∴△DHE为等腰直角三角形,∴=,∴=.
一、单选题
1.如图,已知A,B,C在⊙O上, 的度数为300°,∠C的度数是( )
A.30° B.40° C.50° D.60°
2.如图,四边形ABCD为⊙O的内接四边形,若∠BCD=110°,则∠BAD为( )
A.140° B.110° C.90° D.70°
3.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=36°,那么∠BAD等于( ).
A.36° B.44° C.54° D.56°
4.如图,在平面直角坐标系中,点爿是双曲线y= 上的一点,以点爿为圆心,0A为半径画圆。交两坐标轴于点B,C.若OB=8,则OC的长为( )
A.2 B.4 C.2 D.6
5.有一直径为的圆,且圆上有、、、四点,其位置如图所示.若,,,,,则下列弧长关系何者正确?( )
A.,
B.,
C.,
D.,
6.如图,已知 是半圆O的直径,弦 相交于点P,若 ,则 的值( )
A. B. C. D.
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
8.如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的度数为( )
A.140° B.130° C.120° D.110°
9.如图,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为 ,AB=8,则BC的长是( )
A. B. C. D.
10.如图, 在 的正方形网格中, 经过格点A,B,C, 点P是 上任意一点, 连接AP, BP, 则 的值为( )
A. B. C. D.
二、填空题
11.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=30°,则∠CAD= 度.
12.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE= ,则AE= .
13.如图,四边形ABCD内接于⊙O,若四边形AOCD是菱形,∠B的度数是 .
14.如图,点 、 、 、 、 在 上,且弧 为 ,则 .
15.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB= ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
三、解答题
16.如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC.
17.如图,矩形ABCD中,AB=10,AD=4,点P在边DC上,且△PAB是直角三角形,请在图中标出符合题意的点P,并直接写出PC的长.
18.如图,在⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且sinD= ,求证:四边形ABOC为菱形.
19.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为.
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
20.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值
21.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连结CD.
求证:OD=CD.
22.如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】A
11.【答案】60
12.【答案】
13.【答案】60°
14.【答案】155
15.【答案】
16.【答案】解:∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA="OB" M、N分别是OA、OB的中点
∴OM=ON,
在△MOC和△NOC中,
∴△MOC≌△NOC(SAS),
∴MC=NC.
17.【答案】解:如图,以AB的中点O为圆心,AB的一半5为半径作圆,交CD于点P,点P即为所求;
设PC=x,则PD=10﹣x,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∴∠DAP+∠APD=90°,
∵∠APB=90°,
∴∠APD+∠BPC=90°,
∴∠DAP=∠CPB,
∴△ADP∽△PCB,
∴ ,即 ,
解得:x=2或x=8,
即PC=2或PC=8
18.【答案】解:∵点A是劣弧BC的中点,
∴OA⊥BC,
∴∠AEB=90°,
∵∠D=∠ABE,
∴sin∠D=sin∠ABE= = ,
∴∠ABE=30°,
∴∠BAE=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=OB,
∵OA⊥BC,
∴
∴AC=AB,
∴AC=OC=OB=AB,
∴四边形ACOB是菱形.
19.【答案】解:(1)如图1,连结OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣300=600
∠E的度数为600;
(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连结OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
20.【答案】解:(1)连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴n==12.
21.【答案】证明:如图,连接OC,
∵点O是△ABC的内心,
∴∠CAD=∠BAD,∠OCA=∠OCB,
∵∠BAD=∠BCD,
∴∠COD=∠CAD+∠OCA=∠BAD+∠OCB,
∠DCO=∠BCD+∠OCB,
∴∠COD=∠DCO,
∴△DCO是等腰三角形,
∴OD=CD.
22.【答案】(1)证明:连接AB,∵OP⊥BC,∴BO=CO,∴AB=AC,又∵AC=AD,∴AB=AD,∴∠ABD=∠ADB,又∵∠ABD=∠ACF,∴∠ACF=∠ADB.(2)解:过点A作AM⊥CF交CF的延长线于M,过点A作AN⊥BF于N,连接AF,则AN=m,∴∠ANB=∠AMC=90°,在△ABN和△ACM中,∴Rt△ABN≌Rt△ACM(AAS)∴BN=CM,AN=AM,又∵∠ANF=∠AMF=90°,在Rt△AFN和Rt△AFM中,∴Rt△AFN≌Rt△AFM(HL),∴NF=MF,∴BF+CF=BN+NF+CM﹣MF,=BN+CM=2BN=n,∴BN=,∴在Rt△ABN中,AB2=BN2+AN2=m2+=m2+,在Rt△ACD中,CD2=AB2+AC2=2AB2=2m2+,∴CD=.(3)解:的值不发生变化,过点D作DH⊥AO于H,过点D作DQ⊥BC于Q,∵∠DAH+∠OAC=90°,∠DAH+∠ADH=90°,∴∠OAC=∠ADH,在△DHA和△AOC中,∴Rt△DHA≌Rt△AOC(AAS),∴DH=AO,AH=OC,又∵BO=OC,∴HO=AH+AO=OB+DH,而DH=OQ,HO=DQ,∴DQ=OB+OQ=BQ,∴∠DBQ=45°,又∵DH∥BC,∴∠HDE=45°,∴△DHE为等腰直角三角形,∴=,∴=.
