2022-2023学年人教版七年级数学下册8.3实际问题与二元一次方程组 图表信息问题课件(共18张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册8.3实际问题与二元一次方程组 图表信息问题课件(共18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 08:22:22 | ||
图片预览




文档简介
(共18张PPT)
七年级数学下册(RJ) 教学课件
8.3
实际问题与二元一次方程组 ——图表信息问题
第八章 二元一次方程组
优翼
列二元一次方程组解应用题的一般步骤
创设情境
列二元一次方程组解应用题的一般步骤是什么?
1.审题:认真审题,分清题中的已知量、未知量,并明确它们之间的等量关系.
2.设元:用字母表示题目中的未知数.
3.列方程组:根据题中的等量关系列出方程组.
4.解方程组:解方程组,求出未知数的值.
5.检验并答:检验所求的解是否符合实际意义,然后作答.
新课导入
星期天,七年级1,2两个班的同学去公园玩碰碰车和划船,已知碰碰车的同学每人租用一辆车,划船的同学每4人合租一条船,两班各花了115元,活动人数如下表:
3.图表信息问题
班级 玩碰碰车的同学(个) 划船的同学(个)
1班 11 16
2班 8 20
每辆碰碰车租金多少元?每条船租金多少元?
解:每辆碰碰车租金x元,每条船租金y元.
根据题意得
11x+ y= 115
8x + y = 115
{
解得:
5
12
答:每辆碰碰车租金5元,每条船租金12元.
思路引导:由题可得两个等量关系
1班租11辆碰碰车+4条船=115
2班租8辆碰碰车+5条船=115
一、复习
对于已知条件较多的应用题我们爱采用表格的方式来分析问题
探究新知
探索分析,解决问题
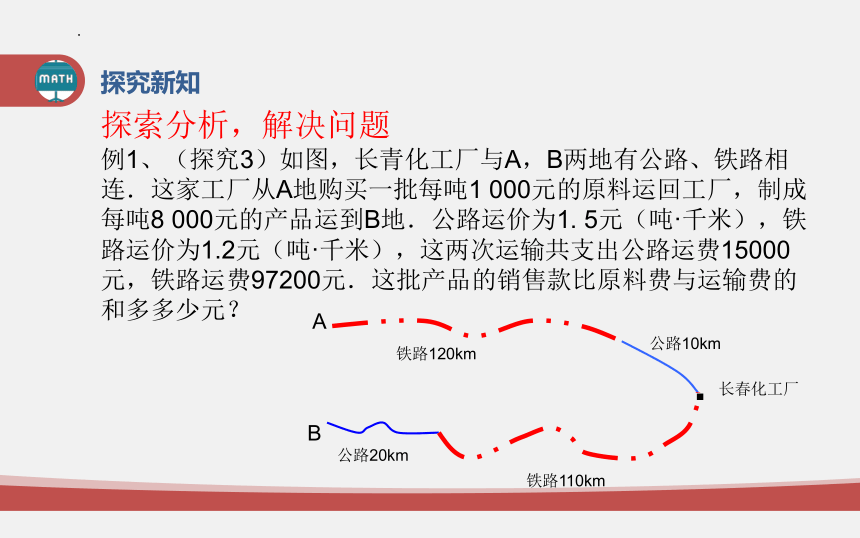
例1、(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
探究新知
设问1、原料的数量与产品的数量一样多吗?
(不一样)
设问2、那些量设为未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .
产品x吨重,原料y吨重
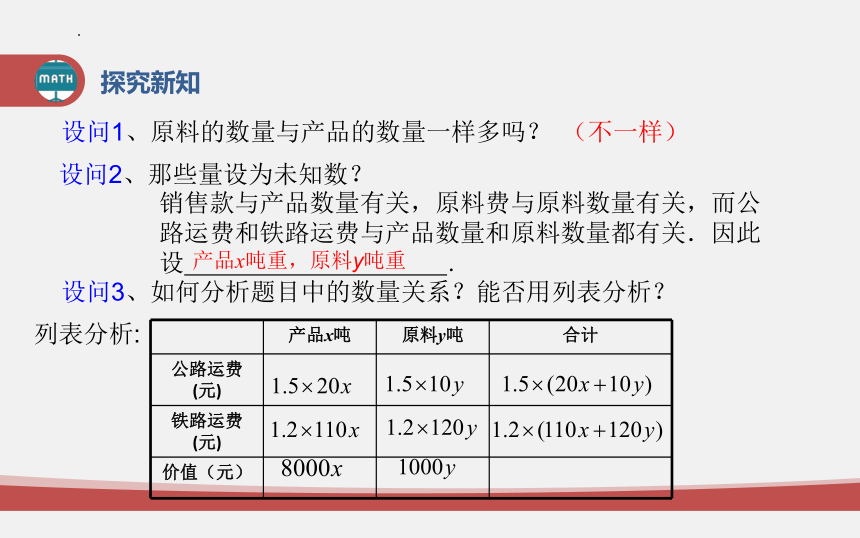
设问3、如何分析题目中的数量关系?能否用列表分析?
列表分析:
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
探究新知
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
解得,
答:这批产品的销售款比原料费与运输费的和多1887800元。
三、从表格中获取信息
例1.小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:(1)小丽买了自动铅笔、记号笔各几支?(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 单价(元) 数量(个) 金额(元)
签字笔 3 2 6
自动铅笔 1.5 ● ●
记号笔 4 ● ●
软皮笔记本 ● 2 9
圆规 3.5 1 ●
合计 8 28
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735(元).
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
答:货主应付运费735元.
北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
解:设从北京运往武汉x台,则运往重庆(10-x)台,设从上海运往武汉y台,则运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
答:从北京运往武汉4台,运往重庆6台,从上海运往武汉2台,运往重庆2台.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
四、从图形中获取信息
例2.小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是多少?
五、从对话中获取信息
例3.小明的妈妈在菜市场买回2斤萝卜和1斤排骨,准备做萝卜排骨汤,下面是他的爸爸和妈妈的一段对话:
小明根据爸爸、妈妈的对话,很快就知道了今天买的萝卜和排骨的单价,请你通过计算分别求出今天萝卜和排骨的单价.
练习
1、某校初一(8)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )A.
B.
C.
D.
练习
为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信:
自来水销售价格 污水处理价格
每户每月用水量 单价:元/吨 单价:元/吨
17吨及以下 a 0.80
超过17吨不超过30吨的部分 b 0.80
超过30吨的部分 6.00 0.80
已知小王家2021年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元,求a,b的值
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
利用二元一次方程组分析和解决实际问题的基本过程:
课堂小结
七年级数学下册(RJ) 教学课件
8.3
实际问题与二元一次方程组 ——图表信息问题
第八章 二元一次方程组
优翼
列二元一次方程组解应用题的一般步骤
创设情境
列二元一次方程组解应用题的一般步骤是什么?
1.审题:认真审题,分清题中的已知量、未知量,并明确它们之间的等量关系.
2.设元:用字母表示题目中的未知数.
3.列方程组:根据题中的等量关系列出方程组.
4.解方程组:解方程组,求出未知数的值.
5.检验并答:检验所求的解是否符合实际意义,然后作答.
新课导入
星期天,七年级1,2两个班的同学去公园玩碰碰车和划船,已知碰碰车的同学每人租用一辆车,划船的同学每4人合租一条船,两班各花了115元,活动人数如下表:
3.图表信息问题
班级 玩碰碰车的同学(个) 划船的同学(个)
1班 11 16
2班 8 20
每辆碰碰车租金多少元?每条船租金多少元?
解:每辆碰碰车租金x元,每条船租金y元.
根据题意得
11x+ y= 115
8x + y = 115
{
解得:
5
12
答:每辆碰碰车租金5元,每条船租金12元.
思路引导:由题可得两个等量关系
1班租11辆碰碰车+4条船=115
2班租8辆碰碰车+5条船=115
一、复习
对于已知条件较多的应用题我们爱采用表格的方式来分析问题
探究新知
探索分析,解决问题
例1、(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
探究新知
设问1、原料的数量与产品的数量一样多吗?
(不一样)
设问2、那些量设为未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .
产品x吨重,原料y吨重
设问3、如何分析题目中的数量关系?能否用列表分析?
列表分析:
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
探究新知
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
解得,
答:这批产品的销售款比原料费与运输费的和多1887800元。
三、从表格中获取信息
例1.小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:(1)小丽买了自动铅笔、记号笔各几支?(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 单价(元) 数量(个) 金额(元)
签字笔 3 2 6
自动铅笔 1.5 ● ●
记号笔 4 ● ●
软皮笔记本 ● 2 9
圆规 3.5 1 ●
合计 8 28
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735(元).
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
答:货主应付运费735元.
北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
解:设从北京运往武汉x台,则运往重庆(10-x)台,设从上海运往武汉y台,则运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
答:从北京运往武汉4台,运往重庆6台,从上海运往武汉2台,运往重庆2台.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
四、从图形中获取信息
例2.小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是多少?
五、从对话中获取信息
例3.小明的妈妈在菜市场买回2斤萝卜和1斤排骨,准备做萝卜排骨汤,下面是他的爸爸和妈妈的一段对话:
小明根据爸爸、妈妈的对话,很快就知道了今天买的萝卜和排骨的单价,请你通过计算分别求出今天萝卜和排骨的单价.
练习
1、某校初一(8)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )A.
B.
C.
D.
练习
为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信:
自来水销售价格 污水处理价格
每户每月用水量 单价:元/吨 单价:元/吨
17吨及以下 a 0.80
超过17吨不超过30吨的部分 b 0.80
超过30吨的部分 6.00 0.80
已知小王家2021年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元,求a,b的值
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
利用二元一次方程组分析和解决实际问题的基本过程:
课堂小结
