2022-2023学年北师大版七年级数学下册5.3 简单的轴对称图形 同步练习(含解析)
文档属性
| 名称 | 2022-2023学年北师大版七年级数学下册5.3 简单的轴对称图形 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 554.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 00:00:00 | ||
图片预览



文档简介
北师大版七下 5.3 简单的轴对称图形
一、选择题(共9小题)
1. 等腰三角形是轴对称图形,它的对称轴是
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线 D. 底边的垂直平分线
2. 到三角形三边距离相等的点是
A. 三条边中线的交点 B. 三条边的高的交点
C. 三个角的角平分线的交点 D. 三条边的垂直平分线的交点
3. 如图,在 中,, ,以 为圆心,任意长为半径画弧,分别交 、 于点 和 ,再分别以 、 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点 ,下列结论:
① 是 的平分线;② ;③ ;④ .
其中正确的结论共有
A. 个 B. 个 C. 个 D. 个
4. 已知 (),用尺规在线段 上确定一点 ,使得 ,则符合要求的作图痕迹是
A. B.
C. D.
5. 如图,在 中,求作一点 ,使点 到 两边的距离相等,且 .下列确定点 的方法正确的是
A. 为 , 平分线的交点
B. 为 的平分线与 的垂直平分线的交点
C. 为 , 两边上的高的交点
D. 为 , 两边的垂直平分线的交点
6. 如图,在 中, 的垂直平分线分别交 , 于 , 两点,, 的周长为 ,则 的周长为
A. B. C. D.
7. 如图,点 是 的 边上一点,点 在 上, 是 的中点,且 ,给出下列结论:① ;② ;③ ;④ .其中正确的结论有
A. 个 B. 个 C. 个 D. 个
8. 如图所示,下面是利用尺规作 的角平分线 的作法,在用尺规作角平分线的过程中,用到的三角形全等的判定方法是
作法:
①以点 为圆心,适当长为半径画弧,分别交 , 于点 ,;
②分别以点 , 为圆心,大于 的长为半径画弧,两弧在 内交于一点 ;
③画射线 ,射线 就是 的角平分线.
A. B. C. D.
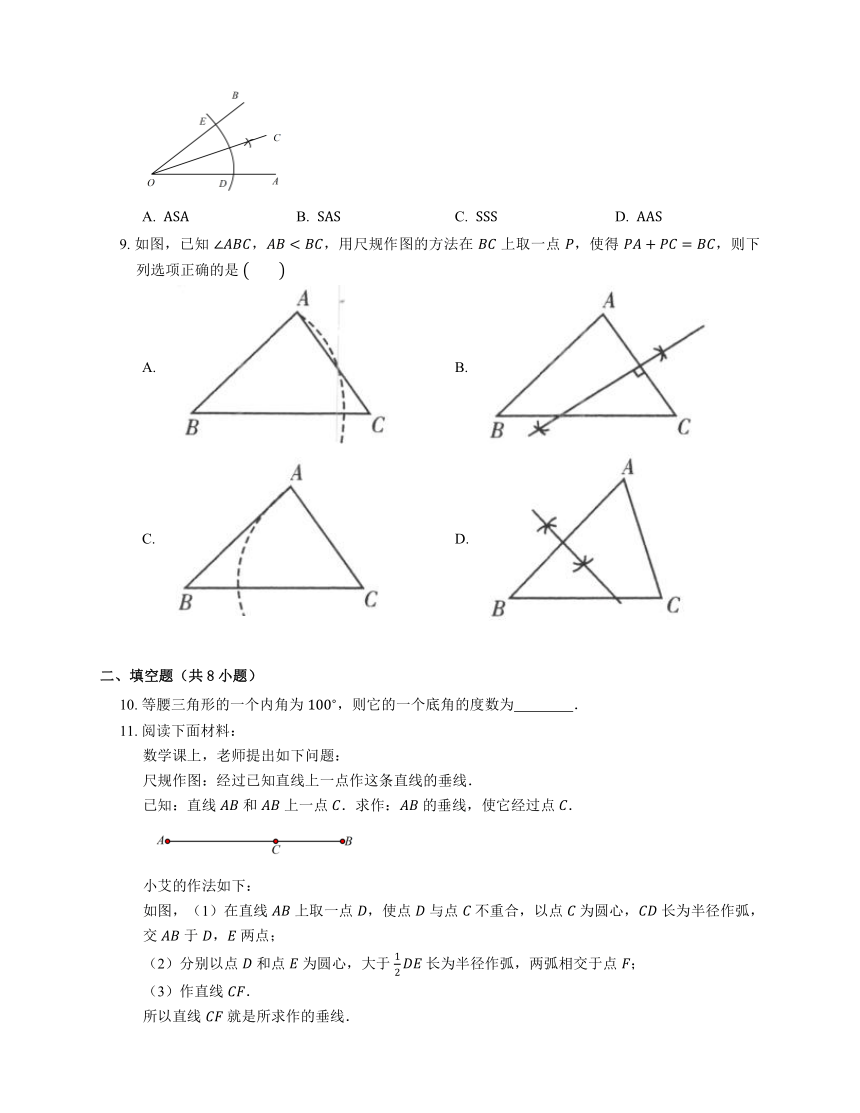
9. 如图,已知 ,,用尺规作图的方法在 上取一点 ,使得 ,则下列选项正确的是
A. B.
C. D.
二、填空题(共8小题)
10. 等腰三角形的一个内角为 ,则它的一个底角的度数为 .
11. 阅读下面材料:
数学课上,老师提出如下问题:
尺规作图:经过已知直线上一点作这条直线的垂线.
已知:直线 和 上一点 .求作: 的垂线,使它经过点 .
小艾的作法如下:
如图,(1)在直线 上取一点 ,使点 与点 不重合,以点 为圆心, 长为半径作弧,交 于 , 两点;
(2)分别以点 和点 为圆心,大于 长为半径作弧,两弧相交于点 ;
(3)作直线 .
所以直线 就是所求作的垂线.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是 .
12. 如图,,以点 为圆心,以适当长为半径作弧分别交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 以 为端点作射线 ,在射线 上取点 ,连接 ,.若测得 ,则 .
13. 如图, 中,, 平分 ,,,则 的面积是 .
14. 如图,在 中, 是 的垂直平分线,, 的周长为 ,则 的周长 .
15. 如图,已知 ,则 .
16. 如图,在 中,, 的垂直平分线分别交 , 于点 ,.若 的周长等于 ,则 的长为 .
17. 如图,在 中,,,, 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是 .
三、解答题(共7小题)
18. 在以下图形中找出轴对称图形,并画出一条对称轴:
19. 如图,在一条河的同岸有两个村庄 和 ,两村要在河上合修一座便民桥,桥修在什么地方可以使桥到两村的距离之和最短
20. 一艘游船早上 从港口出发,沿北偏东 方向航行,上午 正好抵达 岛,游客们在 岛游玩后,下午乘坐游船再沿东南方向继续航行,到达 岛, 岛恰好在港口的正东方向.若游船的速度为每小时 千米,请试一试按照 的比例画出游船行进路线.
21. 如图,在 中,,, 是 的边 上的中线, 的延长线交 于点 ,那么 吗 请说明理由.
22. 三条公路 ,, 两两相交于 ,, 三点,现计划修建一个商品超市,要求这个超市到三条公路的距离相等,问可供选择的地方有多少处 请画出图形并在图中找出来.
23. 如图,点 和点 在 内部.
(1)请你作出点 ,使点 到点 和点 的距离相等,且到 两边的距离也相等(保留作图痕迹,不写作法);
(2)请说明作图理由.
24. 若两个角的两边分别垂直,其中一个角比另一个角的 倍少 ,求这两个角的度数.
答案
1. D
2. C
3. A
4. D
【解析】由 ,可得 ,则点 在线段 的垂直平分线上.
5. B
6. B
7. B 【解析】① 是 的中点,,
;故①正确;
② 在 上,不一定是 的中点,,
无法证明 ,故②错误;
③无法证明 ,故③错误;
④ 是 的中点,
,
,
,故④正确.
故其中正确的结论有①④.
8. C
9. D
10.
【解析】①当这个角是顶角时,底角 ;
②当这个角是底角时,另一个底角为 ,因为 ,不符合三角形内角和定理,所以舍去.
11. 等腰三角形“三线合一”,两点确定一条直线.
12.
【解析】由作法得 , 平分 ,
则 ,
在 和 中,
,
,
.
13.
【解析】由题意可知 点到 的距离等于 .
.
14.
【解析】 是 的垂直平分线,,
,,
,
的周长为 ,
即 ,
即 ,
的周长 .
故答案为 .
15.
【解析】,
,
.
,,
.
16.
【解析】 是 的垂直平分线,
,
, 的周长等于 ,
,
,
.
17.
【解析】如图,过点 作 交 于点 ,交 于点 ,过点 作 于点 .
是 的平分线.
,这时 有最小值,即 的长度,
,,,
.
,
.
18. ()()()是轴对称图形.
19. 如图作点 关于河岸的对称点 ,连接 交河岸于点 ,点 就是桥的位置.
理由:两点之间线段最短.
20.
折线 就是游船行进的路线.
21. 由 , 是 边 上的中线,可得 平分 ;再由 ,可得 .
22. 先将实际问题转化为数学模型,要求超市到三条公路的距离相等,先观察 的内部,实际上就是在 内找一个点,使它到 的三边的距离相等,这应该是 的三条(或两条)角平分线的交点,但除此以外,还应考虑是否还有其他的点也符合要求,因为三条公路都是用直线来表示的,且三角形互为同旁内角的两个外角的平分线的交点到三角形三边所在直线的距离相等,所以在 的外部也存在满足题意的点.
如图,()作出 的两个内角的平分线,取其交点为 ;
()作出 所有外角( 个外角)的平分线,取其交点分别为 ,,,故满足条件的修建点有 处,即 ,,, 处.
23. (1) 如图所示.
(2) 作图的理由:点 在 的平分线上,又在线段 的垂直平分线上, 的平分线和线段 的垂直平分线的交点即为所求.
24. 设另一个角的度数为 ,则这个角的度数是 .
因为两个角的两边分别垂直,
所以
解得
所以 或 .
故这两个角的度数分别是 , 或 ,.
一、选择题(共9小题)
1. 等腰三角形是轴对称图形,它的对称轴是
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线 D. 底边的垂直平分线
2. 到三角形三边距离相等的点是
A. 三条边中线的交点 B. 三条边的高的交点
C. 三个角的角平分线的交点 D. 三条边的垂直平分线的交点
3. 如图,在 中,, ,以 为圆心,任意长为半径画弧,分别交 、 于点 和 ,再分别以 、 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点 ,下列结论:
① 是 的平分线;② ;③ ;④ .
其中正确的结论共有
A. 个 B. 个 C. 个 D. 个
4. 已知 (),用尺规在线段 上确定一点 ,使得 ,则符合要求的作图痕迹是
A. B.
C. D.
5. 如图,在 中,求作一点 ,使点 到 两边的距离相等,且 .下列确定点 的方法正确的是
A. 为 , 平分线的交点
B. 为 的平分线与 的垂直平分线的交点
C. 为 , 两边上的高的交点
D. 为 , 两边的垂直平分线的交点
6. 如图,在 中, 的垂直平分线分别交 , 于 , 两点,, 的周长为 ,则 的周长为
A. B. C. D.
7. 如图,点 是 的 边上一点,点 在 上, 是 的中点,且 ,给出下列结论:① ;② ;③ ;④ .其中正确的结论有
A. 个 B. 个 C. 个 D. 个
8. 如图所示,下面是利用尺规作 的角平分线 的作法,在用尺规作角平分线的过程中,用到的三角形全等的判定方法是
作法:
①以点 为圆心,适当长为半径画弧,分别交 , 于点 ,;
②分别以点 , 为圆心,大于 的长为半径画弧,两弧在 内交于一点 ;
③画射线 ,射线 就是 的角平分线.
A. B. C. D.
9. 如图,已知 ,,用尺规作图的方法在 上取一点 ,使得 ,则下列选项正确的是
A. B.
C. D.
二、填空题(共8小题)
10. 等腰三角形的一个内角为 ,则它的一个底角的度数为 .
11. 阅读下面材料:
数学课上,老师提出如下问题:
尺规作图:经过已知直线上一点作这条直线的垂线.
已知:直线 和 上一点 .求作: 的垂线,使它经过点 .
小艾的作法如下:
如图,(1)在直线 上取一点 ,使点 与点 不重合,以点 为圆心, 长为半径作弧,交 于 , 两点;
(2)分别以点 和点 为圆心,大于 长为半径作弧,两弧相交于点 ;
(3)作直线 .
所以直线 就是所求作的垂线.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是 .
12. 如图,,以点 为圆心,以适当长为半径作弧分别交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 以 为端点作射线 ,在射线 上取点 ,连接 ,.若测得 ,则 .
13. 如图, 中,, 平分 ,,,则 的面积是 .
14. 如图,在 中, 是 的垂直平分线,, 的周长为 ,则 的周长 .
15. 如图,已知 ,则 .
16. 如图,在 中,, 的垂直平分线分别交 , 于点 ,.若 的周长等于 ,则 的长为 .
17. 如图,在 中,,,, 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是 .
三、解答题(共7小题)
18. 在以下图形中找出轴对称图形,并画出一条对称轴:
19. 如图,在一条河的同岸有两个村庄 和 ,两村要在河上合修一座便民桥,桥修在什么地方可以使桥到两村的距离之和最短
20. 一艘游船早上 从港口出发,沿北偏东 方向航行,上午 正好抵达 岛,游客们在 岛游玩后,下午乘坐游船再沿东南方向继续航行,到达 岛, 岛恰好在港口的正东方向.若游船的速度为每小时 千米,请试一试按照 的比例画出游船行进路线.
21. 如图,在 中,,, 是 的边 上的中线, 的延长线交 于点 ,那么 吗 请说明理由.
22. 三条公路 ,, 两两相交于 ,, 三点,现计划修建一个商品超市,要求这个超市到三条公路的距离相等,问可供选择的地方有多少处 请画出图形并在图中找出来.
23. 如图,点 和点 在 内部.
(1)请你作出点 ,使点 到点 和点 的距离相等,且到 两边的距离也相等(保留作图痕迹,不写作法);
(2)请说明作图理由.
24. 若两个角的两边分别垂直,其中一个角比另一个角的 倍少 ,求这两个角的度数.
答案
1. D
2. C
3. A
4. D
【解析】由 ,可得 ,则点 在线段 的垂直平分线上.
5. B
6. B
7. B 【解析】① 是 的中点,,
;故①正确;
② 在 上,不一定是 的中点,,
无法证明 ,故②错误;
③无法证明 ,故③错误;
④ 是 的中点,
,
,
,故④正确.
故其中正确的结论有①④.
8. C
9. D
10.
【解析】①当这个角是顶角时,底角 ;
②当这个角是底角时,另一个底角为 ,因为 ,不符合三角形内角和定理,所以舍去.
11. 等腰三角形“三线合一”,两点确定一条直线.
12.
【解析】由作法得 , 平分 ,
则 ,
在 和 中,
,
,
.
13.
【解析】由题意可知 点到 的距离等于 .
.
14.
【解析】 是 的垂直平分线,,
,,
,
的周长为 ,
即 ,
即 ,
的周长 .
故答案为 .
15.
【解析】,
,
.
,,
.
16.
【解析】 是 的垂直平分线,
,
, 的周长等于 ,
,
,
.
17.
【解析】如图,过点 作 交 于点 ,交 于点 ,过点 作 于点 .
是 的平分线.
,这时 有最小值,即 的长度,
,,,
.
,
.
18. ()()()是轴对称图形.
19. 如图作点 关于河岸的对称点 ,连接 交河岸于点 ,点 就是桥的位置.
理由:两点之间线段最短.
20.
折线 就是游船行进的路线.
21. 由 , 是 边 上的中线,可得 平分 ;再由 ,可得 .
22. 先将实际问题转化为数学模型,要求超市到三条公路的距离相等,先观察 的内部,实际上就是在 内找一个点,使它到 的三边的距离相等,这应该是 的三条(或两条)角平分线的交点,但除此以外,还应考虑是否还有其他的点也符合要求,因为三条公路都是用直线来表示的,且三角形互为同旁内角的两个外角的平分线的交点到三角形三边所在直线的距离相等,所以在 的外部也存在满足题意的点.
如图,()作出 的两个内角的平分线,取其交点为 ;
()作出 所有外角( 个外角)的平分线,取其交点分别为 ,,,故满足条件的修建点有 处,即 ,,, 处.
23. (1) 如图所示.
(2) 作图的理由:点 在 的平分线上,又在线段 的垂直平分线上, 的平分线和线段 的垂直平分线的交点即为所求.
24. 设另一个角的度数为 ,则这个角的度数是 .
因为两个角的两边分别垂直,
所以
解得
所以 或 .
故这两个角的度数分别是 , 或 ,.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
