圆柱的表面积(课件) 六年级下册数学北师大版(共26张PPT)
文档属性
| 名称 | 圆柱的表面积(课件) 六年级下册数学北师大版(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-26 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第一单元
第2课时
圆柱的表面积
北师大版六年级数学下册
复习导入
1、我们知道长方体6个面的总面积,叫做它的表面积。表面积的定义是
什么?
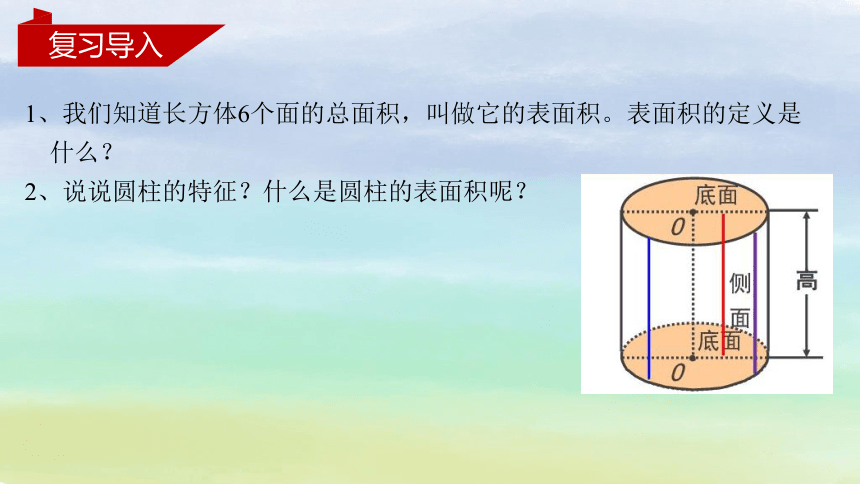
2、说说圆柱的特征?什么是圆柱的表面积呢?
1、通过研究圆柱的展开图,你能说出圆柱的侧面积及表面积的计算方法吗?
2、你能总结出生活中圆柱有几种类型,以及它们表面积的计算方法吗?
学习目标
1、圆柱表面积计算公式推导。
2、圆柱有几种类型,以及它们表面积的计算方法。
关键问题建议
1、习读内容:数学课本第5页。
2、习读问题:(1)圆柱的侧面积及表面积指的分别是哪些面的面积?
(2)圆柱侧面展开是什么形状?
(3)圆柱的侧面积和表面积的计算方法是什么?
3、习读要求:认真阅读习读材料,红笔批注关键信息、黑笔记录问题。
习读
精讲(一)--圆柱侧面积公式推导
1、圆柱的侧面展开是什么形状?
沿着斜线剪开,可以得到一个平行四边形。
沿着高剪开,可以得到一个长方形。
沿着高剪开,还可能得到一个正方形。
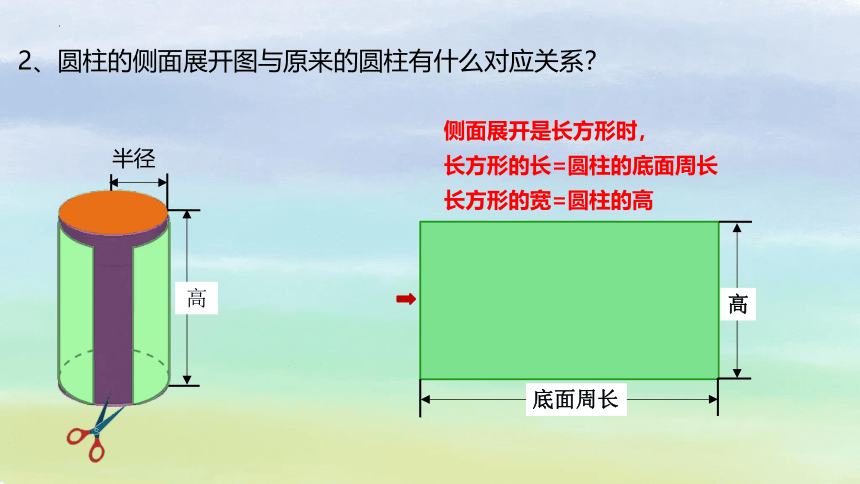
2、圆柱的侧面展开图与原来的圆柱有什么对应关系?
半径
高
底面周长
高
侧面展开是长方形时,
长方形的长=圆柱的底面周长
长方形的宽=圆柱的高
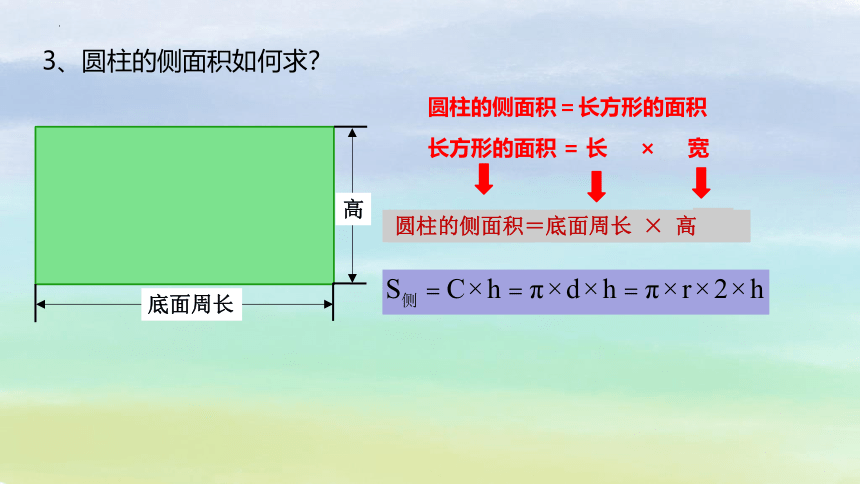
3、圆柱的侧面积如何求?
底面周长
高
圆柱的侧面积=长方形的面积
长方形的面积 = 长 × 宽
底面周长
高
圆柱的侧面积
圆柱的侧面积=底面周长 × 高
精讲(二)--表面积公式推导
1、圆柱的表面积由哪几个面组成?
3个面,一个侧面,2个底面。
2、圆柱的表面积如何计算?
S表=S侧+2S底
圆柱的表面积=侧面积+底面积×2
= πdh+πr2×2
=Ch+πr2×2
=2πrh+πr2×2
你能计算出“至少需要多大面积的纸板”吗?
10cm
30cm
侧面积:
底面积:
表面积:
答:至少需要2512平方厘米的纸板。
2×3.14×10×30=1884(cm2)
3.14×10×10=314(cm2)
314×2+1884=2512(cm2)
习读精讲(三)--表面积计算
1、连一连,并在括号中填出相应的数。
( )
( )
( )
( )
4cm
7×3.14=21.98cm
8cm
3×3.14=9.42cm
习读检测
2.求圆柱的表面积。
表面积:
4π×2+24π=32π=100.48(cm2)
侧面积:
底面积:
4×3.14×6=24π(cm2)
3.14×(4÷2)2=4π(cm2)
表面积:
9π×2+60π
=78π
=244.92(dm2)
侧面积:
底面积:
2×3×3.14×10=60π(dm2)
3.14×3×3=9π(dm2)
3. 如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10cm
18.84cm
cm
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×3×3=28.26(cm2)
表面积:
28.26×2+188.4=244.92(cm2)
答:这个薯片盒的侧面积是188.4cm2,表面积是244.92cm2。
4. 如图,做一个无盖 的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
表面积:
4π+20 π
侧面积:
底面积:
4×3.14×5=20π(dm2)
3.14×(4÷2)2=4π(dm2)
=24π
答:至少需要75.36平方分米的铁皮。
1个侧面+1个底面
=75.36(dm2)
5. 制作一个底面直径20cm,长50cm的圆柱形通风管,至少要用多少平方厘米铁皮?
3.14×20×50=3140(cm2)
答:至少需要3140平方厘米的铁皮。
1个侧面
习研
习研内容:
1、能解决习读检测中的个人问题。
2、总结生活中的不同圆柱物体表面积计算的方法。
习研要求:
1、全员参与,讨论有序;
2、声音小组内听到即可;
3、有记录和总结。
习说
1、你的疑惑是什么?
2、解决计算生活中的圆柱物体的表面积注意事项有哪些?
3、你的收获是什么?
2.普通圆柱:包括1个侧面+2个底面
底面积=π×r×r
侧面积=π×r×2×h=C×h
表面积=底面积×2+侧面积
3. 无盖水桶:包括1个侧面+1个底面
底面积=π×r×r
侧面积=π×r×2×h=C×h
表面积=底面积+侧面积
4. 通风管:包括1个侧面
侧面积=π×r×2×h=C×h
表面积=侧面积
习说小结
1.圆柱的侧面展开是一个长方形时,长方形的长=圆柱底面圆的周长
宽=圆柱的高
1、把一个底面半径为4dm、高为5dm的圆柱的侧面沿高剪开后,可以得到一个( ),它的长为( )dm,宽为( )dm,这个圆柱的侧面积为( )dm2。
2、一个圆柱的侧面积是62.8cm2,高是5cm,底面周长是( )cm,底面半径是( )cm,底面积是( )cm2,表面积是( )cm2。
习练
长方形
25.12
5
125.6
12.56
2
12.56
87.92
3、一台压路机的滚筒宽1.2米,直径为8分米。如果它滚动1周,压路的面积是多少平方米?
3.14×0.8×1.2=3.0144(m2)
8分米 = 0.8米
1、一个无盖的圆柱形铁皮水桶,它的高为6.28dm,将它的侧面沿高展开后正好是一个正方形,做这个水桶至少需要多少平方分米的铁皮?(得数保留整数)。
动态模块
底面周长 = 高
底面半径:
6.28÷3.14÷2=1(dm)
底面:
3.14×1×1=3.14(dm2)
侧面:
6.28×6.28=39.4384(dm2)
合计:
3.14+39.4384=42.5784(dm2)
2、一个圆柱,如果高减少2cm,它的表面积就减少18.84cm2,这个圆柱的底面积是多少平方厘米
减少的为高是2cm的圆柱的侧面积
底面周长:
18.84÷2=9.42(cm)
底面半径:
9.42÷3.14÷2=1.5(cm)
底面积:
3.14×1.5×1.5=7.065(cm2)
3、一根圆柱形钢材长2m,底面直径为10cm,把它截成若干段后,每一段的形状都是圆柱,其表面积增加了471cm2 ,圆柱形钢材被截成了几段?
6÷2+1=4(段)
底面积:
10÷2=5(cm)
3.14×5×5=78.5(cm2)
471÷78.5=6(个)
1、订正错题,完善笔记;
2、完成《表面积习题》。
3、建议完成时间:30分钟,检查5分钟。
作业
先整理课堂笔记,梳理知识点,再做作业!
第一单元
第2课时
圆柱的表面积
北师大版六年级数学下册
复习导入
1、我们知道长方体6个面的总面积,叫做它的表面积。表面积的定义是
什么?
2、说说圆柱的特征?什么是圆柱的表面积呢?
1、通过研究圆柱的展开图,你能说出圆柱的侧面积及表面积的计算方法吗?
2、你能总结出生活中圆柱有几种类型,以及它们表面积的计算方法吗?
学习目标
1、圆柱表面积计算公式推导。
2、圆柱有几种类型,以及它们表面积的计算方法。
关键问题建议
1、习读内容:数学课本第5页。
2、习读问题:(1)圆柱的侧面积及表面积指的分别是哪些面的面积?
(2)圆柱侧面展开是什么形状?
(3)圆柱的侧面积和表面积的计算方法是什么?
3、习读要求:认真阅读习读材料,红笔批注关键信息、黑笔记录问题。
习读
精讲(一)--圆柱侧面积公式推导
1、圆柱的侧面展开是什么形状?
沿着斜线剪开,可以得到一个平行四边形。
沿着高剪开,可以得到一个长方形。
沿着高剪开,还可能得到一个正方形。
2、圆柱的侧面展开图与原来的圆柱有什么对应关系?
半径
高
底面周长
高
侧面展开是长方形时,
长方形的长=圆柱的底面周长
长方形的宽=圆柱的高
3、圆柱的侧面积如何求?
底面周长
高
圆柱的侧面积=长方形的面积
长方形的面积 = 长 × 宽
底面周长
高
圆柱的侧面积
圆柱的侧面积=底面周长 × 高
精讲(二)--表面积公式推导
1、圆柱的表面积由哪几个面组成?
3个面,一个侧面,2个底面。
2、圆柱的表面积如何计算?
S表=S侧+2S底
圆柱的表面积=侧面积+底面积×2
= πdh+πr2×2
=Ch+πr2×2
=2πrh+πr2×2
你能计算出“至少需要多大面积的纸板”吗?
10cm
30cm
侧面积:
底面积:
表面积:
答:至少需要2512平方厘米的纸板。
2×3.14×10×30=1884(cm2)
3.14×10×10=314(cm2)
314×2+1884=2512(cm2)
习读精讲(三)--表面积计算
1、连一连,并在括号中填出相应的数。
( )
( )
( )
( )
4cm
7×3.14=21.98cm
8cm
3×3.14=9.42cm
习读检测
2.求圆柱的表面积。
表面积:
4π×2+24π=32π=100.48(cm2)
侧面积:
底面积:
4×3.14×6=24π(cm2)
3.14×(4÷2)2=4π(cm2)
表面积:
9π×2+60π
=78π
=244.92(dm2)
侧面积:
底面积:
2×3×3.14×10=60π(dm2)
3.14×3×3=9π(dm2)
3. 如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10cm
18.84cm
cm
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×3×3=28.26(cm2)
表面积:
28.26×2+188.4=244.92(cm2)
答:这个薯片盒的侧面积是188.4cm2,表面积是244.92cm2。
4. 如图,做一个无盖 的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
表面积:
4π+20 π
侧面积:
底面积:
4×3.14×5=20π(dm2)
3.14×(4÷2)2=4π(dm2)
=24π
答:至少需要75.36平方分米的铁皮。
1个侧面+1个底面
=75.36(dm2)
5. 制作一个底面直径20cm,长50cm的圆柱形通风管,至少要用多少平方厘米铁皮?
3.14×20×50=3140(cm2)
答:至少需要3140平方厘米的铁皮。
1个侧面
习研
习研内容:
1、能解决习读检测中的个人问题。
2、总结生活中的不同圆柱物体表面积计算的方法。
习研要求:
1、全员参与,讨论有序;
2、声音小组内听到即可;
3、有记录和总结。
习说
1、你的疑惑是什么?
2、解决计算生活中的圆柱物体的表面积注意事项有哪些?
3、你的收获是什么?
2.普通圆柱:包括1个侧面+2个底面
底面积=π×r×r
侧面积=π×r×2×h=C×h
表面积=底面积×2+侧面积
3. 无盖水桶:包括1个侧面+1个底面
底面积=π×r×r
侧面积=π×r×2×h=C×h
表面积=底面积+侧面积
4. 通风管:包括1个侧面
侧面积=π×r×2×h=C×h
表面积=侧面积
习说小结
1.圆柱的侧面展开是一个长方形时,长方形的长=圆柱底面圆的周长
宽=圆柱的高
1、把一个底面半径为4dm、高为5dm的圆柱的侧面沿高剪开后,可以得到一个( ),它的长为( )dm,宽为( )dm,这个圆柱的侧面积为( )dm2。
2、一个圆柱的侧面积是62.8cm2,高是5cm,底面周长是( )cm,底面半径是( )cm,底面积是( )cm2,表面积是( )cm2。
习练
长方形
25.12
5
125.6
12.56
2
12.56
87.92
3、一台压路机的滚筒宽1.2米,直径为8分米。如果它滚动1周,压路的面积是多少平方米?
3.14×0.8×1.2=3.0144(m2)
8分米 = 0.8米
1、一个无盖的圆柱形铁皮水桶,它的高为6.28dm,将它的侧面沿高展开后正好是一个正方形,做这个水桶至少需要多少平方分米的铁皮?(得数保留整数)。
动态模块
底面周长 = 高
底面半径:
6.28÷3.14÷2=1(dm)
底面:
3.14×1×1=3.14(dm2)
侧面:
6.28×6.28=39.4384(dm2)
合计:
3.14+39.4384=42.5784(dm2)
2、一个圆柱,如果高减少2cm,它的表面积就减少18.84cm2,这个圆柱的底面积是多少平方厘米
减少的为高是2cm的圆柱的侧面积
底面周长:
18.84÷2=9.42(cm)
底面半径:
9.42÷3.14÷2=1.5(cm)
底面积:
3.14×1.5×1.5=7.065(cm2)
3、一根圆柱形钢材长2m,底面直径为10cm,把它截成若干段后,每一段的形状都是圆柱,其表面积增加了471cm2 ,圆柱形钢材被截成了几段?
6÷2+1=4(段)
底面积:
10÷2=5(cm)
3.14×5×5=78.5(cm2)
471÷78.5=6(个)
1、订正错题,完善笔记;
2、完成《表面积习题》。
3、建议完成时间:30分钟,检查5分钟。
作业
先整理课堂笔记,梳理知识点,再做作业!
