2022-2023学年沪科版数学七年级下册7.4 综合与实践 排队问题 同步训练(含解析)
文档属性
| 名称 | 2022-2023学年沪科版数学七年级下册7.4 综合与实践 排队问题 同步训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 506.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 14:48:26 | ||
图片预览




文档简介
7.4 综合与实践 排队问题 同步训练(含分析、答案)
一、单选题
1.、、、四人去玩跷跷板,由下面示意图,判断这四人轻重正确的是( )
A. B. C. D.
2.某电梯标明“载客不超过13人”,设载客人数为x(x为自然数),则“载客不超过13人”用不等式表示为 ( )
A.0<x<13 B.1≤x≤13 C.0≤x≤13 D.x≥13
3.某电脑用户使用不超过530元资金购买单价为70元的单片软件和80元的盒装磁带,根据需要,软件至少买3片,磁盘至少买2盒,则不相同的购买方式共有( )
A.4 种 B.5 种 C.6 种 D.7 种
4.对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次就停止了,那么x的取值范围是( )
A.8<x≤22 B.8≤x<22 C.8<x≤64 D.22<x≤64
5.已知关于x的不等式组的所有整数解的和为,满足条件的所有整数m的和是( )
A.13 B.-15 C.-2 D.0
6.将一箱苹果分给若干个学生,每个学生都分到苹果.若每个学生分5个苹果,则还剩12个苹果;若每位学生分8个苹果,则有一个学生所分苹果不足8个.若学生的人数为,则列式正确的是( )
A. B.
C. D.
7.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,①输入整数11,输出结果为27;②若输入整数x后程序操作仅进行了两次就停止,则x的最大值是8;③若操作停止时输出结果为21,则输入的整数x是9;④输入整数x后,该操作永不停止,则,以上结论正确有( )
A.①② B.①②③ C.①③④ D.①②④
8.如图,是一个运算流程,若需要经过两次运算,才能运算出,则的取值范围是( )
A. B. C. D.
9.五月初五端午节这天,妈妈让小明去超市买豆沙馅和蛋黄鲜肉馅的粽子.豆沙馅的每个卖2元,蛋黄鲜肉馅的每个卖3元,两种的粽子至少各买一个,买粽子的总钱数不能超过15元.则不同的购买方案的个数为( )
A.11 B.12 C.13 D.14
10.某登山队在野外露营,每个帐篷住5人,有3人没地方住,若每个帐篷住7人,则空出一个帐篷,还有一个帐篷不空.那么这个登山队不可能有( )人.
A.23 B.28 C.33 D.38
二、填空题
11.有若干糖果要分给小朋友,若每人分3个,则余8个;每人分5个,则最后一个小朋友能分到糖果但个数不足3个,则共有________个小朋友.
12.某生物兴趣小组要在恒温箱中培养A,B两种菌种,A菌种生长的温度在20~28℃之间(不包括20℃、28℃),B菌种生长的温度在 25~33℃之间(不包括25℃、33℃),若设恒温箱的温度为t℃,则t所满足的不等式为_______.
13.七年级学生张明的母亲给他150元钱,作为他一周在校五天的生活费,假定张明平均每天所用的生活费为a元,且到周末略有剩余,则a的取值范围是_________.
14.海口市某中学举行党史知识竞赛.竞赛共有20道题,规定答对一道题得10分,答错或不答扣5分,本次竞赛中晨晨同学要超过90分才能晋级,则她至少答对__________道题.
15.把一筐梨分给几个学生,若每人4个,则剩下3个;若每人6个,则最后一个同学最多分得3个,求学生人数和梨的个数.设有a个学生,则可列不等式组为____.
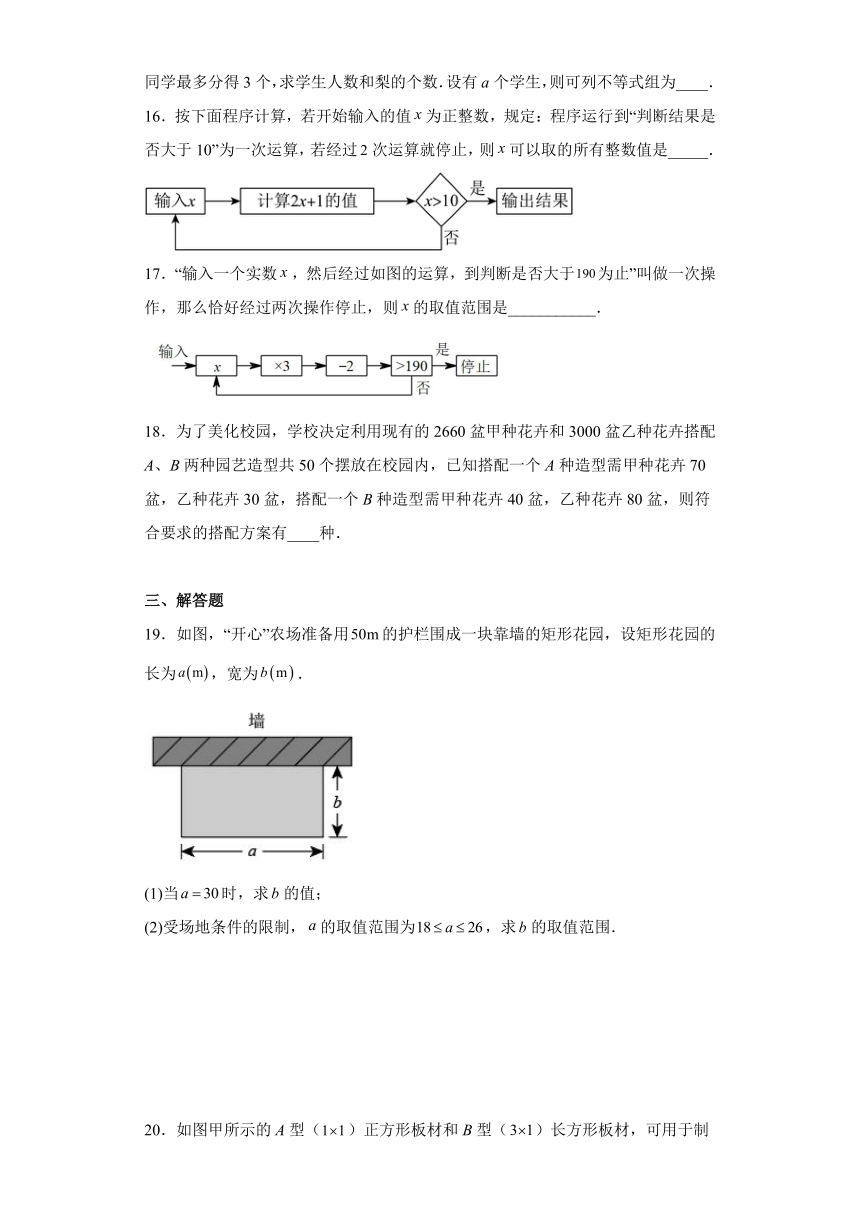
16.按下面程序计算,若开始输入的值为正整数,规定:程序运行到“判断结果是否大于10”为一次运算,若经过次运算就停止,则可以取的所有整数值是_____.
17.“输入一个实数,然后经过如图的运算,到判断是否大于为止”叫做一次操作,那么恰好经过两次操作停止,则的取值范围是___________.
18.为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆,则符合要求的搭配方案有____种.
三、解答题
19.如图,“开心”农场准备用的护栏围成一块靠墙的矩形花园,设矩形花园的长为,宽为.
(1)当时,求的值;
(2)受场地条件的限制,的取值范围为,求的取值范围.
20.如图甲所示的A型()正方形板材和B型()长方形板材,可用于制作成图乙所示的竖式和横式两种无盖箱子.已知板材每平方米20元.
(1)若用2860元的资金去购买A、B两种型号板材,并全部制作竖式箱子,问可以制作竖式箱子多少只?
(2)若有A型板材67张、B型板材135张,用这批板材制作两种类型的箱子共40只.问有哪几种制作方案?
21.学校举行八年级段数学知识竞赛,设立了一、二、三等奖,计划共购买件奖品,其中二等奖奖品件数比一等奖奖品件数的倍还少件,已知购买一等奖奖品件,各种奖品的单价如表:
奖品 一等奖奖品 二等奖奖品 三等奖奖品
单价(元)
(1)学校购买二等奖奖品 件,三等奖奖品 件;(用含的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的倍,且三等奖奖品的件数不少于一等奖奖品件数的倍.问学校共有几种购买方案?如何购买这三种奖品,使总费用最少?并求出最少的总费用.
22.夏天到了,学校计划对一些班级装空调.根据调查,买2台A型空调和4台B型空调共需资金15000元,买5台A型空调和1台B型空调共需资金14100元.
(1)A型空调和B型空调的单价分别是多少元?
(2)学校共要买8台空调.要求资金不少于19000元且不多于19600元,请问有哪些购买方案?
23.有大小两种货车,2辆大货车与3辆小货车一次可以运货,5辆大货车与6辆小货车一次可以运货.
(1)每辆大货车与每辆小货车一次分别可以运货多少吨?
(2)若每辆大货车的租金为400元,每辆小货车的租金为300元,某公司计划租用这两种货车共20辆把货物一次性运走,要使总费用不超过7000元,一共有多少种租车方案?
参考答案:
1.B
【分析】根据图形可得不等式组,解不等式组即可求解.
解:由题意得:
,
由得:,
把代入中得:,
∴,
∴,
∴,
由得:,
∴,
∴,
∴,
故选:B.
2.C
【分析】根据关键词“不超过”就是小于等于,然后列出不等式即可.
解:由题意得:0≤x≤13,
故选:C.
3.C
【分析】本题先由题意找出不等关系列出不等式组为得:,解出即可.
解:设买软件x片,磁盘y盒,x取正整数,
得:,,,
不相同的选购方式有,共6种方案.
故选:C.
4.D
【分析】根据“操作恰好进行两次就停止了”可得第一次运行的结果小于等于190,第二次运行的结果大于190,由此建立不等式组,再解不等式组即可得.
由题意得:,
解不等式①得:x≤64,
解不等式②得:x>22,
则不等式组的解集为225.C
【分析】先解不等式组求得解集,然后再根据所有整数解的和为确定m的取值范围,进而确定m的可能取值,最后求和即可.
解:
解不等式①可得:
解不等式②可得:
∴不等式组的解集为:
∵不等式组的所有整数解的和为
∴或
∴或
∴或
∴m的值为,则.
6.C
【分析】根据每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友所分苹果不到8个.由此得出不等式组.
解:根据小朋友的人数为,根据题意可得:
,
故选:C.
7.D
解:①,,停止运行,输出,正确;
②根据题意可得:,解得,x的最大值是8,正确;
③当输入为时,,,继续运行,则,
此时输出结果也为21,但是输入的数不为,错误;
④由题意可得:当时,会不停止运行,解得,正确;
正确的是①②④
8.D
【分析】若需要经过两次运算,才能运算出y,则有不等式组:,即可解出x的取值范围.
解:由输入两次,才能计算出y的值得:,解得.
9.D
【分析】设购买豆沙馅的x个,根据“两种的粽子至少各买一个,买粽子的总钱数不能超过15元”可得,解不等式组即可求出购买豆沙馅的可能个数,再结合总钱数不超过15元,蛋黄鲜肉馅的至少买一个,即可得出不同的购买方案.
解:设购买豆沙馅的x个,
根据题意列出不等式组: 解得:,
当时,,即蛋黄鲜肉馅的可以买1个、2个、3个、4个;
同理,当时,蛋黄鲜肉馅的可以买1个、2个、3个;
当时,蛋黄鲜肉馅的可以买1个、2个、3个;
当时,蛋黄鲜肉馅的可以买1个、2个;
当时,蛋黄鲜肉馅的可以买1个;
当时,蛋黄鲜肉馅的可以买1个;
因此,有(种)不同的购买方案,
10.A
【分析】设有x个帐篷,登山队有y人,依题意列出关于x,y的二元一次方程和不等式组组,再整理,解出y的取值范围即可选择.
设有x个帐篷,登山队有y人,
依题意有:,
∴,即,
解得:.
∴选项中只有A不符合题意.
故选A.
11.6
【分析】设有个小朋友,每人分5个,表示出最后一个小朋友分得的糖果数,根据最后一个小朋友能分到糖果但个数不足3个列出不等式组,解不等式组即可.
解:设有个小朋友,根据题意得:
,
解得:,
∴共有6个小朋友.
故答案为:6.
12.
【分析】根据题意得出不等式组,确定不等式组的解集即可.
解:∵A菌种生长的温度在20~28℃之间(不包括20℃、28℃),B菌种生长的温度在 25~33℃之间(不包括25℃、33℃)
∴,
∴,
故答案为:.
13.0<a<30
【分析】根据题意列出不等式组即可求解.
解:由周末略有剩余,得到不等式组:
,
解得:0<a<30.
故答案为:0<a<30.
14.
【分析】根据晨晨要晋级需超过90分,就可以得到不等关系,设晨晨同学应答对道题才能晋级,则根据不等关系就可以列出不等式求解.
设晨晨同学应答对道题才能晋级,根据题意可得,
,
∴,
∵取整数,
∴的最小为:,
故答案为:.
15.
【分析】设有a个学生,梨的总数为个,最后一个学生得到梨的个数为:,根据最后一个同学最多分得3个,即大于0个小于等于3个,列出一元一次不等式组即可求解.
解:由已知条件可得,梨的总数为个,最后一个学生得到梨的个数为:
最后一个同学最多分得3个,
则,即.
故答案为.
16.2或3或4
【分析】根据题意可列出不等式组,解不等式组可得x的所有可能取值.
解:根据题意可得:
,
由①得:,
由②得:,
,
由②得:,
∴不等式组的解集为,
∵为正整数,
∴x可以取得所有值时2或3或4,
故答案为:2或3或4.
17.
【分析】表示出第一次、第二次的输出结果,再由输出结果可得出不等式,解出即可.
解:依题意得:第一次的结果为:,没有输出,
则,解得:;
第二次的结果为:,输出,
则,解得:;
综上可得:.
故答案为:.
18.3
【分析】设可以搭配成个A种造型,则可以搭配成个B种造型,根据搭配50个园艺造型所需甲种花卉不超过2660盆、乙种花卉不超过3000盆,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再结合x为整数,即可得出符合要求的搭配方案有3种.
解:设可以搭配成个A种造型,则可以搭配成个B种造型,
依题意得:,
解得:.
又∵x为整数,
∴x可以为20,21,22,
∴符合要求的搭配方案有3种.
故答案为:3.
19.(1)10;
(2).
【分析】(1)根据等量关系“围栏的长度为50”可以列出代数式,再将a=30代入所列式子中求出b的值;
(2)由(1)可得a,b之间的关系式,用含有b的式子表示a,再结合,列出关于b的不等式组,解不等式组即可求出b的取值范围.
(1)
解:由题意,得,
当时,.
解得.
(2)
解:∵,
∴,
,
∴
解这个不等式组,得.
答:矩形花园宽的取值范围为.
20.(1)11
(2)3种方案,①制作竖式箱子13只,横式箱子27只;②制作竖式箱子14只,横式箱子26只;③制作竖式箱子15只,横式箱子25只
【分析】(1)设购买A型板材x张,购买B型板材y张,则可制作竖式无盖箱子x只,由题意:用2860元的资金去购买A、B两种型号板材,并全部制作竖式箱子,列出二元一次方程组,解方程组即可;
(2)设制作竖式箱子a只,横式箱子b只,由题意:有A型板材67张、B型板材135张,用这批板材制作两种类型的箱子共40只,列出一元一次不等式组,解得,即可解决问题.
(1)解∶∵板材每平方米20元,
∴A型板材每张20元,B型板材每张(元),
设购买A型板材x张,购买B型板材y张,则可制作竖式无盖箱子x只,
由题意得:
,
解得:,
答:可以制作竖式箱子11只;
(2)解:设制作竖式箱子a只,横式箱子b只,
则,
由题意得:,
解得:,
∵a为正整数,
∴或或,则或或,∴有3种制作方案:
①制作竖式箱子13只,横式箱子27只;
②制作竖式箱子14只,横式箱子26只;
③制作竖式箱子15只,横式箱子25只.
21.(1);
(2)共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元
【分析】(1)根据一等奖奖品件及二等奖奖品件数比一等奖奖品件数的倍还少件,可得二等奖奖品件,由计划共购买件奖品,可得三等奖奖品件;
(2)根据题意列出不等式组,解出的取值范围,由为正整数,可得或,即共有两种购买方案,设总运费为,得出,分别求出当和时的总运费,比较选出运费最少的,并求出此时每种奖品的件数即可.
(1)解:学校购买二等奖奖品件,三等奖奖品件;
故答案为:;.
(2)解:根据题意可得:,
解得,
∵为正整数,
∴或,
设总费用为,则,
当时,(元),
当时,(元).
∴共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元.
22.(1)A型空调每台需2300元,B型空调每台需2600元
(2)有三种采购方案:方案一:采购4台A型空调,4台B型空调;方案二:采购5台A型空调,3台B型空调;方案三:采购6台A型空调,2台B型空调.
【分析】(1)根据“采购2台A型空调和4台B型空调,共需费用15000元;5台A型空调和1台B型空调,共需费用14100元”可以列出相应的方程组,从而可以解答本题;
(2)根据题意可以列出相应的不等式组,从而可以求得有几种采购方案.
(1)
解:设A型空调每台需x元,B型空调每台需y元.
由题意可列:,
解得,
答:A型空调每台需2300元,B型空调每台需2600元.
(2)解:设采购A型空调m台,则采购B型空调(8-m)台,
由题意可列:,
解得,
∵m为正整数,
∴m=4,5,6.
∴有三种采购方案:
方案一:采购4台A型空调,4台B型空调;
方案二:采购5台A型空调,3台B型空调;
方案三:采购6台A型空调,2台B型空调.
23.(1)每辆大货车与每辆小货车一次分别可以运货4吨和2.5吨
(2)一共有4种租车方案
【分析】(1)设1辆大货车和1辆小货车一次可以分别运货x吨和y吨,根据“2辆大货车与3辆小货车一次可以运货15.5t,5辆大货车与6辆小货车一次可以运货35t”列方程组求解可得;
(2)设租用大货车z辆,由运输60吨且用20辆车一次运完,总运费不超过7000元,列出不等式组,求得不等式的整数解的个数便可得出答案.
(1)
设每辆大货车与每辆小货车一次分别可以运货吨和吨,依题意,得
,
解得:,
答:每辆大货车与每辆小货车一次分别可以运货4吨和2.5吨.
(2)设租用大货车辆,则租用小货车辆,依题意,得
,
解得:,
∵为整数,
∴,8,9,10,
∴一共有4种租车方案.
一、单选题
1.、、、四人去玩跷跷板,由下面示意图,判断这四人轻重正确的是( )
A. B. C. D.
2.某电梯标明“载客不超过13人”,设载客人数为x(x为自然数),则“载客不超过13人”用不等式表示为 ( )
A.0<x<13 B.1≤x≤13 C.0≤x≤13 D.x≥13
3.某电脑用户使用不超过530元资金购买单价为70元的单片软件和80元的盒装磁带,根据需要,软件至少买3片,磁盘至少买2盒,则不相同的购买方式共有( )
A.4 种 B.5 种 C.6 种 D.7 种
4.对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次就停止了,那么x的取值范围是( )
A.8<x≤22 B.8≤x<22 C.8<x≤64 D.22<x≤64
5.已知关于x的不等式组的所有整数解的和为,满足条件的所有整数m的和是( )
A.13 B.-15 C.-2 D.0
6.将一箱苹果分给若干个学生,每个学生都分到苹果.若每个学生分5个苹果,则还剩12个苹果;若每位学生分8个苹果,则有一个学生所分苹果不足8个.若学生的人数为,则列式正确的是( )
A. B.
C. D.
7.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,①输入整数11,输出结果为27;②若输入整数x后程序操作仅进行了两次就停止,则x的最大值是8;③若操作停止时输出结果为21,则输入的整数x是9;④输入整数x后,该操作永不停止,则,以上结论正确有( )
A.①② B.①②③ C.①③④ D.①②④
8.如图,是一个运算流程,若需要经过两次运算,才能运算出,则的取值范围是( )
A. B. C. D.
9.五月初五端午节这天,妈妈让小明去超市买豆沙馅和蛋黄鲜肉馅的粽子.豆沙馅的每个卖2元,蛋黄鲜肉馅的每个卖3元,两种的粽子至少各买一个,买粽子的总钱数不能超过15元.则不同的购买方案的个数为( )
A.11 B.12 C.13 D.14
10.某登山队在野外露营,每个帐篷住5人,有3人没地方住,若每个帐篷住7人,则空出一个帐篷,还有一个帐篷不空.那么这个登山队不可能有( )人.
A.23 B.28 C.33 D.38
二、填空题
11.有若干糖果要分给小朋友,若每人分3个,则余8个;每人分5个,则最后一个小朋友能分到糖果但个数不足3个,则共有________个小朋友.
12.某生物兴趣小组要在恒温箱中培养A,B两种菌种,A菌种生长的温度在20~28℃之间(不包括20℃、28℃),B菌种生长的温度在 25~33℃之间(不包括25℃、33℃),若设恒温箱的温度为t℃,则t所满足的不等式为_______.
13.七年级学生张明的母亲给他150元钱,作为他一周在校五天的生活费,假定张明平均每天所用的生活费为a元,且到周末略有剩余,则a的取值范围是_________.
14.海口市某中学举行党史知识竞赛.竞赛共有20道题,规定答对一道题得10分,答错或不答扣5分,本次竞赛中晨晨同学要超过90分才能晋级,则她至少答对__________道题.
15.把一筐梨分给几个学生,若每人4个,则剩下3个;若每人6个,则最后一个同学最多分得3个,求学生人数和梨的个数.设有a个学生,则可列不等式组为____.
16.按下面程序计算,若开始输入的值为正整数,规定:程序运行到“判断结果是否大于10”为一次运算,若经过次运算就停止,则可以取的所有整数值是_____.
17.“输入一个实数,然后经过如图的运算,到判断是否大于为止”叫做一次操作,那么恰好经过两次操作停止,则的取值范围是___________.
18.为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆,则符合要求的搭配方案有____种.
三、解答题
19.如图,“开心”农场准备用的护栏围成一块靠墙的矩形花园,设矩形花园的长为,宽为.
(1)当时,求的值;
(2)受场地条件的限制,的取值范围为,求的取值范围.
20.如图甲所示的A型()正方形板材和B型()长方形板材,可用于制作成图乙所示的竖式和横式两种无盖箱子.已知板材每平方米20元.
(1)若用2860元的资金去购买A、B两种型号板材,并全部制作竖式箱子,问可以制作竖式箱子多少只?
(2)若有A型板材67张、B型板材135张,用这批板材制作两种类型的箱子共40只.问有哪几种制作方案?
21.学校举行八年级段数学知识竞赛,设立了一、二、三等奖,计划共购买件奖品,其中二等奖奖品件数比一等奖奖品件数的倍还少件,已知购买一等奖奖品件,各种奖品的单价如表:
奖品 一等奖奖品 二等奖奖品 三等奖奖品
单价(元)
(1)学校购买二等奖奖品 件,三等奖奖品 件;(用含的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的倍,且三等奖奖品的件数不少于一等奖奖品件数的倍.问学校共有几种购买方案?如何购买这三种奖品,使总费用最少?并求出最少的总费用.
22.夏天到了,学校计划对一些班级装空调.根据调查,买2台A型空调和4台B型空调共需资金15000元,买5台A型空调和1台B型空调共需资金14100元.
(1)A型空调和B型空调的单价分别是多少元?
(2)学校共要买8台空调.要求资金不少于19000元且不多于19600元,请问有哪些购买方案?
23.有大小两种货车,2辆大货车与3辆小货车一次可以运货,5辆大货车与6辆小货车一次可以运货.
(1)每辆大货车与每辆小货车一次分别可以运货多少吨?
(2)若每辆大货车的租金为400元,每辆小货车的租金为300元,某公司计划租用这两种货车共20辆把货物一次性运走,要使总费用不超过7000元,一共有多少种租车方案?
参考答案:
1.B
【分析】根据图形可得不等式组,解不等式组即可求解.
解:由题意得:
,
由得:,
把代入中得:,
∴,
∴,
∴,
由得:,
∴,
∴,
∴,
故选:B.
2.C
【分析】根据关键词“不超过”就是小于等于,然后列出不等式即可.
解:由题意得:0≤x≤13,
故选:C.
3.C
【分析】本题先由题意找出不等关系列出不等式组为得:,解出即可.
解:设买软件x片,磁盘y盒,x取正整数,
得:,,,
不相同的选购方式有,共6种方案.
故选:C.
4.D
【分析】根据“操作恰好进行两次就停止了”可得第一次运行的结果小于等于190,第二次运行的结果大于190,由此建立不等式组,再解不等式组即可得.
由题意得:,
解不等式①得:x≤64,
解不等式②得:x>22,
则不等式组的解集为22
【分析】先解不等式组求得解集,然后再根据所有整数解的和为确定m的取值范围,进而确定m的可能取值,最后求和即可.
解:
解不等式①可得:
解不等式②可得:
∴不等式组的解集为:
∵不等式组的所有整数解的和为
∴或
∴或
∴或
∴m的值为,则.
6.C
【分析】根据每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友所分苹果不到8个.由此得出不等式组.
解:根据小朋友的人数为,根据题意可得:
,
故选:C.
7.D
解:①,,停止运行,输出,正确;
②根据题意可得:,解得,x的最大值是8,正确;
③当输入为时,,,继续运行,则,
此时输出结果也为21,但是输入的数不为,错误;
④由题意可得:当时,会不停止运行,解得,正确;
正确的是①②④
8.D
【分析】若需要经过两次运算,才能运算出y,则有不等式组:,即可解出x的取值范围.
解:由输入两次,才能计算出y的值得:,解得.
9.D
【分析】设购买豆沙馅的x个,根据“两种的粽子至少各买一个,买粽子的总钱数不能超过15元”可得,解不等式组即可求出购买豆沙馅的可能个数,再结合总钱数不超过15元,蛋黄鲜肉馅的至少买一个,即可得出不同的购买方案.
解:设购买豆沙馅的x个,
根据题意列出不等式组: 解得:,
当时,,即蛋黄鲜肉馅的可以买1个、2个、3个、4个;
同理,当时,蛋黄鲜肉馅的可以买1个、2个、3个;
当时,蛋黄鲜肉馅的可以买1个、2个、3个;
当时,蛋黄鲜肉馅的可以买1个、2个;
当时,蛋黄鲜肉馅的可以买1个;
当时,蛋黄鲜肉馅的可以买1个;
因此,有(种)不同的购买方案,
10.A
【分析】设有x个帐篷,登山队有y人,依题意列出关于x,y的二元一次方程和不等式组组,再整理,解出y的取值范围即可选择.
设有x个帐篷,登山队有y人,
依题意有:,
∴,即,
解得:.
∴选项中只有A不符合题意.
故选A.
11.6
【分析】设有个小朋友,每人分5个,表示出最后一个小朋友分得的糖果数,根据最后一个小朋友能分到糖果但个数不足3个列出不等式组,解不等式组即可.
解:设有个小朋友,根据题意得:
,
解得:,
∴共有6个小朋友.
故答案为:6.
12.
【分析】根据题意得出不等式组,确定不等式组的解集即可.
解:∵A菌种生长的温度在20~28℃之间(不包括20℃、28℃),B菌种生长的温度在 25~33℃之间(不包括25℃、33℃)
∴,
∴,
故答案为:.
13.0<a<30
【分析】根据题意列出不等式组即可求解.
解:由周末略有剩余,得到不等式组:
,
解得:0<a<30.
故答案为:0<a<30.
14.
【分析】根据晨晨要晋级需超过90分,就可以得到不等关系,设晨晨同学应答对道题才能晋级,则根据不等关系就可以列出不等式求解.
设晨晨同学应答对道题才能晋级,根据题意可得,
,
∴,
∵取整数,
∴的最小为:,
故答案为:.
15.
【分析】设有a个学生,梨的总数为个,最后一个学生得到梨的个数为:,根据最后一个同学最多分得3个,即大于0个小于等于3个,列出一元一次不等式组即可求解.
解:由已知条件可得,梨的总数为个,最后一个学生得到梨的个数为:
最后一个同学最多分得3个,
则,即.
故答案为.
16.2或3或4
【分析】根据题意可列出不等式组,解不等式组可得x的所有可能取值.
解:根据题意可得:
,
由①得:,
由②得:,
,
由②得:,
∴不等式组的解集为,
∵为正整数,
∴x可以取得所有值时2或3或4,
故答案为:2或3或4.
17.
【分析】表示出第一次、第二次的输出结果,再由输出结果可得出不等式,解出即可.
解:依题意得:第一次的结果为:,没有输出,
则,解得:;
第二次的结果为:,输出,
则,解得:;
综上可得:.
故答案为:.
18.3
【分析】设可以搭配成个A种造型,则可以搭配成个B种造型,根据搭配50个园艺造型所需甲种花卉不超过2660盆、乙种花卉不超过3000盆,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再结合x为整数,即可得出符合要求的搭配方案有3种.
解:设可以搭配成个A种造型,则可以搭配成个B种造型,
依题意得:,
解得:.
又∵x为整数,
∴x可以为20,21,22,
∴符合要求的搭配方案有3种.
故答案为:3.
19.(1)10;
(2).
【分析】(1)根据等量关系“围栏的长度为50”可以列出代数式,再将a=30代入所列式子中求出b的值;
(2)由(1)可得a,b之间的关系式,用含有b的式子表示a,再结合,列出关于b的不等式组,解不等式组即可求出b的取值范围.
(1)
解:由题意,得,
当时,.
解得.
(2)
解:∵,
∴,
,
∴
解这个不等式组,得.
答:矩形花园宽的取值范围为.
20.(1)11
(2)3种方案,①制作竖式箱子13只,横式箱子27只;②制作竖式箱子14只,横式箱子26只;③制作竖式箱子15只,横式箱子25只
【分析】(1)设购买A型板材x张,购买B型板材y张,则可制作竖式无盖箱子x只,由题意:用2860元的资金去购买A、B两种型号板材,并全部制作竖式箱子,列出二元一次方程组,解方程组即可;
(2)设制作竖式箱子a只,横式箱子b只,由题意:有A型板材67张、B型板材135张,用这批板材制作两种类型的箱子共40只,列出一元一次不等式组,解得,即可解决问题.
(1)解∶∵板材每平方米20元,
∴A型板材每张20元,B型板材每张(元),
设购买A型板材x张,购买B型板材y张,则可制作竖式无盖箱子x只,
由题意得:
,
解得:,
答:可以制作竖式箱子11只;
(2)解:设制作竖式箱子a只,横式箱子b只,
则,
由题意得:,
解得:,
∵a为正整数,
∴或或,则或或,∴有3种制作方案:
①制作竖式箱子13只,横式箱子27只;
②制作竖式箱子14只,横式箱子26只;
③制作竖式箱子15只,横式箱子25只.
21.(1);
(2)共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元
【分析】(1)根据一等奖奖品件及二等奖奖品件数比一等奖奖品件数的倍还少件,可得二等奖奖品件,由计划共购买件奖品,可得三等奖奖品件;
(2)根据题意列出不等式组,解出的取值范围,由为正整数,可得或,即共有两种购买方案,设总运费为,得出,分别求出当和时的总运费,比较选出运费最少的,并求出此时每种奖品的件数即可.
(1)解:学校购买二等奖奖品件,三等奖奖品件;
故答案为:;.
(2)解:根据题意可得:,
解得,
∵为正整数,
∴或,
设总费用为,则,
当时,(元),
当时,(元).
∴共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元.
22.(1)A型空调每台需2300元,B型空调每台需2600元
(2)有三种采购方案:方案一:采购4台A型空调,4台B型空调;方案二:采购5台A型空调,3台B型空调;方案三:采购6台A型空调,2台B型空调.
【分析】(1)根据“采购2台A型空调和4台B型空调,共需费用15000元;5台A型空调和1台B型空调,共需费用14100元”可以列出相应的方程组,从而可以解答本题;
(2)根据题意可以列出相应的不等式组,从而可以求得有几种采购方案.
(1)
解:设A型空调每台需x元,B型空调每台需y元.
由题意可列:,
解得,
答:A型空调每台需2300元,B型空调每台需2600元.
(2)解:设采购A型空调m台,则采购B型空调(8-m)台,
由题意可列:,
解得,
∵m为正整数,
∴m=4,5,6.
∴有三种采购方案:
方案一:采购4台A型空调,4台B型空调;
方案二:采购5台A型空调,3台B型空调;
方案三:采购6台A型空调,2台B型空调.
23.(1)每辆大货车与每辆小货车一次分别可以运货4吨和2.5吨
(2)一共有4种租车方案
【分析】(1)设1辆大货车和1辆小货车一次可以分别运货x吨和y吨,根据“2辆大货车与3辆小货车一次可以运货15.5t,5辆大货车与6辆小货车一次可以运货35t”列方程组求解可得;
(2)设租用大货车z辆,由运输60吨且用20辆车一次运完,总运费不超过7000元,列出不等式组,求得不等式的整数解的个数便可得出答案.
(1)
设每辆大货车与每辆小货车一次分别可以运货吨和吨,依题意,得
,
解得:,
答:每辆大货车与每辆小货车一次分别可以运货4吨和2.5吨.
(2)设租用大货车辆,则租用小货车辆,依题意,得
,
解得:,
∵为整数,
∴,8,9,10,
∴一共有4种租车方案.
