2022--2023学年北师大版九年级数学下册1.4 解直角三角形 巩固复习(无答案)
文档属性
| 名称 | 2022--2023学年北师大版九年级数学下册1.4 解直角三角形 巩固复习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 162.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 15:04:28 | ||
图片预览

文档简介
1.4 解直角三角形(巩固复习)-北师大版九年级下册
一.选择题
.如图,在Rt△ABC中,∠ACB=90°,过点D作DE⊥AB交AC于点E,若S△ADE=,sin∠CDE=,则BC的长为( )
A.5 B. C. D.
.在平面直角坐标系xOy中,已知点P(1,3)与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°)( )
A.3 B. C. D.
.在△ABC中,已知AC=3,BC=4,那么下列结论正确的是( )
A.sinA= B.cosA=
C.tanA= D.以上均不正确
.如图,已知点P(4,3),OP与x轴正半轴的夹角为α( )
A. B. C. D.
.如图,某博物馆大厅电梯的截面图中,AB的长为12米,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
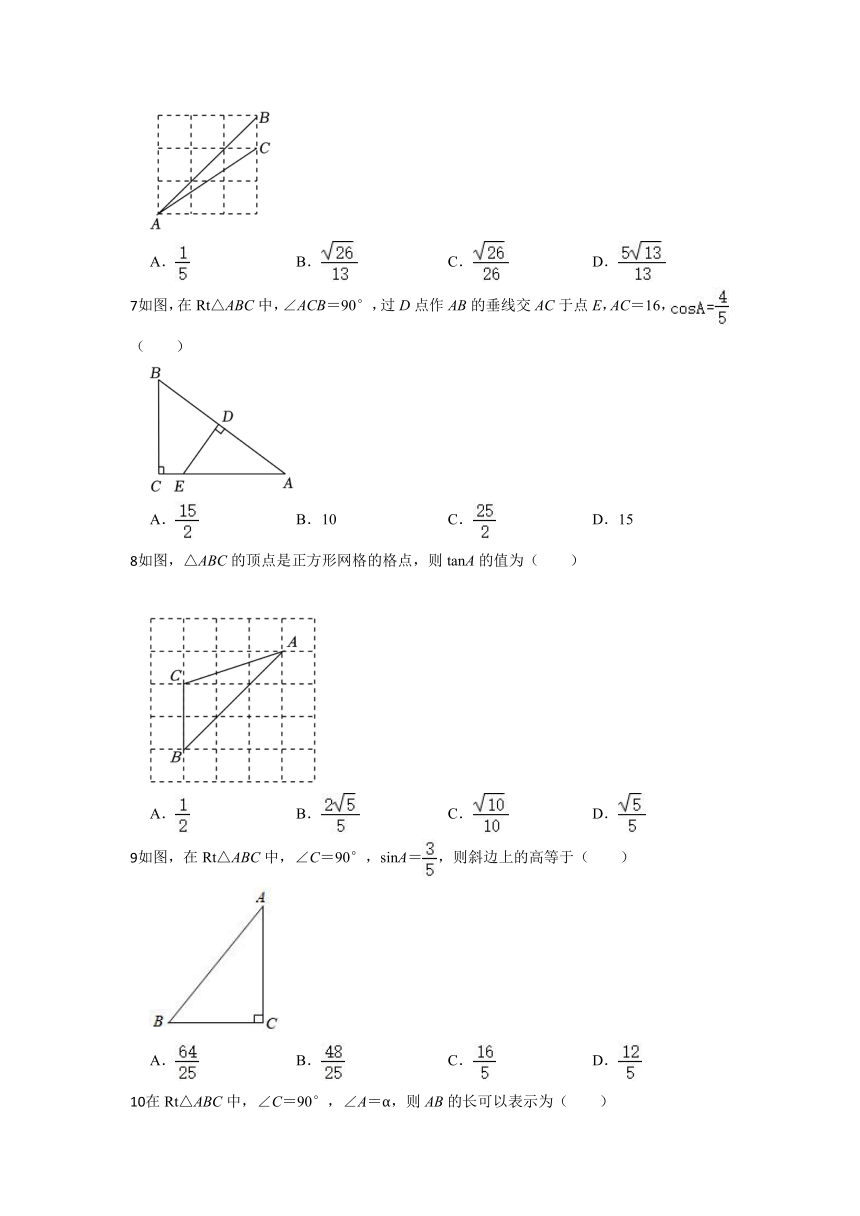
如图,A,B,C是正方形网格的格点,连接AC,则tan∠BAC的值是( )
A. B. C. D.
如图,在Rt△ABC中,∠ACB=90°,过D点作AB的垂线交AC于点E,AC=16,( )
A. B.10 C. D.15
如图,△ABC的顶点是正方形网格的格点,则tanA的值为( )
A. B. C. D.
如图,在Rt△ABC中,∠C=90°,sinA=,则斜边上的高等于( )
A. B. C. D.
在Rt△ABC中,∠C=90°,∠A=α,则AB的长可以表示为( )
A. B. C.b sinα D.b cosα
二.填空题
.如图,直线OA过点(4,3),则tanα= .
.在Rt△ABC中,∠C=90°,sinA=,那么BC的长是 .
.如图,在平面直角坐标系xOy中,AB=,连结OC,若满足OC2=BC AC,tanα=3,则点C的坐标为 .
.在△ABC中,AB=8,BC=6,则△ABC的面积等于 .
.如图所示,在四边形ABCD中,CD=10,M为AD中点,动点P从点B出发沿BC向终点C运动,DP,取AP中点N,求线段MN的最小值 .
三.解答题
.(1)如图甲,已知:在△ABC中,∠A=30°,AC=4,求AB;
(2)如图乙,已知:在△ABC中,∠A=45°,AC=1,求AB.
.如图,在Rt△ABC中,已知∠C=90°.
(1)在AB边上求作点D,连接CD、使得∠CDB=2∠A;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图形中,当AB=10,求sin∠CDB的值.
.如图,点P是∠α的边OA上的一点,已知点P的横坐标为6.
(1)求点P的纵坐标;
(2)求∠α的正弦值、余弦值.
.(1)若a,b,c,d是实数,我们规定,当时
(2)如图,在平面直角坐标系内,O为原点,点B的坐标为(4,3).若tan∠BAO=sin∠BOA
.如图,在△ABC中,sin∠BAC=,AC=7.2,BD⊥AC,点E是BD的中点,AE与BC交于点F.
(1)求:∠CBD的正切;
(2)求的值.
一.选择题
.如图,在Rt△ABC中,∠ACB=90°,过点D作DE⊥AB交AC于点E,若S△ADE=,sin∠CDE=,则BC的长为( )
A.5 B. C. D.
.在平面直角坐标系xOy中,已知点P(1,3)与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°)( )
A.3 B. C. D.
.在△ABC中,已知AC=3,BC=4,那么下列结论正确的是( )
A.sinA= B.cosA=
C.tanA= D.以上均不正确
.如图,已知点P(4,3),OP与x轴正半轴的夹角为α( )
A. B. C. D.
.如图,某博物馆大厅电梯的截面图中,AB的长为12米,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
如图,A,B,C是正方形网格的格点,连接AC,则tan∠BAC的值是( )
A. B. C. D.
如图,在Rt△ABC中,∠ACB=90°,过D点作AB的垂线交AC于点E,AC=16,( )
A. B.10 C. D.15
如图,△ABC的顶点是正方形网格的格点,则tanA的值为( )
A. B. C. D.
如图,在Rt△ABC中,∠C=90°,sinA=,则斜边上的高等于( )
A. B. C. D.
在Rt△ABC中,∠C=90°,∠A=α,则AB的长可以表示为( )
A. B. C.b sinα D.b cosα
二.填空题
.如图,直线OA过点(4,3),则tanα= .
.在Rt△ABC中,∠C=90°,sinA=,那么BC的长是 .
.如图,在平面直角坐标系xOy中,AB=,连结OC,若满足OC2=BC AC,tanα=3,则点C的坐标为 .
.在△ABC中,AB=8,BC=6,则△ABC的面积等于 .
.如图所示,在四边形ABCD中,CD=10,M为AD中点,动点P从点B出发沿BC向终点C运动,DP,取AP中点N,求线段MN的最小值 .
三.解答题
.(1)如图甲,已知:在△ABC中,∠A=30°,AC=4,求AB;
(2)如图乙,已知:在△ABC中,∠A=45°,AC=1,求AB.
.如图,在Rt△ABC中,已知∠C=90°.
(1)在AB边上求作点D,连接CD、使得∠CDB=2∠A;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图形中,当AB=10,求sin∠CDB的值.
.如图,点P是∠α的边OA上的一点,已知点P的横坐标为6.
(1)求点P的纵坐标;
(2)求∠α的正弦值、余弦值.
.(1)若a,b,c,d是实数,我们规定,当时
(2)如图,在平面直角坐标系内,O为原点,点B的坐标为(4,3).若tan∠BAO=sin∠BOA
.如图,在△ABC中,sin∠BAC=,AC=7.2,BD⊥AC,点E是BD的中点,AE与BC交于点F.
(1)求:∠CBD的正切;
(2)求的值.
