第17章 勾股定理 专题课件(20张ppt)
文档属性
| 名称 | 第17章 勾股定理 专题课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-26 18:10:38 | ||
图片预览



文档简介
(共20张PPT)
勾股定理--最短路径
人教版八年级下册
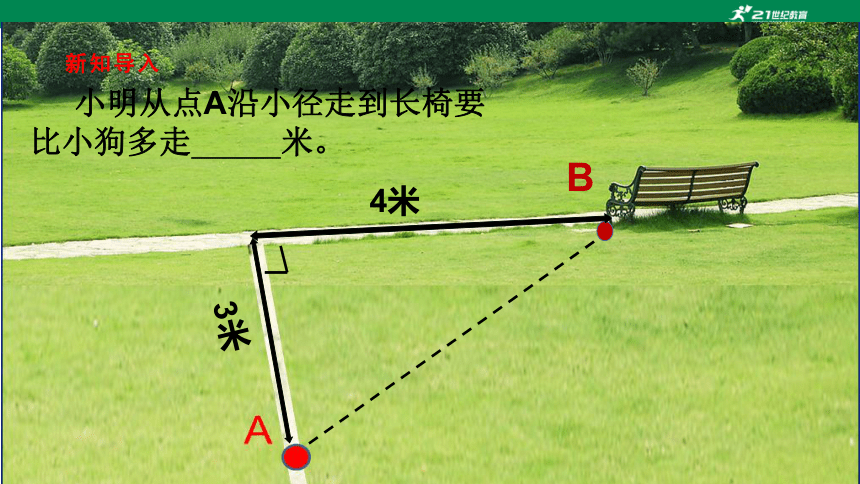
新知导入
B
3米
4米
小明从点A沿小径走到长椅要比小狗多走 米。
新知讲解
问题:
勾股定理
两点之间,线段最短
实际问题
平面几何
1、小狗从点A到B的最短距离时什么 依据是什么?
2、小狗走的距离是多少?怎么计算?依据是什么?
3、这个问题研究的过程是什么?
新知讲解
平面中的最短路线很容易就可以找见,并运用勾股定理求得,那么在立体图形中呢?
新知讲解
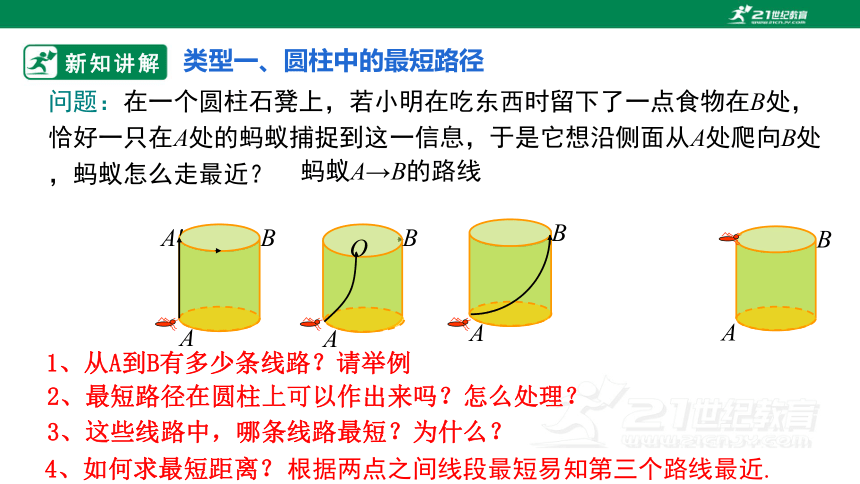
1、从A到B有多少条线路?请举例
4、如何求最短距离?
3、这些线路中,哪条线路最短?为什么?
2、最短路径在圆柱上可以作出来吗?怎么处理?
A
B
A'
A
B
B
A
O
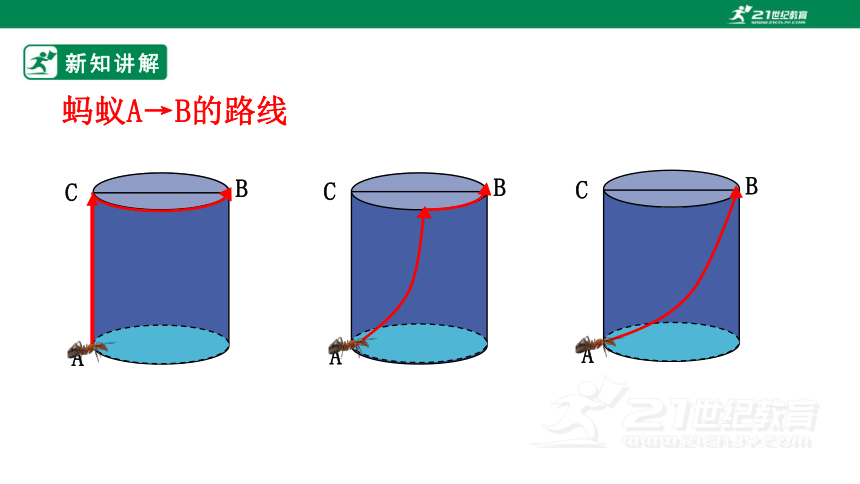
蚂蚁A→B的路线
问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想沿侧面从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第三个路线最近.
类型一、圆柱中的最短路径
新知讲解
A
C
B
A
C
B
A
C
B
蚂蚁A→B的路线
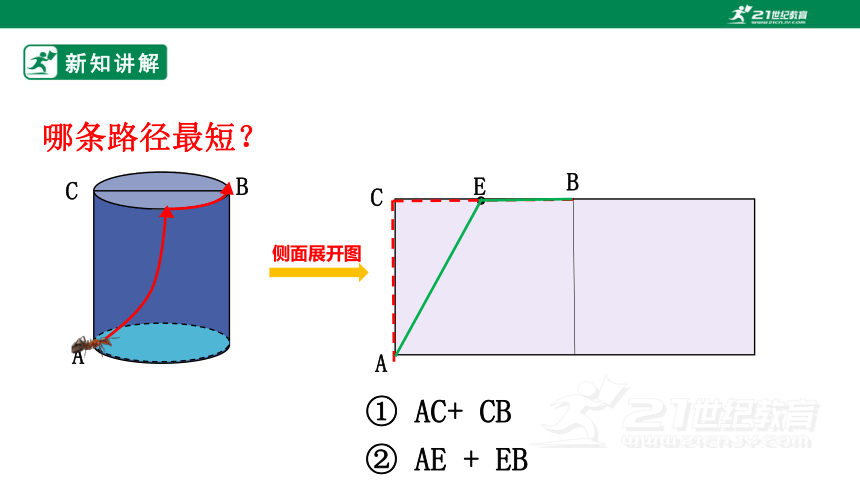
新知讲解
A
C
B
E
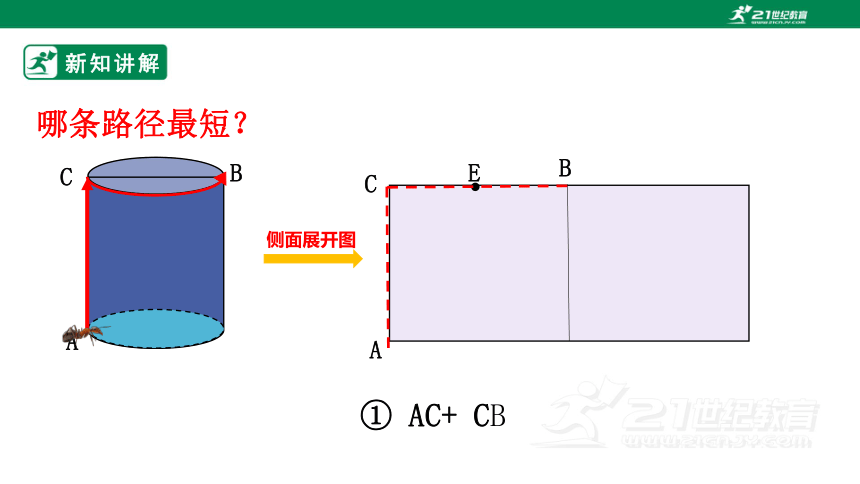
① AC+ CB
哪条路径最短?
侧面展开图
A
C
B
新知讲解
A
C
B
E
① AC+ CB
② AE + EB
哪条路径最短?
侧面展开图
A
C
B
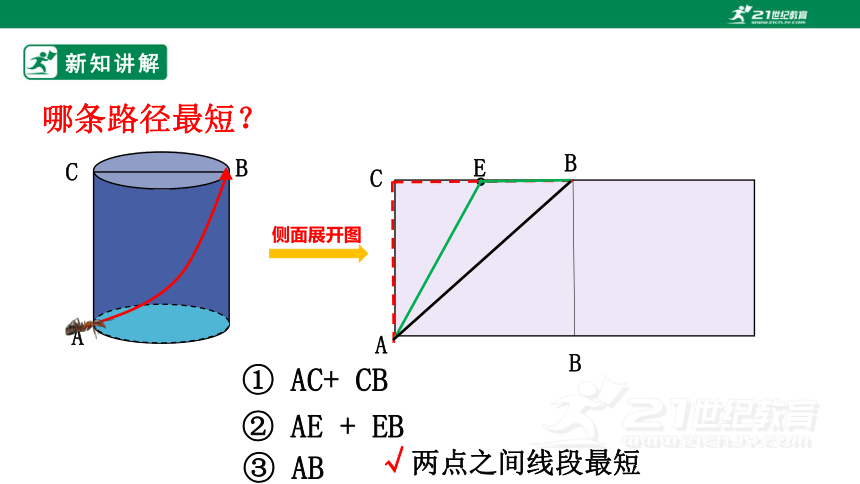
新知讲解
A
B
C
B
E
① AC+ CB
② AE + EB
③ AB
√两点之间线段最短
哪条路径最短?
侧面展开图
A
C
B
新知讲解
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
新知讲解
总结
求法:
3、利用勾股定理计算
2、构造直角三角形
1、将圆柱体的侧面展开将立体图形转化为平面图形
你能总结出圆柱体表面两点间最短距离的求法吗?
直角三角形
转化
建模
立体图形
平面图形
变式练习
1 如图,一个圆柱形油罐,要从A点环绕油罐建梯子,正好到A点的正上方B点,请你算一算梯子最短需多少米?(已知油罐的底面周长是12米,高是5米)
解:如图,将油罐侧面展开,
变式练习
2 如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为________
典例讲解
例 如图所示的长方体的高为8 cm,底面是长为10 cm,宽为6 cm的长方形.一只蚂蚁从顶点A出发沿长方体的表面爬到顶点B.求:
(1)蚂蚁经过的最短路程;
(1)蚂蚁爬行的最短路线可放在平面内,根据“两点之间,
线段最短”去探求,而与顶点A,B相关的两个面展开共
有三种方式,先根据勾股定理求出每一种方式下蚂蚁
爬行的最短路程,从而可知蚂蚁经过的最短路程.
导引:
类型二、长方体中的最短路径
典例讲解
B
B1
8
A
B2
6
10
B3
AB12 =102 +(6+8)2 =296,
AB22= 82 +(10+6)2 =320,
AB32= 62 +(10+8)2 =360,
解:由题意知有三种展开方法,如图.由勾股定理,得
∴AB1<AB2<AB3.
∴小蚂蚁完成任务的最短路程为AB1,长为 .
变式练习
3. 如图,长方体的长为15,宽为10,高为20,点B离点C
的距离为5,一只蚂蚁如果要沿着长方体的表面从点A
爬到点B,需要爬行的最短距离是( )
A.5 B.25
C.10 +5 D.35
B
典例讲解
例 如图是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
解:台阶的展开图如图,连接AB.
在Rt△ABC中,根据勾股定理得
AB2=BC2+AC2=552+482=5329,
∴AB=73cm.
类型三、台阶中的最短路径
课堂总结
1、本节课研究问题的过程是什么
2、解决上述问题运用了什么知识
3、在解决问题的过程运用了什么方法
4、运用上述方法的目的是什么 体现了什么样的数学思想
归纳总结
直角三角形
转化
建模
立体图形
平面图形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
勾股定理--最短路径
人教版八年级下册
新知导入
B
3米
4米
小明从点A沿小径走到长椅要比小狗多走 米。
新知讲解
问题:
勾股定理
两点之间,线段最短
实际问题
平面几何
1、小狗从点A到B的最短距离时什么 依据是什么?
2、小狗走的距离是多少?怎么计算?依据是什么?
3、这个问题研究的过程是什么?
新知讲解
平面中的最短路线很容易就可以找见,并运用勾股定理求得,那么在立体图形中呢?
新知讲解
1、从A到B有多少条线路?请举例
4、如何求最短距离?
3、这些线路中,哪条线路最短?为什么?
2、最短路径在圆柱上可以作出来吗?怎么处理?
A
B
A'
A
B
B
A
O
蚂蚁A→B的路线
问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想沿侧面从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第三个路线最近.
类型一、圆柱中的最短路径
新知讲解
A
C
B
A
C
B
A
C
B
蚂蚁A→B的路线
新知讲解
A
C
B
E
① AC+ CB
哪条路径最短?
侧面展开图
A
C
B
新知讲解
A
C
B
E
① AC+ CB
② AE + EB
哪条路径最短?
侧面展开图
A
C
B
新知讲解
A
B
C
B
E
① AC+ CB
② AE + EB
③ AB
√两点之间线段最短
哪条路径最短?
侧面展开图
A
C
B
新知讲解
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
归纳:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
新知讲解
总结
求法:
3、利用勾股定理计算
2、构造直角三角形
1、将圆柱体的侧面展开将立体图形转化为平面图形
你能总结出圆柱体表面两点间最短距离的求法吗?
直角三角形
转化
建模
立体图形
平面图形
变式练习
1 如图,一个圆柱形油罐,要从A点环绕油罐建梯子,正好到A点的正上方B点,请你算一算梯子最短需多少米?(已知油罐的底面周长是12米,高是5米)
解:如图,将油罐侧面展开,
变式练习
2 如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为________
典例讲解
例 如图所示的长方体的高为8 cm,底面是长为10 cm,宽为6 cm的长方形.一只蚂蚁从顶点A出发沿长方体的表面爬到顶点B.求:
(1)蚂蚁经过的最短路程;
(1)蚂蚁爬行的最短路线可放在平面内,根据“两点之间,
线段最短”去探求,而与顶点A,B相关的两个面展开共
有三种方式,先根据勾股定理求出每一种方式下蚂蚁
爬行的最短路程,从而可知蚂蚁经过的最短路程.
导引:
类型二、长方体中的最短路径
典例讲解
B
B1
8
A
B2
6
10
B3
AB12 =102 +(6+8)2 =296,
AB22= 82 +(10+6)2 =320,
AB32= 62 +(10+8)2 =360,
解:由题意知有三种展开方法,如图.由勾股定理,得
∴AB1<AB2<AB3.
∴小蚂蚁完成任务的最短路程为AB1,长为 .
变式练习
3. 如图,长方体的长为15,宽为10,高为20,点B离点C
的距离为5,一只蚂蚁如果要沿着长方体的表面从点A
爬到点B,需要爬行的最短距离是( )
A.5 B.25
C.10 +5 D.35
B
典例讲解
例 如图是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
解:台阶的展开图如图,连接AB.
在Rt△ABC中,根据勾股定理得
AB2=BC2+AC2=552+482=5329,
∴AB=73cm.
类型三、台阶中的最短路径
课堂总结
1、本节课研究问题的过程是什么
2、解决上述问题运用了什么知识
3、在解决问题的过程运用了什么方法
4、运用上述方法的目的是什么 体现了什么样的数学思想
归纳总结
直角三角形
转化
建模
立体图形
平面图形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
