5.4.3抛体运动的规律——平抛运动与圆相结合 高一下学期物理人教版(2019)必修第二册(22页ppt)
文档属性
| 名称 | 5.4.3抛体运动的规律——平抛运动与圆相结合 高一下学期物理人教版(2019)必修第二册(22页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-26 21:38:32 | ||
图片预览





文档简介
5.4.3 平抛与圆结合专题
第五章 抛体运动
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
复习导入
平抛
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
x=v0tcos?
vx=v0cos?
vy=v0sin? - gt
Part 01
平抛与圆相结合
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
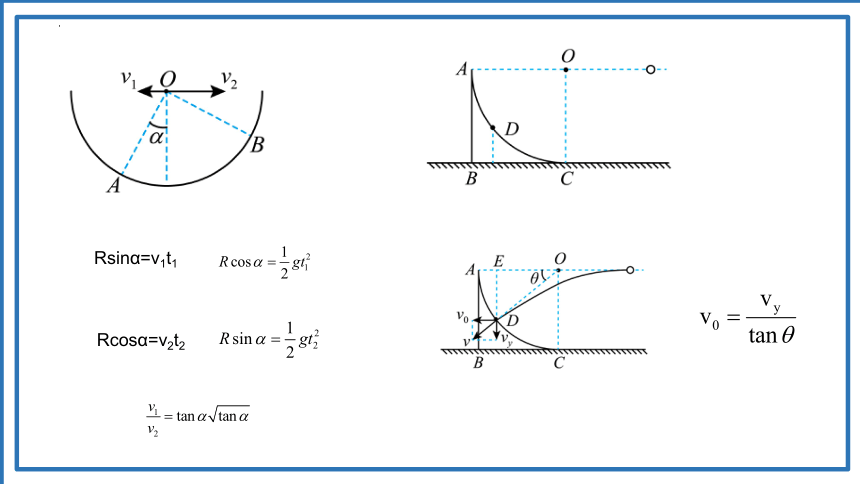
Rsinα=v1t1
Rcosα=v2t2
Part 02
典例
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
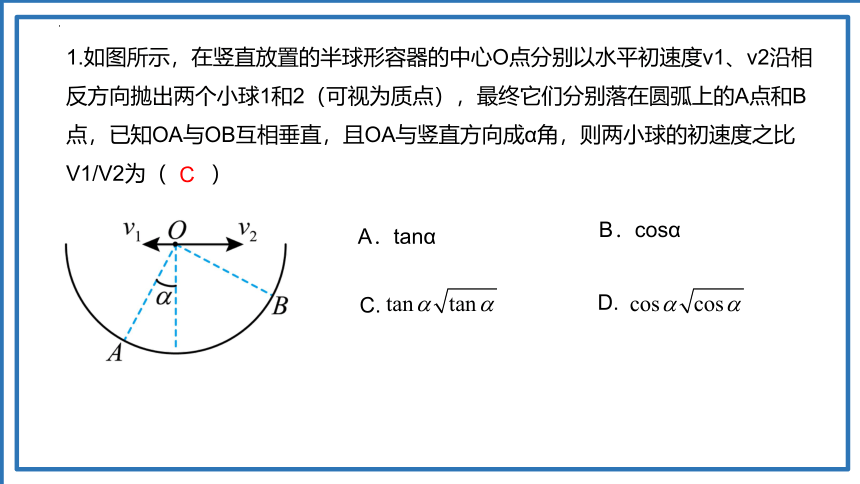
1.如图所示,在竖直放置的半球形容器的中心O点分别以水平初速度v1、v2沿相反方向抛出两个小球1和2(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球的初速度之比V1/V2为( )
A.tanα
B.cosα
C.
D.
C
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
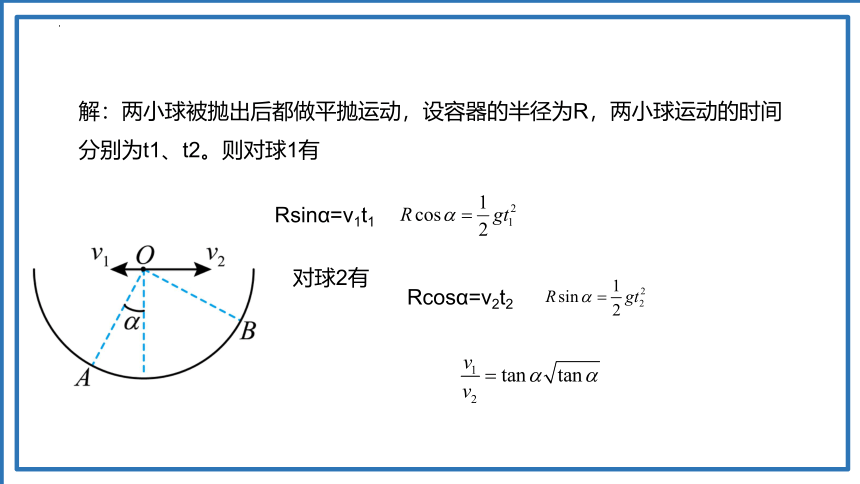
解:两小球被抛出后都做平抛运动,设容器的半径为R,两小球运动的时间分别为t1、t2。则对球1有
Rsinα=v1t1
对球2有
Rcosα=v2t2
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
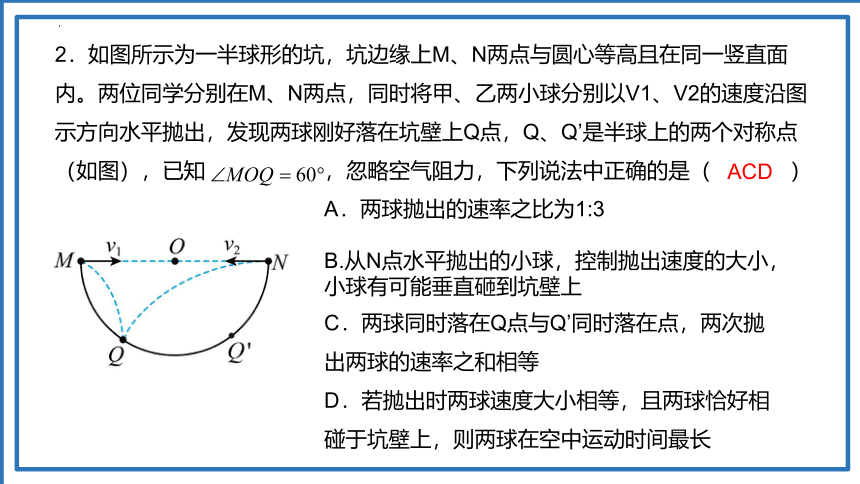
2.如图所示为一半球形的坑,坑边缘上M、N两点与圆心等高且在同一竖直面内。两位同学分别在M、N两点,同时将甲、乙两小球分别以V1、V2的速度沿图示方向水平抛出,发现两球刚好落在坑壁上Q点,Q、Q’是半球上的两个对称点(如图),已知 ,忽略空气阻力,下列说法中正确的是( )
A.两球抛出的速率之比为1:3
B.从N点水平抛出的小球,控制抛出速度的大小,小球有可能垂直砸到坑壁上
C.两球同时落在Q点与Q’同时落在点,两次抛出两球的速率之和相等
D.若抛出时两球速度大小相等,且两球恰好相碰于坑壁上,则两球在空中运动时间最长
ACD
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
3.如图所示,滑道ABC为四分之一圆弧,半径为2m,O为其圆心,C为圆弧最低点,与地面相切,在和O点等高的某位置水平抛出一个小球,垂直击中圆弧上的B点。弧AB的长度是弧BC的长度的2倍。忽略空气阻力,g取10m/s2,则抛出点与O点水平距离是( )
A.1m
B.2m
C.
D.
A
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
垂直击中圆弧上的B点,速度反向延长线过圆心,由弧AB的长度是弧BC的长度的2倍,可得
小球在竖直方向做自由落体运动,则竖直分速度
水平方向上的分速度可得
小球由抛出点运动到D点所用的时间为
则抛出点与O点水平距离
Part 03
随堂检测
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
1.如图所示, 是半圆弧的一条水平直径,O是圆弧的圆心,C是圆弧上一点,
,在A、O两点分别以一定的初速度V1、V2水平抛出两个小球,结果都落在 C点,则两个球抛出的初速度、的大小之比为( )
A.
C.
D.
B.
B
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
两球下落的高度相同,根据 知,下落的时间相同,设圆弧的半径为R,根据几何关系可得
则A点抛出的球平抛运动的水平位移
从O点抛出的球做平抛运动的水平位移为
根据 知
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
2.如图所示,一竖直圆弧形槽固定于水平地面上,O为圆心,AB为沿水平方向的直径。若在A点以初速度v1平抛一小球,小球将击中槽壁上的最低点D点;若A点小球抛出的同时,在C点以初速度v2向左平抛另一个小球并也能击中D点,已知∠COD=60°,且不计空气阻力,则( )
A.两小球同时落到D点
B.两小球初速度大小之比为
C.两小球落到D点时的速度方向与OD线夹角相等
D.两小球落到D点时的瞬时速率之比为
BD
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
A.根据
可知,向左平抛的另一个小球竖直下降的高度小一些,其先落到D点,
B.对A点抛出的小球有
对C点抛出的小球有
C.A点抛出的小球落到D点时
C点抛出的小球落到D点时
可知,两小球落到D点时的速度方向与OD线夹角不相等,C错误;
D.A点抛出的小球落到D点时
C点抛出的小球落到D点时
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
3.如图所示,半径为5m的四分之一圆弧ABC固定在水平地面上,O为圆心。在圆心O右侧同一水平线上某点处,水平向左抛出一个小球,小球可视为质点,恰好垂直击中圆弧上的D点,D点到水平地面的高度为2m,g取10 m/s2,则小球的抛出速度是( )
A.
B.
C.
D.
C
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
小球在竖直方向做自由落体运动,则竖直分速度
垂直击中D点,速度反向延长线过圆心,如下图所示
sin θ=
θ=37°
则在D点,分解速度可得
v0=
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
7.如图所示,同一竖直平面内有四分之一圆环 和倾角为53度的斜面 ,A 、 B两点与圆环BC的圆心O 等高。现将甲、乙小球分别从 、 两点以初速度 V1、V2 沿水平方向同时抛出,两球恰好在C 点相碰(不计空气阻力),已知 ,
下列说法正确的是( )
A.初速度V1 、V2 大小之比为3:4
B.若仅增大 V1 ,则两球不再相碰
C.若 V1 大小变为原来的一半,则甲球恰能落在斜面的中点D
D.若只抛出甲球并适当改变 V1 大小,则甲球可能垂直击中圆环BC
AD
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
A.甲、乙两球从等高处做平抛运动恰好在 点相碰,则时间相等,水平方向有
B.两球在竖直方向做自由落体运动,同一时间位于同一高度,若仅增大 ,两球会相碰,B错误;
C.若 大小变为原来的一半,在时间不变的情况下水平位移会变为原来的一半,但由于甲球会碰到斜面,下落高度减小,时间减小,所以甲球的水平位移小于原来的一半,不会落在斜面的中点,C错误;
D.若甲球垂直击中圆环BC ,则在落点速度的反向延长线过圆心 O,由推论知落点与 O点的水平距离
符合实际,因此只抛出甲球并适当改变 大小,则甲球可能垂直击中圆环 ,D正确。
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
如图所示,一个半径R=0.75m的半圆柱体放下水平地面上,一小球从圆柱体左端A点正上方的B点水平抛出(小球可视为质点),恰好从C点切线方向进入,已知O为半圆柱体圆心,OC与水平方向夹角为53°,重力加速度为g,则( )
A.小球从B点运动到C点所用时间为0.3s
B.小球从B点运动到C点所用时间为0.5s
C.小球做平抛运动的初速度为4m/s
D.小球做平抛运动的初速度为6m/s
AC
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
小球做平抛运动,飞行过程中恰好与半圆轨道相切于 C点,由几何关系知速度与水平方向的夹角为37度,设位移与水平方向的夹角为 ,则有
感谢各位老师的观看
THANKS
第五章 抛体运动
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
复习导入
平抛
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
x=v0tcos?
vx=v0cos?
vy=v0sin? - gt
Part 01
平抛与圆相结合
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
Rsinα=v1t1
Rcosα=v2t2
Part 02
典例
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
1.如图所示,在竖直放置的半球形容器的中心O点分别以水平初速度v1、v2沿相反方向抛出两个小球1和2(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,则两小球的初速度之比V1/V2为( )
A.tanα
B.cosα
C.
D.
C
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
解:两小球被抛出后都做平抛运动,设容器的半径为R,两小球运动的时间分别为t1、t2。则对球1有
Rsinα=v1t1
对球2有
Rcosα=v2t2
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
2.如图所示为一半球形的坑,坑边缘上M、N两点与圆心等高且在同一竖直面内。两位同学分别在M、N两点,同时将甲、乙两小球分别以V1、V2的速度沿图示方向水平抛出,发现两球刚好落在坑壁上Q点,Q、Q’是半球上的两个对称点(如图),已知 ,忽略空气阻力,下列说法中正确的是( )
A.两球抛出的速率之比为1:3
B.从N点水平抛出的小球,控制抛出速度的大小,小球有可能垂直砸到坑壁上
C.两球同时落在Q点与Q’同时落在点,两次抛出两球的速率之和相等
D.若抛出时两球速度大小相等,且两球恰好相碰于坑壁上,则两球在空中运动时间最长
ACD
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
3.如图所示,滑道ABC为四分之一圆弧,半径为2m,O为其圆心,C为圆弧最低点,与地面相切,在和O点等高的某位置水平抛出一个小球,垂直击中圆弧上的B点。弧AB的长度是弧BC的长度的2倍。忽略空气阻力,g取10m/s2,则抛出点与O点水平距离是( )
A.1m
B.2m
C.
D.
A
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
垂直击中圆弧上的B点,速度反向延长线过圆心,由弧AB的长度是弧BC的长度的2倍,可得
小球在竖直方向做自由落体运动,则竖直分速度
水平方向上的分速度可得
小球由抛出点运动到D点所用的时间为
则抛出点与O点水平距离
Part 03
随堂检测
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
1.如图所示, 是半圆弧的一条水平直径,O是圆弧的圆心,C是圆弧上一点,
,在A、O两点分别以一定的初速度V1、V2水平抛出两个小球,结果都落在 C点,则两个球抛出的初速度、的大小之比为( )
A.
C.
D.
B.
B
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
两球下落的高度相同,根据 知,下落的时间相同,设圆弧的半径为R,根据几何关系可得
则A点抛出的球平抛运动的水平位移
从O点抛出的球做平抛运动的水平位移为
根据 知
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
2.如图所示,一竖直圆弧形槽固定于水平地面上,O为圆心,AB为沿水平方向的直径。若在A点以初速度v1平抛一小球,小球将击中槽壁上的最低点D点;若A点小球抛出的同时,在C点以初速度v2向左平抛另一个小球并也能击中D点,已知∠COD=60°,且不计空气阻力,则( )
A.两小球同时落到D点
B.两小球初速度大小之比为
C.两小球落到D点时的速度方向与OD线夹角相等
D.两小球落到D点时的瞬时速率之比为
BD
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
A.根据
可知,向左平抛的另一个小球竖直下降的高度小一些,其先落到D点,
B.对A点抛出的小球有
对C点抛出的小球有
C.A点抛出的小球落到D点时
C点抛出的小球落到D点时
可知,两小球落到D点时的速度方向与OD线夹角不相等,C错误;
D.A点抛出的小球落到D点时
C点抛出的小球落到D点时
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
3.如图所示,半径为5m的四分之一圆弧ABC固定在水平地面上,O为圆心。在圆心O右侧同一水平线上某点处,水平向左抛出一个小球,小球可视为质点,恰好垂直击中圆弧上的D点,D点到水平地面的高度为2m,g取10 m/s2,则小球的抛出速度是( )
A.
B.
C.
D.
C
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
小球在竖直方向做自由落体运动,则竖直分速度
垂直击中D点,速度反向延长线过圆心,如下图所示
sin θ=
θ=37°
则在D点,分解速度可得
v0=
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
7.如图所示,同一竖直平面内有四分之一圆环 和倾角为53度的斜面 ,A 、 B两点与圆环BC的圆心O 等高。现将甲、乙小球分别从 、 两点以初速度 V1、V2 沿水平方向同时抛出,两球恰好在C 点相碰(不计空气阻力),已知 ,
下列说法正确的是( )
A.初速度V1 、V2 大小之比为3:4
B.若仅增大 V1 ,则两球不再相碰
C.若 V1 大小变为原来的一半,则甲球恰能落在斜面的中点D
D.若只抛出甲球并适当改变 V1 大小,则甲球可能垂直击中圆环BC
AD
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
A.甲、乙两球从等高处做平抛运动恰好在 点相碰,则时间相等,水平方向有
B.两球在竖直方向做自由落体运动,同一时间位于同一高度,若仅增大 ,两球会相碰,B错误;
C.若 大小变为原来的一半,在时间不变的情况下水平位移会变为原来的一半,但由于甲球会碰到斜面,下落高度减小,时间减小,所以甲球的水平位移小于原来的一半,不会落在斜面的中点,C错误;
D.若甲球垂直击中圆环BC ,则在落点速度的反向延长线过圆心 O,由推论知落点与 O点的水平距离
符合实际,因此只抛出甲球并适当改变 大小,则甲球可能垂直击中圆环 ,D正确。
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
如图所示,一个半径R=0.75m的半圆柱体放下水平地面上,一小球从圆柱体左端A点正上方的B点水平抛出(小球可视为质点),恰好从C点切线方向进入,已知O为半圆柱体圆心,OC与水平方向夹角为53°,重力加速度为g,则( )
A.小球从B点运动到C点所用时间为0.3s
B.小球从B点运动到C点所用时间为0.5s
C.小球做平抛运动的初速度为4m/s
D.小球做平抛运动的初速度为6m/s
AC
首先要突出说明的是选题的现实价值,每一个研究的目的都是为了指导现实生活,一定要讲清本选题的研究有什么实际作用、解决什么问题;其次再写课题的理论和学术价值。
小球做平抛运动,飞行过程中恰好与半圆轨道相切于 C点,由几何关系知速度与水平方向的夹角为37度,设位移与水平方向的夹角为 ,则有
感谢各位老师的观看
THANKS
