2022-2023学年北师大版九年级数学下册2.2 二次函数的图象与性质 同步练习题(含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学下册2.2 二次函数的图象与性质 同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 146.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 05:41:38 | ||
图片预览



文档简介
《2.2 二次函数的图象与性质》同步练习题
一.选择题(共31小题)
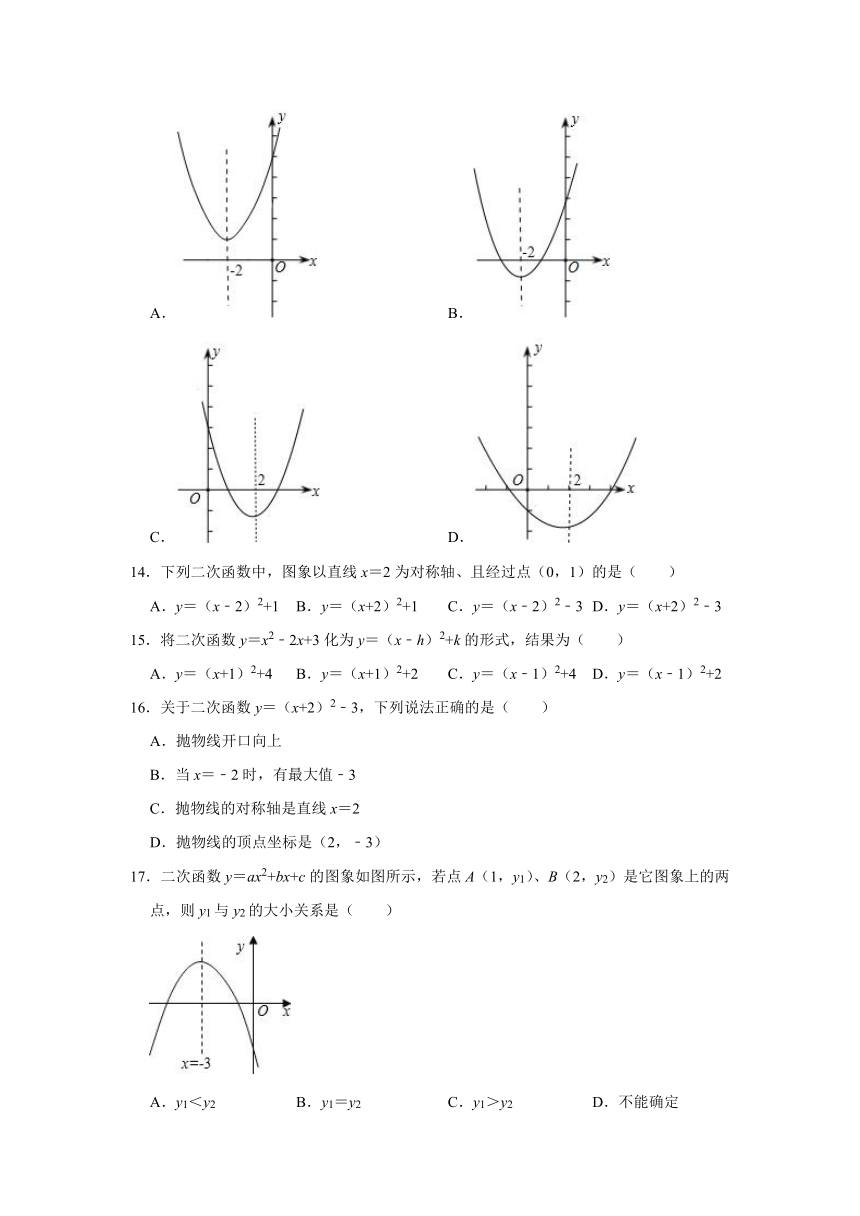
1.把二次函数y=﹣x2的图象先向右平移1个单位,再向上平移2个单位后得到一个新图象,则新图象所表示的二次函数的解析式是( )
A.y=﹣(x﹣1)2+2 B.y=﹣(x+1)2+2
C.y=﹣(x﹣1)2﹣2 D.y=﹣(x+1)2﹣2
2.二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
3.如图为二次函数y=ax2+bx+c的图象,给出下列说法:
①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,﹣1<x<3.
其中,正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:
①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=1.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤.
你认为其中正确信息的个数有( )
A.2个 B.3个 C.4个 D.5个
6.关于二次函数y=(x﹣3)2+5,下列说法中不正确的是( )
A.它的开口方向是向上
B.它的对称轴是直线x=3
C.它的顶点坐标(3,5)
D.当x<3时,y随x的增大而增大
7.直角坐标平面上将二次函数y=﹣2(x﹣1)2﹣2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )
A.(0,0) B.(1,﹣2) C.(0,﹣1) D.(﹣2,1)
8.若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是直线x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0)
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是( )
A.b2﹣4ac>0 B.a>0 C.c>0 D.
10.把抛物线y=2x2﹣3向右平移1个单位,再向上平移4个单位,则所得抛物线的解析式是( )
A.y=2(x+1)2+1 B.y=2(x﹣1)2+1
C.y=2(x+1)2﹣7 D.y=2(x﹣1)2﹣7
11.如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.你认为其中正确的有( )
A.4个 B.3个 C.2个 D.1个
12.如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
A.y=(x+1)2﹣1 B.y=(x+1)2+1 C.y=(x﹣1)2+1 D.y=(x﹣1)2﹣1
13.已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1,x2满足x1+x2=4和x1 x2=3,那么二次函数y=ax2+bx+c(a>0)的图象有可能是( )
A. B.
C. D.
14.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x﹣2)2+1 B.y=(x+2)2+1 C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
15.将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x+1)2+2 C.y=(x﹣1)2+4 D.y=(x﹣1)2+2
16.关于二次函数y=(x+2)2﹣3,下列说法正确的是( )
A.抛物线开口向上
B.当x=﹣2时,有最大值﹣3
C.抛物线的对称轴是直线x=2
D.抛物线的顶点坐标是(2,﹣3)
17.二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
18.把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式( )
A.y=﹣(x﹣2)2+2 B.y=(x﹣2)2+4
C.y=﹣(x+2)2+4 D.y=2+3
19.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>0;③b2﹣4ac>0;④a﹣b+c<0,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
20.在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位,所得图象的解析式为( )
A.y=2x2﹣2 B.y=2x2+2 C.y=2(x﹣2)2 D.y=2(x+2)2
21.关于x的二次函数y=﹣(x﹣1)2+2,下列说法正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(﹣1,2)
C.当x>1时,y随x的增大而减小
D.图象与y轴的交点坐标为(0,2)
22.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是( )
A.③④ B.②③ C.①④ D.①②③
23.把一个小球从地面竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:h=20t﹣5t2,则小球从抛出到落地的运动时间为( )
A. B.4s C.2s D.
24.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a+b+c>0
(2)方程ax2+bx+c=0两根之和大于零
(3)y随x的增大而增大
(4)一次函数y=x+bc的图象一定不过第二象限,
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
25.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
26.把抛物线y=x2向右平移2个单位,再向上平移1个单位,所得的抛物线的解析式为( )
A.y=(x﹣2)2+1 B.y=(x﹣2)2﹣1
C.y=(x+2)2+1 D.y=(x+1)2﹣2
27.下列图形中,阴影部分面积为1的是( )
A. B.
C. D.
28.在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A. B.
C. D.
29.抛物线y=﹣(x﹣3)2﹣5的对称轴是直线( )
A.x=﹣3 B.x=3 C.x=5 D.x=﹣5
30.抛物线y=x2﹣6x+21的顶点坐标是( )
A.(﹣6,﹣3) B.(﹣6,3) C.(6,3) D.(6,﹣3)
31.抛物线y=2(x+1)2﹣3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
二.填空题(共4小题)
32.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(,0),对称轴为直线x=﹣1,下列5个结论:①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b),其中正确的结论为 .(注:只填写正确结论的序号)
33.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc<0;②b>a+c;③2a﹣b=0;④b2﹣4ac<0.其中正确的结论有 个.
34.已知二次函数y=x2+bx+3的图象的顶点的横坐标是1,则b= .
35.已知某二次函数的图象具有下列特征:①开口方向向下,②以y轴为对称轴,③图象与x轴没有交点.试写出满足以上条件的一个二次函数的解析式(任写一个符合条件的即可) .
《2.2 二次函数的图象与性质》同步练习题
参考答案与试题解析
一.选择题(共31小题)
1.【解答】解:原抛物线的顶点为(0,0),先向右平移1个单位,再向上平移2个单位那么新抛物线的顶点为(1,2).
可设新抛物线的解析式为y=﹣(x﹣h)2+k代入2得:y=﹣(x﹣1)2+2.
故选:A.
2.【解答】解:二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标为(1,3).
故选:A.
3.【解答】解:∵抛物线的开口向上,
∴a>0,
∵对称轴在x的正半轴上,且是x=1,
∴﹣>0,
∴b<0,
∴ab<0,∴①正确;
∵根据图象可知:抛物线和x轴的交点坐标是(﹣1,0),(3,0),
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,∴②正确;
把x=1代入y=ax2+bx+c得:y=a+b+c<0,∴③错误;
∵根据图象可知:当x>1时,y随x值的增大而增大,∴④正确;
∵当y<0时,﹣1<x<3,∴⑤错误;
正确的有3个,
故选:C.
4.【解答】解:∵当y1=y2时,即﹣x2+4x=2x时,
解得:x=0或x=2,
∴当x>2时,利用函数图象可以得出y2>y1;当0<x<2时,y1>y2;当x<0时,利用函数图象可以得出y2>y1;
∴①错误;
∵抛物线y1=﹣x2+4x,直线y2=2x,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;
∴②正确;
∵抛物线y1=﹣x2+4x的最大值为4,故M大于4的x值不存在,
∴③正确;
∵如图:当0<x<2时,y1>y2;
当M=2,2x=2,x=1;
x>2时,y2>y1;
当M=2,﹣x2+4x=2,x1=2+,x2=2﹣(舍去),
∴使得M=2的x值是1或2+,
∴④错误;
∴正确的有②③两个.
故选:B.
5.【解答】解:①如图,∵抛物线开口方向向下,∴a<0.
∵对称轴x=﹣=﹣,∴b=a<0,
∴ab>0.故①正确;
②如图,当x=1时,y<0,即a+b+c<0.
故②正确;
③如图,当x=﹣1时,y=a﹣b+c>0,
∴2a﹣2b+2c>0,即3b﹣2b+2c>0,
∴b+2c>0.
故③正确;
④如图,当x=﹣时,y>0,即a﹣b+c>0.
∴a﹣2b+4c>0,
故④正确;
⑤如图,对称轴x=﹣=﹣,则.故⑤正确.
综上所述,正确的结论是①②③④⑤,共5个.
故选:D.
6.【解答】解:A、由抛物线可看出a=1>0,故开口向上,故此选项不符合题意;
B、抛物线的对称轴是直线x=3,故此选项不符合题意;
C、它的顶点坐标(3,5),故此选项不符合题意;
D、当x<3时,y随x的增大而减小,故此选项符合题意.
故选:D.
7.【解答】解:由题意得原抛物线的顶点为(1,﹣2),
∵图象向左平移1个单位,再向上平移1个单位,
∴新抛物线的顶点为(0,﹣1).
故选:C.
8.【解答】解:∵抛物线过点(0,﹣3),
∴抛物线的解析式为:y=x2﹣2x﹣3.
A、抛物线的二次项系数为1>0,抛物线的开口向上,正确.
B、根据抛物线的对称轴x=﹣=﹣=1,正确.
C、由A知抛物线的开口向上,二次函数有最小值,当x=1时,y的最小值为﹣4,而不是最大值.故本选项错误.
D、当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0),(3,0).正确.
故选:C.
9.【解答】解:A、正确,∵抛物线与x轴有两个交点,∴Δ=b2﹣4ac>0;
B、正确,∵抛物线开口向上,∴a>0;
C、正确,∵抛物线与y轴的交点在y轴的正半轴,∴c>0;
D、错误,∵抛物线的对称轴在y轴的右侧,∴﹣>0.
故选:D.
10.【解答】解:抛物线y=2x2﹣3的顶点坐标为(0,﹣3),
∵向右平移1个单位,向上平移4个单位,
∴平移后的抛物线顶点坐标为(1,1),
∴所得抛物线的解析式是y=2(x﹣1)2+1.
故选:B.
11.【解答】解:∵抛物线过点(1,0),
∴a+b+c=0,所以①正确;
∵抛物线的对称轴为直线x=﹣=﹣1,
∴2a﹣b=0,所以②错误;
∵点(1,0)关于直线x=﹣1的对称点为(﹣3,0),
∴抛物线与x轴两交点坐标为(﹣3,0),(1,0),
∴ax2+bx+c=0的两根分别为﹣3和1,所以③正确;
∵b=2a,a+b+c=0,
∴a+2a+c=0,即c=﹣3a,
∴a﹣2b+c=a﹣4a﹣3a=﹣6a,
∵抛物线开口向上,
∴a>0,
∴a﹣2b+c=﹣6a<0,所以④错误.
故选:C.
12.【解答】解:∵A在直线y=x上,
∴设A(m,m),
∵OA=,
∴m2+m2=()2,
解得:m=±1(m=﹣1舍去),
∴m=1,
∴A(1,1),
∴平移后的抛物线解析式为:y=(x﹣1)2+1,
故选:C.
13.【解答】解:∵已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1,x2满足x1+x2=4和x1 x2=3,
∴x1,x2是一元二次方程x2﹣4x+3=0的两个根,
∴(x﹣1)(x﹣3)=0,
解得:x1=1,x2=3
∴二次函数y=ax2+bx+c(a>0)与x轴的交点坐标为(1,0)和(3,0)
故选:C.
14.【解答】解:∵抛物线对称轴为直线x=2,
∴可排除B、D选项,
将点(0,1)代入A中,得(x﹣2)2+1=(0﹣2)2+1=5,故A选项错误,
代入C中,得(x﹣2)2﹣3=(0﹣2)2﹣3=1,故C选项正确.
故选:C.
15.【解答】解:y=x2﹣2x+3,
=(x2﹣2x+1)+2,
=(x﹣1)2+2.
故选:D.
16.【解答】解:A,由抛物线可看出a=1>0,故开口向上,正确;
B,由于开口方向向上,y有最小值,且在顶点,即x=﹣2时,y有最小值﹣3,错误;
C,抛物线的对称轴是直线x=﹣2,错误;
D,抛物线的顶点坐标是(﹣2,﹣3),错误.
故选:A.
17.【解答】解:从题中给出的图象可以看出,对称轴为直线x=﹣3,a<0,
又点A、B位于对称轴右侧,y随x的增大而减小,
则y1>y2.
故选:C.
18.【解答】解:y=﹣x2﹣x+3=﹣(x2+4x+4)+1+3=﹣(x+2)2+4
故选:C.
19.【解答】解:①∵抛物线开口向下,∴a<0,而对称轴在y轴左侧,∴a、b同号,即b<0,正确;
②∵抛物线与y轴的交点在正半轴,∴c>0,正确;
③∵图象与x轴有两个交点,∴b2﹣4ac>0,正确;
④∵由图象可知当x=﹣1时,对应的函数值y=a﹣b+c>0,错误.
故选:C.
20.【解答】解:二次函数y=2x2的图象向上平移2个单位,得y=2x2+2.
故选:B.
21.【解答】解:∵这个函数的顶点是(1,2),
∴函数的开口向下,对称轴是直线x=1,
∴在对称轴的左侧y随x的增大而增大,在对称轴的右侧y随x的增大而减小.
故选:C.
22.【解答】解:①当x=1时,y=a+b+c=0,故①错误;
②当x=﹣1时,图象与x轴交点负半轴明显大于﹣1,
∴y=a﹣b+c<0,
故②正确;
③由抛物线的开口向下知a<0,
∵对称轴为0<x=﹣<1,
∴2a+b<0,
故③正确;
④对称轴为x=﹣>0,a<0
∴a、b异号,即b>0,
由图知抛物线与y轴交于正半轴,∴c>0
∴abc<0,
故④错误;
∴正确结论的序号为②③.
故选:B.
23.【解答】解:根据题意得;h=0,
0=20t﹣5t2
t=4或t=0(舍去).
则小球从抛出到落地的运动时间为4s.
故选:B.
24.【解答】解:(1)利用图象可知,x=1时函数值在x轴上方,∴a+b+c>0,
故此选项正确;
(2)结合图象可知方程ax2+bx+c=0两根之和大于零,故此选项正确;
(3)y随x的增大而增大,根据二次函数增减性得出,对称轴两侧增减性不同,故此选项错误;
(4)一次函数y=x+bc的图象一定不过第二象限,结合图象可知b<0,c<0,
∴bc>0,
∴一次函数y=x+bc的图象一定不过第四象限,故此选项错误.
故选:C.
25.【解答】解:①∵图象与x轴有交点,对称轴为x==﹣1,与y轴的交点在y轴的正半轴上,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2﹣4ac>0,
即b2>4ac,故本选项正确,
②∵抛物线的开口向下,
∴a<0,
∵与y轴的交点在y轴的正半轴上,
∴c>0,
∵对称轴为x==﹣1,
∴2a=b,
∴2a+b=4a,a≠0,
故本选项错误,
③∵x=﹣1时y有最大值,
由图象可知y≠0,故本选项错误,
④把x=1,x=﹣3代入解析式得a+b+c=0,9a﹣3b+c=0,
两边相加整理得5a﹣b=﹣c<0,即5a<b,故本选项正确.
故选:B.
26.【解答】解:原抛物线的顶点为(0,0),向右平移2个单位,再向上平移1个单位,那么新抛物线的顶点为(2,1).可设新抛物线的解析式为y=(x﹣h)2+k,代入得y=(x﹣2)2+1.
故选:A.
27.【解答】解:A、S梯=1.5;
B、S△=;
C、S△=;
D、S阴影=1.
故选:D.
28.【解答】解:A、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b<0,正确;
B、由抛物线可知,a>0,由直线可知,a<0,错误;
C、由抛物线可知,a<0,x=﹣>0,得b>0,由直线可知,a<0,b<0,错误;
D、由抛物线可知,a<0,由直线可知,a>0,错误.
故选:A.
29.【解答】解:∵抛物线y=﹣(x﹣3)2﹣5是抛物线的顶点式,
根据顶点式的坐标特点,抛物线对称轴是直线x=3.
故选:B.
30.【解答】解:∵y=x2﹣6x+21=(x2﹣12x)+21=(x2﹣12x+36﹣36)+21=(x﹣6)2+3,
∴抛物线y=x2﹣6x+21的顶点坐标是(6,3).
故选:C.
31.【解答】解:∵y=2(x+1)2﹣3是抛物线的顶点式,
根据顶点式的坐标特点可知,顶点坐标为(﹣1,﹣3),
故选:D.
二.填空题(共4小题)
32.【解答】解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴为直线x=﹣=﹣1,
∴b=2a,则2a﹣b=0,所以③错误;
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵x=时,y=0,
∴a+b+c=0,即a+2b+4c=0,所以②正确;
∵a=b,a+b+c>0,
∴b+2b+c>0,即3b+2c>0,所以④正确;
∵x=﹣1时,函数值最小,
∴a﹣b+c<am2﹣mb+c(m≠1),
∴a﹣b≤m(am﹣b),所以⑤错误.
故答案为②④.
33.【解答】解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=﹣,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①正确;
根据图象知道当x=﹣1时,y=a﹣b+c<0,
∴a+c<b,故②正确;
∵对称轴x=1=﹣,∴2a=﹣b,
∴2a+b=0,故③错误;
根据图象知道抛物线与x轴有两个交点,
∴b2﹣4ac>0,故④错误.
正确的有2个,
故答案为:2.
34.【解答】解:∵二次函数图象的顶点横坐标为1,
∴对称轴x=﹣=1,
解得b=﹣2.
故答案为:﹣2.
35.【解答】解:∵二次函数的图象具有下列特征:①开口方向向下,②以y轴为对称轴,③图象与x轴没有交点,
∴满足以上条件的一个二次函数的解析式(任写一个符合条件的即可)为y=﹣x2﹣1.
故答案为:y=﹣x2﹣1.
一.选择题(共31小题)
1.把二次函数y=﹣x2的图象先向右平移1个单位,再向上平移2个单位后得到一个新图象,则新图象所表示的二次函数的解析式是( )
A.y=﹣(x﹣1)2+2 B.y=﹣(x+1)2+2
C.y=﹣(x﹣1)2﹣2 D.y=﹣(x+1)2﹣2
2.二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
3.如图为二次函数y=ax2+bx+c的图象,给出下列说法:
①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,﹣1<x<3.
其中,正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:
①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=1.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤.
你认为其中正确信息的个数有( )
A.2个 B.3个 C.4个 D.5个
6.关于二次函数y=(x﹣3)2+5,下列说法中不正确的是( )
A.它的开口方向是向上
B.它的对称轴是直线x=3
C.它的顶点坐标(3,5)
D.当x<3时,y随x的增大而增大
7.直角坐标平面上将二次函数y=﹣2(x﹣1)2﹣2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )
A.(0,0) B.(1,﹣2) C.(0,﹣1) D.(﹣2,1)
8.若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是直线x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0)
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是( )
A.b2﹣4ac>0 B.a>0 C.c>0 D.
10.把抛物线y=2x2﹣3向右平移1个单位,再向上平移4个单位,则所得抛物线的解析式是( )
A.y=2(x+1)2+1 B.y=2(x﹣1)2+1
C.y=2(x+1)2﹣7 D.y=2(x﹣1)2﹣7
11.如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.你认为其中正确的有( )
A.4个 B.3个 C.2个 D.1个
12.如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
A.y=(x+1)2﹣1 B.y=(x+1)2+1 C.y=(x﹣1)2+1 D.y=(x﹣1)2﹣1
13.已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1,x2满足x1+x2=4和x1 x2=3,那么二次函数y=ax2+bx+c(a>0)的图象有可能是( )
A. B.
C. D.
14.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x﹣2)2+1 B.y=(x+2)2+1 C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
15.将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x+1)2+2 C.y=(x﹣1)2+4 D.y=(x﹣1)2+2
16.关于二次函数y=(x+2)2﹣3,下列说法正确的是( )
A.抛物线开口向上
B.当x=﹣2时,有最大值﹣3
C.抛物线的对称轴是直线x=2
D.抛物线的顶点坐标是(2,﹣3)
17.二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
18.把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式( )
A.y=﹣(x﹣2)2+2 B.y=(x﹣2)2+4
C.y=﹣(x+2)2+4 D.y=2+3
19.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>0;③b2﹣4ac>0;④a﹣b+c<0,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
20.在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位,所得图象的解析式为( )
A.y=2x2﹣2 B.y=2x2+2 C.y=2(x﹣2)2 D.y=2(x+2)2
21.关于x的二次函数y=﹣(x﹣1)2+2,下列说法正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(﹣1,2)
C.当x>1时,y随x的增大而减小
D.图象与y轴的交点坐标为(0,2)
22.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是( )
A.③④ B.②③ C.①④ D.①②③
23.把一个小球从地面竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:h=20t﹣5t2,则小球从抛出到落地的运动时间为( )
A. B.4s C.2s D.
24.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a+b+c>0
(2)方程ax2+bx+c=0两根之和大于零
(3)y随x的增大而增大
(4)一次函数y=x+bc的图象一定不过第二象限,
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
25.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
26.把抛物线y=x2向右平移2个单位,再向上平移1个单位,所得的抛物线的解析式为( )
A.y=(x﹣2)2+1 B.y=(x﹣2)2﹣1
C.y=(x+2)2+1 D.y=(x+1)2﹣2
27.下列图形中,阴影部分面积为1的是( )
A. B.
C. D.
28.在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A. B.
C. D.
29.抛物线y=﹣(x﹣3)2﹣5的对称轴是直线( )
A.x=﹣3 B.x=3 C.x=5 D.x=﹣5
30.抛物线y=x2﹣6x+21的顶点坐标是( )
A.(﹣6,﹣3) B.(﹣6,3) C.(6,3) D.(6,﹣3)
31.抛物线y=2(x+1)2﹣3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(1,﹣3) D.(﹣1,﹣3)
二.填空题(共4小题)
32.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(,0),对称轴为直线x=﹣1,下列5个结论:①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b),其中正确的结论为 .(注:只填写正确结论的序号)
33.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc<0;②b>a+c;③2a﹣b=0;④b2﹣4ac<0.其中正确的结论有 个.
34.已知二次函数y=x2+bx+3的图象的顶点的横坐标是1,则b= .
35.已知某二次函数的图象具有下列特征:①开口方向向下,②以y轴为对称轴,③图象与x轴没有交点.试写出满足以上条件的一个二次函数的解析式(任写一个符合条件的即可) .
《2.2 二次函数的图象与性质》同步练习题
参考答案与试题解析
一.选择题(共31小题)
1.【解答】解:原抛物线的顶点为(0,0),先向右平移1个单位,再向上平移2个单位那么新抛物线的顶点为(1,2).
可设新抛物线的解析式为y=﹣(x﹣h)2+k代入2得:y=﹣(x﹣1)2+2.
故选:A.
2.【解答】解:二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标为(1,3).
故选:A.
3.【解答】解:∵抛物线的开口向上,
∴a>0,
∵对称轴在x的正半轴上,且是x=1,
∴﹣>0,
∴b<0,
∴ab<0,∴①正确;
∵根据图象可知:抛物线和x轴的交点坐标是(﹣1,0),(3,0),
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,∴②正确;
把x=1代入y=ax2+bx+c得:y=a+b+c<0,∴③错误;
∵根据图象可知:当x>1时,y随x值的增大而增大,∴④正确;
∵当y<0时,﹣1<x<3,∴⑤错误;
正确的有3个,
故选:C.
4.【解答】解:∵当y1=y2时,即﹣x2+4x=2x时,
解得:x=0或x=2,
∴当x>2时,利用函数图象可以得出y2>y1;当0<x<2时,y1>y2;当x<0时,利用函数图象可以得出y2>y1;
∴①错误;
∵抛物线y1=﹣x2+4x,直线y2=2x,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;
∴②正确;
∵抛物线y1=﹣x2+4x的最大值为4,故M大于4的x值不存在,
∴③正确;
∵如图:当0<x<2时,y1>y2;
当M=2,2x=2,x=1;
x>2时,y2>y1;
当M=2,﹣x2+4x=2,x1=2+,x2=2﹣(舍去),
∴使得M=2的x值是1或2+,
∴④错误;
∴正确的有②③两个.
故选:B.
5.【解答】解:①如图,∵抛物线开口方向向下,∴a<0.
∵对称轴x=﹣=﹣,∴b=a<0,
∴ab>0.故①正确;
②如图,当x=1时,y<0,即a+b+c<0.
故②正确;
③如图,当x=﹣1时,y=a﹣b+c>0,
∴2a﹣2b+2c>0,即3b﹣2b+2c>0,
∴b+2c>0.
故③正确;
④如图,当x=﹣时,y>0,即a﹣b+c>0.
∴a﹣2b+4c>0,
故④正确;
⑤如图,对称轴x=﹣=﹣,则.故⑤正确.
综上所述,正确的结论是①②③④⑤,共5个.
故选:D.
6.【解答】解:A、由抛物线可看出a=1>0,故开口向上,故此选项不符合题意;
B、抛物线的对称轴是直线x=3,故此选项不符合题意;
C、它的顶点坐标(3,5),故此选项不符合题意;
D、当x<3时,y随x的增大而减小,故此选项符合题意.
故选:D.
7.【解答】解:由题意得原抛物线的顶点为(1,﹣2),
∵图象向左平移1个单位,再向上平移1个单位,
∴新抛物线的顶点为(0,﹣1).
故选:C.
8.【解答】解:∵抛物线过点(0,﹣3),
∴抛物线的解析式为:y=x2﹣2x﹣3.
A、抛物线的二次项系数为1>0,抛物线的开口向上,正确.
B、根据抛物线的对称轴x=﹣=﹣=1,正确.
C、由A知抛物线的开口向上,二次函数有最小值,当x=1时,y的最小值为﹣4,而不是最大值.故本选项错误.
D、当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0),(3,0).正确.
故选:C.
9.【解答】解:A、正确,∵抛物线与x轴有两个交点,∴Δ=b2﹣4ac>0;
B、正确,∵抛物线开口向上,∴a>0;
C、正确,∵抛物线与y轴的交点在y轴的正半轴,∴c>0;
D、错误,∵抛物线的对称轴在y轴的右侧,∴﹣>0.
故选:D.
10.【解答】解:抛物线y=2x2﹣3的顶点坐标为(0,﹣3),
∵向右平移1个单位,向上平移4个单位,
∴平移后的抛物线顶点坐标为(1,1),
∴所得抛物线的解析式是y=2(x﹣1)2+1.
故选:B.
11.【解答】解:∵抛物线过点(1,0),
∴a+b+c=0,所以①正确;
∵抛物线的对称轴为直线x=﹣=﹣1,
∴2a﹣b=0,所以②错误;
∵点(1,0)关于直线x=﹣1的对称点为(﹣3,0),
∴抛物线与x轴两交点坐标为(﹣3,0),(1,0),
∴ax2+bx+c=0的两根分别为﹣3和1,所以③正确;
∵b=2a,a+b+c=0,
∴a+2a+c=0,即c=﹣3a,
∴a﹣2b+c=a﹣4a﹣3a=﹣6a,
∵抛物线开口向上,
∴a>0,
∴a﹣2b+c=﹣6a<0,所以④错误.
故选:C.
12.【解答】解:∵A在直线y=x上,
∴设A(m,m),
∵OA=,
∴m2+m2=()2,
解得:m=±1(m=﹣1舍去),
∴m=1,
∴A(1,1),
∴平移后的抛物线解析式为:y=(x﹣1)2+1,
故选:C.
13.【解答】解:∵已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1,x2满足x1+x2=4和x1 x2=3,
∴x1,x2是一元二次方程x2﹣4x+3=0的两个根,
∴(x﹣1)(x﹣3)=0,
解得:x1=1,x2=3
∴二次函数y=ax2+bx+c(a>0)与x轴的交点坐标为(1,0)和(3,0)
故选:C.
14.【解答】解:∵抛物线对称轴为直线x=2,
∴可排除B、D选项,
将点(0,1)代入A中,得(x﹣2)2+1=(0﹣2)2+1=5,故A选项错误,
代入C中,得(x﹣2)2﹣3=(0﹣2)2﹣3=1,故C选项正确.
故选:C.
15.【解答】解:y=x2﹣2x+3,
=(x2﹣2x+1)+2,
=(x﹣1)2+2.
故选:D.
16.【解答】解:A,由抛物线可看出a=1>0,故开口向上,正确;
B,由于开口方向向上,y有最小值,且在顶点,即x=﹣2时,y有最小值﹣3,错误;
C,抛物线的对称轴是直线x=﹣2,错误;
D,抛物线的顶点坐标是(﹣2,﹣3),错误.
故选:A.
17.【解答】解:从题中给出的图象可以看出,对称轴为直线x=﹣3,a<0,
又点A、B位于对称轴右侧,y随x的增大而减小,
则y1>y2.
故选:C.
18.【解答】解:y=﹣x2﹣x+3=﹣(x2+4x+4)+1+3=﹣(x+2)2+4
故选:C.
19.【解答】解:①∵抛物线开口向下,∴a<0,而对称轴在y轴左侧,∴a、b同号,即b<0,正确;
②∵抛物线与y轴的交点在正半轴,∴c>0,正确;
③∵图象与x轴有两个交点,∴b2﹣4ac>0,正确;
④∵由图象可知当x=﹣1时,对应的函数值y=a﹣b+c>0,错误.
故选:C.
20.【解答】解:二次函数y=2x2的图象向上平移2个单位,得y=2x2+2.
故选:B.
21.【解答】解:∵这个函数的顶点是(1,2),
∴函数的开口向下,对称轴是直线x=1,
∴在对称轴的左侧y随x的增大而增大,在对称轴的右侧y随x的增大而减小.
故选:C.
22.【解答】解:①当x=1时,y=a+b+c=0,故①错误;
②当x=﹣1时,图象与x轴交点负半轴明显大于﹣1,
∴y=a﹣b+c<0,
故②正确;
③由抛物线的开口向下知a<0,
∵对称轴为0<x=﹣<1,
∴2a+b<0,
故③正确;
④对称轴为x=﹣>0,a<0
∴a、b异号,即b>0,
由图知抛物线与y轴交于正半轴,∴c>0
∴abc<0,
故④错误;
∴正确结论的序号为②③.
故选:B.
23.【解答】解:根据题意得;h=0,
0=20t﹣5t2
t=4或t=0(舍去).
则小球从抛出到落地的运动时间为4s.
故选:B.
24.【解答】解:(1)利用图象可知,x=1时函数值在x轴上方,∴a+b+c>0,
故此选项正确;
(2)结合图象可知方程ax2+bx+c=0两根之和大于零,故此选项正确;
(3)y随x的增大而增大,根据二次函数增减性得出,对称轴两侧增减性不同,故此选项错误;
(4)一次函数y=x+bc的图象一定不过第二象限,结合图象可知b<0,c<0,
∴bc>0,
∴一次函数y=x+bc的图象一定不过第四象限,故此选项错误.
故选:C.
25.【解答】解:①∵图象与x轴有交点,对称轴为x==﹣1,与y轴的交点在y轴的正半轴上,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2﹣4ac>0,
即b2>4ac,故本选项正确,
②∵抛物线的开口向下,
∴a<0,
∵与y轴的交点在y轴的正半轴上,
∴c>0,
∵对称轴为x==﹣1,
∴2a=b,
∴2a+b=4a,a≠0,
故本选项错误,
③∵x=﹣1时y有最大值,
由图象可知y≠0,故本选项错误,
④把x=1,x=﹣3代入解析式得a+b+c=0,9a﹣3b+c=0,
两边相加整理得5a﹣b=﹣c<0,即5a<b,故本选项正确.
故选:B.
26.【解答】解:原抛物线的顶点为(0,0),向右平移2个单位,再向上平移1个单位,那么新抛物线的顶点为(2,1).可设新抛物线的解析式为y=(x﹣h)2+k,代入得y=(x﹣2)2+1.
故选:A.
27.【解答】解:A、S梯=1.5;
B、S△=;
C、S△=;
D、S阴影=1.
故选:D.
28.【解答】解:A、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b<0,正确;
B、由抛物线可知,a>0,由直线可知,a<0,错误;
C、由抛物线可知,a<0,x=﹣>0,得b>0,由直线可知,a<0,b<0,错误;
D、由抛物线可知,a<0,由直线可知,a>0,错误.
故选:A.
29.【解答】解:∵抛物线y=﹣(x﹣3)2﹣5是抛物线的顶点式,
根据顶点式的坐标特点,抛物线对称轴是直线x=3.
故选:B.
30.【解答】解:∵y=x2﹣6x+21=(x2﹣12x)+21=(x2﹣12x+36﹣36)+21=(x﹣6)2+3,
∴抛物线y=x2﹣6x+21的顶点坐标是(6,3).
故选:C.
31.【解答】解:∵y=2(x+1)2﹣3是抛物线的顶点式,
根据顶点式的坐标特点可知,顶点坐标为(﹣1,﹣3),
故选:D.
二.填空题(共4小题)
32.【解答】解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴为直线x=﹣=﹣1,
∴b=2a,则2a﹣b=0,所以③错误;
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵x=时,y=0,
∴a+b+c=0,即a+2b+4c=0,所以②正确;
∵a=b,a+b+c>0,
∴b+2b+c>0,即3b+2c>0,所以④正确;
∵x=﹣1时,函数值最小,
∴a﹣b+c<am2﹣mb+c(m≠1),
∴a﹣b≤m(am﹣b),所以⑤错误.
故答案为②④.
33.【解答】解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=﹣,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①正确;
根据图象知道当x=﹣1时,y=a﹣b+c<0,
∴a+c<b,故②正确;
∵对称轴x=1=﹣,∴2a=﹣b,
∴2a+b=0,故③错误;
根据图象知道抛物线与x轴有两个交点,
∴b2﹣4ac>0,故④错误.
正确的有2个,
故答案为:2.
34.【解答】解:∵二次函数图象的顶点横坐标为1,
∴对称轴x=﹣=1,
解得b=﹣2.
故答案为:﹣2.
35.【解答】解:∵二次函数的图象具有下列特征:①开口方向向下,②以y轴为对称轴,③图象与x轴没有交点,
∴满足以上条件的一个二次函数的解析式(任写一个符合条件的即可)为y=﹣x2﹣1.
故答案为:y=﹣x2﹣1.
