黑龙江省哈尔滨市南岗区2022-2023学年九年级上学期数学期末试卷(含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市南岗区2022-2023学年九年级上学期数学期末试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 20:15:09 | ||
图片预览



文档简介
2022-2023学年度上学期九年级
数学试卷
考生须知:
1. 本试卷满分为120分,考试时间为120分钟。
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内。
3. 请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。
4. 选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
5.保持卡面整洁,不要折叠、不要弄脏、不要弄皱,不准使用涂改液、修正带、刮纸刀。
第I卷 选择题(共30分)(涂卡)
一、选择题(每小题3分,共计30分)
1. 在实数-2,0,,2中,为负实数的是( )
A. -2 B.0 C. D.2
2.下列计算正确的是( )。
A. B.
C. D.
3.下列四种图形中,对称轴条数最多的是( )
A.等边三角形 B.长方形 C.正方形 D.圆
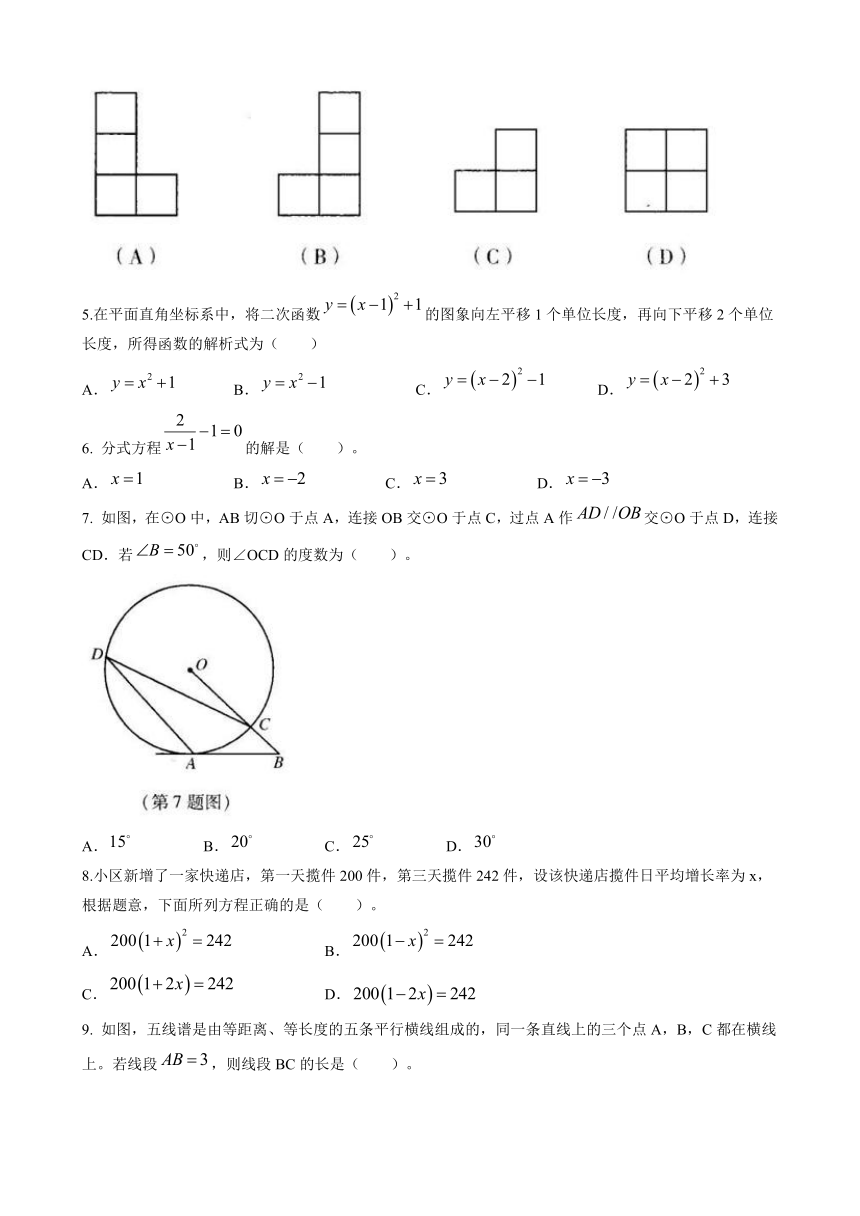
4. 如图所示的几何体是由5个完全相同的小正方体组成,它的主视图是( )
5.在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )
A. B. C. D.
6. 分式方程的解是( )。
A. B. C. D.
7. 如图,在⊙O中,AB切⊙O于点A,连接OB交⊙O于点C,过点A作交⊙O于点D,连接CD.若,则∠OCD的度数为( )。
A. B. C. D.
8.小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )。
A. B.
C. D.
9. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上。若线段,则线段BC的长是( )。
A. B.1 C. D.2
10.一辆汽车行驶30km后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶1h到达目的地。汽车行驶的时间x(单位:h)与行驶的路程y(单位:km)之间的关系如图所示。请结合图象,判断以下说法正确的是( )
A.汽车在高速路上行驶了2.5h
B.汽车在高速路上行驶的路程是180km
C.汽车在高速路上行驶的平均速度是72km/h
D.汽车在乡村道路上行驶的平均速度是40km/h
第II卷 非选择题(共90分)
二、填空题(每小题3分,共计30分)
11. 2022年5月14日,编号为B-001J的C919大飞机首飞成功。数据显示,C919大飞机的单价约为65300000元,数据65300000用科学记数法表示为___________。
12.在函数中,自变量x的取值范围是___________。
13. 计算的结果是___________。
14. 把多项式分解因式的结果是___________。
15. 不等式组的解集是___________。
16.若反比例函数的图象经过点(2,-3),则k的值为___________。
17. 在△ABC中,,点D在射线BA上,,连接CD,则∠BCD的大小是___________度。
18.一个不透明的口袋中,有2个红球和4个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个球,摸到红球的概率是___________。
19. 若扇形的弧长为π,半径为,则它的圆心角为___________度。
20.如图,在正方形ABCD中,点E在BC上,连接AE,过点E作交CD于点F,连接AF,,若,则线段EF的长为___________。
三、解答题(其中21-22题各7分,题各8分,题各10分,共计60分)
21.(本题7分)
先化简,再求代数式的值,其中。
22.(本题7分)
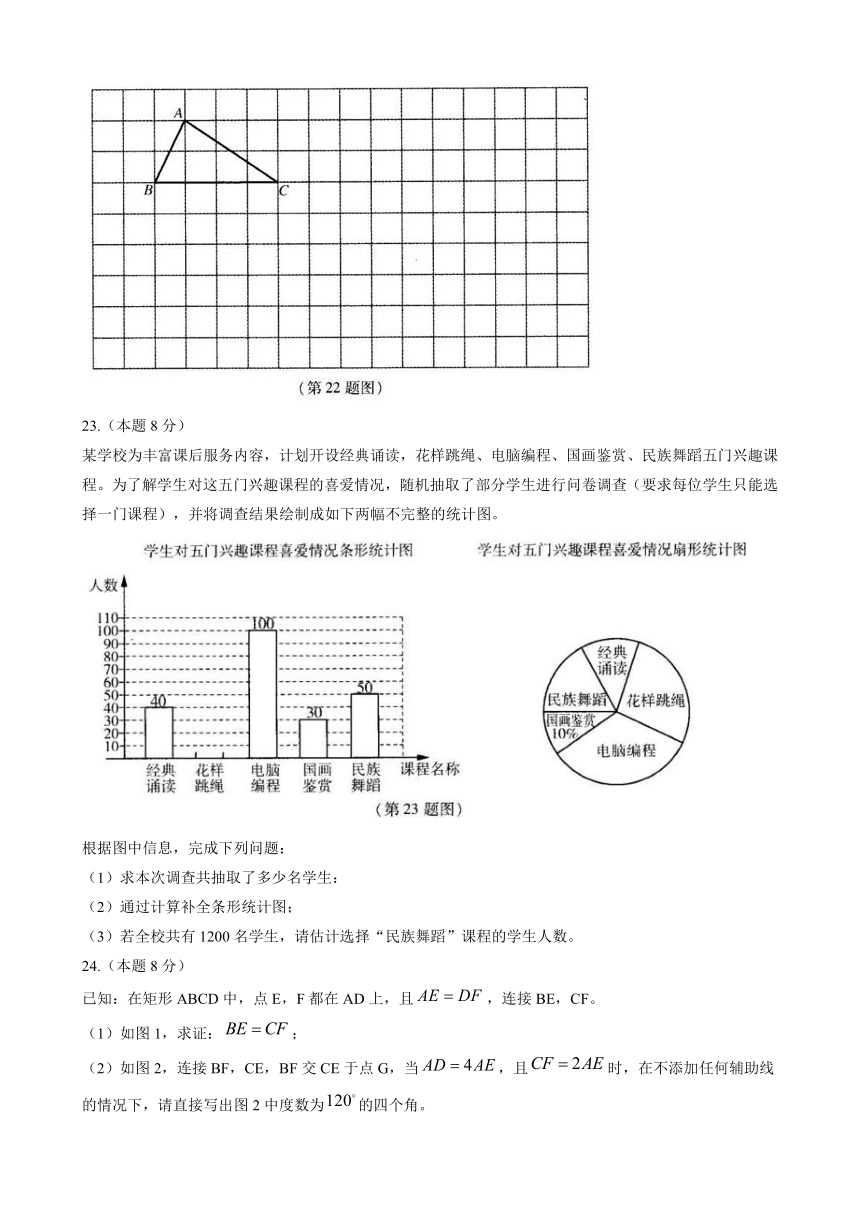
如图,在每个小正方形的边长为1个单位长度的网格中,△ABC的顶点均在格点(网格线的交点)上。
(1)将△ABC向右平移5个单位长度得到,画出;
(2)将(1)中的绕点逆时针旋转得到,画出△;
(3)连接,直接写出线段的长。
23.(本题8分)
某学校为丰富课后服务内容,计划开设经典诵读,花样跳绳、电脑编程、国画鉴赏、民族舞蹈五门兴趣课程。为了解学生对这五门兴趣课程的喜爱情况,随机抽取了部分学生进行问卷调查(要求每位学生只能选择一门课程),并将调查结果绘制成如下两幅不完整的统计图。
根据图中信息,完成下列问题:
(1)求本次调查共抽取了多少名学生:
(2)通过计算补全条形统计图;
(3)若全校共有1200名学生,请估计选择“民族舞蹈”课程的学生人数。
24.(本题8分)
已知:在矩形ABCD中,点E,F都在AD上,且,连接BE,CF。
(1)如图1,求证:;
(2)如图2,连接BF,CE,BF交CE于点G,当,且时,在不添加任何辅助线的情况下,请直接写出图2中度数为的四个角。
25.(本题10分)
某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球。已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元。
(1)求篮球和足球的单价分别是多少元;
(2)学校计划采购篮球、足球共50个,且总费用不超过5500元。那么最多采购篮球多少个?
26.(本题10分)
已知:四边形ABCD是⊙O的内接四边形,,连接AC。
(1)如图1,求证:;
(2)如图2,连接BD交AC于点E,点F在AC上,且,过点F作交CD于点G,求证:;
(3)如图3,在(2)的条件下,AC是⊙O的直径,点F在OC上,若求线段AB的长。
27.(本题10分)
已知:在平面直角坐标系中,点O是坐标原点,抛物线交x轴于点A(-3,0)和点B,交y轴于点C,连接AC,BC。
(1)如图1,求∠ACB的度数;
(2)如图2,直线交线段OB于点D,交y轴于点E,连接CD,设△CDE的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,线段CD绕点C逆时针旋转,得到线段CF,连接AF,取线段AF的中点G,连接BF,GC,分别延长BF,CC交于点H。点K在第二象限抛物线上,连接KE,当点K的横坐标为-2时,,求S的值。
2022-2023学年度上学期
九年级数学科参考答案及评分标准
一、选择题(每小题3分,共计30分)
1 2 3 4 5 6 7 8 9 10
A D D A B C B A C D
二、填空题(每小题3分,共计30分)
题号 11 12 13 14 15
答案 6.53×107 y(x-y)2 -3≤x<-1
题号 16 17 18 19 20
答案 -6 10或100 120
三、解答题(其中21-22题各7分,23-24题各8分,题各10分,共计60分)
21.(本题7分)
解:
原式。。。。。。。。。。。1分
。。。。。。2分
。。。。。。。。。。。。1分
∵。。。。。。。。。2分
∴原式。。
22.(本题7分)
解:(1)如图 正确画图。。。。3分
(2)如图 正确画图。。。。3分
(3)。。。。。。。1分
23.(本题8分)
解:(1)。。。。。2分
。。。。。。1分
答:本次调查共抽取了300名学生。
(2)。。。。。。。1分
正确补图。。。。。。1分
(3)。。。。。。2分
答:估计选择“民族舞蹈”课程的学生人数为200人。。。。。。。。。。。。。。1分
24.(本题8分)
(1)证明:如图1 ∵四边形ABCD为矩形 ∴。。。。。。。2分
又∵ ∴。。。。。。。。。1分
∴。。。。。。。。。
(2)如图2 ∠BEF,∠CFE,∠BGC,∠EGE。。
25.(本题10分)
(1)解:设篮球的单价为x元,足球的单价为y元。
根据题意 得。。。。。。。3分
解得。。。。。。。。。。2分
答:篮球的单价为120元,足球的单价为90元。
(2)设采购篮球m个,则采购足球)个。
根据题意 得。。。。。2分
解得。
∵m为整数 ∴m最大取33.。。。。。1分
答:最多采购篮球33个。。。。。。。1分
26.(本题10分)
(1)证明:如图1 在⊙0中
∵ ∴弧。。。。。。2分
∴。。。
(2)证明:如图2
∵ ∴ 又∵ ∴。。。。。1分又
∵ ∴。。。。。。。。。。1分
∴。。
(3)解:如图3 连接OB,令,则
∵AC是⊙O的直径 ∴。。。。。1分
又∵ ∴ 又∵ ∴
∴。。。。1分
∴弧弧DC ∴ ∴ ∴
∴O
在Rt△OBE中,
在Rt△BCE中,
∴。。。。。。1分
解得(舍) ∴
在Rt△ABE中,。。。。。。。。。1分
27.(本题10分)
解:(1)∵抛物线经过点A(-3,0)
∴ 解得。。。。。。1分
∴抛物线的解析式为 当时, ∴C(0,)
当时, 解得 ∴B(3,0)
在Rt△AOC中, ∴ ∵
∴
∴
∴。。。。。。。。。。1分
(2)如图1
当时, ∴t。。。。。。1分
∴ 当时, 解得
∴D(t,0) ∴OD=t。。。。。1分
∴。。。。。。。1分
(3)如图2,过点K作轴,轴,垂足分别为点N,P。
∵点K在抛物线上,且点K的横坐标为-2
∴点K的纵坐标为 ∴K(-2,)。。。。。。。。1分
∵ ∴四边形KPON是矩形 ∴
∴,
延长AC至点M,使,连接BM,FM。
∵
∴△BCM是等边三角形
∴
∵线段CD绕点C逆时针旋转,得到线段CF
∴,
∴,∴。。。。。。。。。。。。1分
∴ ∵ ∴
∴。。。。。。。。。。。1分
∴
∴
∵
∴又
∵
∴
∴
∴,令
∴
∵
∴
∴
又∵∴。。。。。1分
∴
在Rt△EKN中,,在Rt△OCD中,
∴,∴
∴
解得
∴。。。。。。。。。。1分
(以上各解答题如有不同解法并且正确,请按相应步骤给分)
数学试卷
考生须知:
1. 本试卷满分为120分,考试时间为120分钟。
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内。
3. 请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。
4. 选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
5.保持卡面整洁,不要折叠、不要弄脏、不要弄皱,不准使用涂改液、修正带、刮纸刀。
第I卷 选择题(共30分)(涂卡)
一、选择题(每小题3分,共计30分)
1. 在实数-2,0,,2中,为负实数的是( )
A. -2 B.0 C. D.2
2.下列计算正确的是( )。
A. B.
C. D.
3.下列四种图形中,对称轴条数最多的是( )
A.等边三角形 B.长方形 C.正方形 D.圆
4. 如图所示的几何体是由5个完全相同的小正方体组成,它的主视图是( )
5.在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )
A. B. C. D.
6. 分式方程的解是( )。
A. B. C. D.
7. 如图,在⊙O中,AB切⊙O于点A,连接OB交⊙O于点C,过点A作交⊙O于点D,连接CD.若,则∠OCD的度数为( )。
A. B. C. D.
8.小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )。
A. B.
C. D.
9. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上。若线段,则线段BC的长是( )。
A. B.1 C. D.2
10.一辆汽车行驶30km后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶1h到达目的地。汽车行驶的时间x(单位:h)与行驶的路程y(单位:km)之间的关系如图所示。请结合图象,判断以下说法正确的是( )
A.汽车在高速路上行驶了2.5h
B.汽车在高速路上行驶的路程是180km
C.汽车在高速路上行驶的平均速度是72km/h
D.汽车在乡村道路上行驶的平均速度是40km/h
第II卷 非选择题(共90分)
二、填空题(每小题3分,共计30分)
11. 2022年5月14日,编号为B-001J的C919大飞机首飞成功。数据显示,C919大飞机的单价约为65300000元,数据65300000用科学记数法表示为___________。
12.在函数中,自变量x的取值范围是___________。
13. 计算的结果是___________。
14. 把多项式分解因式的结果是___________。
15. 不等式组的解集是___________。
16.若反比例函数的图象经过点(2,-3),则k的值为___________。
17. 在△ABC中,,点D在射线BA上,,连接CD,则∠BCD的大小是___________度。
18.一个不透明的口袋中,有2个红球和4个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个球,摸到红球的概率是___________。
19. 若扇形的弧长为π,半径为,则它的圆心角为___________度。
20.如图,在正方形ABCD中,点E在BC上,连接AE,过点E作交CD于点F,连接AF,,若,则线段EF的长为___________。
三、解答题(其中21-22题各7分,题各8分,题各10分,共计60分)
21.(本题7分)
先化简,再求代数式的值,其中。
22.(本题7分)
如图,在每个小正方形的边长为1个单位长度的网格中,△ABC的顶点均在格点(网格线的交点)上。
(1)将△ABC向右平移5个单位长度得到,画出;
(2)将(1)中的绕点逆时针旋转得到,画出△;
(3)连接,直接写出线段的长。
23.(本题8分)
某学校为丰富课后服务内容,计划开设经典诵读,花样跳绳、电脑编程、国画鉴赏、民族舞蹈五门兴趣课程。为了解学生对这五门兴趣课程的喜爱情况,随机抽取了部分学生进行问卷调查(要求每位学生只能选择一门课程),并将调查结果绘制成如下两幅不完整的统计图。
根据图中信息,完成下列问题:
(1)求本次调查共抽取了多少名学生:
(2)通过计算补全条形统计图;
(3)若全校共有1200名学生,请估计选择“民族舞蹈”课程的学生人数。
24.(本题8分)
已知:在矩形ABCD中,点E,F都在AD上,且,连接BE,CF。
(1)如图1,求证:;
(2)如图2,连接BF,CE,BF交CE于点G,当,且时,在不添加任何辅助线的情况下,请直接写出图2中度数为的四个角。
25.(本题10分)
某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球。已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元。
(1)求篮球和足球的单价分别是多少元;
(2)学校计划采购篮球、足球共50个,且总费用不超过5500元。那么最多采购篮球多少个?
26.(本题10分)
已知:四边形ABCD是⊙O的内接四边形,,连接AC。
(1)如图1,求证:;
(2)如图2,连接BD交AC于点E,点F在AC上,且,过点F作交CD于点G,求证:;
(3)如图3,在(2)的条件下,AC是⊙O的直径,点F在OC上,若求线段AB的长。
27.(本题10分)
已知:在平面直角坐标系中,点O是坐标原点,抛物线交x轴于点A(-3,0)和点B,交y轴于点C,连接AC,BC。
(1)如图1,求∠ACB的度数;
(2)如图2,直线交线段OB于点D,交y轴于点E,连接CD,设△CDE的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,线段CD绕点C逆时针旋转,得到线段CF,连接AF,取线段AF的中点G,连接BF,GC,分别延长BF,CC交于点H。点K在第二象限抛物线上,连接KE,当点K的横坐标为-2时,,求S的值。
2022-2023学年度上学期
九年级数学科参考答案及评分标准
一、选择题(每小题3分,共计30分)
1 2 3 4 5 6 7 8 9 10
A D D A B C B A C D
二、填空题(每小题3分,共计30分)
题号 11 12 13 14 15
答案 6.53×107 y(x-y)2 -3≤x<-1
题号 16 17 18 19 20
答案 -6 10或100 120
三、解答题(其中21-22题各7分,23-24题各8分,题各10分,共计60分)
21.(本题7分)
解:
原式。。。。。。。。。。。1分
。。。。。。2分
。。。。。。。。。。。。1分
∵。。。。。。。。。2分
∴原式。。
22.(本题7分)
解:(1)如图 正确画图。。。。3分
(2)如图 正确画图。。。。3分
(3)。。。。。。。1分
23.(本题8分)
解:(1)。。。。。2分
。。。。。。1分
答:本次调查共抽取了300名学生。
(2)。。。。。。。1分
正确补图。。。。。。1分
(3)。。。。。。2分
答:估计选择“民族舞蹈”课程的学生人数为200人。。。。。。。。。。。。。。1分
24.(本题8分)
(1)证明:如图1 ∵四边形ABCD为矩形 ∴。。。。。。。2分
又∵ ∴。。。。。。。。。1分
∴。。。。。。。。。
(2)如图2 ∠BEF,∠CFE,∠BGC,∠EGE。。
25.(本题10分)
(1)解:设篮球的单价为x元,足球的单价为y元。
根据题意 得。。。。。。。3分
解得。。。。。。。。。。2分
答:篮球的单价为120元,足球的单价为90元。
(2)设采购篮球m个,则采购足球)个。
根据题意 得。。。。。2分
解得。
∵m为整数 ∴m最大取33.。。。。。1分
答:最多采购篮球33个。。。。。。。1分
26.(本题10分)
(1)证明:如图1 在⊙0中
∵ ∴弧。。。。。。2分
∴。。。
(2)证明:如图2
∵ ∴ 又∵ ∴。。。。。1分又
∵ ∴。。。。。。。。。。1分
∴。。
(3)解:如图3 连接OB,令,则
∵AC是⊙O的直径 ∴。。。。。1分
又∵ ∴ 又∵ ∴
∴。。。。1分
∴弧弧DC ∴ ∴ ∴
∴O
在Rt△OBE中,
在Rt△BCE中,
∴。。。。。。1分
解得(舍) ∴
在Rt△ABE中,。。。。。。。。。1分
27.(本题10分)
解:(1)∵抛物线经过点A(-3,0)
∴ 解得。。。。。。1分
∴抛物线的解析式为 当时, ∴C(0,)
当时, 解得 ∴B(3,0)
在Rt△AOC中, ∴ ∵
∴
∴
∴。。。。。。。。。。1分
(2)如图1
当时, ∴t。。。。。。1分
∴ 当时, 解得
∴D(t,0) ∴OD=t。。。。。1分
∴。。。。。。。1分
(3)如图2,过点K作轴,轴,垂足分别为点N,P。
∵点K在抛物线上,且点K的横坐标为-2
∴点K的纵坐标为 ∴K(-2,)。。。。。。。。1分
∵ ∴四边形KPON是矩形 ∴
∴,
延长AC至点M,使,连接BM,FM。
∵
∴△BCM是等边三角形
∴
∵线段CD绕点C逆时针旋转,得到线段CF
∴,
∴,∴。。。。。。。。。。。。1分
∴ ∵ ∴
∴。。。。。。。。。。。1分
∴
∴
∵
∴又
∵
∴
∴
∴,令
∴
∵
∴
∴
又∵∴。。。。。1分
∴
在Rt△EKN中,,在Rt△OCD中,
∴,∴
∴
解得
∴。。。。。。。。。。1分
(以上各解答题如有不同解法并且正确,请按相应步骤给分)
同课章节目录
