湖南省湘潭市凤凰中学2013-2014学年高二下学期第一次月考数学(文)试题(无答案)
文档属性
| 名称 | 湖南省湘潭市凤凰中学2013-2014学年高二下学期第一次月考数学(文)试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-04 00:00:00 | ||
图片预览

文档简介
第一部分:学业水平(满分100分)
一、选择题:本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则等于( )
A. B. C. D.
2.若函数,则等于( )
A.3 B.6 C.9 D.
3.直线与直线的交点坐标为( )
A. B. C. D.
4.两个球的体积之比为8:27,那么这两个球的表面积之比为( )
A. B. C. D.
5.已知函数,则是( )
A.奇函数 B.偶函数 C.非奇非偶函数 D.既是奇函数又是偶函数
6.向量,,则( )
A. B.
C.与的夹角为 D.与的夹角为
7.已知等差数列中,,,则的值是( )
A.15 B.30 C.31 D.64
8.阅读下面的流程图,若输入的,,分别是5,2,6,则输出的,,分别是( )
A.6,5,2 B.5,2,6
C.2,5,6 D.6,2,5
9.已知函数在区间(2,4)内有唯一零点,则的取值范围是( )
A.R B. C. D.
10.在中,已知,,,则等于( )
A. B.
C. D.
二、填空题:本大题共5小题,每小题4分,满分20分.
11.某校有高级教师20人,中级教师30人,其他教师若干人,为了了解该校教
师的工资收入情况,拟按分层抽样的方法从该校所有的教师中抽取20人进行调
查.已知从其他教师中共抽取了10人,则该校共有教师 人.
12.的值是 .
13.已知,,且,则的最大值是 .
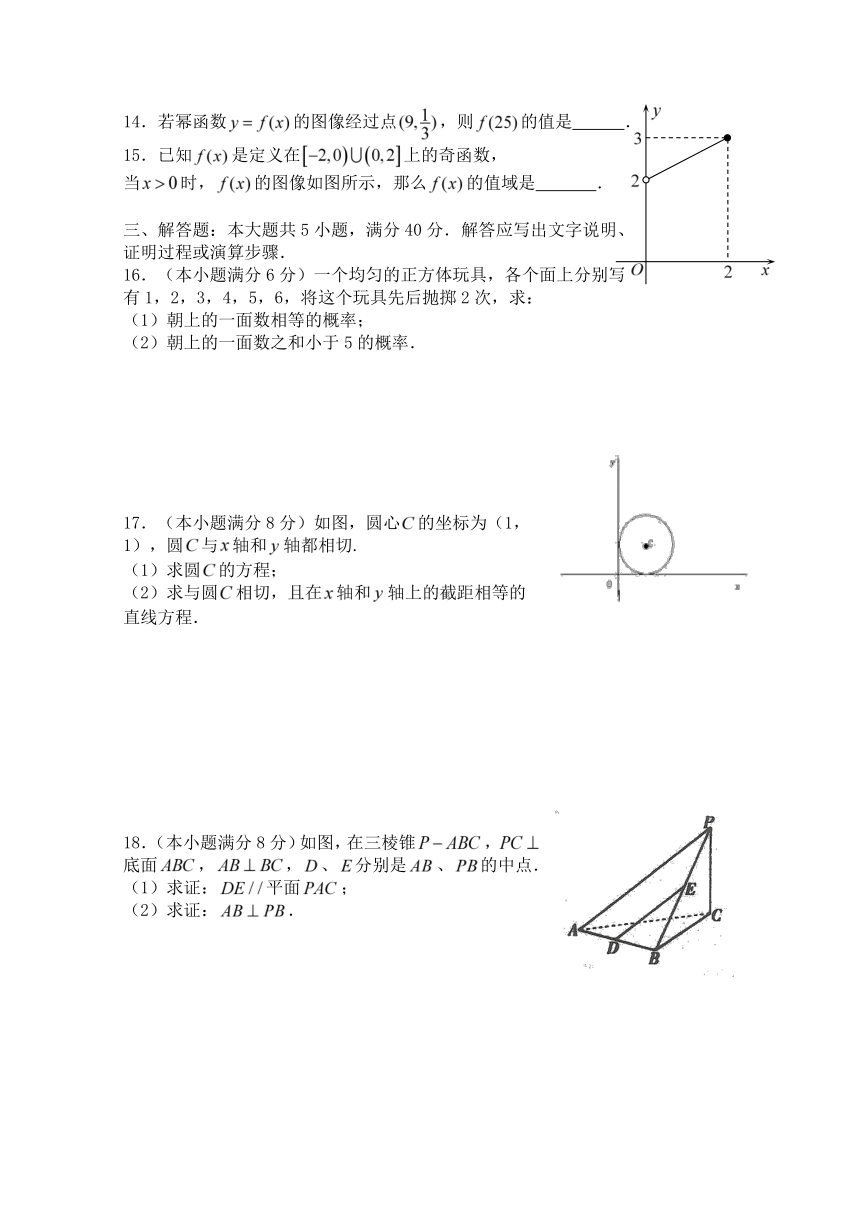
14.若幂函数的图像经过点,则的值是 .
15.已知是定义在上的奇函数,
当时,的图像如图所示,那么的值域是 .
三、解答题:本大题共5小题,满分40分.解答应写出文字说明、
证明过程或演算步骤.
16.(本小题满分6分)一个均匀的正方体玩具,各个面上分别写
有1,2,3,4,5,6,将这个玩具先后抛掷2次,求:
(1)朝上的一面数相等的概率;
(2)朝上的一面数之和小于5的概率.
17.(本小题满分8分)如图,圆心的坐标为(1,1),圆与轴和轴都相切.
(1)求圆的方程;
(2)求与圆相切,且在轴和轴上的截距相等的直线方程.
18.(本小题满分8分)如图,在三棱锥,底面,,、分别是、的中点.
(1)求证:平面;
(2)求证:.
19.(本小题满分8分)已知数列的前项和为.
(1)求数列的通项公式;
(2)若,求数列的前项和为.
20.(本小题满分10分)设函数,其中向量,.
(1)求的最小正周期;
(2)当时,恒成立,求实数的取值范围.
第二部分:能力部分(50分)
21.(5分)若曲线y=x4的一条切线l与直线x+4y-8=0垂直,则l的方程为
22.(5分)函数f(x)=x-ln x的单调减区间为
23.(5分)函数在内有极小值,则实数的取值范围为( )
A.(0,3) B. C. D.
24. (5分)设是椭圆的左、右焦点,为直线上一点,是底角为的等腰三角形,则的离心率为( )
25.(15分)已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A、B两点,点O为坐标原点。
(1)证明:∠AOB为钝角;
(2)若△AOB的面积为4,求直线l的方程。
26. (15分)设函数在及时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的,都有成立,求c的取值范围.
同课章节目录
