2022-2023学年华东师大版九年级数学下册 26.2二次函数的图像与性质 专题练习(无答案)
文档属性
| 名称 | 2022-2023学年华东师大版九年级数学下册 26.2二次函数的图像与性质 专题练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 303.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 16:12:38 | ||
图片预览



文档简介
26.2二次函数的图像与性质专题练习
班级:________ 姓名:________
一、单选题(共 8 小题)
1、已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法错误的是( )
x … ﹣1 0 1 3 …
y … ﹣3 1 3 1 …
A.a<0
B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0
D.若点(5,y1)、(﹣,y2)都在函数图象上,则y1<y2
2、小明在研究抛物线(h为常数)时,得到如下结论,其中正确的是( )
A.无论x取何实数,y的值都小于0
B.该抛物线的顶点始终在直线上
C.当时,y随x的增大而增大,则
D.该抛物线上有两点,,若,,则
3、如图,抛物线过点,,顶点在第四象限,记,则P的取值范围是( )
B. C. D.不能确定
4、抛物线可由抛物线如何平移得到的( )
A.先向左平移3个单位,再向下平移2个单位
B.先向左平移6个单位,再向上平移7个单位
C.先向上平移2个单位,再向左平移3个单位
D.先回右平移3个单位,再向上平移2个单位
5、已知抛物线(a,b,c是常数,)经过点,有下列结论:
①;
②当时,y随x的增大而增大;
③关于x的方程有两个不相等的实数根.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6、甲、乙、丙三人共同探究代数式的情况,三人的说法如下:
甲:只有当时,代数式的值为2;
乙:当x取大于2的实数时,代数式的值随x的增大而减小;
丙:无论x取何值时,代数式的值都不可能大于4.
下列判断正确的是( )
A.甲对,乙对 B.甲对,丙对 C.甲错,丙对 D.乙错,丙错
7、如图,在平面直角坐标系中,二次函数的图像与x轴交于A、C两点,与x轴交于点,若P是x轴上一动点,点D的坐标为,连接PD,则的最小值是( )
A.4 B. C. D.
8、将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2,抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).
A.y=x2-2 B.y=-x2+2 C.y=x2+2 D.y=-x2-2
二、填空题(共 8 小题)
1、已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 _____.
2、已知二次函数y=x2+bx+c的顶点在x轴上,点A(m﹣1,n)和点B(m+3,n)均在二次函数图象上,求n的值为____.
3、下列关于二次函数(为常数)的结论,①该函数的图象与函数的图象形状相同;②该函数的图象一定经过点;③当时,y随x的增大而减小;④该函数的图象的顶点在函数的图像上,其中所有正确的结论序号是__________.
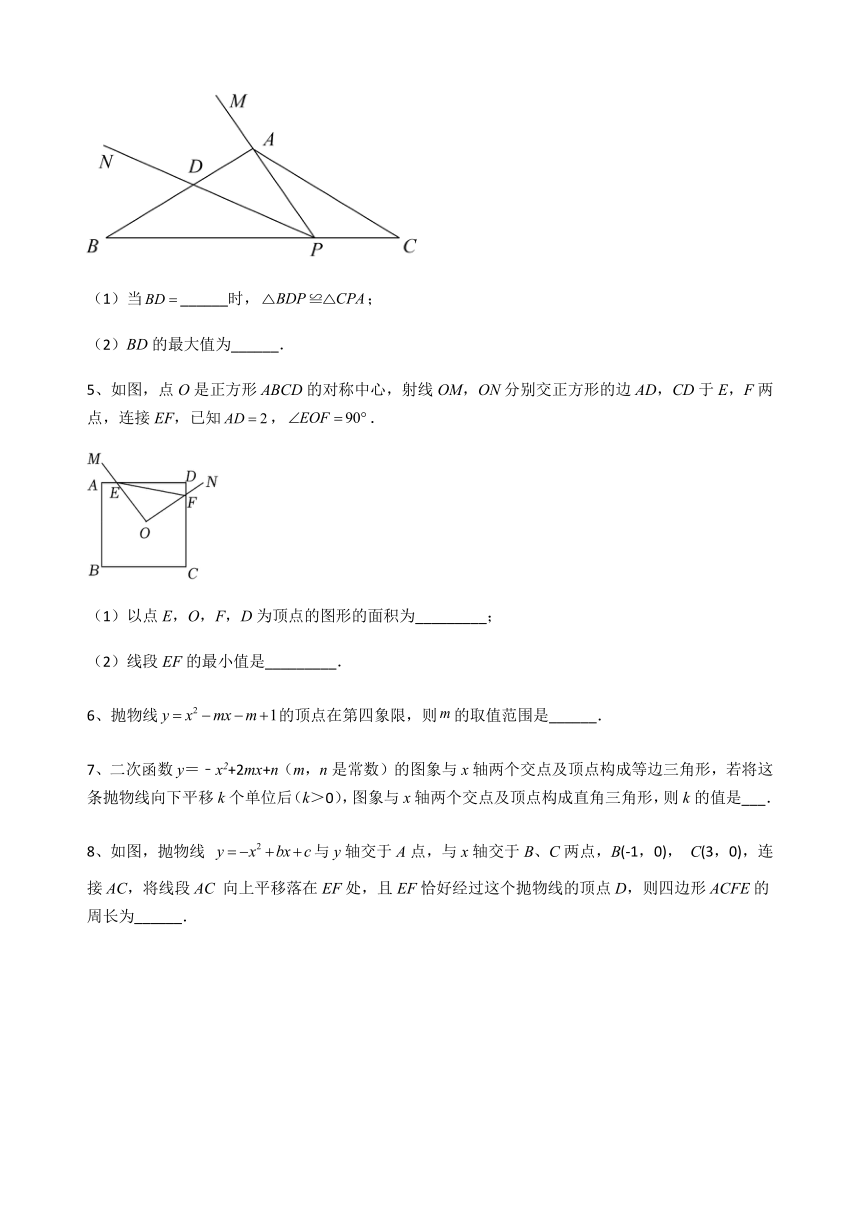
4、在中,,,的顶点P在BC上滑动,PM始终过点A,且,在点P滑动的过程中:
(1)当______时,;
(2)BD的最大值为______.
5、如图,点O是正方形ABCD的对称中心,射线OM,ON分别交正方形的边AD,CD于E,F两点,连接EF,已知,.
(1)以点E,O,F,D为顶点的图形的面积为_________;
(2)线段EF的最小值是_________.
6、抛物线的顶点在第四象限,则的取值范围是______.
7、二次函数y=﹣x2+2mx+n(m,n是常数)的图象与x轴两个交点及顶点构成等边三角形,若将这条抛物线向下平移k个单位后(k>0),图象与x轴两个交点及顶点构成直角三角形,则k的值是___.
8、如图,抛物线 与y轴交于A点,与x轴交于B、C两点,B(-1,0), C(3,0),连接AC,将线段AC 向上平移落在EF处,且EF恰好经过这个抛物线的顶点D,则四边形ACFE的周长为______.
三、解答题(共 5 小题)
1、已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.
(1)求抛物线的解析式;
(2)请画出抛物线的图象;
(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
2、如图,已知二次函数的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)求这个二次函数的对称轴、顶点坐标;
(3)设该二次函数的对称轴与x轴交于点C,连结BA、BC,求△ABC的面积.
3、如图,二次函数(a为常数)的图象的对称轴为直线.
(1)求a的值.
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
4、在平面直角坐标系中,设二次函数(a,b是常数,).
(1)若,当时,.求y的函数表达式.
(2)写出一题a,b的值,使函数的图象与x轴只有一个公共点,并求此函数的顶点坐标.
(3)已知,二次函数的图象和直线都经过点(2,m),求证.
5、已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M.
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
班级:________ 姓名:________
一、单选题(共 8 小题)
1、已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法错误的是( )
x … ﹣1 0 1 3 …
y … ﹣3 1 3 1 …
A.a<0
B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0
D.若点(5,y1)、(﹣,y2)都在函数图象上,则y1<y2
2、小明在研究抛物线(h为常数)时,得到如下结论,其中正确的是( )
A.无论x取何实数,y的值都小于0
B.该抛物线的顶点始终在直线上
C.当时,y随x的增大而增大,则
D.该抛物线上有两点,,若,,则
3、如图,抛物线过点,,顶点在第四象限,记,则P的取值范围是( )
B. C. D.不能确定
4、抛物线可由抛物线如何平移得到的( )
A.先向左平移3个单位,再向下平移2个单位
B.先向左平移6个单位,再向上平移7个单位
C.先向上平移2个单位,再向左平移3个单位
D.先回右平移3个单位,再向上平移2个单位
5、已知抛物线(a,b,c是常数,)经过点,有下列结论:
①;
②当时,y随x的增大而增大;
③关于x的方程有两个不相等的实数根.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6、甲、乙、丙三人共同探究代数式的情况,三人的说法如下:
甲:只有当时,代数式的值为2;
乙:当x取大于2的实数时,代数式的值随x的增大而减小;
丙:无论x取何值时,代数式的值都不可能大于4.
下列判断正确的是( )
A.甲对,乙对 B.甲对,丙对 C.甲错,丙对 D.乙错,丙错
7、如图,在平面直角坐标系中,二次函数的图像与x轴交于A、C两点,与x轴交于点,若P是x轴上一动点,点D的坐标为,连接PD,则的最小值是( )
A.4 B. C. D.
8、将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2,抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).
A.y=x2-2 B.y=-x2+2 C.y=x2+2 D.y=-x2-2
二、填空题(共 8 小题)
1、已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 _____.
2、已知二次函数y=x2+bx+c的顶点在x轴上,点A(m﹣1,n)和点B(m+3,n)均在二次函数图象上,求n的值为____.
3、下列关于二次函数(为常数)的结论,①该函数的图象与函数的图象形状相同;②该函数的图象一定经过点;③当时,y随x的增大而减小;④该函数的图象的顶点在函数的图像上,其中所有正确的结论序号是__________.
4、在中,,,的顶点P在BC上滑动,PM始终过点A,且,在点P滑动的过程中:
(1)当______时,;
(2)BD的最大值为______.
5、如图,点O是正方形ABCD的对称中心,射线OM,ON分别交正方形的边AD,CD于E,F两点,连接EF,已知,.
(1)以点E,O,F,D为顶点的图形的面积为_________;
(2)线段EF的最小值是_________.
6、抛物线的顶点在第四象限,则的取值范围是______.
7、二次函数y=﹣x2+2mx+n(m,n是常数)的图象与x轴两个交点及顶点构成等边三角形,若将这条抛物线向下平移k个单位后(k>0),图象与x轴两个交点及顶点构成直角三角形,则k的值是___.
8、如图,抛物线 与y轴交于A点,与x轴交于B、C两点,B(-1,0), C(3,0),连接AC,将线段AC 向上平移落在EF处,且EF恰好经过这个抛物线的顶点D,则四边形ACFE的周长为______.
三、解答题(共 5 小题)
1、已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.
(1)求抛物线的解析式;
(2)请画出抛物线的图象;
(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
2、如图,已知二次函数的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)求这个二次函数的对称轴、顶点坐标;
(3)设该二次函数的对称轴与x轴交于点C,连结BA、BC,求△ABC的面积.
3、如图,二次函数(a为常数)的图象的对称轴为直线.
(1)求a的值.
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
4、在平面直角坐标系中,设二次函数(a,b是常数,).
(1)若,当时,.求y的函数表达式.
(2)写出一题a,b的值,使函数的图象与x轴只有一个公共点,并求此函数的顶点坐标.
(3)已知,二次函数的图象和直线都经过点(2,m),求证.
5、已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M.
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
