5.3.1导数的应用3:已知函数单调区间求参数范围练习题-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(含答案)
文档属性
| 名称 | 5.3.1导数的应用3:已知函数单调区间求参数范围练习题-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 400.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 00:00:00 | ||
图片预览

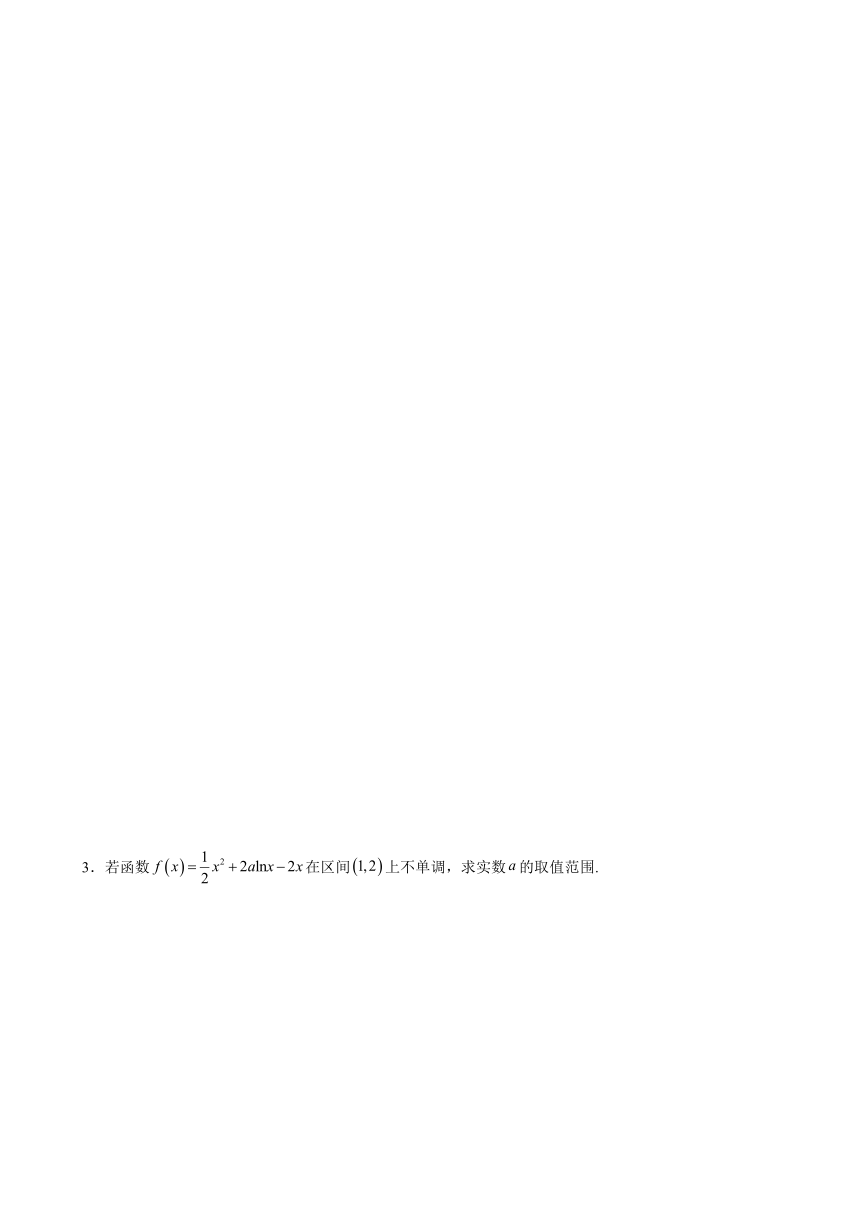



文档简介
5.3.1求导法在单调性的应用3:已知函数单调区间求参数范围
一、单调与不单调
1.若函数在定义域内的一个子区间上不是单调函数,求实数a的取值范围.
2.若函数在区间上不单调,求实数a的取值范围.
3.若函数在区间上不单调,求实数的取值范围.
二、恒成立的知增减
4.若函数在上单调递减,则实数m的取值范围.
5.若函数在上单调递增,求实数a的取值范围.
6.若函数在区间上为减函数,求实数的取值范围.
7.若函数在定义域内单调递减,求实数的取值范围.
8.若函数在区间上是减函数,求实数a的取值范围.
三、恒成立的需再求导
9.若函数在上单调递增,求实数的取值范围.
10.若函数在上单调递增,求实数的取值范围.
11.若函数在上单调递减,求实数的取值范围.
12.若在上单调递增,求实数的取值范围.
四、先构造函数
13.若函数,,使得,求的取值范围.
14.若函数,对任意的,有恒成立,求的取值范围.
15.若函数,对于内的任意两个数,当时,恒成立,求实数的取值范围.
16.若对于,且,都有,求的取值范围.
5.3.1求导法在单调性的应用3:已知函数单调区间求参数范围参考答案
1.【解】定义域为,,
令,得时;令,得
∴在上递增,在上递减
要想在子区间上不是单调函数,则,解得,.
2.【解】定义域为,∴,又,令,得;令,得
∴在上递减,在上递增
∵在区间上不单调,∴,即,
∴,即,又,∴
3.【解】(1)定义域为,
令,其对称轴为,
∵函数在区间上不单调,∴即,解得.
4.【解】,∵函数在区间上递减,
∴对于恒成立,即:对于,.
又在上递减,∴,∴,即
5.【解】,若在上递增,则恒成立,,即
6.【解】,∵在区间上为减函数,且在端点处有定义,
∴对于恒成立,即对于恒成立,∴
∵在上递减,∴当时,,∴.
7.【解】】定义域为,,
又在定义域内递减,在上恒成立,即在上恒成立
,
8.【解】∵,在区间上是减函数,∴对任意恒成立,
即对任意恒成立,令,则,
∵函数在上都是减函数,∴函数在上递减,∴,∴
9【解】∵在上递增,∴在恒成立,∴,
令,则,
令,解得,令,解得,∴在上递减,在上递增,
∴,∴的取值范围是.
10.【解】∵,则,
∵函数在上递增,则对任意的恒成立,
即对任意的恒成立,
当时,,则,∴.
11.【解】定义域为,,令
在上递减,∴在上恒成立,∴在上恒成立
则,令,得;令,得
在上递增,在上递减,∴,∴.
12.【解】∵在上递增,∴在上恒成立,且不恒等于
令,得,
令,则,∴在上递减,
∴
13.【解】不妨设, ∵,即,即,
构造函数,∴在递增,∴,
∴
∵当时,,,∴,∴,
∴的取值范围为
14.【解】∵,∴,
∴在上递增,
∵,∴在上恒成立,
∴,即在上恒成立,
∵
∴,即实数的取值范围为.
15.【解】∵,即,
设,则在上为减函数,
则 对恒成立,
可得在上恒成立.
令, ,
则在上递减,∴,∴,即
16.【解】∵是R上的增函数,∴当,时, ,
若有 ,
即 ,即,
即,
令,则在上递增,
又,令,得,则的单调增区间为,
∴,即有,∴的取值范围是
一、单调与不单调
1.若函数在定义域内的一个子区间上不是单调函数,求实数a的取值范围.
2.若函数在区间上不单调,求实数a的取值范围.
3.若函数在区间上不单调,求实数的取值范围.
二、恒成立的知增减
4.若函数在上单调递减,则实数m的取值范围.
5.若函数在上单调递增,求实数a的取值范围.
6.若函数在区间上为减函数,求实数的取值范围.
7.若函数在定义域内单调递减,求实数的取值范围.
8.若函数在区间上是减函数,求实数a的取值范围.
三、恒成立的需再求导
9.若函数在上单调递增,求实数的取值范围.
10.若函数在上单调递增,求实数的取值范围.
11.若函数在上单调递减,求实数的取值范围.
12.若在上单调递增,求实数的取值范围.
四、先构造函数
13.若函数,,使得,求的取值范围.
14.若函数,对任意的,有恒成立,求的取值范围.
15.若函数,对于内的任意两个数,当时,恒成立,求实数的取值范围.
16.若对于,且,都有,求的取值范围.
5.3.1求导法在单调性的应用3:已知函数单调区间求参数范围参考答案
1.【解】定义域为,,
令,得时;令,得
∴在上递增,在上递减
要想在子区间上不是单调函数,则,解得,.
2.【解】定义域为,∴,又,令,得;令,得
∴在上递减,在上递增
∵在区间上不单调,∴,即,
∴,即,又,∴
3.【解】(1)定义域为,
令,其对称轴为,
∵函数在区间上不单调,∴即,解得.
4.【解】,∵函数在区间上递减,
∴对于恒成立,即:对于,.
又在上递减,∴,∴,即
5.【解】,若在上递增,则恒成立,,即
6.【解】,∵在区间上为减函数,且在端点处有定义,
∴对于恒成立,即对于恒成立,∴
∵在上递减,∴当时,,∴.
7.【解】】定义域为,,
又在定义域内递减,在上恒成立,即在上恒成立
,
8.【解】∵,在区间上是减函数,∴对任意恒成立,
即对任意恒成立,令,则,
∵函数在上都是减函数,∴函数在上递减,∴,∴
9【解】∵在上递增,∴在恒成立,∴,
令,则,
令,解得,令,解得,∴在上递减,在上递增,
∴,∴的取值范围是.
10.【解】∵,则,
∵函数在上递增,则对任意的恒成立,
即对任意的恒成立,
当时,,则,∴.
11.【解】定义域为,,令
在上递减,∴在上恒成立,∴在上恒成立
则,令,得;令,得
在上递增,在上递减,∴,∴.
12.【解】∵在上递增,∴在上恒成立,且不恒等于
令,得,
令,则,∴在上递减,
∴
13.【解】不妨设, ∵,即,即,
构造函数,∴在递增,∴,
∴
∵当时,,,∴,∴,
∴的取值范围为
14.【解】∵,∴,
∴在上递增,
∵,∴在上恒成立,
∴,即在上恒成立,
∵
∴,即实数的取值范围为.
15.【解】∵,即,
设,则在上为减函数,
则 对恒成立,
可得在上恒成立.
令, ,
则在上递减,∴,∴,即
16.【解】∵是R上的增函数,∴当,时, ,
若有 ,
即 ,即,
即,
令,则在上递增,
又,令,得,则的单调增区间为,
∴,即有,∴的取值范围是
