5.7三角函数的应用课时练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案)
文档属性
| 名称 | 5.7三角函数的应用课时练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 672.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 14:02:40 | ||
图片预览

文档简介
高一数学必修一5.7《三角函数的应用》课时练习
一、选择题:
1、如图所示,单摆从某点开始来回摆动,离开平衡位置O的距离s(cm)和时间t(s)的函数关系式为s=6sin,那么单摆摆动一个周期所需的时间为( )
A.2π s B.π s C.0.5 s D.1 s
2、函数的周期,振幅,初相分别是( )
A. B. C. D.
3、红河州个旧市是一个风景优美的宜居城市,如图是个旧宝华公园的摩天轮,半径为20米,圆心O距地面的高度为25米,摩天轮运行时按逆时针匀速旋转,转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底,则摩天轮转动一周内具有最佳视觉效果的时间长度(单位:分钟)为( )
A. B.3 C. D.
4、如图所示,是函数y=Asin(, (A>0,的简图,则振幅、周期、初相分别是( )
A.2,, B.2,, C.4,, D.2,,
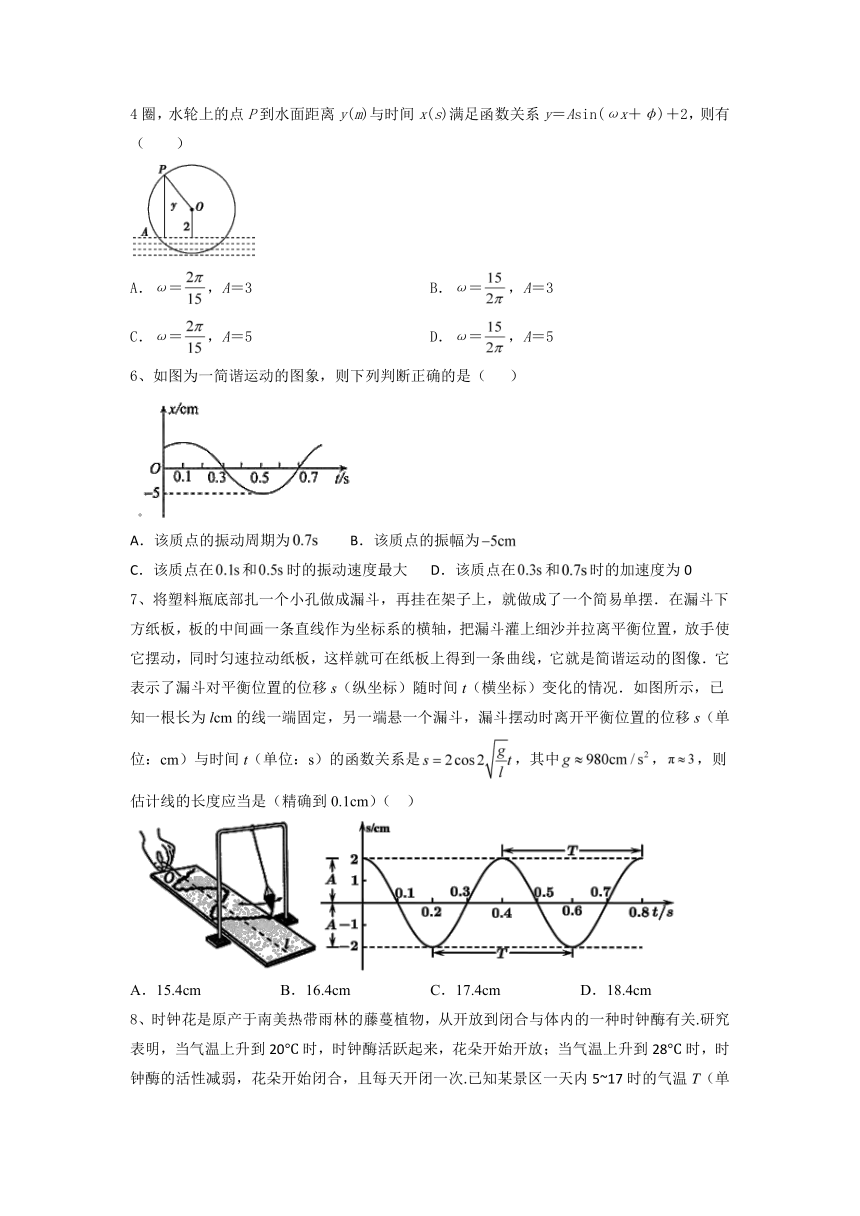
5、如图,为一半径为3m的水轮,水轮圆心O距离水面2m,已知水轮自点A开始1min旋转4圈,水轮上的点P到水面距离y(m)与时间x(s)满足函数关系y=Asin(ωx+φ)+2,则有( )
A.ω=,A=3 B.ω=,A=3
C.ω=,A=5 D.ω=,A=5
6、如图为一简谐运动的图象,则下列判断正确的是( )
A.该质点的振动周期为 B.该质点的振幅为
C.该质点在和时的振动速度最大 D.该质点在和时的加速度为0
7、将塑料瓶底部扎一个小孔做成漏斗,再挂在架子上,就做成了一个简易单摆.在漏斗下方纸板,板的中间画一条直线作为坐标系的横轴,把漏斗灌上细沙并拉离平衡位置,放手使它摆动,同时匀速拉动纸板,这样就可在纸板上得到一条曲线,它就是简谐运动的图像.它表示了漏斗对平衡位置的位移s(纵坐标)随时间t(横坐标)变化的情况.如图所示,已知一根长为lcm的线一端固定,另一端悬一个漏斗,漏斗摆动时离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系是,其中,,则估计线的长度应当是(精确到0.1cm)( )
A.15.4cm B.16.4cm C.17.4cm D.18.4cm
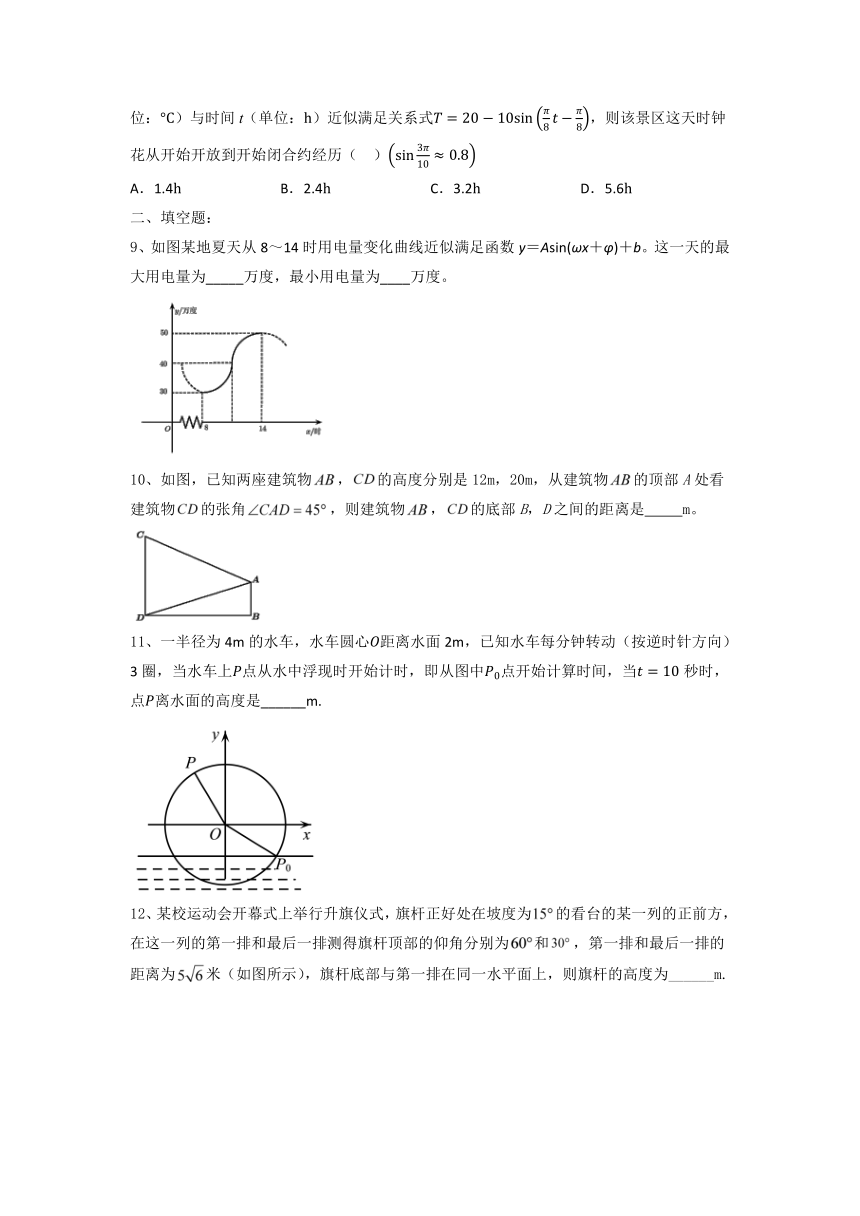
8、时钟花是原产于南美热带雨林的藤蔓植物,从开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20时,时钟酶活跃起来,花朵开始开放;当气温上升到28时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17时的气温T(单位:)与时间t(单位:)近似满足关系式,则该景区这天时钟花从开始开放到开始闭合约经历( )
A.1.4 B.2.4 C.3.2 D.5.6
二、填空题:
9、如图某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b。这一天的最大用电量为_____万度,最小用电量为____万度。
10、如图,已知两座建筑物,的高度分别是12m,20m,从建筑物的顶部A处看建筑物的张角,则建筑物,的底部B,D之间的距离是 m。
11、一半径为4m的水车,水车圆心距离水面2m,已知水车每分钟转动(按逆时针方向)3圈,当水车上点从水中浮现时开始计时,即从图中点开始计算时间,当秒时,点离水面的高度是______m.
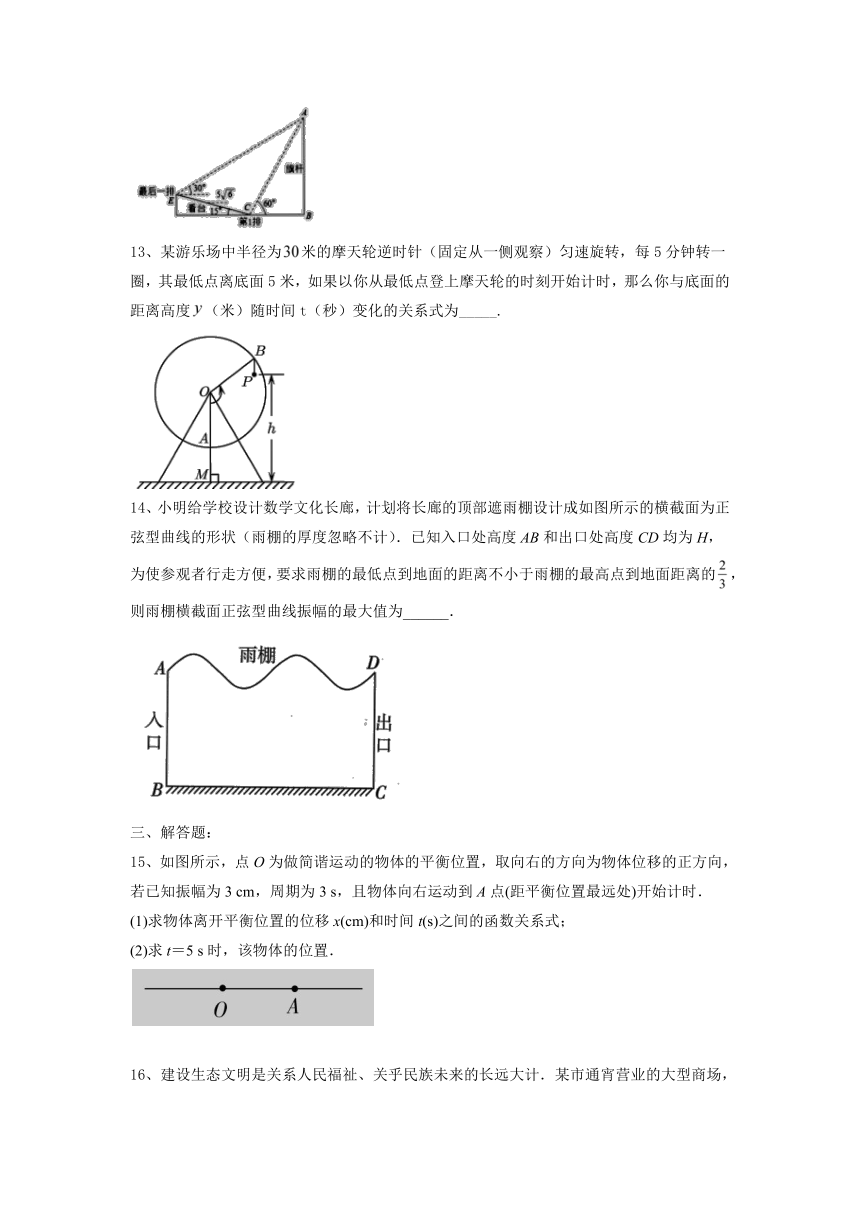
12、某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度为的看台的某一列的正前方,在这一列的第一排和最后一排测得旗杆顶部的仰角分别为和,第一排和最后一排的距离为米(如图所示),旗杆底部与第一排在同一水平面上,则旗杆的高度为______m.
13、某游乐场中半径为米的摩天轮逆时针(固定从一侧观察)匀速旋转,每5分钟转一圈,其最低点离底面5米,如果以你从最低点登上摩天轮的时刻开始计时,那么你与底面的距离高度(米)随时间t(秒)变化的关系式为_____.
14、小明给学校设计数学文化长廊,计划将长廊的顶部遮雨棚设计成如图所示的横截面为正弦型曲线的形状(雨棚的厚度忽略不计).已知入口处高度AB和出口处高度CD均为H,为使参观者行走方便,要求雨棚的最低点到地面的距离不小于雨棚的最高点到地面距离的,则雨棚横截面正弦型曲线振幅的最大值为______.
三、解答题:
15、如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3 cm,周期为3 s,且物体向右运动到A点(距平衡位置最远处)开始计时.
(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式;
(2)求t=5 s时,该物体的位置.
16、建设生态文明是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应国家节能减排的号召,在气温低于时,才开放中央空调,否则关闭中央空调.如图是该市冬季某一天的气温(单位:)随时间t(,单位:小时)的大致变化曲线,若该曲线近似满足关系.
(1)求的表达式;
(2)请根据(1)的结论,求该商场的中央空调在一天内开启的时长.
17、一半径为的水轮(如图所示),水轮圆心O离水面,已知水轮逆时针转动,每转一圈,且当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)试建立适当的坐标系,将点P距离水面的高度表示为时间的函数;
(2)点P第一次到达最高点大约要多长时间?
18、弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置厘米有下列关系确定.
(1)以t为横坐标,h为纵坐标,作出这个函数在一个周期内的图象;
(2)小球在开始振动时的位置在哪里?
(3)小球的最高点和最低点与平衡位置的距离分别是多少?
(4)经过多少时间小球往复运动一次?
(5)每秒钟小球能往复振动多少次?
参考答案
一、选择题:
1、 D 2、C 3、C 4、B
5、 A 6、 D 7、C 8、B
二、解答题:
9、 50 30
10、24
11、 4
12、 15
13、
14、 H/5
三、解答题:
15、(1)设位移x(cm)和时间t(s)之间的函数关系式为x=Asin(ωt+φ)(A>0,ω>0,0≤φ<2π),
则由振幅为3 cm,周期为3 s,可得A=3,T==3,得ω=.
又向右运动到A点(距平衡位置最远处)开始计时,∴当t=0时,x=3sinφ=3,∴sinφ=1.
∵0≤φ<2π,∴φ=,从而所求的函数关系式是x=3sin=3cost.
(2)令t=5,得x=3cos=-1.5,故t=5 s时,该物体在O点左侧且距O点1.5 cm处.
16、(1)因为图像上最低点坐标为,与之相邻的最高点坐标为,所以,,,
所以,解得.所以,.
(2)由(1)得,,所以,
所以,解得,
因为,所以,.
所以该商场的中央空调应在本天内开启时长为8小时.
17、(1)解:以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,建立如图所示的直角坐标系,
设,则,,
∵,∴,∴,
∵时,,∴,∴,
∵,∴,∴.
(2)解:令,得,
∴,,∴,,∴当时,P第一次到达最高点,
∴点P第一次到达最高点大约要.
18、(1)由题意可得的图象,
(2)由题意可得当时,,故小球在开始振动时的位置在,
(3)由解析式可得振幅,故小球的最高点和最低点与平衡位置的距离均为2(厘米);
(4)可得函数的周期为,故小球往复运动一次需,
(5)可得频率为,即每秒钟小球能往复振动次
一、选择题:
1、如图所示,单摆从某点开始来回摆动,离开平衡位置O的距离s(cm)和时间t(s)的函数关系式为s=6sin,那么单摆摆动一个周期所需的时间为( )
A.2π s B.π s C.0.5 s D.1 s
2、函数的周期,振幅,初相分别是( )
A. B. C. D.
3、红河州个旧市是一个风景优美的宜居城市,如图是个旧宝华公园的摩天轮,半径为20米,圆心O距地面的高度为25米,摩天轮运行时按逆时针匀速旋转,转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底,则摩天轮转动一周内具有最佳视觉效果的时间长度(单位:分钟)为( )
A. B.3 C. D.
4、如图所示,是函数y=Asin(, (A>0,的简图,则振幅、周期、初相分别是( )
A.2,, B.2,, C.4,, D.2,,
5、如图,为一半径为3m的水轮,水轮圆心O距离水面2m,已知水轮自点A开始1min旋转4圈,水轮上的点P到水面距离y(m)与时间x(s)满足函数关系y=Asin(ωx+φ)+2,则有( )
A.ω=,A=3 B.ω=,A=3
C.ω=,A=5 D.ω=,A=5
6、如图为一简谐运动的图象,则下列判断正确的是( )
A.该质点的振动周期为 B.该质点的振幅为
C.该质点在和时的振动速度最大 D.该质点在和时的加速度为0
7、将塑料瓶底部扎一个小孔做成漏斗,再挂在架子上,就做成了一个简易单摆.在漏斗下方纸板,板的中间画一条直线作为坐标系的横轴,把漏斗灌上细沙并拉离平衡位置,放手使它摆动,同时匀速拉动纸板,这样就可在纸板上得到一条曲线,它就是简谐运动的图像.它表示了漏斗对平衡位置的位移s(纵坐标)随时间t(横坐标)变化的情况.如图所示,已知一根长为lcm的线一端固定,另一端悬一个漏斗,漏斗摆动时离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系是,其中,,则估计线的长度应当是(精确到0.1cm)( )
A.15.4cm B.16.4cm C.17.4cm D.18.4cm
8、时钟花是原产于南美热带雨林的藤蔓植物,从开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20时,时钟酶活跃起来,花朵开始开放;当气温上升到28时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17时的气温T(单位:)与时间t(单位:)近似满足关系式,则该景区这天时钟花从开始开放到开始闭合约经历( )
A.1.4 B.2.4 C.3.2 D.5.6
二、填空题:
9、如图某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b。这一天的最大用电量为_____万度,最小用电量为____万度。
10、如图,已知两座建筑物,的高度分别是12m,20m,从建筑物的顶部A处看建筑物的张角,则建筑物,的底部B,D之间的距离是 m。
11、一半径为4m的水车,水车圆心距离水面2m,已知水车每分钟转动(按逆时针方向)3圈,当水车上点从水中浮现时开始计时,即从图中点开始计算时间,当秒时,点离水面的高度是______m.
12、某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度为的看台的某一列的正前方,在这一列的第一排和最后一排测得旗杆顶部的仰角分别为和,第一排和最后一排的距离为米(如图所示),旗杆底部与第一排在同一水平面上,则旗杆的高度为______m.
13、某游乐场中半径为米的摩天轮逆时针(固定从一侧观察)匀速旋转,每5分钟转一圈,其最低点离底面5米,如果以你从最低点登上摩天轮的时刻开始计时,那么你与底面的距离高度(米)随时间t(秒)变化的关系式为_____.
14、小明给学校设计数学文化长廊,计划将长廊的顶部遮雨棚设计成如图所示的横截面为正弦型曲线的形状(雨棚的厚度忽略不计).已知入口处高度AB和出口处高度CD均为H,为使参观者行走方便,要求雨棚的最低点到地面的距离不小于雨棚的最高点到地面距离的,则雨棚横截面正弦型曲线振幅的最大值为______.
三、解答题:
15、如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3 cm,周期为3 s,且物体向右运动到A点(距平衡位置最远处)开始计时.
(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式;
(2)求t=5 s时,该物体的位置.
16、建设生态文明是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应国家节能减排的号召,在气温低于时,才开放中央空调,否则关闭中央空调.如图是该市冬季某一天的气温(单位:)随时间t(,单位:小时)的大致变化曲线,若该曲线近似满足关系.
(1)求的表达式;
(2)请根据(1)的结论,求该商场的中央空调在一天内开启的时长.
17、一半径为的水轮(如图所示),水轮圆心O离水面,已知水轮逆时针转动,每转一圈,且当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)试建立适当的坐标系,将点P距离水面的高度表示为时间的函数;
(2)点P第一次到达最高点大约要多长时间?
18、弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置厘米有下列关系确定.
(1)以t为横坐标,h为纵坐标,作出这个函数在一个周期内的图象;
(2)小球在开始振动时的位置在哪里?
(3)小球的最高点和最低点与平衡位置的距离分别是多少?
(4)经过多少时间小球往复运动一次?
(5)每秒钟小球能往复振动多少次?
参考答案
一、选择题:
1、 D 2、C 3、C 4、B
5、 A 6、 D 7、C 8、B
二、解答题:
9、 50 30
10、24
11、 4
12、 15
13、
14、 H/5
三、解答题:
15、(1)设位移x(cm)和时间t(s)之间的函数关系式为x=Asin(ωt+φ)(A>0,ω>0,0≤φ<2π),
则由振幅为3 cm,周期为3 s,可得A=3,T==3,得ω=.
又向右运动到A点(距平衡位置最远处)开始计时,∴当t=0时,x=3sinφ=3,∴sinφ=1.
∵0≤φ<2π,∴φ=,从而所求的函数关系式是x=3sin=3cost.
(2)令t=5,得x=3cos=-1.5,故t=5 s时,该物体在O点左侧且距O点1.5 cm处.
16、(1)因为图像上最低点坐标为,与之相邻的最高点坐标为,所以,,,
所以,解得.所以,.
(2)由(1)得,,所以,
所以,解得,
因为,所以,.
所以该商场的中央空调应在本天内开启时长为8小时.
17、(1)解:以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,建立如图所示的直角坐标系,
设,则,,
∵,∴,∴,
∵时,,∴,∴,
∵,∴,∴.
(2)解:令,得,
∴,,∴,,∴当时,P第一次到达最高点,
∴点P第一次到达最高点大约要.
18、(1)由题意可得的图象,
(2)由题意可得当时,,故小球在开始振动时的位置在,
(3)由解析式可得振幅,故小球的最高点和最低点与平衡位置的距离均为2(厘米);
(4)可得函数的周期为,故小球往复运动一次需,
(5)可得频率为,即每秒钟小球能往复振动次
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
