【模块一数与式】专题2 整式与因式分解-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块一数与式】专题2 整式与因式分解-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 844.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 14:26:31 | ||
图片预览




文档简介
2023年中考数学第一轮复习
模块一 数与式
专题2 整式与因式分解
整 式 的 相 关 概 念 单项式 由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数。如:单项式系数是,次数是4。
多项式 几个单项式的和叫做多项式;多项式中,每一个单项式叫做多项式的项,其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数。 如:多项式2+4x2y﹣是五次三项式
整式 整式是单项式与多项式的统称。
同类项 所含字母相同,并且相同字母的指数也分别相同的单项式叫做同类项。
合并同类项 把多项式中的同类项合并成一项叫做合并同类项,合并的法则是系数相加,所得的结果作为合并后的系数,字母和字母的指数不变。
整 式 运 算 幂的运算 同底数幂乘法 am·an=am+n(a≠0) am+n=am·an
同底数幂除法 =am-n(m,n是正整数) am-n=
幂的乘方 (am)n=amn(a≠0) amn=(am)n
积的乘方 (ab)n=anbn anbn=(ab)n
乘法 公式 平方差公式 (a+b)(a-b)=a2-b2 a2-b2=(a+b)(a-b)
完全平方公式 (a±b)2=a2±2ab+b2 a2±2ab+b2=(a±b)2
整式 加减 ① 整式的加减其实就是合并同类项; ② 整式加减的步骤:有括号,先去括号;有同类项,再合并同类项.注意去括号时,如果括号前面是负号,括号里各项的符号要变号.
整式 乘法 ① 单项式与单项式相乘:把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. ② 单项式与多项式相乘:m(a+b+c)=ma+mb+mC. ③ 多项式与多项式相乘:(m+n)(a+b)=ma+mb+na+nb.
整式 除法 ① 单项式除以单项式:把系数、同底数幂相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式. ② 多项式除以单项式:(a+b)÷m=a÷m+b÷m.
因式 分解 概念 把一个多项式化成几个整式积的形式,叫做多项式的因式分解。和的形式变积的形式
因式分解方法 提公因式法 ma+mb+mc=m(a+b+c)(乘法分配律的运用)
公式法 ① 运用平方差公式:a2-b2=(a+b)(a-b). ② 运用完全平方公式:a2±2ab+b2=(a±b)2.
求代数式的值 1.一般地,用数值代替代数式里的字母,按照代数式指明的运算关系计算出的结果就叫做代数式的值. 2.求代数式的值的基本步骤: ① 代入:一般情况下,先对代数式进行化简,再将数值代入; ② 计算:按代数式指明的运算关系计算出结果.
题型一、代数式及其求值
1.(2022·湖南邵阳)已知,则_________.
2.(2022·内蒙古赤峰)已知,则的值为( )
A.13 B.8 C.-3 D.5
3.(2022·湖南长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.元 B.元 C.元 D.元
题型二、整式的有关概念
1.(2022·广东)单项式的系数为___________.
2.(2022·湖南湘潭)下列整式与为同类项的是( )
A. B. C. D.
3.(2022·内蒙古包头)若一个多项式加上,结果得,则这个多项式为___________.
4.(2022·黑龙江大庆)已知代数式是一个完全平方式,则实数t的值为____________.
题型三、整式的运算
1.(2022·江苏宿迁)下列运算正确的是( )
A. B. C. D.
2.(2022·四川眉山)下列运算中,正确的是( )
A. B.
C. D.
3.(2022·浙江绍兴)下列计算正确的是( )
A. B. C. D.
4.(2022·四川成都)下列计算正确的是( )
A. B. C. D.
5.(2022·内蒙古包头)若,则m的值为( )
A.8 B.6 C.5 D.2
题型四、因式分解及其应用
1.(2022·浙江嘉兴)分解因式:m2-1=_____.
2.(2022·湖南怀化)因式分解:_____.
3.(2022·浙江绍兴)分解因式: = ______.
4.(2022·浙江宁波)分解因式:x2-2x+1=__________.
5.(2022·辽宁锦州)分解因式:____________.
6.(2022·江苏常州)分解因式:______.
7.(2022·四川内江)分解因式:a4﹣3a2﹣4=_____.
8.(2022·湖北恩施)因式分解:=_______.
9.(2022·山东临沂)因式分解=______.
10.(2022·四川乐山)已知,则______.
11.(2022·四川广安)已知a+b=1,则代数式a2﹣b2 +2b+9的值为________.
题型五、乘法公式的应用
1.(2022·江苏苏州)已知,,则______.
2.(2022·山东滨州)若,,则的值为_______.
3.(2022·四川德阳)已知(x+y)2=25,(x﹣y)2=9,则xy=___.
4.(2022·广西)如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A. B.
C. D.
题型六、整式的化简求值
1.(2022·湖南衡阳)先化简,再求值:,其中,.
2.(2022·广西)先化简,再求值,其中.
3.(2022·北京)已知,求代数式的值.
4.(2022·吉林长春)先化简,再求值:,其中.
5.(2021·吉林长春)先化简,再求值:,其中.
题型七、数式的规律探究
1.(2022·云南)按一定规律排列的单项式:x,3x ,5x ,7x,9x,……,第n个单项式是( )
A.(2n-1) B.(2n+1) C.(n-1) D.(n+1)
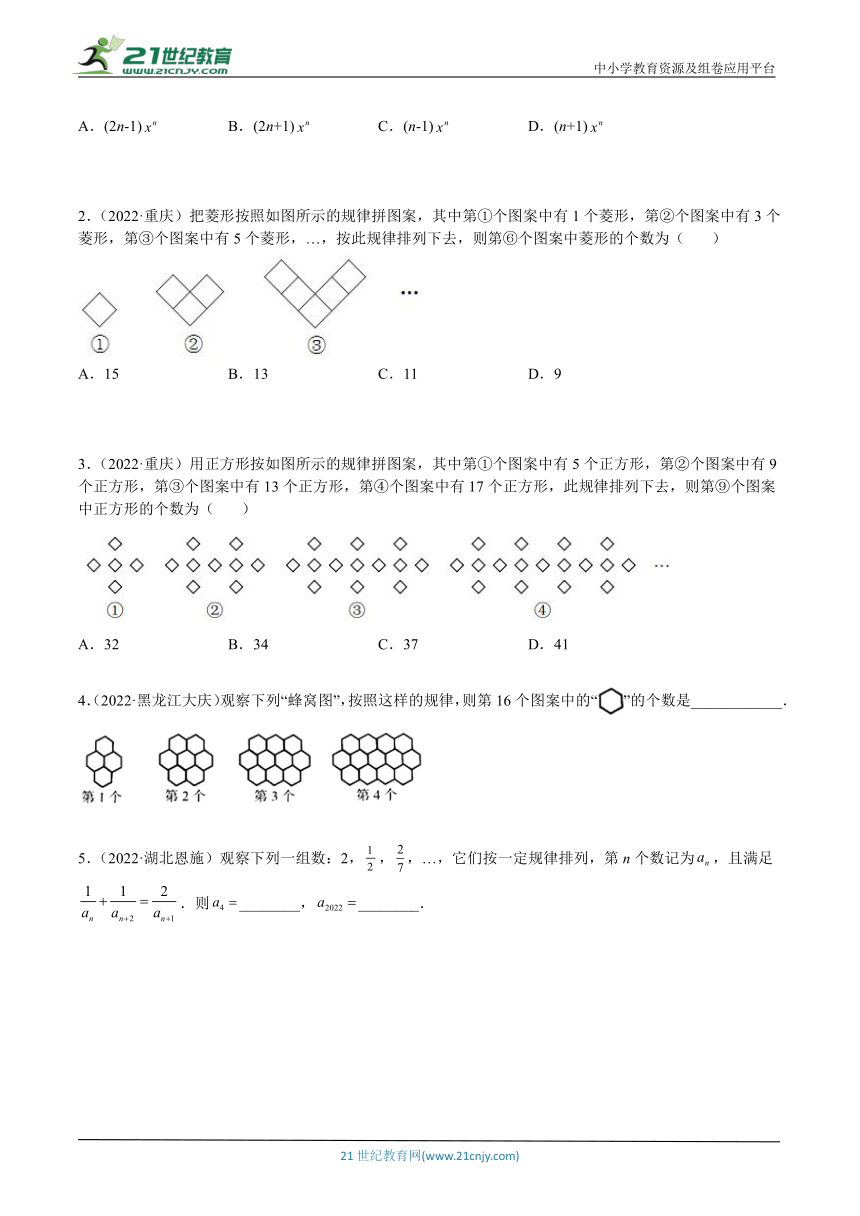
2.(2022·重庆)把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )
A.15 B.13 C.11 D.9
3.(2022·重庆)用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )
A.32 B.34 C.37 D.41
4.(2022·黑龙江大庆)观察下列“蜂窝图”,按照这样的规律,则第16个图案中的“”的个数是____________.
5.(2022·湖北恩施)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为,且满足.则________,________.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
2023年中考数学第一轮复习
模块一 数与式
专题2 整式与因式分解
知识梳理
整 式 的 相 关 概 念 单项式 由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数。 如:单项式系数是,次数是4。
多项式 几个单项式的和叫做多项式;多项式中,每一个单项式叫做多项式的项,其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数。 如:多项式2+4x2y﹣是五次三项式
整式 整式是单项式与多项式的统称。
同类项 所含字母相同,并且相同字母的指数也分别相同的单项式叫做同类项。
合并同类项 把多项式中的同类项合并成一项叫做合并同类项,合并的法则是系数相加,所得的结果作为合并后的系数,字母和字母的指数不变。
整 式 运 算 幂的运算 同底数幂乘法 am·an=am+n(a≠0) am+n=am·an
同底数幂除法 =am-n(m,n是正整数) am-n=
幂的乘方 (am)n=amn(a≠0) amn=(am)n
积的乘方 (ab)n=anbn anbn=(ab)n
乘法 公式 平方差公式 (a+b)(a-b)=a2-b2 a2-b2=(a+b)(a-b)
完全平方公式 (a±b)2=a2±2ab+b2 a2±2ab+b2=(a±b)2
整式 加减 ① 整式的加减其实就是合并同类项; ② 整式加减的步骤:有括号,先去括号;有同类项,再合并同类项.注意去括号时,如果括号前面是负号,括号里各项的符号要变号.
整式 乘法 ① 单项式与单项式相乘:把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. ② 单项式与多项式相乘:m(a+b+c)=ma+mb+mC. ③ 多项式与多项式相乘:(m+n)(a+b)=ma+mb+na+nb.
整式 除法 ① 单项式除以单项式:把系数、同底数幂相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式. ② 多项式除以单项式:(a+b)÷m=a÷m+b÷m.
因式 分解 概念 把一个多项式化成几个整式积的形式,叫做多项式的因式分解。和的形式变积的形式
因式分解方法 提公因式法 ma+mb+mc=m(a+b+c)(乘法分配律的运用)
公式法 ① 运用平方差公式:a2-b2=(a+b)(a-b). ② 运用完全平方公式:a2±2ab+b2=(a±b)2.
求代数式的值 1.一般地,用数值代替代数式里的字母,按照代数式指明的运算关系计算出的结果就叫做代数式的值. 2.求代数式的值的基本步骤: ① 代入:一般情况下,先对代数式进行化简,再将数值代入; ② 计算:按代数式指明的运算关系计算出结果.
题型梳理
题型一、代数式及其求值
1.(2022·湖南邵阳)已知,则_________.
【答案】2
【分析】将变形为即可计算出答案.
【详解】
∵
∴
故答案为:2.
【点睛】本题考查代数式的性质,解题的关键是熟练掌握代数式的相关知识.
2.(2022·内蒙古赤峰)已知,则的值为( )
A.13 B.8 C.-3 D.5
【答案】A
【分析】先化简已知的式子,再整体代入求值即可.
【详解】∵
∴
∴故选:A.
【点睛】本题考查平方差公式、代数式求值,利用整体思想是解题的关键.
3.(2022·湖南长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.元 B.元 C.元 D.元
【答案】C
【分析】根据题意列求得购买乙种读本本,根据单价乘以数量即可求解.
【详解】解:设购买甲种读本x本,则购买乙种读本本,乙种读本的单价为8元/本,则则购买乙种读本的费用为元故选C
【点睛】本题考查了列代数式,理解题意是解题的关键.
题型二、整式的有关概念
1.(2022·广东)单项式的系数为___________.
【答案】3
【分析】单项式中数字因数叫做单项式的系数,从而可得出答案.
【详解】的系数是3,
故答案为:3.
【点睛】此题考查了单项式的知识,解答本题的关键是掌握单项式系数的定义.
2.(2022·湖南湘潭)下列整式与为同类项的是( )
A. B. C. D.
【答案】B
【解析】【分析】根据同类项的定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项,结合选项求解.
【详解】解:由同类项的定义可知,a的指数是1,b的指数是2.
A、a的指数是2,b的指数是1,与不是同类项,故选项不符合题意;
B、a的指数是1,b的指数是2,与是同类项,故选项符合题意;
C、a的指数是1,b的指数是1,与不是同类项,故选项不符合题意;
D、a的指数是1,b的指数是2,c的指数是1,与不是同类项,故选项不符合题意.故选:B.
【点睛】此题考查了同类项,判断同类项只要两看,即一看所含有的字母是否相同,二看相同字母的指数是否相同.
3.(2022·内蒙古包头)若一个多项式加上,结果得,则这个多项式为___________.
【答案】
【分析】设这个多项式为A,由题意得:,求解即可.
【详解】设这个多项式为A,由题意得:,
,
故答案为:.
【点睛】本题考查了整式的加减,准确理解题意,列出方程是解题的关键.
4.(2022·黑龙江大庆)已知代数式是一个完全平方式,则实数t的值为____________.
【答案】或
【分析】直接利用完全平方公式求解.
【详解】解:∵代数式是一个完全平方式,
∴,
∴,
解得或,
故答案为:或
【点睛】本题考查了完全平方公式的运用,熟记完全平方公式的特点是解题的关键.
题型三、整式的运算
1.(2022·江苏宿迁)下列运算正确的是( )
A. B. C. D.
【答案】C
【分析】由合并同类项可判断A,由同底数幂的乘法可判断B,由积的乘方运算可判断C,由幂的乘方运算可判断D,从而可得答案.
【详解】解:, 故A不符合题意;
, 故B不符合题意;
, 故C符合题意;
, 故D不符合题意;故选:C
【点睛】本题考查的是合并同类项,同底数幂的乘法,积的乘方运算,幂的乘方运算,掌握以上基础运算是解本题的关键.
2.(2022·四川眉山)下列运算中,正确的是( )
A. B.
C. D.
【答案】D
【分析】根据同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则分析选项即可知道答案.
【详解】解:A. ,根据同底数幂的乘法法则可知:,故选项计算错误,不符合题意;
B. ,和不是同类项,不能合并,故选项计算错误,不符合题意;
C. ,根据完全平方公式可得:,故选项计算错误,不符合题意;
D. ,根据单项式乘多项式的法则可知选项计算正确,符合题意;
故选:D
【点睛】本题考查同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则,解题的关键是掌握同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则.
3.(2022·浙江绍兴)下列计算正确的是( )
A. B. C. D.
【答案】A
【分析】根据多项式除以单项式、同底数幂的乘法、完全平方公式、幂的乘方法则逐项判断即可.
【详解】解:A、,原式计算正确;
B、,原式计算错误;
C、,原式计算错误;
D、,原式计算错误;故选:A.
【点睛】本题考查了多项式除以单项式、同底数幂的乘法、完全平方公式和幂的乘方,熟练掌握运算法则是解题的关键.
4.(2022·四川成都)下列计算正确的是( )
A. B. C. D.
【答案】D
【分析】根据合并同类项法则、单项式乘以多项式法则、完全平方公式及平方差公式进行运算,即可一一判定.
【详解】解:A.,故该选项错误,不符合题意;
B.,故该选项错误,不符合题意;
C.,故该选项错误,不符合题意;
D.,故该选项正确,符合题意;故选:D.
【点睛】本题考查了合并同类项法则、单项式乘以多项式法则、完全平方公式及平方差公式,熟练掌握和运用各运算法则和公式是解决本题的关键.
5.(2022·内蒙古包头)若,则m的值为( )
A.8 B.6 C.5 D.2
【答案】B
【分析】根据同底数幂的乘法运算计算,即可求解.
【详解】,
,故选:B.
【点睛】本题考查了同底数幂的乘法运算,即(m、n为正整数),熟练掌握运算法则是解题的关键.
题型四、因式分解及其应用
1.(2022·浙江嘉兴)分解因式:m2-1=_____.
【答案】
【分析】利用平方差公式进行因式分解即可.
【详解】解:m2-1= 故答案为:
【点睛】本题考查的是利用平方差公式分解因式,掌握“平方差公式的特点”是解本题的关键.
2.(2022·湖南怀化)因式分解:_____.
【答案】
【分析】根据提公因式法和平方差公式进行分解即可.
【详解】解:,
故答案为:
【点睛】本题考查了提公因式法和平方差公式,熟练掌握提公因式法和平方差公式是解题的关键.
3.(2022·浙江绍兴)分解因式: = ______.
【答案】
【分析】利用提公因式法即可分解.
【详解】,
故答案为:.
【点睛】本题考查了用提公因式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解.
4.(2022·浙江宁波)分解因式:x2-2x+1=__________.
【答案】(x-1)2
【详解】由完全平方公式可得:
故答案为.
【点睛】错因分析 容易题.失分原因是:①因式分解的方法掌握不熟练;②因式分解不彻底.
5.(2022·辽宁锦州)分解因式:____________.
【答案】
【分析】先提取公因数y,再利用完全平方公式进行二次分解.完全平方公式:(a±b)2=a2±2ab+b2.
【详解】解:;故答案为:
【点睛】本题考查了提公因式法分解因式和利用完全平方公式分解因式,难点在于需要进行二次分解因式.
6.(2022·江苏常州)分解因式:______.
【答案】xy(x+y)
【分析】利用提公因式法即可求解.
【详解】,故答案为:.
【点睛】本题考查了用提公因式法分解因式的知识,掌握提公因式法是解答本题的关键.
7.(2022·四川内江)分解因式:a4﹣3a2﹣4=_____.
【答案】(a2+1)(a+2)(a﹣2)
【分析】首先利用十字相乘法分解为 ,然后利用平方差公式进一步因式分解即可.
【详解】解:a4﹣3a2﹣4=(a2+1)(a2﹣4)=(a2+1)(a+2)(a﹣2),
故答案为:(a2+1)(a+2)(a﹣2).
【点睛】本题考查利用因式分解,解决问题的关键是掌握解题步骤:一提二套三检查.
8.(2022·湖北恩施)因式分解:=_______.
【答案】
【分析】先提公因式,再利用完全平方公式解题.
【详解】解:
故答案为:.
【点睛】本题考查因式分解,涉及提公因式、完全平方公式等知识,是重要考点,难度较易,掌握相关知识是解题关键.
9.(2022·山东临沂)因式分解=______.
【答案】.
【详解】解:
=
=,
故答案为.
10.(2022·四川乐山)已知,则______.
【答案】
【分析】根据已知式子,凑完全平方公式,根据非负数之和为0,分别求得的值,进而代入代数式即可求解.
【详解】解:,
,
即,
,
,
故答案为:.
【点睛】本题考查了因式分解的应用,掌握完全平方公式是解题的关键.
11.(2022·四川广安)已知a+b=1,则代数式a2﹣b2 +2b+9的值为________.
【答案】10
【分析】根据平方差公式,把原式化为,可得,即可求解.
【详解】解:a2﹣b2 +2b+9
故答案为:10
【点睛】本题主要考查了平方差公式的应用,利用整体代入思想解答是解题的关键.
题型五、乘法公式的应用
1.(2022·江苏苏州)已知,,则______.
【答案】24
【分析】根据平方差公式计算即可.
【详解】解:∵,,
∴,故答案为:24.
2.(2022·山东滨州)若,,则的值为_______.
【答案】90
【分析】将变形得到,再把,代入进行计算求解.
【详解】解:∵,,
∴ .故答案为:90.
【点睛】本题主要考查了代数式求值,完全平方公式的应用,灵活运用完全平方公式是解答关键.
3.(2022·四川德阳)已知(x+y)2=25,(x﹣y)2=9,则xy=___.
【答案】4
【分析】根据完全平方公式的运算即可.
【详解】∵,
∵+=4=16,∴=4.
【点睛】此题主要考查完全平方公式的灵活运用,解题的关键是熟知完全平方公式的应用.
4.(2022·广西)如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A. B.
C. D.
【答案】A
【分析】根据大正方形的面积=边长为a的正方形的面积+两个长为a,宽为b的长方形的面积+边长为b的正方形的面积,即可解答.
【详解】根据题意得:(a+b)2=a2+2ab+b2,故选:A.
【点睛】本题考查了完全平方公式的几何背景,用整体和部分两种方法表示面积是解题的关键.
题型六、整式的化简求值
1.(2022·湖南衡阳)先化简,再求值:,其中,.
【答案】,
【分析】利用平方差公式与多项式乘法法则进行化简,再代值计算.
【详解】解:原式,
将,代入式中得:
原式.
【点睛】本题考查多项式乘法与平方差公式,熟练掌握相关运算法则是解题的关键.
2.(2022·广西)先化简,再求值,其中.
【答案】x3-2xy+x,1
【分析】首先运用平方差公式计算,再运用单项式乘以多项式计算,最后合并同类项,即可化简,然后把x、y值代入计算即可.
【详解】解:
=x(x2-y2)+xy2-2xy+x
=x3-xy2+xy2-2xy+x
=x3-2xy+x,
当x=1,y=时,原式=13-2×1×+1=1.
【点睛】本题考查整式化简求值,熟练掌握整式混合运算法则是解题的关键.
3.(2022·北京)已知,求代数式的值.
【答案】5
【分析】先根据,得出,将变形为,最后代入求值即可.
【详解】解:∵,
∴,
∴
【点睛】本题主要考查了代数式求值,完全平方公式,单项式乘多项式,将变形为,是解题的关键.
4.(2022·吉林长春)先化简,再求值:,其中.
【答案】,
【分析】根据平方差公式与单项式乘以单项式进行计算,然后将代入求值即可求解.
【详解】解:原式=
当时,原式
【点睛】本题考查了整式的混合运算,实数的运算,代数式求值,正确的计算是解题的关键.
5.(2021·吉林长春)先化简,再求值:,其中.
【答案】
【解析】
【分析】
首先利用平方差公式,单项式乘以多项式去括号,再合并同类项,然后将a的值代入化简后的式子,即可解答本题.
【详解】
当时,
原式=.
【点睛】
本题考查了整式的混合运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.
题型七、数式的规律探究
1.(2022·云南)按一定规律排列的单项式:x,3x ,5x ,7x,9x,……,第n个单项式是( )
A.(2n-1) B.(2n+1) C.(n-1) D.(n+1)
【答案】A
【分析】系数的绝对值均为奇数,可用(2n-1)表示;字母和字母的指数可用xn表示.
【详解】解:依题意,得第n项为(2n-1)xn,故选:A.
【点睛】本题考查的是单项式,根据题意找出规律是解答此题的关键.
2.(2022·重庆)把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )
A.15 B.13 C.11 D.9
【答案】C
【分析】根据第①个图案中菱形的个数:;第②个图案中菱形的个数:;第③个图案中菱形的个数:;…第n个图案中菱形的个数:,算出第⑥个图案中菱形个数即可.
【详解】解:∵第①个图案中菱形的个数:;
第②个图案中菱形的个数:;
第③个图案中菱形的个数:;…
第n个图案中菱形的个数:,
∴则第⑥个图案中菱形的个数为:,故C正确.故选:C.
【点睛】本题主要考查的是图案的变化,解题的关键是根据已知图案归纳出图案个数的变化规律.
3.(2022·重庆)用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )
A.32 B.34 C.37 D.41
【答案】C
【分析】第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,由此可得:每增加1个图形,就会增加4个正方形,由此找到规律,列出第n个图形的算式,然后再解答即可.
【详解】解:第1个图中有5个正方形;
第2个图中有9个正方形,可以写成:5+4=5+4×1;
第3个图中有13个正方形,可以写成:5+4+4=5+4×2;
第4个图中有17个正方形,可以写成:5+4+4+4=5+4×3;...
第n个图中有正方形,可以写成:5+4(n-1)=4n+1;
当n=9时,代入4n+1得:4×9+1=37.故选:C.
【点睛】本题主要考查了图形的变化规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键.
4.(2022·黑龙江大庆)观察下列“蜂窝图”,按照这样的规律,则第16个图案中的“”的个数是____________.
【答案】49
【分析】根据题意可知:第1个图案中有六边形图形:1+2+1=4个,第2个图案中有六边形图形:2+3+2=7个,……由规侓即可得答案.
【详解】解:∵第1个图案中有六边形图形:1+2+1=4个,
第2个图案中有六边形图形:2+3+2=7个,
第3个图案中有六边形图形:3+4+3=10个,
第4个图案中有六边形图形:4+5+4=13个,
……
∴第16个图案中有六边形图形:16+17+16=49个,
故答案为:49.
【点睛】此题考查图形的变化规律,解题的关键是找出图形之间的运算规律,利用规律解决问题.
5.(2022·湖北恩施)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为,且满足.则________,________.
【答案】
【分析】由已知推出,得到,,,,上述式子相加求解即可.
【详解】解:∵;∴,
∵,
∵,
∴a4=,
∴,,,
把上述2022-1个式子相加得,
∴a2022=,
故答案为:,.
【点睛】此题主要考查数字的变化规律,关键是得出,利用裂项相加法求解.
模块一 数与式
专题2 整式与因式分解
整 式 的 相 关 概 念 单项式 由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数。如:单项式系数是,次数是4。
多项式 几个单项式的和叫做多项式;多项式中,每一个单项式叫做多项式的项,其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数。 如:多项式2+4x2y﹣是五次三项式
整式 整式是单项式与多项式的统称。
同类项 所含字母相同,并且相同字母的指数也分别相同的单项式叫做同类项。
合并同类项 把多项式中的同类项合并成一项叫做合并同类项,合并的法则是系数相加,所得的结果作为合并后的系数,字母和字母的指数不变。
整 式 运 算 幂的运算 同底数幂乘法 am·an=am+n(a≠0) am+n=am·an
同底数幂除法 =am-n(m,n是正整数) am-n=
幂的乘方 (am)n=amn(a≠0) amn=(am)n
积的乘方 (ab)n=anbn anbn=(ab)n
乘法 公式 平方差公式 (a+b)(a-b)=a2-b2 a2-b2=(a+b)(a-b)
完全平方公式 (a±b)2=a2±2ab+b2 a2±2ab+b2=(a±b)2
整式 加减 ① 整式的加减其实就是合并同类项; ② 整式加减的步骤:有括号,先去括号;有同类项,再合并同类项.注意去括号时,如果括号前面是负号,括号里各项的符号要变号.
整式 乘法 ① 单项式与单项式相乘:把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. ② 单项式与多项式相乘:m(a+b+c)=ma+mb+mC. ③ 多项式与多项式相乘:(m+n)(a+b)=ma+mb+na+nb.
整式 除法 ① 单项式除以单项式:把系数、同底数幂相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式. ② 多项式除以单项式:(a+b)÷m=a÷m+b÷m.
因式 分解 概念 把一个多项式化成几个整式积的形式,叫做多项式的因式分解。和的形式变积的形式
因式分解方法 提公因式法 ma+mb+mc=m(a+b+c)(乘法分配律的运用)
公式法 ① 运用平方差公式:a2-b2=(a+b)(a-b). ② 运用完全平方公式:a2±2ab+b2=(a±b)2.
求代数式的值 1.一般地,用数值代替代数式里的字母,按照代数式指明的运算关系计算出的结果就叫做代数式的值. 2.求代数式的值的基本步骤: ① 代入:一般情况下,先对代数式进行化简,再将数值代入; ② 计算:按代数式指明的运算关系计算出结果.
题型一、代数式及其求值
1.(2022·湖南邵阳)已知,则_________.
2.(2022·内蒙古赤峰)已知,则的值为( )
A.13 B.8 C.-3 D.5
3.(2022·湖南长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.元 B.元 C.元 D.元
题型二、整式的有关概念
1.(2022·广东)单项式的系数为___________.
2.(2022·湖南湘潭)下列整式与为同类项的是( )
A. B. C. D.
3.(2022·内蒙古包头)若一个多项式加上,结果得,则这个多项式为___________.
4.(2022·黑龙江大庆)已知代数式是一个完全平方式,则实数t的值为____________.
题型三、整式的运算
1.(2022·江苏宿迁)下列运算正确的是( )
A. B. C. D.
2.(2022·四川眉山)下列运算中,正确的是( )
A. B.
C. D.
3.(2022·浙江绍兴)下列计算正确的是( )
A. B. C. D.
4.(2022·四川成都)下列计算正确的是( )
A. B. C. D.
5.(2022·内蒙古包头)若,则m的值为( )
A.8 B.6 C.5 D.2
题型四、因式分解及其应用
1.(2022·浙江嘉兴)分解因式:m2-1=_____.
2.(2022·湖南怀化)因式分解:_____.
3.(2022·浙江绍兴)分解因式: = ______.
4.(2022·浙江宁波)分解因式:x2-2x+1=__________.
5.(2022·辽宁锦州)分解因式:____________.
6.(2022·江苏常州)分解因式:______.
7.(2022·四川内江)分解因式:a4﹣3a2﹣4=_____.
8.(2022·湖北恩施)因式分解:=_______.
9.(2022·山东临沂)因式分解=______.
10.(2022·四川乐山)已知,则______.
11.(2022·四川广安)已知a+b=1,则代数式a2﹣b2 +2b+9的值为________.
题型五、乘法公式的应用
1.(2022·江苏苏州)已知,,则______.
2.(2022·山东滨州)若,,则的值为_______.
3.(2022·四川德阳)已知(x+y)2=25,(x﹣y)2=9,则xy=___.
4.(2022·广西)如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A. B.
C. D.
题型六、整式的化简求值
1.(2022·湖南衡阳)先化简,再求值:,其中,.
2.(2022·广西)先化简,再求值,其中.
3.(2022·北京)已知,求代数式的值.
4.(2022·吉林长春)先化简,再求值:,其中.
5.(2021·吉林长春)先化简,再求值:,其中.
题型七、数式的规律探究
1.(2022·云南)按一定规律排列的单项式:x,3x ,5x ,7x,9x,……,第n个单项式是( )
A.(2n-1) B.(2n+1) C.(n-1) D.(n+1)
2.(2022·重庆)把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )
A.15 B.13 C.11 D.9
3.(2022·重庆)用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )
A.32 B.34 C.37 D.41
4.(2022·黑龙江大庆)观察下列“蜂窝图”,按照这样的规律,则第16个图案中的“”的个数是____________.
5.(2022·湖北恩施)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为,且满足.则________,________.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
2023年中考数学第一轮复习
模块一 数与式
专题2 整式与因式分解
知识梳理
整 式 的 相 关 概 念 单项式 由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数。 如:单项式系数是,次数是4。
多项式 几个单项式的和叫做多项式;多项式中,每一个单项式叫做多项式的项,其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数。 如:多项式2+4x2y﹣是五次三项式
整式 整式是单项式与多项式的统称。
同类项 所含字母相同,并且相同字母的指数也分别相同的单项式叫做同类项。
合并同类项 把多项式中的同类项合并成一项叫做合并同类项,合并的法则是系数相加,所得的结果作为合并后的系数,字母和字母的指数不变。
整 式 运 算 幂的运算 同底数幂乘法 am·an=am+n(a≠0) am+n=am·an
同底数幂除法 =am-n(m,n是正整数) am-n=
幂的乘方 (am)n=amn(a≠0) amn=(am)n
积的乘方 (ab)n=anbn anbn=(ab)n
乘法 公式 平方差公式 (a+b)(a-b)=a2-b2 a2-b2=(a+b)(a-b)
完全平方公式 (a±b)2=a2±2ab+b2 a2±2ab+b2=(a±b)2
整式 加减 ① 整式的加减其实就是合并同类项; ② 整式加减的步骤:有括号,先去括号;有同类项,再合并同类项.注意去括号时,如果括号前面是负号,括号里各项的符号要变号.
整式 乘法 ① 单项式与单项式相乘:把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. ② 单项式与多项式相乘:m(a+b+c)=ma+mb+mC. ③ 多项式与多项式相乘:(m+n)(a+b)=ma+mb+na+nb.
整式 除法 ① 单项式除以单项式:把系数、同底数幂相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式. ② 多项式除以单项式:(a+b)÷m=a÷m+b÷m.
因式 分解 概念 把一个多项式化成几个整式积的形式,叫做多项式的因式分解。和的形式变积的形式
因式分解方法 提公因式法 ma+mb+mc=m(a+b+c)(乘法分配律的运用)
公式法 ① 运用平方差公式:a2-b2=(a+b)(a-b). ② 运用完全平方公式:a2±2ab+b2=(a±b)2.
求代数式的值 1.一般地,用数值代替代数式里的字母,按照代数式指明的运算关系计算出的结果就叫做代数式的值. 2.求代数式的值的基本步骤: ① 代入:一般情况下,先对代数式进行化简,再将数值代入; ② 计算:按代数式指明的运算关系计算出结果.
题型梳理
题型一、代数式及其求值
1.(2022·湖南邵阳)已知,则_________.
【答案】2
【分析】将变形为即可计算出答案.
【详解】
∵
∴
故答案为:2.
【点睛】本题考查代数式的性质,解题的关键是熟练掌握代数式的相关知识.
2.(2022·内蒙古赤峰)已知,则的值为( )
A.13 B.8 C.-3 D.5
【答案】A
【分析】先化简已知的式子,再整体代入求值即可.
【详解】∵
∴
∴故选:A.
【点睛】本题考查平方差公式、代数式求值,利用整体思想是解题的关键.
3.(2022·湖南长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.元 B.元 C.元 D.元
【答案】C
【分析】根据题意列求得购买乙种读本本,根据单价乘以数量即可求解.
【详解】解:设购买甲种读本x本,则购买乙种读本本,乙种读本的单价为8元/本,则则购买乙种读本的费用为元故选C
【点睛】本题考查了列代数式,理解题意是解题的关键.
题型二、整式的有关概念
1.(2022·广东)单项式的系数为___________.
【答案】3
【分析】单项式中数字因数叫做单项式的系数,从而可得出答案.
【详解】的系数是3,
故答案为:3.
【点睛】此题考查了单项式的知识,解答本题的关键是掌握单项式系数的定义.
2.(2022·湖南湘潭)下列整式与为同类项的是( )
A. B. C. D.
【答案】B
【解析】【分析】根据同类项的定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项,结合选项求解.
【详解】解:由同类项的定义可知,a的指数是1,b的指数是2.
A、a的指数是2,b的指数是1,与不是同类项,故选项不符合题意;
B、a的指数是1,b的指数是2,与是同类项,故选项符合题意;
C、a的指数是1,b的指数是1,与不是同类项,故选项不符合题意;
D、a的指数是1,b的指数是2,c的指数是1,与不是同类项,故选项不符合题意.故选:B.
【点睛】此题考查了同类项,判断同类项只要两看,即一看所含有的字母是否相同,二看相同字母的指数是否相同.
3.(2022·内蒙古包头)若一个多项式加上,结果得,则这个多项式为___________.
【答案】
【分析】设这个多项式为A,由题意得:,求解即可.
【详解】设这个多项式为A,由题意得:,
,
故答案为:.
【点睛】本题考查了整式的加减,准确理解题意,列出方程是解题的关键.
4.(2022·黑龙江大庆)已知代数式是一个完全平方式,则实数t的值为____________.
【答案】或
【分析】直接利用完全平方公式求解.
【详解】解:∵代数式是一个完全平方式,
∴,
∴,
解得或,
故答案为:或
【点睛】本题考查了完全平方公式的运用,熟记完全平方公式的特点是解题的关键.
题型三、整式的运算
1.(2022·江苏宿迁)下列运算正确的是( )
A. B. C. D.
【答案】C
【分析】由合并同类项可判断A,由同底数幂的乘法可判断B,由积的乘方运算可判断C,由幂的乘方运算可判断D,从而可得答案.
【详解】解:, 故A不符合题意;
, 故B不符合题意;
, 故C符合题意;
, 故D不符合题意;故选:C
【点睛】本题考查的是合并同类项,同底数幂的乘法,积的乘方运算,幂的乘方运算,掌握以上基础运算是解本题的关键.
2.(2022·四川眉山)下列运算中,正确的是( )
A. B.
C. D.
【答案】D
【分析】根据同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则分析选项即可知道答案.
【详解】解:A. ,根据同底数幂的乘法法则可知:,故选项计算错误,不符合题意;
B. ,和不是同类项,不能合并,故选项计算错误,不符合题意;
C. ,根据完全平方公式可得:,故选项计算错误,不符合题意;
D. ,根据单项式乘多项式的法则可知选项计算正确,符合题意;
故选:D
【点睛】本题考查同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则,解题的关键是掌握同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则.
3.(2022·浙江绍兴)下列计算正确的是( )
A. B. C. D.
【答案】A
【分析】根据多项式除以单项式、同底数幂的乘法、完全平方公式、幂的乘方法则逐项判断即可.
【详解】解:A、,原式计算正确;
B、,原式计算错误;
C、,原式计算错误;
D、,原式计算错误;故选:A.
【点睛】本题考查了多项式除以单项式、同底数幂的乘法、完全平方公式和幂的乘方,熟练掌握运算法则是解题的关键.
4.(2022·四川成都)下列计算正确的是( )
A. B. C. D.
【答案】D
【分析】根据合并同类项法则、单项式乘以多项式法则、完全平方公式及平方差公式进行运算,即可一一判定.
【详解】解:A.,故该选项错误,不符合题意;
B.,故该选项错误,不符合题意;
C.,故该选项错误,不符合题意;
D.,故该选项正确,符合题意;故选:D.
【点睛】本题考查了合并同类项法则、单项式乘以多项式法则、完全平方公式及平方差公式,熟练掌握和运用各运算法则和公式是解决本题的关键.
5.(2022·内蒙古包头)若,则m的值为( )
A.8 B.6 C.5 D.2
【答案】B
【分析】根据同底数幂的乘法运算计算,即可求解.
【详解】,
,故选:B.
【点睛】本题考查了同底数幂的乘法运算,即(m、n为正整数),熟练掌握运算法则是解题的关键.
题型四、因式分解及其应用
1.(2022·浙江嘉兴)分解因式:m2-1=_____.
【答案】
【分析】利用平方差公式进行因式分解即可.
【详解】解:m2-1= 故答案为:
【点睛】本题考查的是利用平方差公式分解因式,掌握“平方差公式的特点”是解本题的关键.
2.(2022·湖南怀化)因式分解:_____.
【答案】
【分析】根据提公因式法和平方差公式进行分解即可.
【详解】解:,
故答案为:
【点睛】本题考查了提公因式法和平方差公式,熟练掌握提公因式法和平方差公式是解题的关键.
3.(2022·浙江绍兴)分解因式: = ______.
【答案】
【分析】利用提公因式法即可分解.
【详解】,
故答案为:.
【点睛】本题考查了用提公因式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解.
4.(2022·浙江宁波)分解因式:x2-2x+1=__________.
【答案】(x-1)2
【详解】由完全平方公式可得:
故答案为.
【点睛】错因分析 容易题.失分原因是:①因式分解的方法掌握不熟练;②因式分解不彻底.
5.(2022·辽宁锦州)分解因式:____________.
【答案】
【分析】先提取公因数y,再利用完全平方公式进行二次分解.完全平方公式:(a±b)2=a2±2ab+b2.
【详解】解:;故答案为:
【点睛】本题考查了提公因式法分解因式和利用完全平方公式分解因式,难点在于需要进行二次分解因式.
6.(2022·江苏常州)分解因式:______.
【答案】xy(x+y)
【分析】利用提公因式法即可求解.
【详解】,故答案为:.
【点睛】本题考查了用提公因式法分解因式的知识,掌握提公因式法是解答本题的关键.
7.(2022·四川内江)分解因式:a4﹣3a2﹣4=_____.
【答案】(a2+1)(a+2)(a﹣2)
【分析】首先利用十字相乘法分解为 ,然后利用平方差公式进一步因式分解即可.
【详解】解:a4﹣3a2﹣4=(a2+1)(a2﹣4)=(a2+1)(a+2)(a﹣2),
故答案为:(a2+1)(a+2)(a﹣2).
【点睛】本题考查利用因式分解,解决问题的关键是掌握解题步骤:一提二套三检查.
8.(2022·湖北恩施)因式分解:=_______.
【答案】
【分析】先提公因式,再利用完全平方公式解题.
【详解】解:
故答案为:.
【点睛】本题考查因式分解,涉及提公因式、完全平方公式等知识,是重要考点,难度较易,掌握相关知识是解题关键.
9.(2022·山东临沂)因式分解=______.
【答案】.
【详解】解:
=
=,
故答案为.
10.(2022·四川乐山)已知,则______.
【答案】
【分析】根据已知式子,凑完全平方公式,根据非负数之和为0,分别求得的值,进而代入代数式即可求解.
【详解】解:,
,
即,
,
,
故答案为:.
【点睛】本题考查了因式分解的应用,掌握完全平方公式是解题的关键.
11.(2022·四川广安)已知a+b=1,则代数式a2﹣b2 +2b+9的值为________.
【答案】10
【分析】根据平方差公式,把原式化为,可得,即可求解.
【详解】解:a2﹣b2 +2b+9
故答案为:10
【点睛】本题主要考查了平方差公式的应用,利用整体代入思想解答是解题的关键.
题型五、乘法公式的应用
1.(2022·江苏苏州)已知,,则______.
【答案】24
【分析】根据平方差公式计算即可.
【详解】解:∵,,
∴,故答案为:24.
2.(2022·山东滨州)若,,则的值为_______.
【答案】90
【分析】将变形得到,再把,代入进行计算求解.
【详解】解:∵,,
∴ .故答案为:90.
【点睛】本题主要考查了代数式求值,完全平方公式的应用,灵活运用完全平方公式是解答关键.
3.(2022·四川德阳)已知(x+y)2=25,(x﹣y)2=9,则xy=___.
【答案】4
【分析】根据完全平方公式的运算即可.
【详解】∵,
∵+=4=16,∴=4.
【点睛】此题主要考查完全平方公式的灵活运用,解题的关键是熟知完全平方公式的应用.
4.(2022·广西)如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A. B.
C. D.
【答案】A
【分析】根据大正方形的面积=边长为a的正方形的面积+两个长为a,宽为b的长方形的面积+边长为b的正方形的面积,即可解答.
【详解】根据题意得:(a+b)2=a2+2ab+b2,故选:A.
【点睛】本题考查了完全平方公式的几何背景,用整体和部分两种方法表示面积是解题的关键.
题型六、整式的化简求值
1.(2022·湖南衡阳)先化简,再求值:,其中,.
【答案】,
【分析】利用平方差公式与多项式乘法法则进行化简,再代值计算.
【详解】解:原式,
将,代入式中得:
原式.
【点睛】本题考查多项式乘法与平方差公式,熟练掌握相关运算法则是解题的关键.
2.(2022·广西)先化简,再求值,其中.
【答案】x3-2xy+x,1
【分析】首先运用平方差公式计算,再运用单项式乘以多项式计算,最后合并同类项,即可化简,然后把x、y值代入计算即可.
【详解】解:
=x(x2-y2)+xy2-2xy+x
=x3-xy2+xy2-2xy+x
=x3-2xy+x,
当x=1,y=时,原式=13-2×1×+1=1.
【点睛】本题考查整式化简求值,熟练掌握整式混合运算法则是解题的关键.
3.(2022·北京)已知,求代数式的值.
【答案】5
【分析】先根据,得出,将变形为,最后代入求值即可.
【详解】解:∵,
∴,
∴
【点睛】本题主要考查了代数式求值,完全平方公式,单项式乘多项式,将变形为,是解题的关键.
4.(2022·吉林长春)先化简,再求值:,其中.
【答案】,
【分析】根据平方差公式与单项式乘以单项式进行计算,然后将代入求值即可求解.
【详解】解:原式=
当时,原式
【点睛】本题考查了整式的混合运算,实数的运算,代数式求值,正确的计算是解题的关键.
5.(2021·吉林长春)先化简,再求值:,其中.
【答案】
【解析】
【分析】
首先利用平方差公式,单项式乘以多项式去括号,再合并同类项,然后将a的值代入化简后的式子,即可解答本题.
【详解】
当时,
原式=.
【点睛】
本题考查了整式的混合运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.
题型七、数式的规律探究
1.(2022·云南)按一定规律排列的单项式:x,3x ,5x ,7x,9x,……,第n个单项式是( )
A.(2n-1) B.(2n+1) C.(n-1) D.(n+1)
【答案】A
【分析】系数的绝对值均为奇数,可用(2n-1)表示;字母和字母的指数可用xn表示.
【详解】解:依题意,得第n项为(2n-1)xn,故选:A.
【点睛】本题考查的是单项式,根据题意找出规律是解答此题的关键.
2.(2022·重庆)把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )
A.15 B.13 C.11 D.9
【答案】C
【分析】根据第①个图案中菱形的个数:;第②个图案中菱形的个数:;第③个图案中菱形的个数:;…第n个图案中菱形的个数:,算出第⑥个图案中菱形个数即可.
【详解】解:∵第①个图案中菱形的个数:;
第②个图案中菱形的个数:;
第③个图案中菱形的个数:;…
第n个图案中菱形的个数:,
∴则第⑥个图案中菱形的个数为:,故C正确.故选:C.
【点睛】本题主要考查的是图案的变化,解题的关键是根据已知图案归纳出图案个数的变化规律.
3.(2022·重庆)用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )
A.32 B.34 C.37 D.41
【答案】C
【分析】第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,由此可得:每增加1个图形,就会增加4个正方形,由此找到规律,列出第n个图形的算式,然后再解答即可.
【详解】解:第1个图中有5个正方形;
第2个图中有9个正方形,可以写成:5+4=5+4×1;
第3个图中有13个正方形,可以写成:5+4+4=5+4×2;
第4个图中有17个正方形,可以写成:5+4+4+4=5+4×3;...
第n个图中有正方形,可以写成:5+4(n-1)=4n+1;
当n=9时,代入4n+1得:4×9+1=37.故选:C.
【点睛】本题主要考查了图形的变化规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键.
4.(2022·黑龙江大庆)观察下列“蜂窝图”,按照这样的规律,则第16个图案中的“”的个数是____________.
【答案】49
【分析】根据题意可知:第1个图案中有六边形图形:1+2+1=4个,第2个图案中有六边形图形:2+3+2=7个,……由规侓即可得答案.
【详解】解:∵第1个图案中有六边形图形:1+2+1=4个,
第2个图案中有六边形图形:2+3+2=7个,
第3个图案中有六边形图形:3+4+3=10个,
第4个图案中有六边形图形:4+5+4=13个,
……
∴第16个图案中有六边形图形:16+17+16=49个,
故答案为:49.
【点睛】此题考查图形的变化规律,解题的关键是找出图形之间的运算规律,利用规律解决问题.
5.(2022·湖北恩施)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为,且满足.则________,________.
【答案】
【分析】由已知推出,得到,,,,上述式子相加求解即可.
【详解】解:∵;∴,
∵,
∵,
∴a4=,
∴,,,
把上述2022-1个式子相加得,
∴a2022=,
故答案为:,.
【点睛】此题主要考查数字的变化规律,关键是得出,利用裂项相加法求解.
同课章节目录
