【模块三 函数】专题1 平面直角坐标系和函数的概念-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块三 函数】专题1 平面直角坐标系和函数的概念-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 14:54:35 | ||
图片预览



文档简介
2023年中考数学第一轮复习
模块三 函数
专题1 平面直角坐标系和函数的概念
直角坐标系 平面直角坐标系 (1)对应关系:坐标平面内的点与有序实数对是一一对应的. (2)坐标轴上的点:x轴,y轴上的点不属于任何象限.
点的坐标特征 各象限内点的坐标特征:
坐标轴上点的特征: x轴上点的纵坐标为0; y轴上点的横坐标为0; 原点的坐标为(0,0).
对称点的坐标特征: 点P(x,y)关于x轴的对称点为P1(x,-y); 点P(x,y)关于y轴的对称点为P2(-x,y); 点P(x,y)关于原点的对称点为P3(-x,-y).
点的平移特征: 将点P(x,y)向右(或左)平移a个单位长度后得P'(x+a,y)(或P'(x-a,y)); 将点P(x,y)向上(或下)平移b个单位长度后得P″(x,y+b)(或P″(x,y-b)).
点到坐标轴的距离: 点P(x,y)到x轴的距离为|y|;到y轴的距离为|x|.
函数的认识 函数的有关概念 变量与常量: 在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
函数的概念: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
表示方法: 解析式法、列表法、图象法.
自变量的 取值范围 ① 解析式是整式时,自变量的取值范围是全体实数; ② 解析式是分式时,自变量的取值范围是分母不为0的实数; ③ 解析式是二次根式时,自变量的取值范围是被开方数大于等于0;
函数值: 对于一个函数,如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
函数的图象 函数图象的概念: 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数图象的画法: 列表、描点、连线.
题型一、平面直角坐标系的点的特征
1.(2022·四川乐山)点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022·湖南长沙)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
3.(2022·广东)在平面直角坐标系中,将点向右平移2个单位后,得到的点的坐标是( )
A. B. C. D.
4.(2022·四川雅安)在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为( )
A.﹣4 B.4 C.12 D.﹣12
5.(2022·江苏扬州)在平面直角坐标系中,点P(﹣3,a2+1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022·贵州铜仁)如图,在矩形中,,则D的坐标为( )
A. B. C. D.
7.(2022·四川广安)若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第________象限.
题型二、函数的相关概念及图象
1.(2022·广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为.下列判断正确的是( )
A.2是变量 B.是变量 C.r是变量 D.C是常量
2.(2022·上海)已知f(x)=3x,则f(1)=_____.
3.(2022·黑龙江大庆)在函数中,自变量的取值范围是_________.
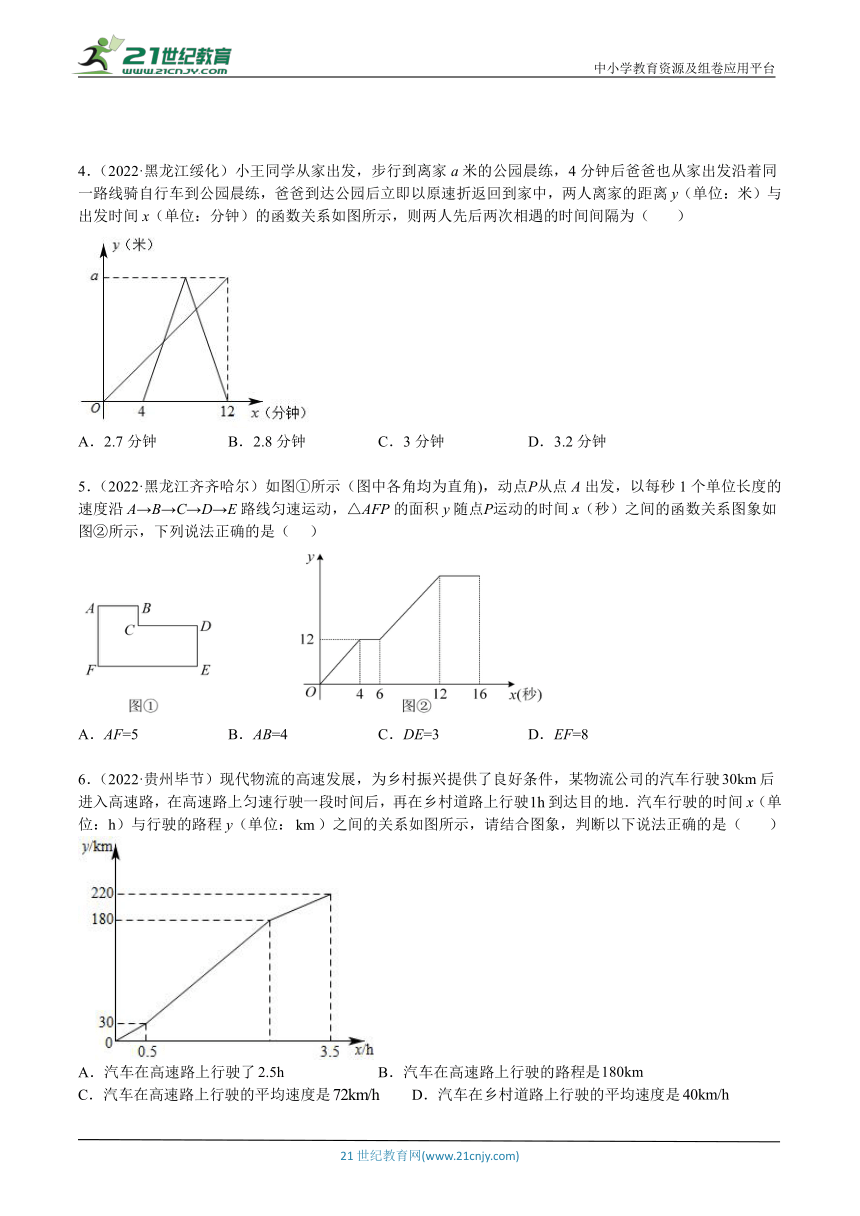
4.(2022·黑龙江绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
5.(2022·黑龙江齐齐哈尔)如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )
A.AF=5 B.AB=4 C.DE=3 D.EF=8
6.(2022·贵州毕节)现代物流的高速发展,为乡村振兴提供了良好条件,某物流公司的汽车行驶后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶到达目的地.汽车行驶的时间x(单位:h)与行驶的路程y(单位:)之间的关系如图所示,请结合图象,判断以下说法正确的是( )
A.汽车在高速路上行驶了 B.汽车在高速路上行驶的路程是
C.汽车在高速路上行驶的平均速度是 D.汽车在乡村道路上行驶的平均速度是
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
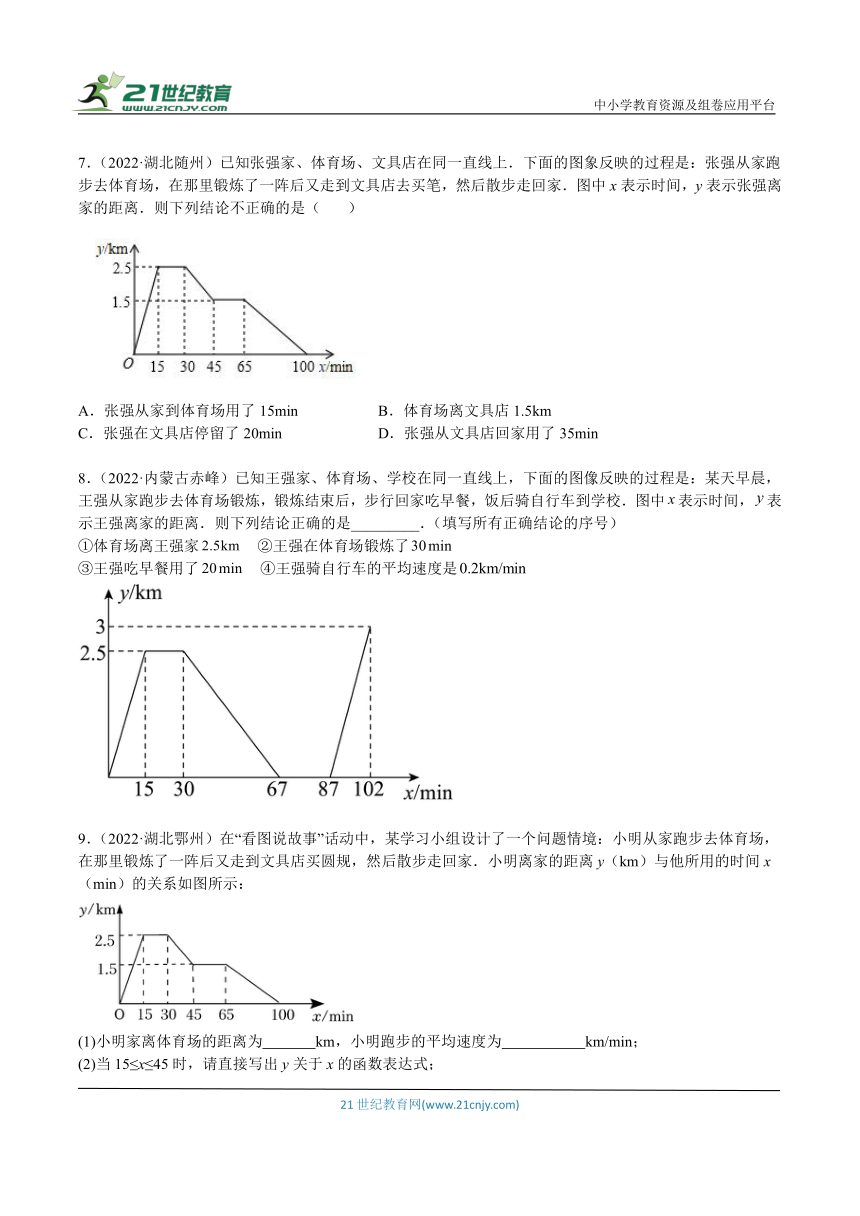
7.(2022·湖北随州)已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
A.张强从家到体育场用了15min B.体育场离文具店1.5km
C.张强在文具店停留了20min D.张强从文具店回家用了35min
8.(2022·内蒙古赤峰)已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是_________.(填写所有正确结论的序号)
①体育场离王强家 ②王强在体育场锻炼了
③王强吃早餐用了 ④王强骑自行车的平均速度是
9.(2022·湖北鄂州)在“看图说故事”话动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)小明家离体育场的距离为 km,小明跑步的平均速度为 km/min;
(2)当15≤x≤45时,请直接写出y关于x的函数表达式;
(3)当小明离家2km时,求他离开家所用的时间.
10.(2022·黑龙江齐齐哈尔)在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y (米)与出发时间x (分钟)之间的函数关系如图所示,请结合图像解答下列问题:
(1)A、B两地之间的距离是 米,乙的步行速度是 米/分;
(2)图中a= ,b= ,c= ;
(3)求线段MN的函数解析式;
(4)在乙运动的过程中,何时两人相距80米 (直接写出答案即可)
11.(2022·黑龙江)为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)甲车速度是_______km/h,乙车出发时速度是_______km/h;
(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);
(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.
题型三、动点问题的函数图像判断
1.(2022·甘肃武威)如图1,在菱形中,,动点从点出发,沿折线方向匀速运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2所示,则的长为( )
A. B. C. D.
2.(2022·辽宁)如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A.B.C.D.
3.如图,在 中,,,,点 E 在 边上由点 A 向点 B 运动(不与点 A,点 B 重合),过点E 作 垂直 交直角边于 F.设, 面积为 y,则 y 关于 x 的函数图象大致是( )
A.B.C. D.
4.如图,点是菱形的对角线上的一个动点,过点垂直于的直线交菱形的边于、两点.设,,,的面积为y,则y关于x的函数图象大致形状是( )
A.B.C. D.
5.(2021·新疆)如图,在矩形ABCD中,,.点P从点A出发,以2cm/s的速度在矩形的边上沿运动,当点P与点D重合时停止运动.设运动的时间为(单位:s),的面积为S(单位:),则S随t变化的函数图象大致为( )
A. B.
C. D.
6.如图,在菱形ABCD中,其边长为4cm,,垂直于AD的直线EF(直线EF与菱形ABCD的两边分别交于点E,F,且点E在点F的上方)从点A出发,沿AD方向以每秒1cm的速度向右平移.若的面积为,直线EF的运动时间为,则下列能大致反映y与x的函数关系的图象是( )
A. B.C. D.
7.(2022·山东潍坊)如图,在 ABCD中,∠A=60°,AB=2,AD=1,点E,F在 ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A. B.
C. D.
8.(2022·辽宁)如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
题型四、平面直角坐标系的规律探究
1.(2022 河南)如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2 022次旋转结束时,点A的坐标为( )
A.(,-1) B.(-1,-) C.(-,-1) D.(1,)
2.(2022·黑龙江齐齐哈尔)如图,直线与轴相交于点,与轴相交于点,过点作交轴于点,过点作轴交于点,过点作交轴于点,过点作轴交于点…,按照如此规律操作下去,则点的纵坐标是______.
3.(2021·贵州毕节)如图,在平面直角坐标系中,点在直线上,过点作,交轴于点;过点作轴,交直线于点;过点作,交轴于点;过点作轴,交直线于点;…;按此作法进行下去,则点的坐标为_____________.
4.(2021·内蒙古呼伦贝尔)如图,点在直线上,点的横坐标为1,过点作轴,垂足为,以为边向右作正方形,延长交直线l于点;以为边向右作正方形,延长交直线l于点;……;按照这个规律进行下去,点的坐标为___________.
5.(2022·黑龙江)如图,在平面直角坐标系中,点,,,……在x轴上且,,,……按此规律,过点,,,……作x轴的垂线分别与直线交于点,,,……记,,,……的面积分别为,,,……,则______.
6.(2022·贵州毕节)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为_________.
2023年中考数学第一轮复习
模块三 函数
专题1 平面直角坐标系和函数的概念
知识梳理
直角坐标系 平面直角坐标系 (1)对应关系:坐标平面内的点与有序实数对是一一对应的. (2)坐标轴上的点:x轴,y轴上的点不属于任何象限.
点的坐标特征 各象限内点的坐标特征:
坐标轴上点的特征: x轴上点的纵坐标为0; y轴上点的横坐标为0; 原点的坐标为(0,0).
对称点的坐标特征: 点P(x,y)关于x轴的对称点为P1(x,-y); 点P(x,y)关于y轴的对称点为P2(-x,y); 点P(x,y)关于原点的对称点为P3(-x,-y).
点的平移特征: 将点P(x,y)向右(或左)平移a个单位长度后得P'(x+a,y)(或P'(x-a,y)); 将点P(x,y)向上(或下)平移b个单位长度后得P″(x,y+b)(或P″(x,y-b)).
点到坐标轴的距离: 点P(x,y)到x轴的距离为|y|;到y轴的距离为|x|.
函数的认识 函数的有关概念 变量与常量: 在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
函数的概念: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
表示方法: 解析式法、列表法、图象法.
自变量的 取值范围 ① 解析式是整式时,自变量的取值范围是全体实数; ② 解析式是分式时,自变量的取值范围是分母不为0的实数; ③ 解析式是二次根式时,自变量的取值范围是被开方数大于等于0;
函数值: 对于一个函数,如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
函数的图象 函数图象的概念: 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数图象的画法: 列表、描点、连线.
题型梳理
题型一、平面直角坐标系的点的特征
1.(2022·四川乐山)点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】根据各象限内点的坐标特征解答即可.
【详解】解:点( 1,2)所在的象限是第二象限.故选:B.
2.(2022·湖南长沙)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
【答案】D
【分析】根据关于原点对称的两个点,横坐标、纵坐标分别互为相反数,即可求解.
【详解】解:点关于原点对称的点的坐标是.故选D.
3.(2022·广东)在平面直角坐标系中,将点向右平移2个单位后,得到的点的坐标是( )
A. B. C. D.
【答案】A
【分析】把点的横坐标加2,纵坐标不变,得到,就是平移后的对应点的坐标.
【详解】解:点向右平移2个单位长度后得到的点的坐标为.
故选A.
4.(2022·四川雅安)在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为( )
A.﹣4 B.4 C.12 D.﹣12
【答案】D
【分析】首先根据关于原点对称的点的坐标特点可得,可得a,b的值,再代入求解即可得到答案.
【详解】解: 点(a+2,2)关于原点的对称点为(4,﹣b),
,
解得:
故选D
5.(2022·江苏扬州)在平面直角坐标系中,点P(﹣3,a2+1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【详解】∵a2 0,∴a2+1 1,∴点P( 3,a2+1)所在的象限是第二象限.故选B.
6.(2022·贵州铜仁)如图,在矩形中,,则D的坐标为( )
A. B. C. D.
【答案】D
【分析】先根据A、B的坐标求出AB的长,则CD=AB=6,并证明轴,同理可得轴,由此即可得到答案.
【详解】解:∵A(-3,2),B(3,2),
∴AB=6,轴,
∵四边形ABCD是矩形,
∴CD=AB=6,轴,
同理可得轴,
∵点C(3,-1),
∴点D的坐标为(-3,-1),
故选D.
7.(2022·四川广安)若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第________象限.
【答案】二
【分析】根据点P(m+1,m)在第四象限,可得到,从而得到,即可求解.
【详解】解:∵点P(m+1,m)在第四象限,
∴,解得:,
∴,
∴点Q(﹣3,m+2)在第二象限.
故答案为:二
题型二、函数的相关概念及图象
1.(2022·广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为.下列判断正确的是( )
A.2是变量 B.是变量 C.r是变量 D.C是常量
【答案】C
【分析】根据变量与常量的定义分别判断,并选择正确的选项即可.
【详解】解:2与π为常量,C与r为变量,
故选C.
2.(2022·上海)已知f(x)=3x,则f(1)=_____.
【答案】3
【分析】直接代入求值即可.
【详解】解:∵f(x)=3x,∴f(1)=3×1=3,故答案为:3
3.(2022·黑龙江大庆)在函数中,自变量的取值范围是_________.
【答案】
【分析】二次根式内非负,则函数有意义.
【详解】要使函数有意义,则二次根式内为非负
∴2x+3≥0
解得:
故答案为:
4.(2022·黑龙江绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
【答案】C
【分析】先根据题意求得A、D、E、F的坐标,然后再运用待定系数法分别确定AE、AF、OD的解析式,再分别联立OD与AE和AF求得两次相遇的时间,最后作差即可.
【详解】解: 如图:根据题意可得A(8,a),D(12,a),E(4,0),F(12,0)
设AE的解析式为y=kx+b,则 ,解得
∴直线AE的解析式为y=x-3a
同理:直线AF的解析式为:y=-x+3a,直线OD的解析式为:y=
联立 ,解得
联立 ,解得
两人先后两次相遇的时间间隔为9-6=3min.
故答案为C.
5.(2022·黑龙江齐齐哈尔)如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )
A.AF=5 B.AB=4 C.DE=3 D.EF=8
【答案】B
【分析】路线为A→B→C→D→E,将每段路线在坐标系中对应清楚即可得出结论.
【详解】解:坐标系中对应点运动到B点
B选项正确
即:
解得:
A选项错误
12~16s对应的DE段
C选项错误
6~12s对应的CD段
D选项错误故选:B.
6.(2022·贵州毕节)现代物流的高速发展,为乡村振兴提供了良好条件,某物流公司的汽车行驶后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶到达目的地.汽车行驶的时间x(单位:h)与行驶的路程y(单位:)之间的关系如图所示,请结合图象,判断以下说法正确的是( )
A.汽车在高速路上行驶了 B.汽车在高速路上行驶的路程是
C.汽车在高速路上行驶的平均速度是 D.汽车在乡村道路上行驶的平均速度是
【答案】D
【分析】观察图象可得汽车在高速路上行驶了3.5-0.5-1=2h;汽车在高速路上行驶的路程是180-30=150km;汽车在高速路上行驶的平均速度是150÷2=75km/h;汽车在乡村道路上行驶的平均速度是(220-180)÷1=40km/h,即可求解.
【详解】解:A、根据题意得:汽车在高速路上行驶了3.5-0.5-1=2h,故本选项错误,不符合题意;
B、汽车在高速路上行驶的路程是180-30=150km,故本选项错误,不符合题意;
C、汽车在高速路上行驶的平均速度是150÷2=75km/h,故本选项错误,不符合题意;
D、汽车在乡村道路上行驶的平均速度是(220-180)÷1=40km/h,故本选项正确,符合题意;选:D
7.(2022·湖北随州)已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
A.张强从家到体育场用了15min B.体育场离文具店1.5km
C.张强在文具店停留了20min D.张强从文具店回家用了35min
【答案】B
【分析】利用图象信息解决问题即可.
【详解】解:由图可知:
A. 张强从家到体育场用了15min,正确,不符合题意;
B. 体育场离文具店的距离为:,故选项错误,符合题意;
C. 张强在文具店停留了:,正确,不符合题意;
D. 张强从文具店回家用了,正确,符合题意,
故选:B.
8.(2022·内蒙古赤峰)已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是_________.(填写所有正确结论的序号)
①体育场离王强家 ②王强在体育场锻炼了
③王强吃早餐用了 ④王强骑自行车的平均速度是
【答案】①③④
【分析】利用图象信息解决问题即可.
【详解】解:体育场离张强家,①正确;
王强在体育场锻炼了,②错误;
王强吃早餐用了,③正确;
王强骑自行车的平均速度是,④正确.
故答案为:①③④.
9.(2022·湖北鄂州)在“看图说故事”话动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)小明家离体育场的距离为 km,小明跑步的平均速度为 km/min;
(2)当15≤x≤45时,请直接写出y关于x的函数表达式;
(3)当小明离家2km时,求他离开家所用的时间.
【答案】(1)2.5;;
(2)
(3)当小明离家2km时,他离开家所用的时间为12min或37.5min
【分析】(1)根据函数图象结合路程=时间×速度进行求解即可;
(2)分当时和当时两种情况讨论求解即可;
(3)分当小明处在去体育馆的途中离家2km时,当小明从体育馆去商店途中离家2kn时两种情况讨论求解即可.
(1)
解:由函数图象可知小明在离家15分钟时到底体育馆,此时离家的距离为2.5km,
∴小明家离体育馆的距离为2.5km,小明跑步的平均速度为,
故答案为:2.5;;
(2)
解:由函数图象可知当时,,
当时,此时y是关于x一次函数,设,
∴,
解得,
∴此时,
综上所述,
(3)
解:当小明处在去体育馆的途中离家2km时,
;
当小明从体育馆去商店途中离家2km时,
∴,
解得;
综上所述,当小明离家2km时,他离开家所用的时间为12min或37.5min.
10.(2022·黑龙江齐齐哈尔)在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y (米)与出发时间x (分钟)之间的函数关系如图所示,请结合图像解答下列问题:
(1)A、B两地之间的距离是 米,乙的步行速度是 米/分;
(2)图中a= ,b= ,c= ;
(3)求线段MN的函数解析式;
(4)在乙运动的过程中,何时两人相距80米 (直接写出答案即可)
【答案】(1)1200,60
(2)900,800,15
(3)y =-20x+1200(15≤x≤20)
(4)8分钟,分钟
【分析】(1)分析图像,出发前两人之间的距离即为A、B两地之间的距离,为1200米,乙经过20分钟时到达A地,所以乙的速度为可计算出来;
(2)由函数图像可知,经过分钟时两人相遇,则可算出甲的速度,经过c分钟时两人距离重新达到最大,此时甲到达B地,则可求出a,经过20分钟时乙到达A地,此时两人相距b米,利用甲乙的速度即可算出b;
(3)由(2)可知M、N的坐标,设出MN的一般解析式,将M、N的坐标代入即可求出;
(4)设经过x分钟两人相距80米,根据两人相遇前和相遇后都可相距80米分别列方程即可求出.
(1)
由函数图像可知,最开始时甲乙两人之间的距离为1200米,
因为甲从A地出发,乙从B地出发,两人最开始时的距离就是A、B两地之间的距离,
所以A、B两地之间距离为1200米;
由图像可知乙经过20分时到达A地,
∴乙的步行速度为(米/分);
故答案为:1200,60;
(2)
由函数图像可知,经过分钟时两人相遇,经过c分钟时两人距离重新达到最大,此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,
设甲的步行速度为x米/分,则,
解得:x=80(米/分)
∴(分),
(米),
(米).
故答案为:900,800,15;
(3)
由(2)可知,M、N的坐标分别为M(15,900),N(20,800),
设线段MN的解析式为y=kx+b(),
则有 ,
解得:
∴线段MN的函数解析式是y =-20x+1200(15≤x≤20)
(4)
设经过x分钟两人相距80米,两人相遇前和相遇后都可相距80米,
相遇前:1200-(60+80)x=80,解得:x=8;
相遇后:(60+80)x-1200=80,解得:x=,
所以经过8分钟和分钟时两人相距80米.
11.(2022·黑龙江)为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)甲车速度是_______km/h,乙车出发时速度是_______km/h;
(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);
(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.
【答案】(1)100 60
(2)
(3)3,6.3,9.125
【分析】(1)根据图象分别得出甲车5h的路程为500km,乙车5h的路程为300km,即可确定各自的速度;
(2)设,由图象可得经过点(9,300),(12,0)点,利用待定系数法即可确定函数解析式;
(3)乙出发的时间为t时,相距120km,根据图象分多个时间段进行分析,利用速度与路程、时间的关系求解即可.
(1)
解:根据图象可得,甲车5h的路程为500km,
∴甲的速度为:500÷5=100km/h;
乙车5h的路程为300km,
∴乙的速度为:300÷5=60km/h;
故答案为:100;60;
(2)
设,由图象可得经过点(9,300),(12,0)点,
代入得,
解得
∴y与x的函数解析式为;
(3)
解:设乙出发的时间为t时,相距120km,
根据图象可得,
当0100t-60t=120,
解得:t=3;
当5当5.5500-100(t-5.5)-300=120,
解得:t=6.3;
当8100(t-8)-300=120,
解得:t=12.2,不符合题意,舍去;
当9100×(9-8)+100(t-9)+60(t-9)=120,
解得:t=9.125;
综上可得:乙车出发3h、6.3h与9.125h时,两车之间的距离为120km.
题型三、动点问题的函数图像判断
1.(2022·甘肃武威)如图1,在菱形中,,动点从点出发,沿折线方向匀速运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2所示,则的长为( )
A. B. C. D.
【答案】B
【分析】根据图1和图2判定三角形ABD为等边三角形,它的面积为解答即可.
【详解】解:在菱形ABCD中,∠A=60°,
∴△ABD为等边三角形, 设AB=a,由图2可知,△ABD的面积为,
∴△ABD的面积 解得:a= 故选B
2.(2022·辽宁)如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A.B.C.D.
【答案】A
【分析】分三种情形∶ ①当0<x≤2时, 重叠部分为△CDG,②当2<x≤4时,重叠部分为四边形AGDC,③当4<x≤8时,重叠部分为△BEG,分别计算即可.
【详解】解:过点A作AM⊥BC,交BC于点M,
在等边△ABC中,∠ACB=60°,
在Rt△DEF中,∠F=30°,
∴∠FED=60°,
∴∠ACB=∠FED,
∴ACEF,
在等边△ABC中,AM⊥BC,
∴BM=CM=BC=2,AM=BM=2,
∴S△ABC=BC AM=4,
①当0<x≤2时,设AC与DF交于点G,此时△ABC与Rt△DEF重叠部分为△CDG,
由题意可得CD=x,DG=x
∴S=CD DG=x2;
②当2<x≤4时,设AB与DF交于点G,此时△ABC与Rt△DEF重叠部分为四边形AGDC,
由题意可得:CD=x,则BD=4﹣x,DG=(4﹣x),
∴S=S△ABC﹣S△BDG=4﹣×(4﹣x)×(4﹣x),
∴S=﹣x2+4x﹣4=﹣(x﹣4)2+4,
③当4<x≤8时,设AB与EF交于点G,过点G作GM⊥BC,交BC于点M,
此时△ABC与Rt△DEF重叠部分为△BEG,
由题意可得CD=x,则CE=x﹣4,DB=x﹣4,
∴BE=x﹣(x﹣4)﹣(x﹣4)=8﹣x,
∴BM=4﹣x
在Rt△BGM中,GM=(4﹣x),
∴S=BE GM=(8﹣x)×(4﹣x),
∴S=(x﹣8)2,
综上,选项A的图像符合题意,
故选:A.
3.如图,在 中,,,,点 E 在 边上由点 A 向点 B 运动(不与点 A,点 B 重合),过点E 作 垂直 交直角边于 F.设, 面积为 y,则 y 关于 x 的函数图象大致是( )
A.B.C. D.
【答案】D
【分析】过点作于点,利用勾股定理以及面积法求得的长,分和两种情况讨论,利用相似三角形的判定和性质求解即可;
【详解】解:过点作于点,
,
,
,
,
当,
,
,
,
,即,
,
,开口向上的一段抛物线;
当,
同理可证,
,即,
,
,开口向下的一段抛物线;
综上,符合题意的函数关系的图象是D;
故选:D.
4.如图,点是菱形的对角线上的一个动点,过点垂直于的直线交菱形的边于、两点.设,,,的面积为y,则y关于x的函数图象大致形状是( )
A.B.C. D.
【答案】A
【分析】的面积,通过题干已知条件,用分别表示出、,根据所得的函数,利用其图象,可分两种情况解答:①;②.
【详解】解:①当时,如图1,
在菱形中,,,,且;
,
∴
,
,
即,
,
,
,
函数图象开口向下;
②当,如图2,
同理证得,,
,
即,
,
,
,
函数图象开口向上;
综上,答案A的图象大致符合;
故选:A.
5.(2021·新疆)如图,在矩形ABCD中,,.点P从点A出发,以2cm/s的速度在矩形的边上沿运动,当点P与点D重合时停止运动.设运动的时间为(单位:s),的面积为S(单位:),则S随t变化的函数图象大致为( )
A. B. C. D.
【答案】D
【解析】
【分析】
分点P在AB上运动, 0≤t≤4;点P在BC上运动, 4<t≤7;点P在CD上运动, 7<t≤11,分别计算即可
【详解】
当点P在AB上运动时, S==6t,0≤t≤4;
当点P在BC上运动时, S==24,4<t≤7;
点P在CD上运动, S=, 7<t≤11,
故选D.
6.如图,在菱形ABCD中,其边长为4cm,,垂直于AD的直线EF(直线EF与菱形ABCD的两边分别交于点E,F,且点E在点F的上方)从点A出发,沿AD方向以每秒1cm的速度向右平移.若的面积为,直线EF的运动时间为,则下列能大致反映y与x的函数关系的图象是( )
A. B.
C. D.
【答案】D
【分析】根据,分别求出EF的长度代入即可判断函数图象.
【详解】解:∵四边形ABCD是菱形,边长为4,∠A=60°,
∴当E、B重合时,AF=2,
当,,,
∴,
即,
∴y与x的函数是开口向上的二次函数,图象为抛物线的一部分;
当,EF为常数=,
∴,
即,
∴y与x是正比例函数,图象为直线的一部分,
故选:D.
7.(2022·山东潍坊)如图,在 ABCD中,∠A=60°,AB=2,AD=1,点E,F在 ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A. B. C. D.
【答案】A
【分析】分0≤x≤1,1【详解】解:当0≤x≤1时,过点F作FG⊥AB于点G,
∵∠A=60°,AE=AF=x,
∴AG=x,
由勾股定理得FG=x,
∴y=AE×FG=x2,图象是一段开口向上的抛物线;
当1∵∠DAH=60°,AE=x,AD=1,DF= x-1,
∴AH=,
由勾股定理得DH=,
∴y=(DF+AE)×DH=x-,图象是一条线段;
当2≤x≤3时,过点E作EI⊥CD于点I,
∵∠C=∠DAB=60°,CE=CF=3-x,
同理求得EI=(3-x),
∴y= AB×DH -CF×EI=-(3-x)2=-x2+x-,图象是一段开口向下的抛物线;
观察四个选项,只有选项A符合题意,故选:A.
【点睛】本题考查了利用分类讨论的思想求动点问题的函数图象;也考查了平行四边形的性质,含30度的直角三角形的性质,勾股定理,三角形的面积公式以及一次函数和二次函数的图象.
8.(2022·辽宁)如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
【答案】D
【分析】由题意易得,,则有,进而可分当点P在AB中点的左侧时和在AB中点的右侧时,然后分类求解即可.
【详解】解:∵,
∴,由题意知:,∴,
由折叠的性质可得:,
当点P与AB中点重合时,则有,
当点P在AB中点的左侧时,即,
∴与重叠部分的面积为;
当点P在AB中点的右侧时,即,如图所示:
由折叠性质可得:,,
∴,∴,∴,
∴与重叠部分的面积为;
综上所述:能反映与重叠部分的面积S与t之间函数关系的图象只有D选项;故选D.
题型四、平面直角坐标系的规律探究
1.(2022 河南)如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2 022次旋转结束时,点A的坐标为( )
A.(,-1) B.(-1,-) C.(-,-1) D.(1,)
2.(2022·黑龙江齐齐哈尔)如图,直线与轴相交于点,与轴相交于点,过点作交轴于点,过点作轴交于点,过点作交轴于点,过点作轴交于点…,按照如此规律操作下去,则点的纵坐标是______.
【答案】
【分析】先根据30°的特殊直角三角形,如,,,求出B点,B1点的纵坐标,发现规律,即可
【详解】∵
当时,
当时,
故,
∴为30°的直角三角形
∴
∵
∴为30°的直角三角形
∴
∴为30°的直角三角形
∵轴
∴
∴
为30°的直角三角形
同理:
…
故:
故答案为:
3.(2021·贵州毕节)如图,在平面直角坐标系中,点在直线上,过点作,交轴于点;过点作轴,交直线于点;过点作,交轴于点;过点作轴,交直线于点;…;按此作法进行下去,则点的坐标为_____________.
【答案】(,0).
【解析】
【分析】
根据题目所给的解析式,求出对应的坐标,然后根据规律求出的坐标,最后根据题目要求求出最后答案即可.
【详解】
解:如图,过点N作NM⊥x轴于M
将代入直线解析式中得
∴,45°
∵90°
∴
∵
∴
∴的坐标为(2,0)
同理可以求出的坐标为(4,0)
同理可以求出的坐标为(8,0)
同理可以求出的坐标为(,0)
∴的坐标为(,0)
故答案为:(,0).
4.(2021·内蒙古呼伦贝尔)如图,点在直线上,点的横坐标为1,过点作轴,垂足为,以为边向右作正方形,延长交直线l于点;以为边向右作正方形,延长交直线l于点;……;按照这个规律进行下去,点的坐标为___________.
【答案】
【解析】
【分析】
由题意分别求出A1、A2、A3、A4……An、B1、B2、B3、B4……Bn、的坐标,根据规律进而可求解.
【详解】
解:∵点在直线上,点的横坐标为1,过点作轴,垂足为,
∴,,∴A1B1=,
根据题意,OA2=1+=,
∴,,
同理,,,
,
……
由此规律,可得:,,
∴即,
故答案为:.
5.(2022·黑龙江)如图,在平面直角坐标系中,点,,,……在x轴上且,,,……按此规律,过点,,,……作x轴的垂线分别与直线交于点,,,……记,,,……的面积分别为,,,……,则______.
【答案】
【解析】
【分析】
先求出,可得,再根据题意可得,从而得到∽∽∽∽……∽,再利用相似三角形的性质,可得∶∶∶∶……∶= ,即可求解.
【详解】
解:当x=1时,,
∴点,
∴,
∴,
∵根据题意得:,
∴∽∽∽∽……∽,
∴∶∶∶:……∶= OA12∶OA22∶OA32∶……∶OAn2,
∵,,,,……,
∴,,,……,,
∴∶∶∶∶……∶= ,
∴,
∴.
故答案为:.
6.(2022·贵州毕节)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为_________.
【答案】
【分析】先根据平移规律得到第n次变换时,相当于把点的坐标向右或向左平移n个单位长度,再向右或向上平移n个单位长度得到下一个点,然后推出每四次坐标变换为一个循环,每一个循环里面横坐标不发生变化,纵坐标向下平移4个单位长度,从而求出点A8的坐标为(0,-8),由此求解即可.
【详解】解:∵把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点,
∴第n次变换时,相当于把点的坐标向右或向左平移n个单位长度,再向右或向上平移n个单位长度得到下一个点,
∵O到A1是向右平移1个单位长度,向上平移1个单位长度,A1到A2是向左2个单位长度,向上平移2个单位长度,A2到A3是向左平移3个单位长度,向下平移3个单位长度,A3到A4是向右平移4个单位长度,向下平移4个单位长度,A4到A5是向右平移5个单位长度,向上平移5个单位长度,
∴可以看作每四次坐标变换为一个循环,每一个循环里面横坐标不发生变化,纵坐标向下平移4个单位长度,
∴点A8的坐标为(0,-8),
∴点A8到A9的平移方式与O到A1的方式相同(只指平移方向)即A8到A9向右平移9个单位,向上平移9个单位,
∴A9的坐标为(9,1),
同理A9到A10的平移方式与A1到A2的平移方式相同(只指平移方向),即A9到A10向左平移10个单位,向上平移10个单位,
∴A10的坐标为(-1,11),
故答案为:(-1,11).
模块三 函数
专题1 平面直角坐标系和函数的概念
直角坐标系 平面直角坐标系 (1)对应关系:坐标平面内的点与有序实数对是一一对应的. (2)坐标轴上的点:x轴,y轴上的点不属于任何象限.
点的坐标特征 各象限内点的坐标特征:
坐标轴上点的特征: x轴上点的纵坐标为0; y轴上点的横坐标为0; 原点的坐标为(0,0).
对称点的坐标特征: 点P(x,y)关于x轴的对称点为P1(x,-y); 点P(x,y)关于y轴的对称点为P2(-x,y); 点P(x,y)关于原点的对称点为P3(-x,-y).
点的平移特征: 将点P(x,y)向右(或左)平移a个单位长度后得P'(x+a,y)(或P'(x-a,y)); 将点P(x,y)向上(或下)平移b个单位长度后得P″(x,y+b)(或P″(x,y-b)).
点到坐标轴的距离: 点P(x,y)到x轴的距离为|y|;到y轴的距离为|x|.
函数的认识 函数的有关概念 变量与常量: 在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
函数的概念: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
表示方法: 解析式法、列表法、图象法.
自变量的 取值范围 ① 解析式是整式时,自变量的取值范围是全体实数; ② 解析式是分式时,自变量的取值范围是分母不为0的实数; ③ 解析式是二次根式时,自变量的取值范围是被开方数大于等于0;
函数值: 对于一个函数,如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
函数的图象 函数图象的概念: 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数图象的画法: 列表、描点、连线.
题型一、平面直角坐标系的点的特征
1.(2022·四川乐山)点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022·湖南长沙)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
3.(2022·广东)在平面直角坐标系中,将点向右平移2个单位后,得到的点的坐标是( )
A. B. C. D.
4.(2022·四川雅安)在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为( )
A.﹣4 B.4 C.12 D.﹣12
5.(2022·江苏扬州)在平面直角坐标系中,点P(﹣3,a2+1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022·贵州铜仁)如图,在矩形中,,则D的坐标为( )
A. B. C. D.
7.(2022·四川广安)若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第________象限.
题型二、函数的相关概念及图象
1.(2022·广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为.下列判断正确的是( )
A.2是变量 B.是变量 C.r是变量 D.C是常量
2.(2022·上海)已知f(x)=3x,则f(1)=_____.
3.(2022·黑龙江大庆)在函数中,自变量的取值范围是_________.
4.(2022·黑龙江绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
5.(2022·黑龙江齐齐哈尔)如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )
A.AF=5 B.AB=4 C.DE=3 D.EF=8
6.(2022·贵州毕节)现代物流的高速发展,为乡村振兴提供了良好条件,某物流公司的汽车行驶后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶到达目的地.汽车行驶的时间x(单位:h)与行驶的路程y(单位:)之间的关系如图所示,请结合图象,判断以下说法正确的是( )
A.汽车在高速路上行驶了 B.汽车在高速路上行驶的路程是
C.汽车在高速路上行驶的平均速度是 D.汽车在乡村道路上行驶的平均速度是
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
7.(2022·湖北随州)已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
A.张强从家到体育场用了15min B.体育场离文具店1.5km
C.张强在文具店停留了20min D.张强从文具店回家用了35min
8.(2022·内蒙古赤峰)已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是_________.(填写所有正确结论的序号)
①体育场离王强家 ②王强在体育场锻炼了
③王强吃早餐用了 ④王强骑自行车的平均速度是
9.(2022·湖北鄂州)在“看图说故事”话动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)小明家离体育场的距离为 km,小明跑步的平均速度为 km/min;
(2)当15≤x≤45时,请直接写出y关于x的函数表达式;
(3)当小明离家2km时,求他离开家所用的时间.
10.(2022·黑龙江齐齐哈尔)在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y (米)与出发时间x (分钟)之间的函数关系如图所示,请结合图像解答下列问题:
(1)A、B两地之间的距离是 米,乙的步行速度是 米/分;
(2)图中a= ,b= ,c= ;
(3)求线段MN的函数解析式;
(4)在乙运动的过程中,何时两人相距80米 (直接写出答案即可)
11.(2022·黑龙江)为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)甲车速度是_______km/h,乙车出发时速度是_______km/h;
(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);
(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.
题型三、动点问题的函数图像判断
1.(2022·甘肃武威)如图1,在菱形中,,动点从点出发,沿折线方向匀速运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2所示,则的长为( )
A. B. C. D.
2.(2022·辽宁)如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A.B.C.D.
3.如图,在 中,,,,点 E 在 边上由点 A 向点 B 运动(不与点 A,点 B 重合),过点E 作 垂直 交直角边于 F.设, 面积为 y,则 y 关于 x 的函数图象大致是( )
A.B.C. D.
4.如图,点是菱形的对角线上的一个动点,过点垂直于的直线交菱形的边于、两点.设,,,的面积为y,则y关于x的函数图象大致形状是( )
A.B.C. D.
5.(2021·新疆)如图,在矩形ABCD中,,.点P从点A出发,以2cm/s的速度在矩形的边上沿运动,当点P与点D重合时停止运动.设运动的时间为(单位:s),的面积为S(单位:),则S随t变化的函数图象大致为( )
A. B.
C. D.
6.如图,在菱形ABCD中,其边长为4cm,,垂直于AD的直线EF(直线EF与菱形ABCD的两边分别交于点E,F,且点E在点F的上方)从点A出发,沿AD方向以每秒1cm的速度向右平移.若的面积为,直线EF的运动时间为,则下列能大致反映y与x的函数关系的图象是( )
A. B.C. D.
7.(2022·山东潍坊)如图,在 ABCD中,∠A=60°,AB=2,AD=1,点E,F在 ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A. B.
C. D.
8.(2022·辽宁)如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
题型四、平面直角坐标系的规律探究
1.(2022 河南)如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2 022次旋转结束时,点A的坐标为( )
A.(,-1) B.(-1,-) C.(-,-1) D.(1,)
2.(2022·黑龙江齐齐哈尔)如图,直线与轴相交于点,与轴相交于点,过点作交轴于点,过点作轴交于点,过点作交轴于点,过点作轴交于点…,按照如此规律操作下去,则点的纵坐标是______.
3.(2021·贵州毕节)如图,在平面直角坐标系中,点在直线上,过点作,交轴于点;过点作轴,交直线于点;过点作,交轴于点;过点作轴,交直线于点;…;按此作法进行下去,则点的坐标为_____________.
4.(2021·内蒙古呼伦贝尔)如图,点在直线上,点的横坐标为1,过点作轴,垂足为,以为边向右作正方形,延长交直线l于点;以为边向右作正方形,延长交直线l于点;……;按照这个规律进行下去,点的坐标为___________.
5.(2022·黑龙江)如图,在平面直角坐标系中,点,,,……在x轴上且,,,……按此规律,过点,,,……作x轴的垂线分别与直线交于点,,,……记,,,……的面积分别为,,,……,则______.
6.(2022·贵州毕节)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为_________.
2023年中考数学第一轮复习
模块三 函数
专题1 平面直角坐标系和函数的概念
知识梳理
直角坐标系 平面直角坐标系 (1)对应关系:坐标平面内的点与有序实数对是一一对应的. (2)坐标轴上的点:x轴,y轴上的点不属于任何象限.
点的坐标特征 各象限内点的坐标特征:
坐标轴上点的特征: x轴上点的纵坐标为0; y轴上点的横坐标为0; 原点的坐标为(0,0).
对称点的坐标特征: 点P(x,y)关于x轴的对称点为P1(x,-y); 点P(x,y)关于y轴的对称点为P2(-x,y); 点P(x,y)关于原点的对称点为P3(-x,-y).
点的平移特征: 将点P(x,y)向右(或左)平移a个单位长度后得P'(x+a,y)(或P'(x-a,y)); 将点P(x,y)向上(或下)平移b个单位长度后得P″(x,y+b)(或P″(x,y-b)).
点到坐标轴的距离: 点P(x,y)到x轴的距离为|y|;到y轴的距离为|x|.
函数的认识 函数的有关概念 变量与常量: 在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
函数的概念: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
表示方法: 解析式法、列表法、图象法.
自变量的 取值范围 ① 解析式是整式时,自变量的取值范围是全体实数; ② 解析式是分式时,自变量的取值范围是分母不为0的实数; ③ 解析式是二次根式时,自变量的取值范围是被开方数大于等于0;
函数值: 对于一个函数,如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
函数的图象 函数图象的概念: 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数图象的画法: 列表、描点、连线.
题型梳理
题型一、平面直角坐标系的点的特征
1.(2022·四川乐山)点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】根据各象限内点的坐标特征解答即可.
【详解】解:点( 1,2)所在的象限是第二象限.故选:B.
2.(2022·湖南长沙)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
【答案】D
【分析】根据关于原点对称的两个点,横坐标、纵坐标分别互为相反数,即可求解.
【详解】解:点关于原点对称的点的坐标是.故选D.
3.(2022·广东)在平面直角坐标系中,将点向右平移2个单位后,得到的点的坐标是( )
A. B. C. D.
【答案】A
【分析】把点的横坐标加2,纵坐标不变,得到,就是平移后的对应点的坐标.
【详解】解:点向右平移2个单位长度后得到的点的坐标为.
故选A.
4.(2022·四川雅安)在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为( )
A.﹣4 B.4 C.12 D.﹣12
【答案】D
【分析】首先根据关于原点对称的点的坐标特点可得,可得a,b的值,再代入求解即可得到答案.
【详解】解: 点(a+2,2)关于原点的对称点为(4,﹣b),
,
解得:
故选D
5.(2022·江苏扬州)在平面直角坐标系中,点P(﹣3,a2+1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【详解】∵a2 0,∴a2+1 1,∴点P( 3,a2+1)所在的象限是第二象限.故选B.
6.(2022·贵州铜仁)如图,在矩形中,,则D的坐标为( )
A. B. C. D.
【答案】D
【分析】先根据A、B的坐标求出AB的长,则CD=AB=6,并证明轴,同理可得轴,由此即可得到答案.
【详解】解:∵A(-3,2),B(3,2),
∴AB=6,轴,
∵四边形ABCD是矩形,
∴CD=AB=6,轴,
同理可得轴,
∵点C(3,-1),
∴点D的坐标为(-3,-1),
故选D.
7.(2022·四川广安)若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第________象限.
【答案】二
【分析】根据点P(m+1,m)在第四象限,可得到,从而得到,即可求解.
【详解】解:∵点P(m+1,m)在第四象限,
∴,解得:,
∴,
∴点Q(﹣3,m+2)在第二象限.
故答案为:二
题型二、函数的相关概念及图象
1.(2022·广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为.下列判断正确的是( )
A.2是变量 B.是变量 C.r是变量 D.C是常量
【答案】C
【分析】根据变量与常量的定义分别判断,并选择正确的选项即可.
【详解】解:2与π为常量,C与r为变量,
故选C.
2.(2022·上海)已知f(x)=3x,则f(1)=_____.
【答案】3
【分析】直接代入求值即可.
【详解】解:∵f(x)=3x,∴f(1)=3×1=3,故答案为:3
3.(2022·黑龙江大庆)在函数中,自变量的取值范围是_________.
【答案】
【分析】二次根式内非负,则函数有意义.
【详解】要使函数有意义,则二次根式内为非负
∴2x+3≥0
解得:
故答案为:
4.(2022·黑龙江绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
【答案】C
【分析】先根据题意求得A、D、E、F的坐标,然后再运用待定系数法分别确定AE、AF、OD的解析式,再分别联立OD与AE和AF求得两次相遇的时间,最后作差即可.
【详解】解: 如图:根据题意可得A(8,a),D(12,a),E(4,0),F(12,0)
设AE的解析式为y=kx+b,则 ,解得
∴直线AE的解析式为y=x-3a
同理:直线AF的解析式为:y=-x+3a,直线OD的解析式为:y=
联立 ,解得
联立 ,解得
两人先后两次相遇的时间间隔为9-6=3min.
故答案为C.
5.(2022·黑龙江齐齐哈尔)如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )
A.AF=5 B.AB=4 C.DE=3 D.EF=8
【答案】B
【分析】路线为A→B→C→D→E,将每段路线在坐标系中对应清楚即可得出结论.
【详解】解:坐标系中对应点运动到B点
B选项正确
即:
解得:
A选项错误
12~16s对应的DE段
C选项错误
6~12s对应的CD段
D选项错误故选:B.
6.(2022·贵州毕节)现代物流的高速发展,为乡村振兴提供了良好条件,某物流公司的汽车行驶后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶到达目的地.汽车行驶的时间x(单位:h)与行驶的路程y(单位:)之间的关系如图所示,请结合图象,判断以下说法正确的是( )
A.汽车在高速路上行驶了 B.汽车在高速路上行驶的路程是
C.汽车在高速路上行驶的平均速度是 D.汽车在乡村道路上行驶的平均速度是
【答案】D
【分析】观察图象可得汽车在高速路上行驶了3.5-0.5-1=2h;汽车在高速路上行驶的路程是180-30=150km;汽车在高速路上行驶的平均速度是150÷2=75km/h;汽车在乡村道路上行驶的平均速度是(220-180)÷1=40km/h,即可求解.
【详解】解:A、根据题意得:汽车在高速路上行驶了3.5-0.5-1=2h,故本选项错误,不符合题意;
B、汽车在高速路上行驶的路程是180-30=150km,故本选项错误,不符合题意;
C、汽车在高速路上行驶的平均速度是150÷2=75km/h,故本选项错误,不符合题意;
D、汽车在乡村道路上行驶的平均速度是(220-180)÷1=40km/h,故本选项正确,符合题意;选:D
7.(2022·湖北随州)已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
A.张强从家到体育场用了15min B.体育场离文具店1.5km
C.张强在文具店停留了20min D.张强从文具店回家用了35min
【答案】B
【分析】利用图象信息解决问题即可.
【详解】解:由图可知:
A. 张强从家到体育场用了15min,正确,不符合题意;
B. 体育场离文具店的距离为:,故选项错误,符合题意;
C. 张强在文具店停留了:,正确,不符合题意;
D. 张强从文具店回家用了,正确,符合题意,
故选:B.
8.(2022·内蒙古赤峰)已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是_________.(填写所有正确结论的序号)
①体育场离王强家 ②王强在体育场锻炼了
③王强吃早餐用了 ④王强骑自行车的平均速度是
【答案】①③④
【分析】利用图象信息解决问题即可.
【详解】解:体育场离张强家,①正确;
王强在体育场锻炼了,②错误;
王强吃早餐用了,③正确;
王强骑自行车的平均速度是,④正确.
故答案为:①③④.
9.(2022·湖北鄂州)在“看图说故事”话动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)小明家离体育场的距离为 km,小明跑步的平均速度为 km/min;
(2)当15≤x≤45时,请直接写出y关于x的函数表达式;
(3)当小明离家2km时,求他离开家所用的时间.
【答案】(1)2.5;;
(2)
(3)当小明离家2km时,他离开家所用的时间为12min或37.5min
【分析】(1)根据函数图象结合路程=时间×速度进行求解即可;
(2)分当时和当时两种情况讨论求解即可;
(3)分当小明处在去体育馆的途中离家2km时,当小明从体育馆去商店途中离家2kn时两种情况讨论求解即可.
(1)
解:由函数图象可知小明在离家15分钟时到底体育馆,此时离家的距离为2.5km,
∴小明家离体育馆的距离为2.5km,小明跑步的平均速度为,
故答案为:2.5;;
(2)
解:由函数图象可知当时,,
当时,此时y是关于x一次函数,设,
∴,
解得,
∴此时,
综上所述,
(3)
解:当小明处在去体育馆的途中离家2km时,
;
当小明从体育馆去商店途中离家2km时,
∴,
解得;
综上所述,当小明离家2km时,他离开家所用的时间为12min或37.5min.
10.(2022·黑龙江齐齐哈尔)在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y (米)与出发时间x (分钟)之间的函数关系如图所示,请结合图像解答下列问题:
(1)A、B两地之间的距离是 米,乙的步行速度是 米/分;
(2)图中a= ,b= ,c= ;
(3)求线段MN的函数解析式;
(4)在乙运动的过程中,何时两人相距80米 (直接写出答案即可)
【答案】(1)1200,60
(2)900,800,15
(3)y =-20x+1200(15≤x≤20)
(4)8分钟,分钟
【分析】(1)分析图像,出发前两人之间的距离即为A、B两地之间的距离,为1200米,乙经过20分钟时到达A地,所以乙的速度为可计算出来;
(2)由函数图像可知,经过分钟时两人相遇,则可算出甲的速度,经过c分钟时两人距离重新达到最大,此时甲到达B地,则可求出a,经过20分钟时乙到达A地,此时两人相距b米,利用甲乙的速度即可算出b;
(3)由(2)可知M、N的坐标,设出MN的一般解析式,将M、N的坐标代入即可求出;
(4)设经过x分钟两人相距80米,根据两人相遇前和相遇后都可相距80米分别列方程即可求出.
(1)
由函数图像可知,最开始时甲乙两人之间的距离为1200米,
因为甲从A地出发,乙从B地出发,两人最开始时的距离就是A、B两地之间的距离,
所以A、B两地之间距离为1200米;
由图像可知乙经过20分时到达A地,
∴乙的步行速度为(米/分);
故答案为:1200,60;
(2)
由函数图像可知,经过分钟时两人相遇,经过c分钟时两人距离重新达到最大,此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,
设甲的步行速度为x米/分,则,
解得:x=80(米/分)
∴(分),
(米),
(米).
故答案为:900,800,15;
(3)
由(2)可知,M、N的坐标分别为M(15,900),N(20,800),
设线段MN的解析式为y=kx+b(),
则有 ,
解得:
∴线段MN的函数解析式是y =-20x+1200(15≤x≤20)
(4)
设经过x分钟两人相距80米,两人相遇前和相遇后都可相距80米,
相遇前:1200-(60+80)x=80,解得:x=8;
相遇后:(60+80)x-1200=80,解得:x=,
所以经过8分钟和分钟时两人相距80米.
11.(2022·黑龙江)为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)甲车速度是_______km/h,乙车出发时速度是_______km/h;
(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);
(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.
【答案】(1)100 60
(2)
(3)3,6.3,9.125
【分析】(1)根据图象分别得出甲车5h的路程为500km,乙车5h的路程为300km,即可确定各自的速度;
(2)设,由图象可得经过点(9,300),(12,0)点,利用待定系数法即可确定函数解析式;
(3)乙出发的时间为t时,相距120km,根据图象分多个时间段进行分析,利用速度与路程、时间的关系求解即可.
(1)
解:根据图象可得,甲车5h的路程为500km,
∴甲的速度为:500÷5=100km/h;
乙车5h的路程为300km,
∴乙的速度为:300÷5=60km/h;
故答案为:100;60;
(2)
设,由图象可得经过点(9,300),(12,0)点,
代入得,
解得
∴y与x的函数解析式为;
(3)
解:设乙出发的时间为t时,相距120km,
根据图象可得,
当0
解得:t=3;
当5
解得:t=6.3;
当8
解得:t=12.2,不符合题意,舍去;
当9
解得:t=9.125;
综上可得:乙车出发3h、6.3h与9.125h时,两车之间的距离为120km.
题型三、动点问题的函数图像判断
1.(2022·甘肃武威)如图1,在菱形中,,动点从点出发,沿折线方向匀速运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2所示,则的长为( )
A. B. C. D.
【答案】B
【分析】根据图1和图2判定三角形ABD为等边三角形,它的面积为解答即可.
【详解】解:在菱形ABCD中,∠A=60°,
∴△ABD为等边三角形, 设AB=a,由图2可知,△ABD的面积为,
∴△ABD的面积 解得:a= 故选B
2.(2022·辽宁)如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A.B.C.D.
【答案】A
【分析】分三种情形∶ ①当0<x≤2时, 重叠部分为△CDG,②当2<x≤4时,重叠部分为四边形AGDC,③当4<x≤8时,重叠部分为△BEG,分别计算即可.
【详解】解:过点A作AM⊥BC,交BC于点M,
在等边△ABC中,∠ACB=60°,
在Rt△DEF中,∠F=30°,
∴∠FED=60°,
∴∠ACB=∠FED,
∴ACEF,
在等边△ABC中,AM⊥BC,
∴BM=CM=BC=2,AM=BM=2,
∴S△ABC=BC AM=4,
①当0<x≤2时,设AC与DF交于点G,此时△ABC与Rt△DEF重叠部分为△CDG,
由题意可得CD=x,DG=x
∴S=CD DG=x2;
②当2<x≤4时,设AB与DF交于点G,此时△ABC与Rt△DEF重叠部分为四边形AGDC,
由题意可得:CD=x,则BD=4﹣x,DG=(4﹣x),
∴S=S△ABC﹣S△BDG=4﹣×(4﹣x)×(4﹣x),
∴S=﹣x2+4x﹣4=﹣(x﹣4)2+4,
③当4<x≤8时,设AB与EF交于点G,过点G作GM⊥BC,交BC于点M,
此时△ABC与Rt△DEF重叠部分为△BEG,
由题意可得CD=x,则CE=x﹣4,DB=x﹣4,
∴BE=x﹣(x﹣4)﹣(x﹣4)=8﹣x,
∴BM=4﹣x
在Rt△BGM中,GM=(4﹣x),
∴S=BE GM=(8﹣x)×(4﹣x),
∴S=(x﹣8)2,
综上,选项A的图像符合题意,
故选:A.
3.如图,在 中,,,,点 E 在 边上由点 A 向点 B 运动(不与点 A,点 B 重合),过点E 作 垂直 交直角边于 F.设, 面积为 y,则 y 关于 x 的函数图象大致是( )
A.B.C. D.
【答案】D
【分析】过点作于点,利用勾股定理以及面积法求得的长,分和两种情况讨论,利用相似三角形的判定和性质求解即可;
【详解】解:过点作于点,
,
,
,
,
当,
,
,
,
,即,
,
,开口向上的一段抛物线;
当,
同理可证,
,即,
,
,开口向下的一段抛物线;
综上,符合题意的函数关系的图象是D;
故选:D.
4.如图,点是菱形的对角线上的一个动点,过点垂直于的直线交菱形的边于、两点.设,,,的面积为y,则y关于x的函数图象大致形状是( )
A.B.C. D.
【答案】A
【分析】的面积,通过题干已知条件,用分别表示出、,根据所得的函数,利用其图象,可分两种情况解答:①;②.
【详解】解:①当时,如图1,
在菱形中,,,,且;
,
∴
,
,
即,
,
,
,
函数图象开口向下;
②当,如图2,
同理证得,,
,
即,
,
,
,
函数图象开口向上;
综上,答案A的图象大致符合;
故选:A.
5.(2021·新疆)如图,在矩形ABCD中,,.点P从点A出发,以2cm/s的速度在矩形的边上沿运动,当点P与点D重合时停止运动.设运动的时间为(单位:s),的面积为S(单位:),则S随t变化的函数图象大致为( )
A. B. C. D.
【答案】D
【解析】
【分析】
分点P在AB上运动, 0≤t≤4;点P在BC上运动, 4<t≤7;点P在CD上运动, 7<t≤11,分别计算即可
【详解】
当点P在AB上运动时, S==6t,0≤t≤4;
当点P在BC上运动时, S==24,4<t≤7;
点P在CD上运动, S=, 7<t≤11,
故选D.
6.如图,在菱形ABCD中,其边长为4cm,,垂直于AD的直线EF(直线EF与菱形ABCD的两边分别交于点E,F,且点E在点F的上方)从点A出发,沿AD方向以每秒1cm的速度向右平移.若的面积为,直线EF的运动时间为,则下列能大致反映y与x的函数关系的图象是( )
A. B.
C. D.
【答案】D
【分析】根据,分别求出EF的长度代入即可判断函数图象.
【详解】解:∵四边形ABCD是菱形,边长为4,∠A=60°,
∴当E、B重合时,AF=2,
当,,,
∴,
即,
∴y与x的函数是开口向上的二次函数,图象为抛物线的一部分;
当,EF为常数=,
∴,
即,
∴y与x是正比例函数,图象为直线的一部分,
故选:D.
7.(2022·山东潍坊)如图,在 ABCD中,∠A=60°,AB=2,AD=1,点E,F在 ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A. B. C. D.
【答案】A
【分析】分0≤x≤1,1
∵∠A=60°,AE=AF=x,
∴AG=x,
由勾股定理得FG=x,
∴y=AE×FG=x2,图象是一段开口向上的抛物线;
当1
∴AH=,
由勾股定理得DH=,
∴y=(DF+AE)×DH=x-,图象是一条线段;
当2≤x≤3时,过点E作EI⊥CD于点I,
∵∠C=∠DAB=60°,CE=CF=3-x,
同理求得EI=(3-x),
∴y= AB×DH -CF×EI=-(3-x)2=-x2+x-,图象是一段开口向下的抛物线;
观察四个选项,只有选项A符合题意,故选:A.
【点睛】本题考查了利用分类讨论的思想求动点问题的函数图象;也考查了平行四边形的性质,含30度的直角三角形的性质,勾股定理,三角形的面积公式以及一次函数和二次函数的图象.
8.(2022·辽宁)如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
【答案】D
【分析】由题意易得,,则有,进而可分当点P在AB中点的左侧时和在AB中点的右侧时,然后分类求解即可.
【详解】解:∵,
∴,由题意知:,∴,
由折叠的性质可得:,
当点P与AB中点重合时,则有,
当点P在AB中点的左侧时,即,
∴与重叠部分的面积为;
当点P在AB中点的右侧时,即,如图所示:
由折叠性质可得:,,
∴,∴,∴,
∴与重叠部分的面积为;
综上所述:能反映与重叠部分的面积S与t之间函数关系的图象只有D选项;故选D.
题型四、平面直角坐标系的规律探究
1.(2022 河南)如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2 022次旋转结束时,点A的坐标为( )
A.(,-1) B.(-1,-) C.(-,-1) D.(1,)
2.(2022·黑龙江齐齐哈尔)如图,直线与轴相交于点,与轴相交于点,过点作交轴于点,过点作轴交于点,过点作交轴于点,过点作轴交于点…,按照如此规律操作下去,则点的纵坐标是______.
【答案】
【分析】先根据30°的特殊直角三角形,如,,,求出B点,B1点的纵坐标,发现规律,即可
【详解】∵
当时,
当时,
故,
∴为30°的直角三角形
∴
∵
∴为30°的直角三角形
∴
∴为30°的直角三角形
∵轴
∴
∴
为30°的直角三角形
同理:
…
故:
故答案为:
3.(2021·贵州毕节)如图,在平面直角坐标系中,点在直线上,过点作,交轴于点;过点作轴,交直线于点;过点作,交轴于点;过点作轴,交直线于点;…;按此作法进行下去,则点的坐标为_____________.
【答案】(,0).
【解析】
【分析】
根据题目所给的解析式,求出对应的坐标,然后根据规律求出的坐标,最后根据题目要求求出最后答案即可.
【详解】
解:如图,过点N作NM⊥x轴于M
将代入直线解析式中得
∴,45°
∵90°
∴
∵
∴
∴的坐标为(2,0)
同理可以求出的坐标为(4,0)
同理可以求出的坐标为(8,0)
同理可以求出的坐标为(,0)
∴的坐标为(,0)
故答案为:(,0).
4.(2021·内蒙古呼伦贝尔)如图,点在直线上,点的横坐标为1,过点作轴,垂足为,以为边向右作正方形,延长交直线l于点;以为边向右作正方形,延长交直线l于点;……;按照这个规律进行下去,点的坐标为___________.
【答案】
【解析】
【分析】
由题意分别求出A1、A2、A3、A4……An、B1、B2、B3、B4……Bn、的坐标,根据规律进而可求解.
【详解】
解:∵点在直线上,点的横坐标为1,过点作轴,垂足为,
∴,,∴A1B1=,
根据题意,OA2=1+=,
∴,,
同理,,,
,
……
由此规律,可得:,,
∴即,
故答案为:.
5.(2022·黑龙江)如图,在平面直角坐标系中,点,,,……在x轴上且,,,……按此规律,过点,,,……作x轴的垂线分别与直线交于点,,,……记,,,……的面积分别为,,,……,则______.
【答案】
【解析】
【分析】
先求出,可得,再根据题意可得,从而得到∽∽∽∽……∽,再利用相似三角形的性质,可得∶∶∶∶……∶= ,即可求解.
【详解】
解:当x=1时,,
∴点,
∴,
∴,
∵根据题意得:,
∴∽∽∽∽……∽,
∴∶∶∶:……∶= OA12∶OA22∶OA32∶……∶OAn2,
∵,,,,……,
∴,,,……,,
∴∶∶∶∶……∶= ,
∴,
∴.
故答案为:.
6.(2022·贵州毕节)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为_________.
【答案】
【分析】先根据平移规律得到第n次变换时,相当于把点的坐标向右或向左平移n个单位长度,再向右或向上平移n个单位长度得到下一个点,然后推出每四次坐标变换为一个循环,每一个循环里面横坐标不发生变化,纵坐标向下平移4个单位长度,从而求出点A8的坐标为(0,-8),由此求解即可.
【详解】解:∵把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点,
∴第n次变换时,相当于把点的坐标向右或向左平移n个单位长度,再向右或向上平移n个单位长度得到下一个点,
∵O到A1是向右平移1个单位长度,向上平移1个单位长度,A1到A2是向左2个单位长度,向上平移2个单位长度,A2到A3是向左平移3个单位长度,向下平移3个单位长度,A3到A4是向右平移4个单位长度,向下平移4个单位长度,A4到A5是向右平移5个单位长度,向上平移5个单位长度,
∴可以看作每四次坐标变换为一个循环,每一个循环里面横坐标不发生变化,纵坐标向下平移4个单位长度,
∴点A8的坐标为(0,-8),
∴点A8到A9的平移方式与O到A1的方式相同(只指平移方向)即A8到A9向右平移9个单位,向上平移9个单位,
∴A9的坐标为(9,1),
同理A9到A10的平移方式与A1到A2的平移方式相同(只指平移方向),即A9到A10向左平移10个单位,向上平移10个单位,
∴A10的坐标为(-1,11),
故答案为:(-1,11).
同课章节目录
