【模块三 函数】专题2 一次函数-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块三 函数】专题2 一次函数-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 14:42:10 | ||
图片预览




文档简介
2023年中考数学第一轮复习
模块三 函数
专题2 一次函数
一次函数与正比例函数 一次函数与正比例函数的定义 如果y=kx+b(k≠0),那么y叫x的一次函数,当b=0时,一次函数y=kx也叫正比例函数.正比例函数是一次函数的特例,具有一次函数的性质.
一次函数与正比例函数的关系 一次函数y=kx+b(k≠0)的图象是过点(0,b)与直线y=kx平行的一条直线。它可以由直线y=kx平移得到.它与x轴的交点为,与y轴的交点为(0,b).
一次函数的 图象与性质 |k|越大,直线越陡; k相等,直线平行; b决定直线与y轴的交点(0,b) k>0 k<0
直线从左 向右上升 直线从左 向右下降
增减性 y随x的增大而增大 y随x的增大而减少
平移 当b>0时,图象向上平移b个单位长度; 当b<0时,图象向下平移|b|个单位长度.
确定一次函数解析式 确定一次函数的解析式 第一步:设,设出一次函数的一般形式y=kx+b(k≠0). 第二步:代,将已知点坐标代入解析式得出方程或方程组. 第三步:求,通过列方程或方程组求出待定系数k,b的值. 第四步:写,写出该函数的解析式.
与一元一次 方程的关系 一次函数y=kx+b与x轴交点的横坐标-是方程kx+b=0的解
与二元一次方程组的关系 一次函数y=kx+b与y=k1x+b1图象的交点坐标是方程组的解;反之,方程组的解是一次函数y=kx+b与y=k1x+b1图象的交点坐标
与一元一次不等式的关系 一次函数y=kx+b的函数值y>0时,自变量x的取值范围是kx+b>0的解集
一次函数y=kx+b的函数值y<0时,自变量x的取值范围是kx+b<0的解集
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
题型一、一次函数的概念与解析式
1.(2022·江苏泰州)一次函数的图像经过点(1,0).当y>0时,x的取值范围是__________.
2.(2022·湖南永州)已知一次函数的图象经过点,则______.
3.(2022 北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(-2,0),且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.
题型二、一次函数的图像与性质
1.(2022·内蒙古包头)在一次函数中,y的值随x值的增大而增大,且,则点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.(2022·四川广安)在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )
A.y=3x+5 B.y=3x﹣5 C.y=3x+1 D.y=3x﹣1
3.(2022·贵州遵义)若一次函数的函数值随的增大而减小,则值可能是( )
A.2 B. C. D.
4.(2022·辽宁锦州)点在一次函数的图像上,当时,,则a的取值范围是____________.
5.(2022·四川眉山)一次函数的值随的增大而增大,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022·湖南株洲)在平面直角坐标系中,一次函数的图象与轴的交点的坐标为( )
A. B. C. D.
7.(2022·湖南娄底)将直线向上平移2个单位,相当于( )
A.向左平移2个单位 B.向左平移1个单位 C.向右平移2个单位 D.向右平移1个单位
8.(2022·湖南邵阳)在直角坐标系中,已知点,点是直线上的两点,则,的大小关系是( )
A. B. C. D.
9.(2022·安徽)在同一平面直角坐标系中,一次函数与的图像可能是( )
A. B.C. D.
10.(2022·四川凉山)一次函数y=3x+b(b≥0)的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
题型三、一次函数与方程、不等式的关系
1.(2022·广西梧州)如图,在平面直角坐标系中,直线与直线相交于点A,则关于x,y的二元一次方程组的解是( )
A. B. C. D.
2.(2022·湖北鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
A.x>3 B.x<3 C.x<1 D.x>1
3.(2022·陕西)在同一平面直角坐标系中,直线与相交于点,则关于x,y的方程组的解为( )
A. B. C. D.
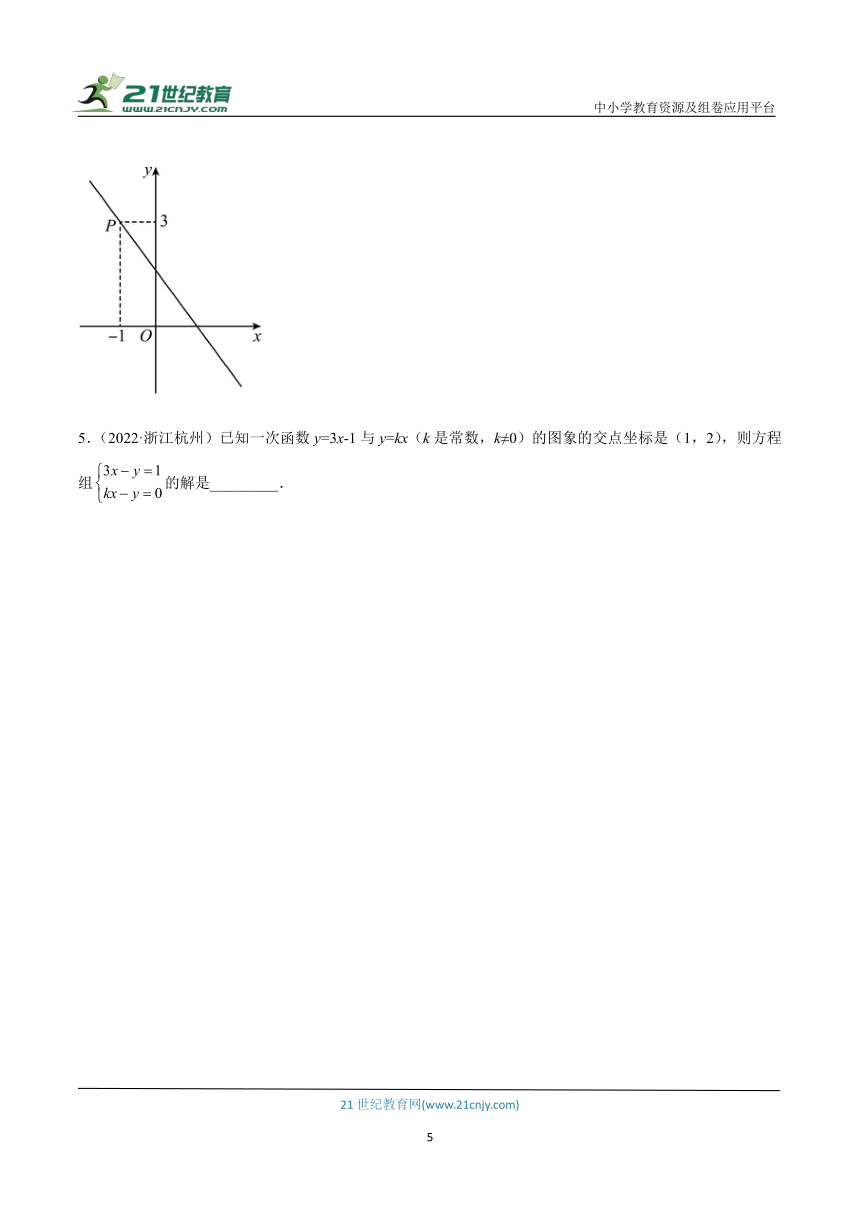
4.(2022·江苏扬州)如图,函数的图像经过点,则关于的不等式的解集为________.
5.(2022·浙江杭州)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组的解是_________.
题型四、一次函数的实际问题
1.(2022·内蒙古包头)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)求第14天小颖家草莓的日销售量;
(2)求当时,草莓价格m与x之间的函数关系式;
(3)试比较第8天与第10天的销售金额哪天多?
2.(2022·吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温(℃)与加热时间之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
(1)加热前水温是 ℃;
(2)求乙壶中水温关于加热时间的函数解析式;
(3)当甲壶中水温刚达到80℃时,乙壶中水温是 ℃.
3.(2022·浙江湖州)某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?
(2)如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;
(3)假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.
4.(2022·黑龙江牡丹江)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
(1)由于汽车发生故障,甲组在途中停留了___小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
题型五、一次函数的综合题
1.(2022·山东聊城)如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A., B.,
C., D.,
2.(2022·四川泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. B. C. D.
3.(2020·江苏南通)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
4.(2021·西藏)已知第一象限点P(x,y)在直线y=﹣x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
(2)当S=4时,求点P的坐标;
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
5.(2022·黑龙江牡丹江)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
2023年中考数学第一轮复习
模块三 函数
专题2 一次函数
知识梳理
一次函数与正比例函数 一次函数与正比例函数的定义 如果y=kx+b(k≠0),那么y叫x的一次函数,当b=0时,一次函数y=kx也叫正比例函数.正比例函数是一次函数的特例,具有一次函数的性质.
一次函数与正比例函数的关系 一次函数y=kx+b(k≠0)的图象是过点(0,b)与直线y=kx平行的一条直线。它可以由直线y=kx平移得到.它与x轴的交点为,与y轴的交点为(0,b).
一次函数的 图象与性质 |k|越大,直线越陡; k相等,直线平行; b决定直线与y轴的交点(0,b) k>0 k<0
直线从左 向右上升 直线从左 向右下降
增减性 y随x的增大而增大 y随x的增大而减少
平移 当b>0时,图象向上平移b个单位长度; 当b<0时,图象向下平移|b|个单位长度.
确定一次函数解析式 确定一次函数的解析式 第一步:设,设出一次函数的一般形式y=kx+b(k≠0). 第二步:代,将已知点坐标代入解析式得出方程或方程组. 第三步:求,通过列方程或方程组求出待定系数k,b的值. 第四步:写,写出该函数的解析式.
与一元一次 方程的关系 一次函数y=kx+b与x轴交点的横坐标-是方程kx+b=0的解
与二元一次方程组的关系 一次函数y=kx+b与y=k1x+b1图象的交点坐标是方程组的解;反之,方程组的解是一次函数y=kx+b与y=k1x+b1图象的交点坐标
与一元一次不等式的关系 一次函数y=kx+b的函数值y>0时,自变量x的取值范围是kx+b>0的解集
一次函数y=kx+b的函数值y<0时,自变量x的取值范围是kx+b<0的解集
题型梳理
题型一、一次函数的概念与解析式
1.(2022·江苏泰州)一次函数的图像经过点(1,0).当y>0时,x的取值范围是__________.
【答案】x<1
【分析】先用待定系数法,求出a的值.当y>0时,用含x的代数式表示y,解不等式即可.
【详解】解:把(1,0)代入一次函数,得
a+2=0,
解得:a=-2,
∴,
当y>0时,即,
解得:x<1.
故答案为:x<1.
2.(2022·湖南永州)已知一次函数的图象经过点,则______.
【答案】1
【分析】把点(m,2)代入一次函数y=x+1,列出关于m的一元一次方程,解之即可得m的值.
【详解】解:∵一次函数y=x+1的图象经过点(m,2)
∴把点(m,2)代入一次函数,得
m+1=2
解得:m=1
故答案为:1.
3.(2022 北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(-2,0),且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.
题型二、一次函数的图像与性质
1.(2022·内蒙古包头)在一次函数中,y的值随x值的增大而增大,且,则点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
【答案】B
【分析】根据一次函数的性质求出a的范围,再根据每个象限点的坐标特征判断A点所处的象限即可.
【详解】∵在一次函数中,y的值随x值的增大而增大,∴,即,
又∵,∴,∴点在第三象限,故选:B
2.(2022·四川广安)在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )
A.y=3x+5 B.y=3x﹣5 C.y=3x+1 D.y=3x﹣1
【答案】D
【分析】根据“上加下减,左加右减”的平移规律即可求解.
【详解】解:将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是y=3x﹣1,
故选:D
3.(2022·贵州遵义)若一次函数的函数值随的增大而减小,则值可能是( )
A.2 B. C. D.
【答案】D
【分析】根据一次函数的性质可得,即可求解.
【详解】解:∵一次函数的函数值随的增大而减小,
∴.
解得.
故选D.
4.(2022·辽宁锦州)点在一次函数的图像上,当时,,则a的取值范围是____________.
【答案】a<2
【分析】根据一次函数的性质,建立不等式计算即可.
【详解】∵当时,,
∴a-2<0,
∴a<2,
故答案为:a<2.
5.(2022·四川眉山)一次函数的值随的增大而增大,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】根据一次函数的性质求出m的范围,再根据每个象限点的坐标特征判断P点所处的象限即可.
【详解】∵一次函数的值随的增大而增大,
∴解得:∴在第二象限故选:B
6.(2022·湖南株洲)在平面直角坐标系中,一次函数的图象与轴的交点的坐标为( )
A. B. C. D.
【答案】D
【分析】令x=0,求出函数值,即可求解.
【详解】解:令x=0, ,
∴一次函数的图象与轴的交点的坐标为.故选:D
7.(2022·湖南娄底)将直线向上平移2个单位,相当于( )
A.向左平移2个单位 B.向左平移1个单位 C.向右平移2个单位 D.向右平移1个单位
【答案】B
【分析】函数图象的平移规律:左加右减,上加下减,根据规律逐一分析即可得到答案.
【详解】解:将直线向上平移2个单位,可得函数解析式为:
直线向左平移2个单位,可得 故A不符合题意;
直线向左平移1个单位,可得 故B符合题意;
直线向右平移2个单位,可得 故C不符合题意;
直线向右平移1个单位,可得 故D不符合题意;故选B
8.(2022·湖南邵阳)在直角坐标系中,已知点,点是直线上的两点,则,的大小关系是( )
A. B. C. D.
【答案】A
【分析】因为直线,所以随着自变量的增大,函数值会减小,根据这点即可得到问题解答.
【详解】解:∵因为直线,∴y随着x的增大而减小,
∵32>,∴∴m9.(2022·安徽)在同一平面直角坐标系中,一次函数与的图像可能是( )
A. B.C. D.
【答案】D
【分析】分为和两种情况,利用一次函数图像的性质进行判断即可.
【详解】解:当时,两个函数的函数值:,即两个图像都过点,故选项A、C不符合题意;
当时,,一次函数经过一、二、三象限,一次函数经过一、二、三象限,都与轴正半轴有交点,故选项B不符合题意;
当时,,一次函数经过一、二、四象限,与轴正半轴有交点,一次函数经过一、三、四象限,与轴负半轴有交点,故选项D符合题意.故选:D.
10.(2022·四川凉山)一次函数y=3x+b(b≥0)的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【分析】根据一次函数的性质可得其经过的象限,进而可得答案.
【详解】解:一次函数,
∵∴图象一定经过一、三象限,
∴当时,函数图象一定经过一、二、三象限,
当时,函数图象经过一、三象限,
∴函数图象一定不经过第四象限,故D正确.故选:D.
题型三、一次函数与方程、不等式的关系
1.(2022·广西梧州)如图,在平面直角坐标系中,直线与直线相交于点A,则关于x,y的二元一次方程组的解是( )
A. B. C. D.
【答案】B
【分析】由图象交点坐标可得方程组的解.
【详解】解:由图象可得直线与直线相交于点A(1,3),
∴关于x,y的二元一次方程组的解是.故选:B.
2.(2022·湖北鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
A.x>3 B.x<3 C.x<1 D.x>1
【答案】A
【分析】根据不等式kx+b<x的解集即为一次函数图象在正比例函数图象下方的自变量的取值范围求解即可
【详解】解:由函数图象可知不等式kx+b<x的解集即为一次函数图象在正比例函数图象下方的自变量的取值范围,
∴当kx+b<x时,x的取值范围是,
故选A.
3.(2022·陕西)在同一平面直角坐标系中,直线与相交于点,则关于x,y的方程组的解为( )
A. B. C. D.
【答案】C
【分析】先把点P代入直线求出n,再根据二元一次方程组与一次函数的关系求解即可;
【详解】解:∵直线与直线交于点P(3,n),
∴,∴,∴,∴1=3×2+m,∴m=-5,
∴关于x,y的方程组的解;故选:C.
4.(2022·江苏扬州)如图,函数的图像经过点,则关于的不等式的解集为________.
【答案】
【分析】观察一次函数图象,可知当y>3时,x的取值范围是,则的解集亦同.
【详解】由一次函数图象得,当y>3时,,
则y=kx+b>3的解集是.
5.(2022·浙江杭州)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组的解是_________.
【答案】
【分析】根据一次函数的交点坐标即可确定以两个一次函数解析式组成的二元一次方程组的解.
【详解】解:∵一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),
∴联立y=3x-1与y=kx的方程组的解为:,
即的解为:,故答案为:.
题型四、一次函数的实际问题
1.(2022·内蒙古包头)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)求第14天小颖家草莓的日销售量;
(2)求当时,草莓价格m与x之间的函数关系式;
(3)试比较第8天与第10天的销售金额哪天多?
【答案】(1)40千克(2)(3)第10天的销售金额多
【分析】(1)把x=14代入求出y值即可;
(2)用待定系数法求解,设m与x之间的函数关系式为,把(4,24),(12,16)代入,求出k,b值即可求解;
(3)把x=8,x=10分别代入y=12x,求出y,再把x=8,x=10分别代入(2)问所求解析式求出m值,然后分别求出my值,比较即可求解.
(1)解:∵当时,,
∴当时,(千克).
∴第14天小颖家草莓的日销售量是40千克.
(2)解:当时,设草莓价格m与x之间的函数关系式为,
∵点在的图像上,
∴解得
∴函数关系式为.
(3)解:∵当时,,
∴当时,,
当时,.
∵当时,,
∴当时,,当时,.
∴第8天的销售金额为:(元),
第10天的销售金额为:(元).
∵,∴第10天的销售金额多.
2.(2022·吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温(℃)与加热时间之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
(1)加热前水温是 ℃;
(2)求乙壶中水温关于加热时间的函数解析式;
(3)当甲壶中水温刚达到80℃时,乙壶中水温是 ℃.
【答案】(1)20 (2) (3)65
【分析】(1)根据时,即可得;
(2)先判断出乙壶对应的函数图象经过点,再利用待定系数法即可得;
(3)先利用待定系数法求出甲壶中与的函数解析式,再求出时,的值,然后将的值代入乙壶中与的函数解析式即可得.
(1)解:由函数图象可知,当时,,
则加热前水温是,故答案为:20.
(2)解:因为甲壶比乙壶加热速度快,
所以乙壶对应的函数图象经过点,
设乙壶中水温关于加热时间的函数解析式为,
将点代入得:,解得,
则乙壶中水温关于加热时间的函数解析式为,
自变量x的取值范围是0≤x≤160.
(3)解:设甲壶中水温关于加热时间的函数解析式为,
将点代入得:,解得,
则甲壶中水温关于加热时间的函数解析式为,
当时,,解得,
将代入得:,
即当甲壶中水温刚达到时,乙壶中水温是,故答案为:65.
3.(2022·浙江湖州)某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?
(2)如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;
(3)假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.
【答案】(1)轿车出发后2小时追上大巴,此时,两车与学校相距120千米
(2)点B的坐标是,s=60t-60(3)小时
【分析】(1)设轿车行驶的时间为x小时,则大巴行驶的时间为小时,根据路程两车行驶的路程相等得到即可求解;
(2)由(1)中轿车行驶的时间求出点B的坐标是,进而求出直线AB的解析式;
(3)根据大巴车行驶路程与小轿车行驶路程相等即可得到,进而求出a的值
(1)解:设轿车行驶的时间为x小时,则大巴行驶的时间为小时.
根据题意,得:,
解得x=2.
则千米,
∴轿车出发后2小时追上大巴,此时,两车与学校相距120千米.
(2)解:∵轿车追上大巴时,大巴行驶了3小时,
∴点B的坐标是.
由题意,得点A的坐标为.
设AB所在直线的解析式为,
则:
解得k=60,b=-60.
∴AB所在直线的解析式为s=60t-60.
(3)解:由题意,得,
解得:,
故a的值为小时.
4.(2022·黑龙江牡丹江)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
(1)由于汽车发生故障,甲组在途中停留了___小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
【答案】(1)1.9(2)270(3)按图象所表示的走法符合约定,理由见解析
【分析】(1)由于线段AB与x轴平行,故自3时到4.9时这段时间内甲组停留在途中,所以停留的时间为1.9时.(2)观察图象可知点B的纵坐标就是甲组的汽车在排除故障时距出发点的路程的千米数,从而求得直线EF和直线BD的解析式,即可求出B点的坐标.(3)由图象可知:甲、乙两组第一次相遇后在B和D相距最远,在两点处时, ,分别同25比较即可.
(1)4.9-3=1.9小时;故答案为:1.9
(2)设直线EF的解析式为y乙=kx+b,
∵点E(1.25,0)、点F(7.25,480)均在直线EF上,
∴,解得.
∴直线EF的解析式是y乙=80x﹣100.
∵点C在直线EF上,且点C的横坐标为6,
∴点C的纵坐标为80×6﹣100=380.
∴点C的坐标是(6,380).
设直线BD的解析式为y甲=mx+n;
∵点C(6,380)、点D(7,480)在直线BD上,
∴,解得.
∴BD的解析式是y甲=100x﹣220.
∵B点在直线BD上且点B的横坐标为4.9,代入y甲得B(4.9,270),
∴甲组在排除故障时,距出发点的路程是270千米.
(3)符合约定.理由如下:
由图象可知:甲、乙两组第一次相遇后在B和D相距最远,
在点B处有y乙﹣y甲=80×4.9﹣100﹣(100×4.9﹣220)=22千米<25千米,
在点D有y甲﹣y乙=100×7﹣220﹣(80×7﹣100)=20千米<25千米,
∴按图象所表示的走法符合约定.
题型五、一次函数的综合题
1.(2022·山东聊城)如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A., B.,
C., D.,
【答案】C
【分析】作C(2,0)关于y轴的对称点G(2,0),作C(2,0)关于直线y=x+4的对称点D,连接AD,连接DG交AB于E,交y轴于F,此时△CEF周长最小,由y=x+4得A(-4,0),B(0,4),∠BAC=45°,根据C、D关于AB对称,可得D(-4,2),直线DG解析式为,即可得,由,得.
【详解】解:作关于轴的对称点,作关于直线的对称点D,连接AD,连接DG交AB于E,交轴于F,如图:
∴,,
∴,此时周长最小,
由得,,
∴,是等腰直角三角形,
∴,
∵C、D关于AB对称,
∴,
∴,
∵,
∴,
∴,
由,可得直线DG解析式为,
在中,令得,
∴,
由,得,
∴,
∴的坐标为,的坐标为,故选:C.
2.(2022·四川泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. B. C. D.
【答案】D
【分析】过点E作EG⊥AB于点G,利用三角函数求得EG=8,BG6,AG=4,再求得点E的坐标为(4,12),根据题意,直线l经过矩形OABC的对角线的交点H和菱形ABEF的对角线的交点D,根据中点坐标公式以及待定系数法即可求解.
【详解】解:过点E作EG⊥AB于点G,
∵矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,
∴AB=BE=10,点D的坐标为(0,4),点C的坐标为(10,0),
在Rt△BEG中,tan∠ABE=,BE=10,∴sin∠ABE=,即,
∴EG=8,BG=6,∴AG=4,∴点E的坐标为(4,12),
根据题意,直线l经过矩形OABC的对角线的交点H和菱形ABEF的对角线的交点D,
点H的坐标为(,),点D的坐标为(,),
∴点H的坐标为(5,2),点D的坐标为(2,8),设直线l的解析式为y=kx+b,
把(5,2),(2,8)代入得,解得:,
∴直线l的解析式为y=-2x+12,故选:D.
3.(2020·江苏南通)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
【答案】(1)y=﹣2x+6;(2)M(3,6)或(﹣1,2).
【解析】
【分析】
(1)把点C的坐标代入y=x+3,求出m的值,然后利用待定系数法求出直线的解析式;
(2)由已知条件得出M、N两点的横坐标,利用两点间距离公式求出M的坐标.
【详解】
解:(1)在y=x+3中,令y=0,得x=﹣3,
∴B(﹣3,0),
把x=1代入y=x+3得y=4,
∴C(1,4),
设直线l2的解析式为y=kx+b,
∴,解得,
∴直线l2的解析式为y=﹣2x+6;
(2)AB=3﹣(﹣3)=6,
设M(a,a+3),由MN∥y轴,得N(a,﹣2a+6),
MN=|a+3﹣(﹣2a+6)|=AB=6,
解得a=3或a=﹣1,
∴M(3,6)或(﹣1,2).
4.(2021·西藏)已知第一象限点P(x,y)在直线y=﹣x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
(2)当S=4时,求点P的坐标;
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
【答案】(1)6;(2)(3,2);(3)S=﹣2x+10(0<x<5),图见解析.
【解析】
【分析】
(1)求出点P坐标,再根据三角形面积公式进行计算即可;
(2)当S=4时求出点P的纵坐标,进而确定其横坐标;
(3)根据三角形的面积计算方法以及一次函数关系式得出答案.
【详解】
解:(1)把点P的横坐标为2代入得,y=﹣2+5=3,
∴点P(2,3),
∵点A的坐标为(4,0),
∴,
∴S△AOP=×4×3=6;
(2)当S=4时,即×4×y=4,
∴y=2,
当y=2时,即2=﹣x+5,
解得x=3,
∴点P(3,2);
(3)由题意得,
S=OA y=2y=2(﹣x+5)=﹣2x+10,
当y>0时,即0<x<5时,S=2(﹣x+5)=﹣2x+10,
∴S关于x的函数解析式为S=﹣2x+10(0<x<5),画出的图象如图所示.
5.(2022·黑龙江牡丹江)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
【答案】(1)C(0,6).(2)y=x+6.(3)P1(4,3),P2()P3(),P4().
【详解】试题分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:(1)解方程x2-14x+48=0得x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0) 由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴解得,∴直线MN的解析式为y=-x+6
(3)
∵A(8,0),C(0,6)∴根据题意知B(8,6)
∵点P在直线MN y=-x+6上∴设P(a,--a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-a+6-6)2=64
解得,a=±,则P2(-,),P3(,)
③当PB=BC时,(a-8)2+(-a+6-6)2=64
解得,a=,则-a+6=-∴P4(,)
综上所述,符合条件的点P有:P1(4,3),P2(-,),P3(,),P4(,-)
考点:一次函数综合题.
模块三 函数
专题2 一次函数
一次函数与正比例函数 一次函数与正比例函数的定义 如果y=kx+b(k≠0),那么y叫x的一次函数,当b=0时,一次函数y=kx也叫正比例函数.正比例函数是一次函数的特例,具有一次函数的性质.
一次函数与正比例函数的关系 一次函数y=kx+b(k≠0)的图象是过点(0,b)与直线y=kx平行的一条直线。它可以由直线y=kx平移得到.它与x轴的交点为,与y轴的交点为(0,b).
一次函数的 图象与性质 |k|越大,直线越陡; k相等,直线平行; b决定直线与y轴的交点(0,b) k>0 k<0
直线从左 向右上升 直线从左 向右下降
增减性 y随x的增大而增大 y随x的增大而减少
平移 当b>0时,图象向上平移b个单位长度; 当b<0时,图象向下平移|b|个单位长度.
确定一次函数解析式 确定一次函数的解析式 第一步:设,设出一次函数的一般形式y=kx+b(k≠0). 第二步:代,将已知点坐标代入解析式得出方程或方程组. 第三步:求,通过列方程或方程组求出待定系数k,b的值. 第四步:写,写出该函数的解析式.
与一元一次 方程的关系 一次函数y=kx+b与x轴交点的横坐标-是方程kx+b=0的解
与二元一次方程组的关系 一次函数y=kx+b与y=k1x+b1图象的交点坐标是方程组的解;反之,方程组的解是一次函数y=kx+b与y=k1x+b1图象的交点坐标
与一元一次不等式的关系 一次函数y=kx+b的函数值y>0时,自变量x的取值范围是kx+b>0的解集
一次函数y=kx+b的函数值y<0时,自变量x的取值范围是kx+b<0的解集
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
题型一、一次函数的概念与解析式
1.(2022·江苏泰州)一次函数的图像经过点(1,0).当y>0时,x的取值范围是__________.
2.(2022·湖南永州)已知一次函数的图象经过点,则______.
3.(2022 北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(-2,0),且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.
题型二、一次函数的图像与性质
1.(2022·内蒙古包头)在一次函数中,y的值随x值的增大而增大,且,则点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.(2022·四川广安)在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )
A.y=3x+5 B.y=3x﹣5 C.y=3x+1 D.y=3x﹣1
3.(2022·贵州遵义)若一次函数的函数值随的增大而减小,则值可能是( )
A.2 B. C. D.
4.(2022·辽宁锦州)点在一次函数的图像上,当时,,则a的取值范围是____________.
5.(2022·四川眉山)一次函数的值随的增大而增大,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022·湖南株洲)在平面直角坐标系中,一次函数的图象与轴的交点的坐标为( )
A. B. C. D.
7.(2022·湖南娄底)将直线向上平移2个单位,相当于( )
A.向左平移2个单位 B.向左平移1个单位 C.向右平移2个单位 D.向右平移1个单位
8.(2022·湖南邵阳)在直角坐标系中,已知点,点是直线上的两点,则,的大小关系是( )
A. B. C. D.
9.(2022·安徽)在同一平面直角坐标系中,一次函数与的图像可能是( )
A. B.C. D.
10.(2022·四川凉山)一次函数y=3x+b(b≥0)的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
题型三、一次函数与方程、不等式的关系
1.(2022·广西梧州)如图,在平面直角坐标系中,直线与直线相交于点A,则关于x,y的二元一次方程组的解是( )
A. B. C. D.
2.(2022·湖北鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
A.x>3 B.x<3 C.x<1 D.x>1
3.(2022·陕西)在同一平面直角坐标系中,直线与相交于点,则关于x,y的方程组的解为( )
A. B. C. D.
4.(2022·江苏扬州)如图,函数的图像经过点,则关于的不等式的解集为________.
5.(2022·浙江杭州)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组的解是_________.
题型四、一次函数的实际问题
1.(2022·内蒙古包头)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)求第14天小颖家草莓的日销售量;
(2)求当时,草莓价格m与x之间的函数关系式;
(3)试比较第8天与第10天的销售金额哪天多?
2.(2022·吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温(℃)与加热时间之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
(1)加热前水温是 ℃;
(2)求乙壶中水温关于加热时间的函数解析式;
(3)当甲壶中水温刚达到80℃时,乙壶中水温是 ℃.
3.(2022·浙江湖州)某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?
(2)如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;
(3)假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.
4.(2022·黑龙江牡丹江)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
(1)由于汽车发生故障,甲组在途中停留了___小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
题型五、一次函数的综合题
1.(2022·山东聊城)如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A., B.,
C., D.,
2.(2022·四川泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. B. C. D.
3.(2020·江苏南通)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
4.(2021·西藏)已知第一象限点P(x,y)在直线y=﹣x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
(2)当S=4时,求点P的坐标;
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
5.(2022·黑龙江牡丹江)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
2023年中考数学第一轮复习
模块三 函数
专题2 一次函数
知识梳理
一次函数与正比例函数 一次函数与正比例函数的定义 如果y=kx+b(k≠0),那么y叫x的一次函数,当b=0时,一次函数y=kx也叫正比例函数.正比例函数是一次函数的特例,具有一次函数的性质.
一次函数与正比例函数的关系 一次函数y=kx+b(k≠0)的图象是过点(0,b)与直线y=kx平行的一条直线。它可以由直线y=kx平移得到.它与x轴的交点为,与y轴的交点为(0,b).
一次函数的 图象与性质 |k|越大,直线越陡; k相等,直线平行; b决定直线与y轴的交点(0,b) k>0 k<0
直线从左 向右上升 直线从左 向右下降
增减性 y随x的增大而增大 y随x的增大而减少
平移 当b>0时,图象向上平移b个单位长度; 当b<0时,图象向下平移|b|个单位长度.
确定一次函数解析式 确定一次函数的解析式 第一步:设,设出一次函数的一般形式y=kx+b(k≠0). 第二步:代,将已知点坐标代入解析式得出方程或方程组. 第三步:求,通过列方程或方程组求出待定系数k,b的值. 第四步:写,写出该函数的解析式.
与一元一次 方程的关系 一次函数y=kx+b与x轴交点的横坐标-是方程kx+b=0的解
与二元一次方程组的关系 一次函数y=kx+b与y=k1x+b1图象的交点坐标是方程组的解;反之,方程组的解是一次函数y=kx+b与y=k1x+b1图象的交点坐标
与一元一次不等式的关系 一次函数y=kx+b的函数值y>0时,自变量x的取值范围是kx+b>0的解集
一次函数y=kx+b的函数值y<0时,自变量x的取值范围是kx+b<0的解集
题型梳理
题型一、一次函数的概念与解析式
1.(2022·江苏泰州)一次函数的图像经过点(1,0).当y>0时,x的取值范围是__________.
【答案】x<1
【分析】先用待定系数法,求出a的值.当y>0时,用含x的代数式表示y,解不等式即可.
【详解】解:把(1,0)代入一次函数,得
a+2=0,
解得:a=-2,
∴,
当y>0时,即,
解得:x<1.
故答案为:x<1.
2.(2022·湖南永州)已知一次函数的图象经过点,则______.
【答案】1
【分析】把点(m,2)代入一次函数y=x+1,列出关于m的一元一次方程,解之即可得m的值.
【详解】解:∵一次函数y=x+1的图象经过点(m,2)
∴把点(m,2)代入一次函数,得
m+1=2
解得:m=1
故答案为:1.
3.(2022 北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(-2,0),且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.
题型二、一次函数的图像与性质
1.(2022·内蒙古包头)在一次函数中,y的值随x值的增大而增大,且,则点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
【答案】B
【分析】根据一次函数的性质求出a的范围,再根据每个象限点的坐标特征判断A点所处的象限即可.
【详解】∵在一次函数中,y的值随x值的增大而增大,∴,即,
又∵,∴,∴点在第三象限,故选:B
2.(2022·四川广安)在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )
A.y=3x+5 B.y=3x﹣5 C.y=3x+1 D.y=3x﹣1
【答案】D
【分析】根据“上加下减,左加右减”的平移规律即可求解.
【详解】解:将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是y=3x﹣1,
故选:D
3.(2022·贵州遵义)若一次函数的函数值随的增大而减小,则值可能是( )
A.2 B. C. D.
【答案】D
【分析】根据一次函数的性质可得,即可求解.
【详解】解:∵一次函数的函数值随的增大而减小,
∴.
解得.
故选D.
4.(2022·辽宁锦州)点在一次函数的图像上,当时,,则a的取值范围是____________.
【答案】a<2
【分析】根据一次函数的性质,建立不等式计算即可.
【详解】∵当时,,
∴a-2<0,
∴a<2,
故答案为:a<2.
5.(2022·四川眉山)一次函数的值随的增大而增大,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】根据一次函数的性质求出m的范围,再根据每个象限点的坐标特征判断P点所处的象限即可.
【详解】∵一次函数的值随的增大而增大,
∴解得:∴在第二象限故选:B
6.(2022·湖南株洲)在平面直角坐标系中,一次函数的图象与轴的交点的坐标为( )
A. B. C. D.
【答案】D
【分析】令x=0,求出函数值,即可求解.
【详解】解:令x=0, ,
∴一次函数的图象与轴的交点的坐标为.故选:D
7.(2022·湖南娄底)将直线向上平移2个单位,相当于( )
A.向左平移2个单位 B.向左平移1个单位 C.向右平移2个单位 D.向右平移1个单位
【答案】B
【分析】函数图象的平移规律:左加右减,上加下减,根据规律逐一分析即可得到答案.
【详解】解:将直线向上平移2个单位,可得函数解析式为:
直线向左平移2个单位,可得 故A不符合题意;
直线向左平移1个单位,可得 故B符合题意;
直线向右平移2个单位,可得 故C不符合题意;
直线向右平移1个单位,可得 故D不符合题意;故选B
8.(2022·湖南邵阳)在直角坐标系中,已知点,点是直线上的两点,则,的大小关系是( )
A. B. C. D.
【答案】A
【分析】因为直线,所以随着自变量的增大,函数值会减小,根据这点即可得到问题解答.
【详解】解:∵因为直线,∴y随着x的增大而减小,
∵32>,∴∴m
A. B.C. D.
【答案】D
【分析】分为和两种情况,利用一次函数图像的性质进行判断即可.
【详解】解:当时,两个函数的函数值:,即两个图像都过点,故选项A、C不符合题意;
当时,,一次函数经过一、二、三象限,一次函数经过一、二、三象限,都与轴正半轴有交点,故选项B不符合题意;
当时,,一次函数经过一、二、四象限,与轴正半轴有交点,一次函数经过一、三、四象限,与轴负半轴有交点,故选项D符合题意.故选:D.
10.(2022·四川凉山)一次函数y=3x+b(b≥0)的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【分析】根据一次函数的性质可得其经过的象限,进而可得答案.
【详解】解:一次函数,
∵∴图象一定经过一、三象限,
∴当时,函数图象一定经过一、二、三象限,
当时,函数图象经过一、三象限,
∴函数图象一定不经过第四象限,故D正确.故选:D.
题型三、一次函数与方程、不等式的关系
1.(2022·广西梧州)如图,在平面直角坐标系中,直线与直线相交于点A,则关于x,y的二元一次方程组的解是( )
A. B. C. D.
【答案】B
【分析】由图象交点坐标可得方程组的解.
【详解】解:由图象可得直线与直线相交于点A(1,3),
∴关于x,y的二元一次方程组的解是.故选:B.
2.(2022·湖北鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
A.x>3 B.x<3 C.x<1 D.x>1
【答案】A
【分析】根据不等式kx+b<x的解集即为一次函数图象在正比例函数图象下方的自变量的取值范围求解即可
【详解】解:由函数图象可知不等式kx+b<x的解集即为一次函数图象在正比例函数图象下方的自变量的取值范围,
∴当kx+b<x时,x的取值范围是,
故选A.
3.(2022·陕西)在同一平面直角坐标系中,直线与相交于点,则关于x,y的方程组的解为( )
A. B. C. D.
【答案】C
【分析】先把点P代入直线求出n,再根据二元一次方程组与一次函数的关系求解即可;
【详解】解:∵直线与直线交于点P(3,n),
∴,∴,∴,∴1=3×2+m,∴m=-5,
∴关于x,y的方程组的解;故选:C.
4.(2022·江苏扬州)如图,函数的图像经过点,则关于的不等式的解集为________.
【答案】
【分析】观察一次函数图象,可知当y>3时,x的取值范围是,则的解集亦同.
【详解】由一次函数图象得,当y>3时,,
则y=kx+b>3的解集是.
5.(2022·浙江杭州)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组的解是_________.
【答案】
【分析】根据一次函数的交点坐标即可确定以两个一次函数解析式组成的二元一次方程组的解.
【详解】解:∵一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),
∴联立y=3x-1与y=kx的方程组的解为:,
即的解为:,故答案为:.
题型四、一次函数的实际问题
1.(2022·内蒙古包头)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)求第14天小颖家草莓的日销售量;
(2)求当时,草莓价格m与x之间的函数关系式;
(3)试比较第8天与第10天的销售金额哪天多?
【答案】(1)40千克(2)(3)第10天的销售金额多
【分析】(1)把x=14代入求出y值即可;
(2)用待定系数法求解,设m与x之间的函数关系式为,把(4,24),(12,16)代入,求出k,b值即可求解;
(3)把x=8,x=10分别代入y=12x,求出y,再把x=8,x=10分别代入(2)问所求解析式求出m值,然后分别求出my值,比较即可求解.
(1)解:∵当时,,
∴当时,(千克).
∴第14天小颖家草莓的日销售量是40千克.
(2)解:当时,设草莓价格m与x之间的函数关系式为,
∵点在的图像上,
∴解得
∴函数关系式为.
(3)解:∵当时,,
∴当时,,
当时,.
∵当时,,
∴当时,,当时,.
∴第8天的销售金额为:(元),
第10天的销售金额为:(元).
∵,∴第10天的销售金额多.
2.(2022·吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温(℃)与加热时间之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
(1)加热前水温是 ℃;
(2)求乙壶中水温关于加热时间的函数解析式;
(3)当甲壶中水温刚达到80℃时,乙壶中水温是 ℃.
【答案】(1)20 (2) (3)65
【分析】(1)根据时,即可得;
(2)先判断出乙壶对应的函数图象经过点,再利用待定系数法即可得;
(3)先利用待定系数法求出甲壶中与的函数解析式,再求出时,的值,然后将的值代入乙壶中与的函数解析式即可得.
(1)解:由函数图象可知,当时,,
则加热前水温是,故答案为:20.
(2)解:因为甲壶比乙壶加热速度快,
所以乙壶对应的函数图象经过点,
设乙壶中水温关于加热时间的函数解析式为,
将点代入得:,解得,
则乙壶中水温关于加热时间的函数解析式为,
自变量x的取值范围是0≤x≤160.
(3)解:设甲壶中水温关于加热时间的函数解析式为,
将点代入得:,解得,
则甲壶中水温关于加热时间的函数解析式为,
当时,,解得,
将代入得:,
即当甲壶中水温刚达到时,乙壶中水温是,故答案为:65.
3.(2022·浙江湖州)某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?
(2)如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;
(3)假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.
【答案】(1)轿车出发后2小时追上大巴,此时,两车与学校相距120千米
(2)点B的坐标是,s=60t-60(3)小时
【分析】(1)设轿车行驶的时间为x小时,则大巴行驶的时间为小时,根据路程两车行驶的路程相等得到即可求解;
(2)由(1)中轿车行驶的时间求出点B的坐标是,进而求出直线AB的解析式;
(3)根据大巴车行驶路程与小轿车行驶路程相等即可得到,进而求出a的值
(1)解:设轿车行驶的时间为x小时,则大巴行驶的时间为小时.
根据题意,得:,
解得x=2.
则千米,
∴轿车出发后2小时追上大巴,此时,两车与学校相距120千米.
(2)解:∵轿车追上大巴时,大巴行驶了3小时,
∴点B的坐标是.
由题意,得点A的坐标为.
设AB所在直线的解析式为,
则:
解得k=60,b=-60.
∴AB所在直线的解析式为s=60t-60.
(3)解:由题意,得,
解得:,
故a的值为小时.
4.(2022·黑龙江牡丹江)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
(1)由于汽车发生故障,甲组在途中停留了___小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
【答案】(1)1.9(2)270(3)按图象所表示的走法符合约定,理由见解析
【分析】(1)由于线段AB与x轴平行,故自3时到4.9时这段时间内甲组停留在途中,所以停留的时间为1.9时.(2)观察图象可知点B的纵坐标就是甲组的汽车在排除故障时距出发点的路程的千米数,从而求得直线EF和直线BD的解析式,即可求出B点的坐标.(3)由图象可知:甲、乙两组第一次相遇后在B和D相距最远,在两点处时, ,分别同25比较即可.
(1)4.9-3=1.9小时;故答案为:1.9
(2)设直线EF的解析式为y乙=kx+b,
∵点E(1.25,0)、点F(7.25,480)均在直线EF上,
∴,解得.
∴直线EF的解析式是y乙=80x﹣100.
∵点C在直线EF上,且点C的横坐标为6,
∴点C的纵坐标为80×6﹣100=380.
∴点C的坐标是(6,380).
设直线BD的解析式为y甲=mx+n;
∵点C(6,380)、点D(7,480)在直线BD上,
∴,解得.
∴BD的解析式是y甲=100x﹣220.
∵B点在直线BD上且点B的横坐标为4.9,代入y甲得B(4.9,270),
∴甲组在排除故障时,距出发点的路程是270千米.
(3)符合约定.理由如下:
由图象可知:甲、乙两组第一次相遇后在B和D相距最远,
在点B处有y乙﹣y甲=80×4.9﹣100﹣(100×4.9﹣220)=22千米<25千米,
在点D有y甲﹣y乙=100×7﹣220﹣(80×7﹣100)=20千米<25千米,
∴按图象所表示的走法符合约定.
题型五、一次函数的综合题
1.(2022·山东聊城)如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A., B.,
C., D.,
【答案】C
【分析】作C(2,0)关于y轴的对称点G(2,0),作C(2,0)关于直线y=x+4的对称点D,连接AD,连接DG交AB于E,交y轴于F,此时△CEF周长最小,由y=x+4得A(-4,0),B(0,4),∠BAC=45°,根据C、D关于AB对称,可得D(-4,2),直线DG解析式为,即可得,由,得.
【详解】解:作关于轴的对称点,作关于直线的对称点D,连接AD,连接DG交AB于E,交轴于F,如图:
∴,,
∴,此时周长最小,
由得,,
∴,是等腰直角三角形,
∴,
∵C、D关于AB对称,
∴,
∴,
∵,
∴,
∴,
由,可得直线DG解析式为,
在中,令得,
∴,
由,得,
∴,
∴的坐标为,的坐标为,故选:C.
2.(2022·四川泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. B. C. D.
【答案】D
【分析】过点E作EG⊥AB于点G,利用三角函数求得EG=8,BG6,AG=4,再求得点E的坐标为(4,12),根据题意,直线l经过矩形OABC的对角线的交点H和菱形ABEF的对角线的交点D,根据中点坐标公式以及待定系数法即可求解.
【详解】解:过点E作EG⊥AB于点G,
∵矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,
∴AB=BE=10,点D的坐标为(0,4),点C的坐标为(10,0),
在Rt△BEG中,tan∠ABE=,BE=10,∴sin∠ABE=,即,
∴EG=8,BG=6,∴AG=4,∴点E的坐标为(4,12),
根据题意,直线l经过矩形OABC的对角线的交点H和菱形ABEF的对角线的交点D,
点H的坐标为(,),点D的坐标为(,),
∴点H的坐标为(5,2),点D的坐标为(2,8),设直线l的解析式为y=kx+b,
把(5,2),(2,8)代入得,解得:,
∴直线l的解析式为y=-2x+12,故选:D.
3.(2020·江苏南通)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
【答案】(1)y=﹣2x+6;(2)M(3,6)或(﹣1,2).
【解析】
【分析】
(1)把点C的坐标代入y=x+3,求出m的值,然后利用待定系数法求出直线的解析式;
(2)由已知条件得出M、N两点的横坐标,利用两点间距离公式求出M的坐标.
【详解】
解:(1)在y=x+3中,令y=0,得x=﹣3,
∴B(﹣3,0),
把x=1代入y=x+3得y=4,
∴C(1,4),
设直线l2的解析式为y=kx+b,
∴,解得,
∴直线l2的解析式为y=﹣2x+6;
(2)AB=3﹣(﹣3)=6,
设M(a,a+3),由MN∥y轴,得N(a,﹣2a+6),
MN=|a+3﹣(﹣2a+6)|=AB=6,
解得a=3或a=﹣1,
∴M(3,6)或(﹣1,2).
4.(2021·西藏)已知第一象限点P(x,y)在直线y=﹣x+5上,点A的坐标为(4,0),设△AOP的面积为S.
(1)当点P的横坐标为2时,求△AOP的面积;
(2)当S=4时,求点P的坐标;
(3)求S关于x的函数解析式,写出x的取值范围,并在图中画出函数S的图象.
【答案】(1)6;(2)(3,2);(3)S=﹣2x+10(0<x<5),图见解析.
【解析】
【分析】
(1)求出点P坐标,再根据三角形面积公式进行计算即可;
(2)当S=4时求出点P的纵坐标,进而确定其横坐标;
(3)根据三角形的面积计算方法以及一次函数关系式得出答案.
【详解】
解:(1)把点P的横坐标为2代入得,y=﹣2+5=3,
∴点P(2,3),
∵点A的坐标为(4,0),
∴,
∴S△AOP=×4×3=6;
(2)当S=4时,即×4×y=4,
∴y=2,
当y=2时,即2=﹣x+5,
解得x=3,
∴点P(3,2);
(3)由题意得,
S=OA y=2y=2(﹣x+5)=﹣2x+10,
当y>0时,即0<x<5时,S=2(﹣x+5)=﹣2x+10,
∴S关于x的函数解析式为S=﹣2x+10(0<x<5),画出的图象如图所示.
5.(2022·黑龙江牡丹江)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
【答案】(1)C(0,6).(2)y=x+6.(3)P1(4,3),P2()P3(),P4().
【详解】试题分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:(1)解方程x2-14x+48=0得x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0) 由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴解得,∴直线MN的解析式为y=-x+6
(3)
∵A(8,0),C(0,6)∴根据题意知B(8,6)
∵点P在直线MN y=-x+6上∴设P(a,--a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-a+6-6)2=64
解得,a=±,则P2(-,),P3(,)
③当PB=BC时,(a-8)2+(-a+6-6)2=64
解得,a=,则-a+6=-∴P4(,)
综上所述,符合条件的点P有:P1(4,3),P2(-,),P3(,),P4(,-)
考点:一次函数综合题.
同课章节目录
