高二上学期物理人教版(2019)选择性必修第一册 2.3 简谐运动的回复力和能量 课件 (共14张PPT)
文档属性
| 名称 | 高二上学期物理人教版(2019)选择性必修第一册 2.3 简谐运动的回复力和能量 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-27 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
天下熙熙,皆为利来;
天下攘攘,皆为利往。
——司马迁
那么简谐运动的来来往往,
是不是也有“力来力往”呢?
2.3 简谐运动的回复力和能量
一、简谐运动的回复力
2.方向:总是指向平衡位置
4.理解:回复力是按力的作用效果命名的(类似于向心力)受力分析不要多力哦
效果:总是把物体拉回到平衡位置。
1.定义:使振动物体回到平衡位置的力。
回复力与位移有什么样的定量关系呢?
3.大小:F= -kx 回复力位移大小成正比,与位移方向相反
弹簧振子回复力是谁提供的呢?
5.简谐运动第二种表述:如果质点所受的力与它偏离平衡位置的位移大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动.即回复力满足 F= -kx的运动就是简谐运动 。对一般的简谐运动,k不一定是劲度系数而是回复力与位移的比例系数。
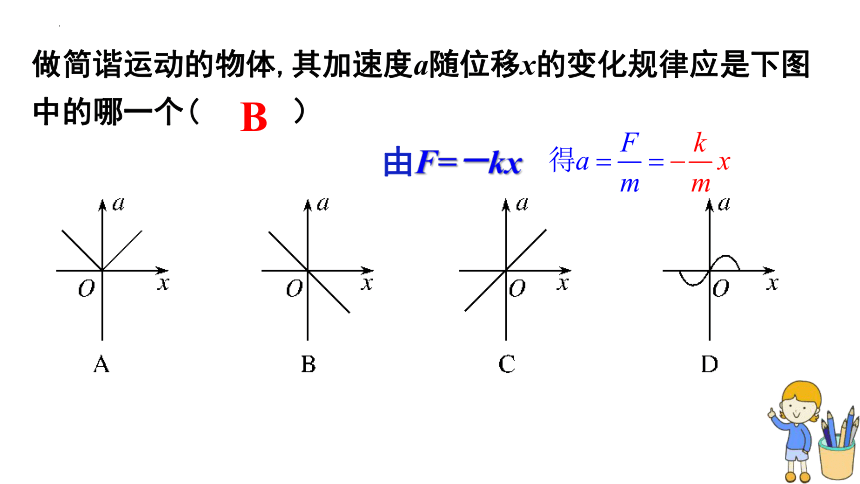
做简谐运动的物体,其加速度a随位移x的变化规律应是下图中的哪一个( )
B
由F=-kx
新课讲授
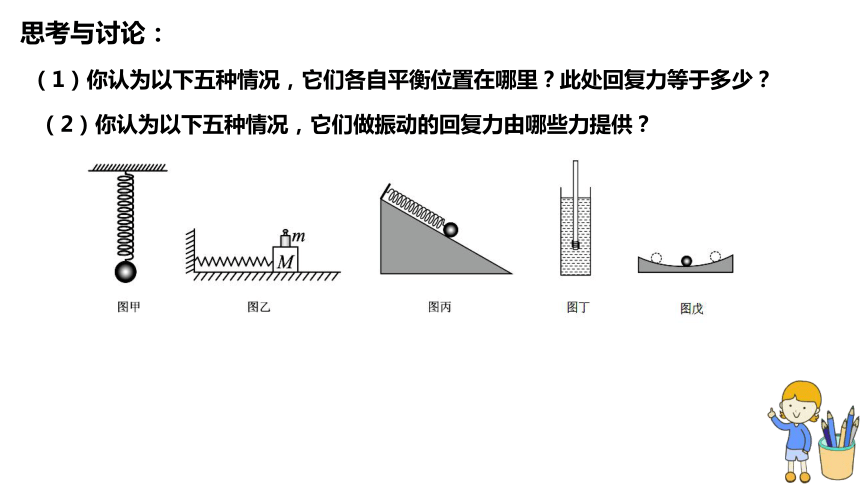
思考与讨论:
(1)你认为以下五种情况,它们各自平衡位置在哪里?此处回复力等于多少?
(2)你认为以下五种情况,它们做振动的回复力由哪些力提供?
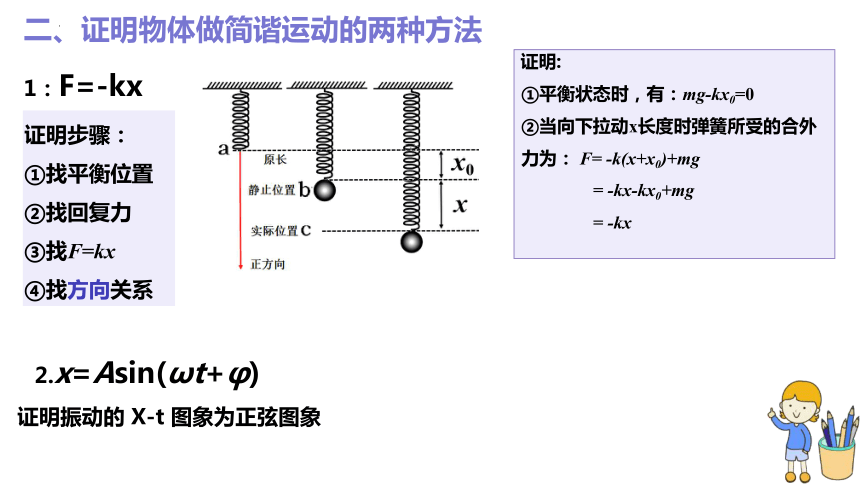
二、证明物体做简谐运动的两种方法
1:F=-kx
证明步骤:
①找平衡位置
②找回复力
③找F=kx
④找方向关系
证明振动的 X-t 图象为正弦图象
2.x=Asin(ωt+φ)
证明:
①平衡状态时,有:mg-kx0=0
②当向下拉动x长度时弹簧所受的合外力为: F= -k(x+x0)+mg
= -kx-kx0+mg
= -kx
D
三、简谐运动的能量
位置 Q Q→O O O→P P
位移的大小
速度的大小
动能
弹性势能
系统机械能
最大
↓
0
↑
最大
0
↑
最大
↓
0
0
↑
最大
↓
0
最大
↓
0
↑
最大
不变
不变
不变
不变
不变
O
P
Q
x
理解:
1.简谐运动中动能和势能相互转化,但机械能总量不变,即机械能守恒,是理想化模型。
2.简谐运动的能量与振幅有关,振幅越大,振动的能量越大。
3.物体在做简谐运动时的Ek-t和Ep-t及E-t图象
t
E
0
机械能
势能
动能
Q
P
O
1
如下图所示为一弹簧振子的振动图象,在下图中A、B、C、D、E、F各时刻中:
(1)哪些时刻振子有最大动能?(2)哪些时刻振子有相同速度?
(3)哪些时刻振子有最大势能?(4)哪些时刻振子有最大相同的加速度?
答案:
(1)B、D、F 时刻振子有最大动能
(2)A、C、E 时刻振子速度相同,B、F 时刻振子速度相同
(3)A、C、E 时刻振子有最大势能
(4)A、E 时刻有最大相同的加速度
解析:由图可知,B、D、F点在平衡位置,具有最大动能,而A、C、E点在最大位移处,具有最大势能。
根据振动方向:B、F两点向负方向振动,D点向正方向振动,可知D点与B、F点虽然速率相同,但方向相反。
根据位移:A、E两点位移相同,C点位移虽然大小与A、E两点相等,但方向相反可知C点与A、E点虽然受力相同,但方向相反,故加速度大小相等,方向相反。
C
课堂练习
如图所示,弹簧振子正在B、C之间做机械振动,当振子位于O点时弹簧为原长.在振子从C运动到O的过程中( )
A.速度不断增大,加速度不断增大
B.位移不断增大,加速度不断增大
C.速度不断增大,加速度不断减小
D.位移不断增大,加速度不断减小
C
天下熙熙,皆为利来;
天下攘攘,皆为利往。
——司马迁
那么简谐运动的来来往往,
是不是也有“力来力往”呢?
2.3 简谐运动的回复力和能量
一、简谐运动的回复力
2.方向:总是指向平衡位置
4.理解:回复力是按力的作用效果命名的(类似于向心力)受力分析不要多力哦
效果:总是把物体拉回到平衡位置。
1.定义:使振动物体回到平衡位置的力。
回复力与位移有什么样的定量关系呢?
3.大小:F= -kx 回复力位移大小成正比,与位移方向相反
弹簧振子回复力是谁提供的呢?
5.简谐运动第二种表述:如果质点所受的力与它偏离平衡位置的位移大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动.即回复力满足 F= -kx的运动就是简谐运动 。对一般的简谐运动,k不一定是劲度系数而是回复力与位移的比例系数。
做简谐运动的物体,其加速度a随位移x的变化规律应是下图中的哪一个( )
B
由F=-kx
新课讲授
思考与讨论:
(1)你认为以下五种情况,它们各自平衡位置在哪里?此处回复力等于多少?
(2)你认为以下五种情况,它们做振动的回复力由哪些力提供?
二、证明物体做简谐运动的两种方法
1:F=-kx
证明步骤:
①找平衡位置
②找回复力
③找F=kx
④找方向关系
证明振动的 X-t 图象为正弦图象
2.x=Asin(ωt+φ)
证明:
①平衡状态时,有:mg-kx0=0
②当向下拉动x长度时弹簧所受的合外力为: F= -k(x+x0)+mg
= -kx-kx0+mg
= -kx
D
三、简谐运动的能量
位置 Q Q→O O O→P P
位移的大小
速度的大小
动能
弹性势能
系统机械能
最大
↓
0
↑
最大
0
↑
最大
↓
0
0
↑
最大
↓
0
最大
↓
0
↑
最大
不变
不变
不变
不变
不变
O
P
Q
x
理解:
1.简谐运动中动能和势能相互转化,但机械能总量不变,即机械能守恒,是理想化模型。
2.简谐运动的能量与振幅有关,振幅越大,振动的能量越大。
3.物体在做简谐运动时的Ek-t和Ep-t及E-t图象
t
E
0
机械能
势能
动能
Q
P
O
1
如下图所示为一弹簧振子的振动图象,在下图中A、B、C、D、E、F各时刻中:
(1)哪些时刻振子有最大动能?(2)哪些时刻振子有相同速度?
(3)哪些时刻振子有最大势能?(4)哪些时刻振子有最大相同的加速度?
答案:
(1)B、D、F 时刻振子有最大动能
(2)A、C、E 时刻振子速度相同,B、F 时刻振子速度相同
(3)A、C、E 时刻振子有最大势能
(4)A、E 时刻有最大相同的加速度
解析:由图可知,B、D、F点在平衡位置,具有最大动能,而A、C、E点在最大位移处,具有最大势能。
根据振动方向:B、F两点向负方向振动,D点向正方向振动,可知D点与B、F点虽然速率相同,但方向相反。
根据位移:A、E两点位移相同,C点位移虽然大小与A、E两点相等,但方向相反可知C点与A、E点虽然受力相同,但方向相反,故加速度大小相等,方向相反。
C
课堂练习
如图所示,弹簧振子正在B、C之间做机械振动,当振子位于O点时弹簧为原长.在振子从C运动到O的过程中( )
A.速度不断增大,加速度不断增大
B.位移不断增大,加速度不断增大
C.速度不断增大,加速度不断减小
D.位移不断增大,加速度不断减小
C
