总复习 2 图形与测量(2)(课件)-六年级下册数学北师大版(共30张PPT)
文档属性
| 名称 | 总复习 2 图形与测量(2)(课件)-六年级下册数学北师大版(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
图形与几何
总复习
总复习
北师版·六年级下册
图形与测量(2)
数与代数
图形与几何
统计与概率
图形的认识
图形与测量
图形的运动
图形的位置
统计
可能性
综合与实践
解决问题的策略
数的认识
数的运算
式与方程
正比例与反比例
常见的量
探索规律
整数
小数、分数、百分数
运算的意义
计算与应用
估算
运算律
北师版小学数学
总复习
图形与测量
图形与几何
周长和面积
长度
表面积和体积
图形的认识
点
面
体
线
(一条)线
(两条)线(的位置关系)
多边形
圆
三角形
四边形
五边形
......
平行四边形
梯形
......
长方形
正方形
正方体
长方体
圆柱
圆锥
球
直线
曲线
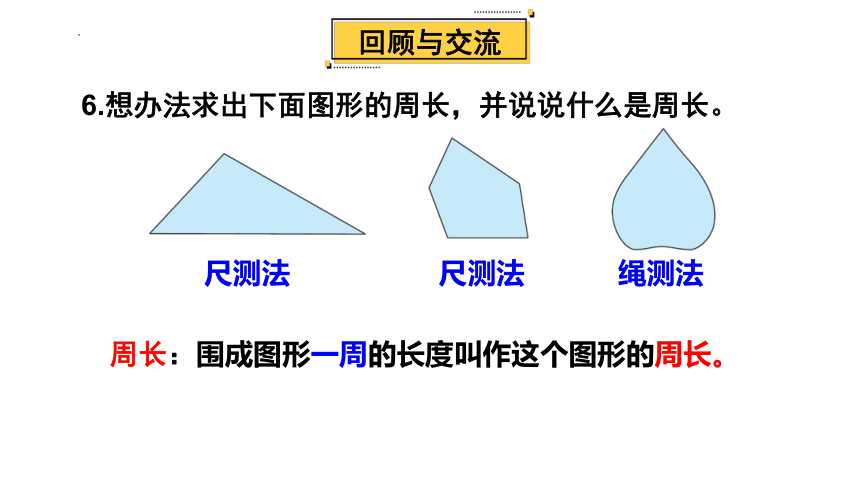
周长:围成图形一周的长度叫作这个图形的周长。
6.想办法求出下面图形的周长,并说说什么是周长。
尺测法
尺测法
绳测法
回顾与交流
6.想办法求出下面图形的周长,并说说什么是周长。
尺测法
尺测法
绳测法
正方形的周长:_____________
长方形的周长:_____________
圆的周长:_____________
C=4a
C=2a+2b
C=πd=2πr
回顾与交流
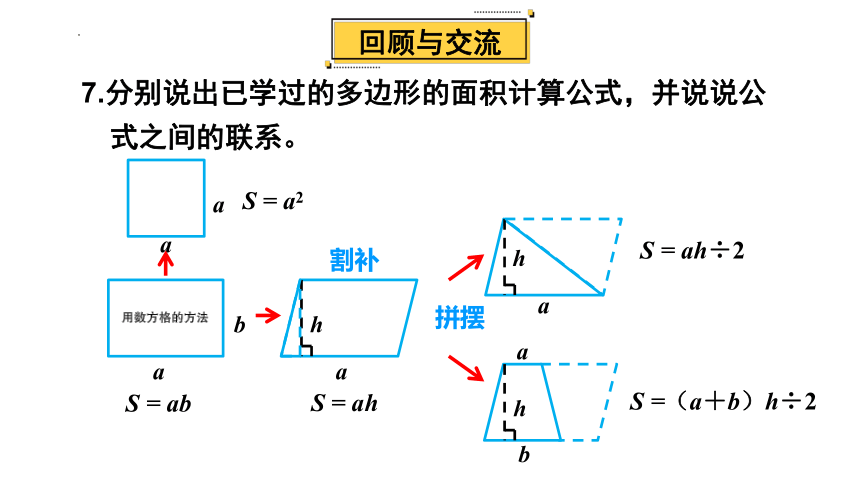
7.分别说出已学过的多边形的面积计算公式,并说说公
式之间的联系。
面积:物体的表面或围成的平面图形的大小,叫作它
的面积。
回顾与交流
7.分别说出已学过的多边形的面积计算公式,并说说公
式之间的联系。
a
b
a
h
a
h
b
h
a
割补
拼摆
S = ab
S = ah
S = ah÷2
S =(a+b)h÷2
a
a
S = a2
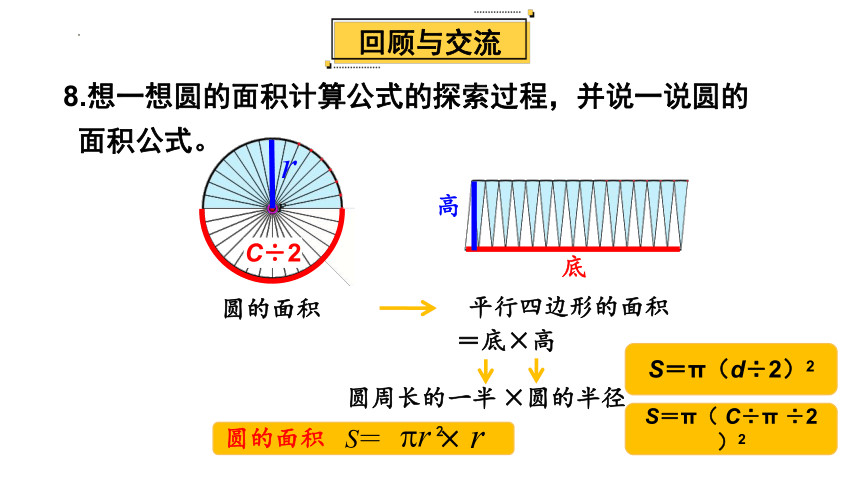
回顾与交流
C÷2
底
高
圆的面积
圆周长的一半
=底×高
平行四边形的面积
圆的半径
×
×
圆的面积
2
8.想一想圆的面积计算公式的探索过程,并说一说圆的
面积公式。
S=π(d÷2)2
S=π( C÷π ÷2)2
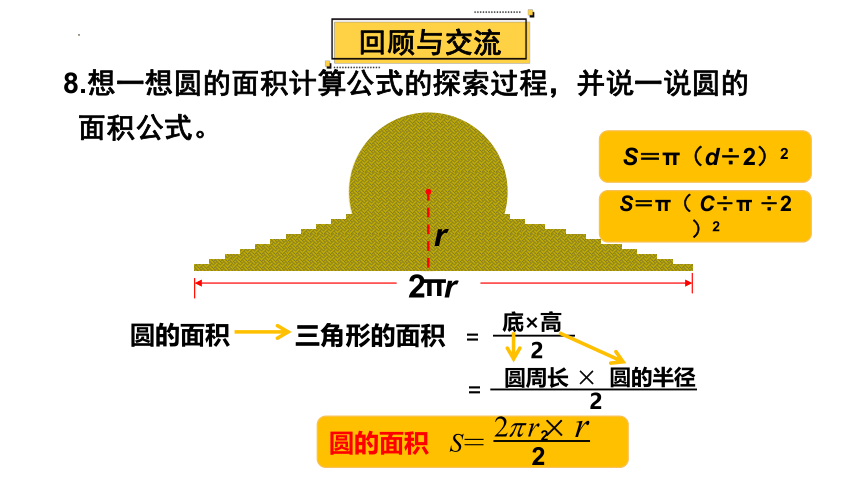
回顾与交流
8.想一想圆的面积计算公式的探索过程,并说一说圆的
面积公式。
2 r
π
r
圆的面积
三角形的面积
=
2
底×高
×
2
=
×
圆的面积
2
2
圆周长
圆的半径
S=π(d÷2)2
S=π( C÷π ÷2)2
回顾与交流
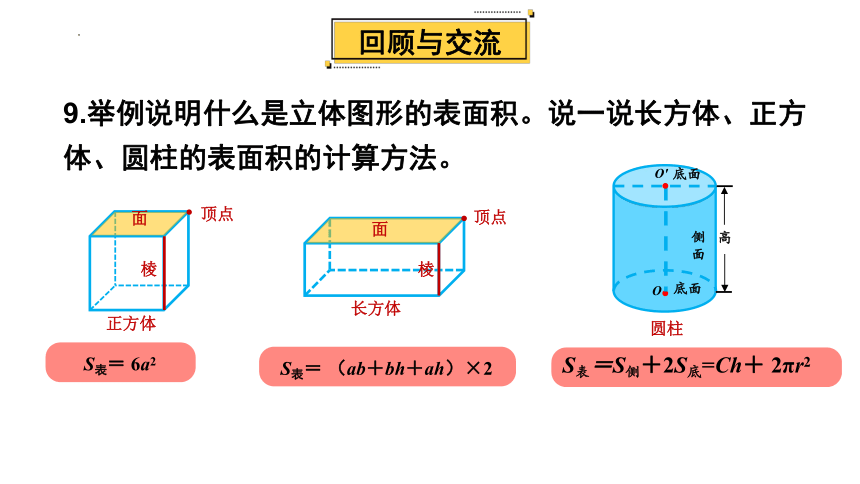
9.举例说明什么是立体图形的表面积。说一说长方体、正方体、圆柱的表面积的计算方法。
正方体
面
棱
顶点
S表= 6a2
长方体
面
棱
顶点
S表= (ab+bh+ah)×2
底面
底面
O
O'
侧面
高
圆柱
S表=S侧+2S底=Ch+ 2πr2
回顾与交流
9. 分别说出已学过的立体图形的体积计算公式,并说说公式之间的联系。
V = abh
V = Sh
V = a3
V = Sh
V锥 = Sh
a
b
a
h
S
h
h
S
回顾与交流
4.图形A,B,C的面积分别是多少平方厘米 图形D的面积大约是多少平方厘米 (每格面积表示1 cm2)
【选自教材P95 巩固与应用 】
5 cm2
6 cm2
2 cm2
9 cm2
巩固与应用
5. 如图,圆的周长是62.8 cm。正方形的周长是多少
62.8÷3.14=20(cm)
20×4=80(cm)
答:正方形的周长是80cm.
【选自教材P95 巩固与应用 】
5. 如图,圆的周长是62.8 cm。正方形的周长是多少
【选自教材P95 巩固与应用 】
6.求下面各图形中涂色部分的面积。
【选自教材P95 巩固与应用 】
(60+80)×30÷2-60×20÷2
=1500(dm2)
方法一:
7×4+(15-4)×(7-4)=61(dm2)
方法二:
4×4+15×(7-4)=61(dm2)
方法三:
15×7-(15-4)×4=61(dm2)
6.求下面各图形中涂色部分的面积。
【选自教材P95 巩固与应用 】
方法一:
方法二:
方法三:
7.
【选自教材P96 巩固与应用 】
(1)做上面两个无盖鱼缸,至少各需要多少平方厘米玻璃
长方体:60×40+40×50×2+60×50×2=12400(cm2)
正方体:50×50×5=12500(cm2)
7.
【选自教材P96 巩固与应用 】
(1)做上面两个无盖鱼缸,至少各需要多少平方厘米玻璃
7.
【选自教材P96 巩固与应用 】
(2)哪个鱼缸盛水多 先猜一猜,再计算多了多少升。
长方体鱼缸:60×40×50=120000(mL)=120(L)
正方体鱼缸:50×50×50=125000(mL)=125(L)
125-120=5(L)
所以正方体鱼缸盛水多,多5L。
7.
【选自教材P96 巩固与应用 】
(2)哪个鱼缸盛水多 先猜一猜,再计算多了多少升。
8.
【选自教材P96 巩固与应用 】
要包装100个圆柱形易拉罐的侧面,至少共需要多少平方分米的广告纸
3.14×6×12×100=22608(cm2)=226.08(dm2)
答:至少共需要226.08平方分米的广告纸。
8.
【选自教材P96 巩固与应用 】
要包装100个圆柱形易拉罐的侧面,至少共需要多少平方分米的广告纸
9.一圆锥形小麦堆的底面周长为15.7 m,高1.5 m。如果每立方米小麦的质量为700 kg,这堆小麦的质量约为多少千克
【选自教材P96 巩固与应用 】
15.7÷3.14÷2=2.5(m)
×3.14×2.52×1.5=9.8125(m3)
9.8125×700=6868.75(kg)
答:这堆小麦的质量约为6868.75 kg。
9.一圆锥形小麦堆的底面周长为15.7 m,高1.5 m。如果每立方米小麦的质量为700 kg,这堆小麦的质量约为多少千克
【选自教材P96 巩固与应用 】
10.用一根长48 dm的铁丝做一个长方体的框架,使它的高为8 dm,长、宽的比是1∶1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸
【选自教材P96 巩固与应用 】
48÷4=12(dm)
12-8=4(dm)
4× =2(dm)
表面积:2×8×4+2×2=68(dm2)
答:至少需要68 dm2的纸
10.用一根长48 dm的铁丝做一个长方体的框架,使它的高为8 dm,长、宽的比是1∶1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸
【选自教材P96 巩固与应用 】
11.用3个同样的小长方体,拼成一个大长方体,可能有几种情况 它们的表面积各是多少
【选自教材P96 巩固与应用 】
3
2
3
42
6
1
3
54
9
1
2
58
周长和面积
长度
表面积和体积
图形的认识
点
面
体
线
(一条)线
(两条)线(的位置关系)
多边形
圆
三角形
四边形
五边形
......
平行四边形
梯形
......
长方形
正方形
正方体
长方体
圆柱
圆锥
球
直线
曲线
课堂小结
完成练习册本课时的习题。
课后作业
图形与几何
总复习
总复习
北师版·六年级下册
图形与测量(2)
数与代数
图形与几何
统计与概率
图形的认识
图形与测量
图形的运动
图形的位置
统计
可能性
综合与实践
解决问题的策略
数的认识
数的运算
式与方程
正比例与反比例
常见的量
探索规律
整数
小数、分数、百分数
运算的意义
计算与应用
估算
运算律
北师版小学数学
总复习
图形与测量
图形与几何
周长和面积
长度
表面积和体积
图形的认识
点
面
体
线
(一条)线
(两条)线(的位置关系)
多边形
圆
三角形
四边形
五边形
......
平行四边形
梯形
......
长方形
正方形
正方体
长方体
圆柱
圆锥
球
直线
曲线
周长:围成图形一周的长度叫作这个图形的周长。
6.想办法求出下面图形的周长,并说说什么是周长。
尺测法
尺测法
绳测法
回顾与交流
6.想办法求出下面图形的周长,并说说什么是周长。
尺测法
尺测法
绳测法
正方形的周长:_____________
长方形的周长:_____________
圆的周长:_____________
C=4a
C=2a+2b
C=πd=2πr
回顾与交流
7.分别说出已学过的多边形的面积计算公式,并说说公
式之间的联系。
面积:物体的表面或围成的平面图形的大小,叫作它
的面积。
回顾与交流
7.分别说出已学过的多边形的面积计算公式,并说说公
式之间的联系。
a
b
a
h
a
h
b
h
a
割补
拼摆
S = ab
S = ah
S = ah÷2
S =(a+b)h÷2
a
a
S = a2
回顾与交流
C÷2
底
高
圆的面积
圆周长的一半
=底×高
平行四边形的面积
圆的半径
×
×
圆的面积
2
8.想一想圆的面积计算公式的探索过程,并说一说圆的
面积公式。
S=π(d÷2)2
S=π( C÷π ÷2)2
回顾与交流
8.想一想圆的面积计算公式的探索过程,并说一说圆的
面积公式。
2 r
π
r
圆的面积
三角形的面积
=
2
底×高
×
2
=
×
圆的面积
2
2
圆周长
圆的半径
S=π(d÷2)2
S=π( C÷π ÷2)2
回顾与交流
9.举例说明什么是立体图形的表面积。说一说长方体、正方体、圆柱的表面积的计算方法。
正方体
面
棱
顶点
S表= 6a2
长方体
面
棱
顶点
S表= (ab+bh+ah)×2
底面
底面
O
O'
侧面
高
圆柱
S表=S侧+2S底=Ch+ 2πr2
回顾与交流
9. 分别说出已学过的立体图形的体积计算公式,并说说公式之间的联系。
V = abh
V = Sh
V = a3
V = Sh
V锥 = Sh
a
b
a
h
S
h
h
S
回顾与交流
4.图形A,B,C的面积分别是多少平方厘米 图形D的面积大约是多少平方厘米 (每格面积表示1 cm2)
【选自教材P95 巩固与应用 】
5 cm2
6 cm2
2 cm2
9 cm2
巩固与应用
5. 如图,圆的周长是62.8 cm。正方形的周长是多少
62.8÷3.14=20(cm)
20×4=80(cm)
答:正方形的周长是80cm.
【选自教材P95 巩固与应用 】
5. 如图,圆的周长是62.8 cm。正方形的周长是多少
【选自教材P95 巩固与应用 】
6.求下面各图形中涂色部分的面积。
【选自教材P95 巩固与应用 】
(60+80)×30÷2-60×20÷2
=1500(dm2)
方法一:
7×4+(15-4)×(7-4)=61(dm2)
方法二:
4×4+15×(7-4)=61(dm2)
方法三:
15×7-(15-4)×4=61(dm2)
6.求下面各图形中涂色部分的面积。
【选自教材P95 巩固与应用 】
方法一:
方法二:
方法三:
7.
【选自教材P96 巩固与应用 】
(1)做上面两个无盖鱼缸,至少各需要多少平方厘米玻璃
长方体:60×40+40×50×2+60×50×2=12400(cm2)
正方体:50×50×5=12500(cm2)
7.
【选自教材P96 巩固与应用 】
(1)做上面两个无盖鱼缸,至少各需要多少平方厘米玻璃
7.
【选自教材P96 巩固与应用 】
(2)哪个鱼缸盛水多 先猜一猜,再计算多了多少升。
长方体鱼缸:60×40×50=120000(mL)=120(L)
正方体鱼缸:50×50×50=125000(mL)=125(L)
125-120=5(L)
所以正方体鱼缸盛水多,多5L。
7.
【选自教材P96 巩固与应用 】
(2)哪个鱼缸盛水多 先猜一猜,再计算多了多少升。
8.
【选自教材P96 巩固与应用 】
要包装100个圆柱形易拉罐的侧面,至少共需要多少平方分米的广告纸
3.14×6×12×100=22608(cm2)=226.08(dm2)
答:至少共需要226.08平方分米的广告纸。
8.
【选自教材P96 巩固与应用 】
要包装100个圆柱形易拉罐的侧面,至少共需要多少平方分米的广告纸
9.一圆锥形小麦堆的底面周长为15.7 m,高1.5 m。如果每立方米小麦的质量为700 kg,这堆小麦的质量约为多少千克
【选自教材P96 巩固与应用 】
15.7÷3.14÷2=2.5(m)
×3.14×2.52×1.5=9.8125(m3)
9.8125×700=6868.75(kg)
答:这堆小麦的质量约为6868.75 kg。
9.一圆锥形小麦堆的底面周长为15.7 m,高1.5 m。如果每立方米小麦的质量为700 kg,这堆小麦的质量约为多少千克
【选自教材P96 巩固与应用 】
10.用一根长48 dm的铁丝做一个长方体的框架,使它的高为8 dm,长、宽的比是1∶1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸
【选自教材P96 巩固与应用 】
48÷4=12(dm)
12-8=4(dm)
4× =2(dm)
表面积:2×8×4+2×2=68(dm2)
答:至少需要68 dm2的纸
10.用一根长48 dm的铁丝做一个长方体的框架,使它的高为8 dm,长、宽的比是1∶1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸
【选自教材P96 巩固与应用 】
11.用3个同样的小长方体,拼成一个大长方体,可能有几种情况 它们的表面积各是多少
【选自教材P96 巩固与应用 】
3
2
3
42
6
1
3
54
9
1
2
58
周长和面积
长度
表面积和体积
图形的认识
点
面
体
线
(一条)线
(两条)线(的位置关系)
多边形
圆
三角形
四边形
五边形
......
平行四边形
梯形
......
长方形
正方形
正方体
长方体
圆柱
圆锥
球
直线
曲线
课堂小结
完成练习册本课时的习题。
课后作业
