5.3.2.1函数的极值 课件(共16张PPT)
文档属性
| 名称 | 5.3.2.1函数的极值 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-27 21:21:58 | ||
图片预览





文档简介
5.3.2.1函数的极值
李若男
1、导数的几何意义是什么?
切线的斜率
2、如何利用导数研究函数的单调性?
(1)在某个区间(a,b)内,若f′(x)>0,则f(x)在(a,b)上是增函数。
(2)在某个区间(a,b)内,若f′(x)<0,则f(x)在(a,b)上是减函数。
复习巩固
情境导入
这是江西庐山群山叠嶂的景象。苏轼在《题西林壁》中这样写道:“横看成岭侧成峰,远近高低各不同”,描述的就是庐山的高低起伏,错落有致。在群山之中,各个山峰的顶端,虽然不是群山的最高处,但它却是其附近的最高点。
那么,在数学上,这种现象如何来刻画呢?
情境导入
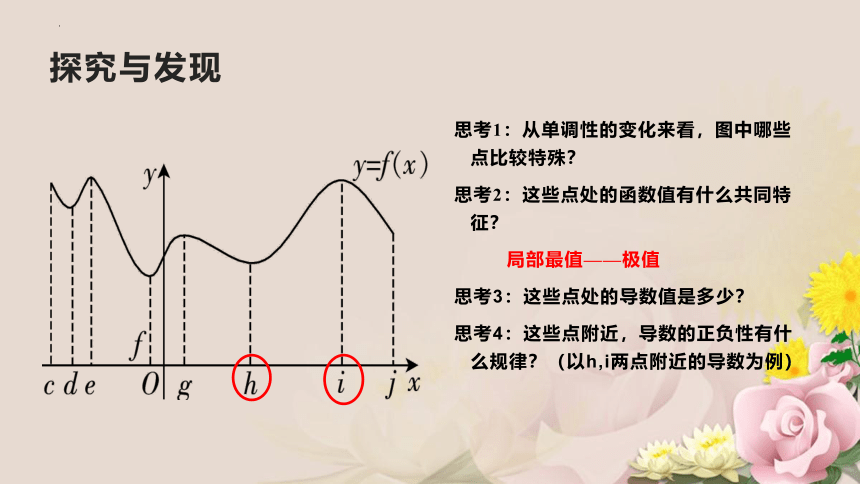
思考1:从单调性的变化来看,图中哪些 点比较特殊?
思考2:这些点处的函数值有什么共同特征?
局部最值——极值
思考3:这些点处的导数值是多少?
思考4:这些点附近,导数的正负性有什 么规律?(以h,i两点附近的导数为例)
探究与发现
概念生成
如图,函数 ????=???????? 在点 ????=???? 的函数值 ???????? 比它在点 ????=???? 附近其他点的函数值都小, ????′????=???? ;而且在点 ????=???? 附近的左侧 ????′???????? ,则把点 ????=???? 叫作函数 ????=???????? 的极小值点, ???????? 叫作函数 ????=???????? 的极小值.
函数 ????=???????? 在点 ????=???? 的函数值 ???????? 比它在点 ????=???? 附近其他点的函数值都大, ????′????=???? ;而且在点 ????=???? 附近的左侧 ????′????>???? ,右侧 ????′?????
概念生成
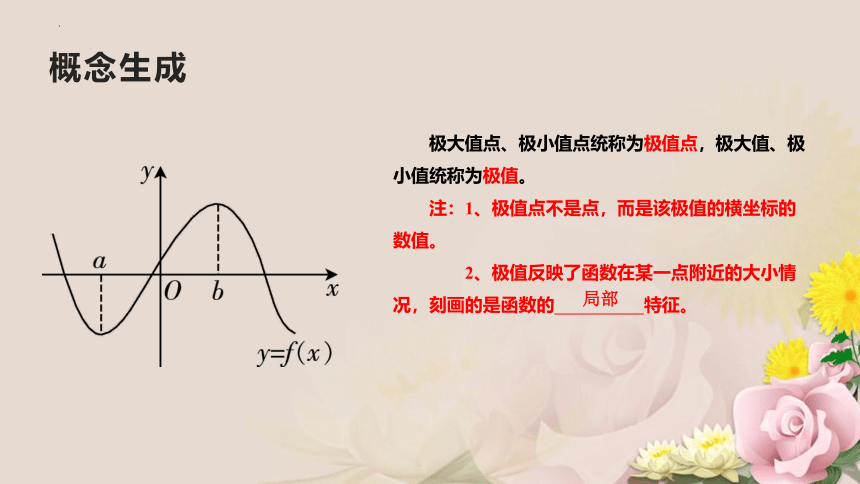
极大值点、极小值点统称为极值点,极大值、极小值统称为极值。
注:1、极值点不是点,而是该极值的横坐标的数值。
2、极值反映了函数在某一点附近的大小情况,刻画的是函数的 特征。
局部
概念巩固
问题1:极大值点是 。
极大值是 。
极小值点是 。
极小值是 。
问题2:极大值一定大于极小值吗?
不一定。极大值和极小值没有必然的联系(局部性质)。
问题3:函数的极值唯一吗?
不唯一。可能有多个,可能不存在。
e、g、i
f(e)、f(g)、f(i)
d、f、h
f(d)、f(f)、f(h)
概念应用
例1、判断下列函数是否有极值,如果有,说出是极大值还是极小值。
1、????????=2
2、????????=x
3、????????=-x2+3x-5
4、????????=sinx
?
无极值
无极值
有极大值
有极大值和极小值
例题讲解
例2、求函数????????=????????x3-x+4的极值。
?
概念理解
a
b
左减右增极小值
左增右减极大值
左负右正极小值
左正右负极大值
????′????=????
?
????′????=????
?
例题讲解
例2、求函数????????=????????x3-x+4的极值。
?
概念巩固
练习:求函数 y=3x3-x+1的极值。
[解析] y′=9x2?1 ,令 y′=0 ,解得 x1=13 , x2=?13 .
当 x 变化时, y′ 和 y 的变化情况如表所示:
?
x
?∞,?13
?13
?13,13
13
13,+∞
y′
+
0
-
0
+
y
↗
极大值
↘
极小值
↗
因此,当 x=?13 时, y 有极大值,极大值为 119 ;
当 x=13 时, y 有极小值,极小值为 79 .
?
方法总结
1、图像法判断函数的极值
2、概念法判断函数的极值:
(1)确定函数的定义域,求导数 ????′???? ;
(2)求方程 ????′????=???? 的根;
(3)用函数的导数为0的点,顺次将函数的定义域分成若干个小开区间,并列成表格.检测 ????′???? 在方程根左、右两侧的值的符号,如果左正右负,那么 ???????? 在这个根处取得极大值;如果左负右正,那么 ???????? 在这个根处取得极小值;如果左、右不改变符号,那么 ???????? 在这个根处无极值.
?
课后作业
1、思考:p:可导函数y=f(x)在a点处取得极值 q:????′????=0
p是q的什么条件?
2、课时作业(十九)1,2,3,6,9
?
谢谢观看!
李若男
1、导数的几何意义是什么?
切线的斜率
2、如何利用导数研究函数的单调性?
(1)在某个区间(a,b)内,若f′(x)>0,则f(x)在(a,b)上是增函数。
(2)在某个区间(a,b)内,若f′(x)<0,则f(x)在(a,b)上是减函数。
复习巩固
情境导入
这是江西庐山群山叠嶂的景象。苏轼在《题西林壁》中这样写道:“横看成岭侧成峰,远近高低各不同”,描述的就是庐山的高低起伏,错落有致。在群山之中,各个山峰的顶端,虽然不是群山的最高处,但它却是其附近的最高点。
那么,在数学上,这种现象如何来刻画呢?
情境导入
思考1:从单调性的变化来看,图中哪些 点比较特殊?
思考2:这些点处的函数值有什么共同特征?
局部最值——极值
思考3:这些点处的导数值是多少?
思考4:这些点附近,导数的正负性有什 么规律?(以h,i两点附近的导数为例)
探究与发现
概念生成
如图,函数 ????=???????? 在点 ????=???? 的函数值 ???????? 比它在点 ????=???? 附近其他点的函数值都小, ????′????=???? ;而且在点 ????=???? 附近的左侧 ????′???????? ,则把点 ????=???? 叫作函数 ????=???????? 的极小值点, ???????? 叫作函数 ????=???????? 的极小值.
函数 ????=???????? 在点 ????=???? 的函数值 ???????? 比它在点 ????=???? 附近其他点的函数值都大, ????′????=???? ;而且在点 ????=???? 附近的左侧 ????′????>???? ,右侧 ????′?????
概念生成
极大值点、极小值点统称为极值点,极大值、极小值统称为极值。
注:1、极值点不是点,而是该极值的横坐标的数值。
2、极值反映了函数在某一点附近的大小情况,刻画的是函数的 特征。
局部
概念巩固
问题1:极大值点是 。
极大值是 。
极小值点是 。
极小值是 。
问题2:极大值一定大于极小值吗?
不一定。极大值和极小值没有必然的联系(局部性质)。
问题3:函数的极值唯一吗?
不唯一。可能有多个,可能不存在。
e、g、i
f(e)、f(g)、f(i)
d、f、h
f(d)、f(f)、f(h)
概念应用
例1、判断下列函数是否有极值,如果有,说出是极大值还是极小值。
1、????????=2
2、????????=x
3、????????=-x2+3x-5
4、????????=sinx
?
无极值
无极值
有极大值
有极大值和极小值
例题讲解
例2、求函数????????=????????x3-x+4的极值。
?
概念理解
a
b
左减右增极小值
左增右减极大值
左负右正极小值
左正右负极大值
????′????=????
?
????′????=????
?
例题讲解
例2、求函数????????=????????x3-x+4的极值。
?
概念巩固
练习:求函数 y=3x3-x+1的极值。
[解析] y′=9x2?1 ,令 y′=0 ,解得 x1=13 , x2=?13 .
当 x 变化时, y′ 和 y 的变化情况如表所示:
?
x
?∞,?13
?13
?13,13
13
13,+∞
y′
+
0
-
0
+
y
↗
极大值
↘
极小值
↗
因此,当 x=?13 时, y 有极大值,极大值为 119 ;
当 x=13 时, y 有极小值,极小值为 79 .
?
方法总结
1、图像法判断函数的极值
2、概念法判断函数的极值:
(1)确定函数的定义域,求导数 ????′???? ;
(2)求方程 ????′????=???? 的根;
(3)用函数的导数为0的点,顺次将函数的定义域分成若干个小开区间,并列成表格.检测 ????′???? 在方程根左、右两侧的值的符号,如果左正右负,那么 ???????? 在这个根处取得极大值;如果左负右正,那么 ???????? 在这个根处取得极小值;如果左、右不改变符号,那么 ???????? 在这个根处无极值.
?
课后作业
1、思考:p:可导函数y=f(x)在a点处取得极值 q:????′????=0
p是q的什么条件?
2、课时作业(十九)1,2,3,6,9
?
谢谢观看!
