7.3.1万有引力理论的成就 计算质量和密度、黄金代换 课件(18张PPT)-物理人教版(2019)必修第二册
文档属性
| 名称 | 7.3.1万有引力理论的成就 计算质量和密度、黄金代换 课件(18张PPT)-物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-27 23:19:17 | ||
图片预览





文档简介
§7.31 万有引力理论的成就
(计算质量和密度、黄金代换)
第七章 万有引力与宇宙航行
课前练.( 2014·海南·高考真题)设地球自转周期为T,质量为M,引力常量为G。假设地球可视为质量均匀分布的球体,半径为R 。同一物体在南极和赤道水平面上静止时所受到的支持力之比为( )
A.????????????????????????????????????????????????????? B.????????????????????????????????+????????????????????
C.????????????????????????????????????????????????????? D.????????????????+????????????????????????????????????
?
A
一、“称量”地球的质量
在初中,我们已经知道物体的质量可以用天平来测量。对于地球,我们怎样“称量”它的质量呢?
已知地面的重力加速度g和地球半径R,引力常量 G 。请计算地球的质量M ?
黄金代换
已知 g = 9.8m/s2,R =6.4×106m
引力常量G = 6.67×10-11 N·m2/kg2
试估算地球的质量
(保留一位有效数字)
6.0×1024 kg
一、“称量”地球的质量
1. 表面模型: 万有引力等于重力 mg = G ????????????????
?
(1). 求质量:
(2). 求密度:
已知球的体积公式V = ????????πR3 , 求地球的密度?
?
ρ = ????????????????????????
?
系统集成 第69页
[例2] 2019年1月3日,由我国发射的“嫦娥四号”首次实现人类探测器在月球背面的软着陆.地球表面的重力加速度是月球表面的重力加速度的6倍,地球半径为月球半径的4倍,则地球和月球的平均密度之比为( )
A.1.5
B.4
C.6
D.24
A
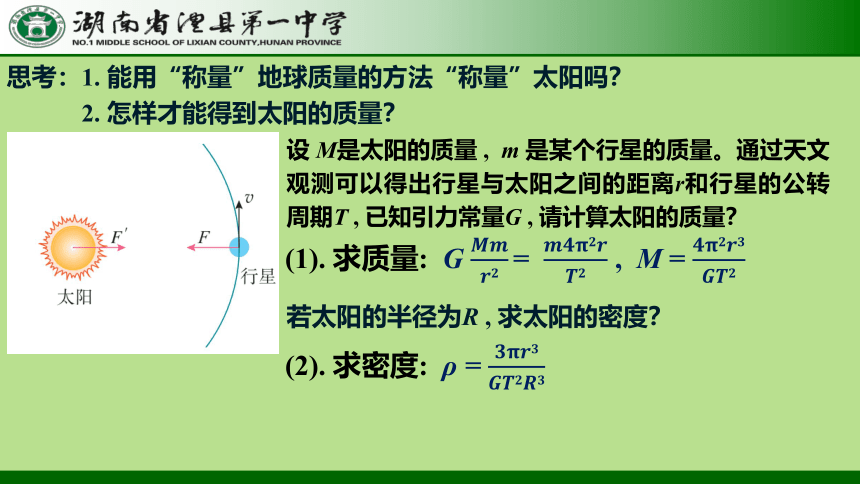
思考:1. 能用“称量”地球质量的方法“称量”太阳吗?
2. 怎样才能得到太阳的质量?
设 M是太阳的质量 , m 是某个行星的质量。通过天文观测可以得出行星与太阳之间的距离r和行星的公转周期T , 已知引力常量G , 请计算太阳的质量?
若太阳的半径为R , 求太阳的密度?
(1). 求质量: G ???????????????? = ???????????????????????????? , M = ????????????????????????????????
?
(2). 求密度: ρ = ????????????????????????????????????
?
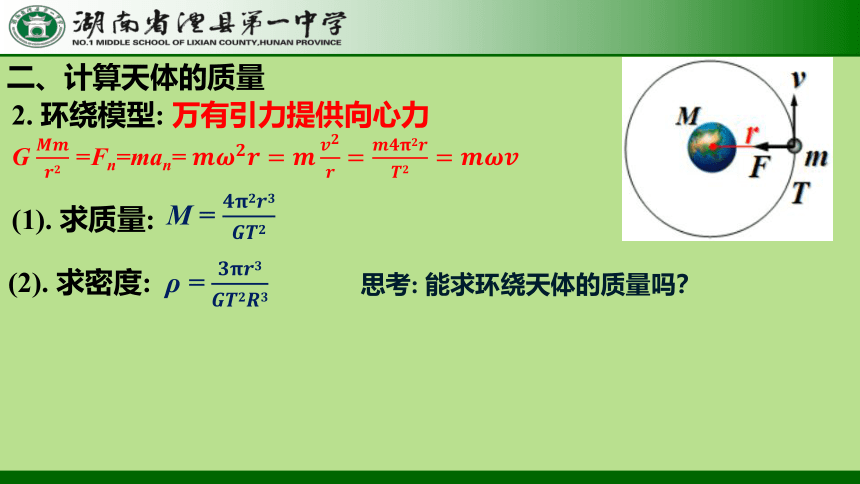
2. 环绕模型: 万有引力提供向心力
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
(1). 求质量:
二、计算天体的质量
M = ????????????????????????????????
?
(2). 求密度: ρ = ????????????????????????????????????
?
思考: 能求环绕天体的质量吗?
概念辨析:
(1)中心天体与环绕天体 :
用万有引力提供向心力只能求解中心天体质量 ,
不能求环绕天体(行星或卫星)的质量.
(2)球半径R、轨道半径r、高度h :
(3)公转周期和自转周期
中心天体M
环绕天体m
思考2. 三者的关系与区别?
概念辨析:
(1)中心天体与环绕天体 :
用万有引力提供向心力只能求解中心天体质量 ,
不能求环绕天体(行星或卫星)的质量.
(2)球半径R、轨道半径r、高度h :
1. R 指中心天体的半径
r 指环绕天体(行星或卫星)的轨道半径
h为环绕天体(行星或卫星)离中心天体表面的高度?
2. 关系:r=R+h
(3)公转周期和自转周期
中心天体M
环绕天体m
环绕天体m 在中心天体M 表面运行时:R = r
若环绕天体在中心天体表面运行时周期为T ,
求中心天体密度?(已知G, R, T)
[例1] 利用引力常量G和下列有关数据,不能计算出地球质量的是( )
A.地球的半径及重力加速度(不考虑地球自转)
B.人造卫星在地面附近绕地球做圆周运动的速度及周期
C.月球绕地球做圆周运动的周期及月球与地球间的距离
D.地球绕太阳做圆周运动的周期及地球与太阳间的距离
D
系统集成 第69页
(2015·江苏·高考真题)过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg??b”的发现拉开了研究太阳系外行星的序幕.“51 peg??b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径为????????????,该中心恒星与太阳的质量比约为(?? )
A.???????????? B.1 C.5 D.10
?
B
思考: 1. 能用开普勒第三定律吗?
2. 试推导开普勒第三定律中的k值?
[针对训练1] 已知地球半径为R,月球半径为r,地球与月球之间的距离(两球中心之间的距离)为L.月球绕地球公转的周期为T1,地球自转的周期为T2,地球绕太阳公转的周期为T3,假设公转运动都视为圆周运动,引力常量为G,由以上条件可知( )
A
系统集成 第70页
(2017·天津·高考真题)我国自主研制的首艘货运飞船“天舟一号”发射升空后,与已经在轨运行的“天宫二号”成功对接形成组合体.假设组合体在距地面高度为h的圆形轨道上绕地球做匀速圆周运动,已知地球的半径为R,地球表面处重力加速度为g,且不考虑地球自转的影响.则组合体运动的线速度大小为__________,向心加速度大小为___________。
黄金代换的应用
?? ????????????+??????????? ????????????(????+????)????
?
三、发现未知天体
(英)亚当斯 (法)勒维耶
1. 计算:英国剑桥大学学生亚当斯
法国年轻的天文学家勒维耶
2. 发现:1846 年 9 月 23 日晚,德国的伽勒
“笔尖下发现的行星”——海王星
四 、预言哈雷彗星回归
阅读教材:P57→P58
课堂小结
两
条
基
本
思
路
1. 表面模型: 万有引力等于重力
2. 环绕模型: 万有引力提供向心力
M = ????????????????????????????????
?
ρ = ????????????????????????????????????
?
mg = G ????????????????
?
M = ????????????????
?
黄金代换:GM = gR2
ρ = ????????????????????????
?
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
2.有两个行星A、B,在这两个行星表面附近各有一颗卫星,如果这两颗卫星运行的周期相等,则行星A、B的密度之比为( )
A.1∶1
B.2∶1
C.1∶2
D.无法计算
A
系统集成 第72页
(2007·全国·高考真题)据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面重量为600N的人在这个行星表面的重量将变为960N.由此可推知,该行星的半径与地球半径之比约为(???????)
A.0.5 B.2
C.3.2 D.4
B
据报道,天文学家日前在距离地球127光年处发现了一个拥有7颗行星的“太阳系”,这一星系的中央恒星名为“HD10180”.分析显示,其中一个行星N绕中央恒星“HD10180”的公转周期是地球绕太阳公转周期的3倍;与中央恒星“HD10180”的距离等于太阳和地球之间平均距离的5倍,将行星N与地球的公转轨道视为圆。图示为探测器在行星N上着陆最后阶段的模拟示意图。首先在发动机作用下,探测器受到推力作用在距行星N表面一定高度处(远小于行星N的半径)悬停;此后发动机突然关闭,探测器仅受重力下落2t时间(未着地),然后重新开启发动机使探测器匀减速下降,又经过时间t,探测器速度为0时恰好到达行星N表面。已知探测器总质量为m(不计燃料燃烧引起的质量变化),行星N和地球的半径之比为25,质量之比为16,地球表面附近的重力加速度为g,求:
(1)求恒星“HD10180”的质量与太阳的质量之比(2分)
(2)行星N的第一宇宙速度与地球的第一宇宙速度之比(3分)
(3)探测器匀减速下降时发动机对探测器的推力大小(5分)
????????????????
(计算质量和密度、黄金代换)
第七章 万有引力与宇宙航行
课前练.( 2014·海南·高考真题)设地球自转周期为T,质量为M,引力常量为G。假设地球可视为质量均匀分布的球体,半径为R 。同一物体在南极和赤道水平面上静止时所受到的支持力之比为( )
A.????????????????????????????????????????????????????? B.????????????????????????????????+????????????????????
C.????????????????????????????????????????????????????? D.????????????????+????????????????????????????????????
?
A
一、“称量”地球的质量
在初中,我们已经知道物体的质量可以用天平来测量。对于地球,我们怎样“称量”它的质量呢?
已知地面的重力加速度g和地球半径R,引力常量 G 。请计算地球的质量M ?
黄金代换
已知 g = 9.8m/s2,R =6.4×106m
引力常量G = 6.67×10-11 N·m2/kg2
试估算地球的质量
(保留一位有效数字)
6.0×1024 kg
一、“称量”地球的质量
1. 表面模型: 万有引力等于重力 mg = G ????????????????
?
(1). 求质量:
(2). 求密度:
已知球的体积公式V = ????????πR3 , 求地球的密度?
?
ρ = ????????????????????????
?
系统集成 第69页
[例2] 2019年1月3日,由我国发射的“嫦娥四号”首次实现人类探测器在月球背面的软着陆.地球表面的重力加速度是月球表面的重力加速度的6倍,地球半径为月球半径的4倍,则地球和月球的平均密度之比为( )
A.1.5
B.4
C.6
D.24
A
思考:1. 能用“称量”地球质量的方法“称量”太阳吗?
2. 怎样才能得到太阳的质量?
设 M是太阳的质量 , m 是某个行星的质量。通过天文观测可以得出行星与太阳之间的距离r和行星的公转周期T , 已知引力常量G , 请计算太阳的质量?
若太阳的半径为R , 求太阳的密度?
(1). 求质量: G ???????????????? = ???????????????????????????? , M = ????????????????????????????????
?
(2). 求密度: ρ = ????????????????????????????????????
?
2. 环绕模型: 万有引力提供向心力
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
(1). 求质量:
二、计算天体的质量
M = ????????????????????????????????
?
(2). 求密度: ρ = ????????????????????????????????????
?
思考: 能求环绕天体的质量吗?
概念辨析:
(1)中心天体与环绕天体 :
用万有引力提供向心力只能求解中心天体质量 ,
不能求环绕天体(行星或卫星)的质量.
(2)球半径R、轨道半径r、高度h :
(3)公转周期和自转周期
中心天体M
环绕天体m
思考2. 三者的关系与区别?
概念辨析:
(1)中心天体与环绕天体 :
用万有引力提供向心力只能求解中心天体质量 ,
不能求环绕天体(行星或卫星)的质量.
(2)球半径R、轨道半径r、高度h :
1. R 指中心天体的半径
r 指环绕天体(行星或卫星)的轨道半径
h为环绕天体(行星或卫星)离中心天体表面的高度?
2. 关系:r=R+h
(3)公转周期和自转周期
中心天体M
环绕天体m
环绕天体m 在中心天体M 表面运行时:R = r
若环绕天体在中心天体表面运行时周期为T ,
求中心天体密度?(已知G, R, T)
[例1] 利用引力常量G和下列有关数据,不能计算出地球质量的是( )
A.地球的半径及重力加速度(不考虑地球自转)
B.人造卫星在地面附近绕地球做圆周运动的速度及周期
C.月球绕地球做圆周运动的周期及月球与地球间的距离
D.地球绕太阳做圆周运动的周期及地球与太阳间的距离
D
系统集成 第69页
(2015·江苏·高考真题)过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg??b”的发现拉开了研究太阳系外行星的序幕.“51 peg??b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径为????????????,该中心恒星与太阳的质量比约为(?? )
A.???????????? B.1 C.5 D.10
?
B
思考: 1. 能用开普勒第三定律吗?
2. 试推导开普勒第三定律中的k值?
[针对训练1] 已知地球半径为R,月球半径为r,地球与月球之间的距离(两球中心之间的距离)为L.月球绕地球公转的周期为T1,地球自转的周期为T2,地球绕太阳公转的周期为T3,假设公转运动都视为圆周运动,引力常量为G,由以上条件可知( )
A
系统集成 第70页
(2017·天津·高考真题)我国自主研制的首艘货运飞船“天舟一号”发射升空后,与已经在轨运行的“天宫二号”成功对接形成组合体.假设组合体在距地面高度为h的圆形轨道上绕地球做匀速圆周运动,已知地球的半径为R,地球表面处重力加速度为g,且不考虑地球自转的影响.则组合体运动的线速度大小为__________,向心加速度大小为___________。
黄金代换的应用
?? ????????????+??????????? ????????????(????+????)????
?
三、发现未知天体
(英)亚当斯 (法)勒维耶
1. 计算:英国剑桥大学学生亚当斯
法国年轻的天文学家勒维耶
2. 发现:1846 年 9 月 23 日晚,德国的伽勒
“笔尖下发现的行星”——海王星
四 、预言哈雷彗星回归
阅读教材:P57→P58
课堂小结
两
条
基
本
思
路
1. 表面模型: 万有引力等于重力
2. 环绕模型: 万有引力提供向心力
M = ????????????????????????????????
?
ρ = ????????????????????????????????????
?
mg = G ????????????????
?
M = ????????????????
?
黄金代换:GM = gR2
ρ = ????????????????????????
?
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
2.有两个行星A、B,在这两个行星表面附近各有一颗卫星,如果这两颗卫星运行的周期相等,则行星A、B的密度之比为( )
A.1∶1
B.2∶1
C.1∶2
D.无法计算
A
系统集成 第72页
(2007·全国·高考真题)据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面重量为600N的人在这个行星表面的重量将变为960N.由此可推知,该行星的半径与地球半径之比约为(???????)
A.0.5 B.2
C.3.2 D.4
B
据报道,天文学家日前在距离地球127光年处发现了一个拥有7颗行星的“太阳系”,这一星系的中央恒星名为“HD10180”.分析显示,其中一个行星N绕中央恒星“HD10180”的公转周期是地球绕太阳公转周期的3倍;与中央恒星“HD10180”的距离等于太阳和地球之间平均距离的5倍,将行星N与地球的公转轨道视为圆。图示为探测器在行星N上着陆最后阶段的模拟示意图。首先在发动机作用下,探测器受到推力作用在距行星N表面一定高度处(远小于行星N的半径)悬停;此后发动机突然关闭,探测器仅受重力下落2t时间(未着地),然后重新开启发动机使探测器匀减速下降,又经过时间t,探测器速度为0时恰好到达行星N表面。已知探测器总质量为m(不计燃料燃烧引起的质量变化),行星N和地球的半径之比为25,质量之比为16,地球表面附近的重力加速度为g,求:
(1)求恒星“HD10180”的质量与太阳的质量之比(2分)
(2)行星N的第一宇宙速度与地球的第一宇宙速度之比(3分)
(3)探测器匀减速下降时发动机对探测器的推力大小(5分)
????????????????
