7.3.2 万有引力理论的成就 环绕天体的运行、双星系统 课件(共18张PPT)-物理人教版(2019)必修第二册
文档属性
| 名称 | 7.3.2 万有引力理论的成就 环绕天体的运行、双星系统 课件(共18张PPT)-物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-27 23:20:44 | ||
图片预览





文档简介
§7.32 万有引力理论的成就
(环绕天体的运行、双星系统)
第七章 万有引力与宇宙航行
课前练.(2020·全国·高考真题)若一均匀球形星体的密度为ρ,引力常量为G,则在该星体表面附近沿圆轨道绕其运动的卫星的周期是( )
A.???????????????? B.????????????????
C.???????????????????? D.????????????????????
?
A
知识回顾:默写!!!
两
条
基
本
思
路
1. 表面模型: 万有引力等于重力
2. 环绕模型: 万有引力提供向心力
M = ????????????????????????????????
?
ρ = ????????????????????????????????????
?
mg = G ????????????????
?
M = ??????????????
?
黄金代换:GM = gR2
ρ = ????????????????????????
?
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
已知地球、火星都绕太阳转动,火星的公转半径是地球的公转半径的1.5倍,
根据以上材料思考:
(1)地球、火星遵循什么样的动力学规律?
(2)如何比较火星与地球的线速度、角速度、周期以及向心加速度的大小?
系统集成 第70页
(1)环绕模型: 万有引力提供向心力
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
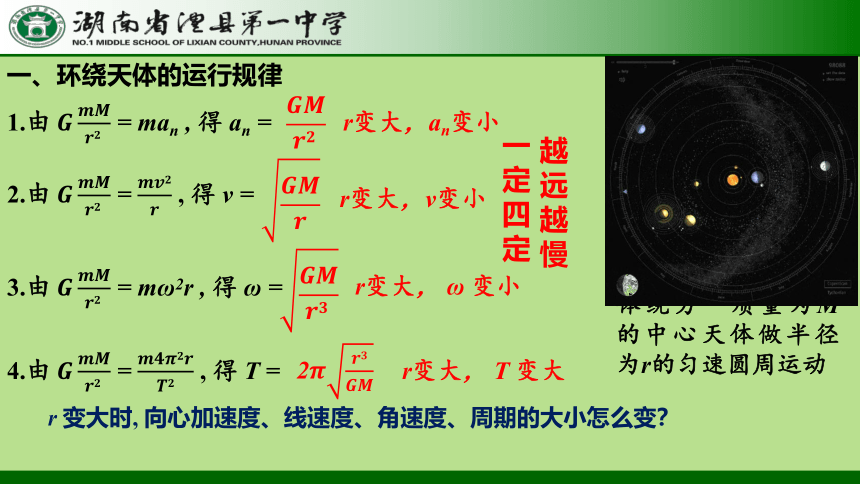
1.由?????????????????????? = man , 得 an =
?
设质量为m的环绕天体绕另一质量为M的中心天体做半径为r的匀速圆周运动
2.由?????????????????????? = ???????????????? , 得 v =
?
3.由?????????????????????? = mω2r , 得 ω =
?
4.由?????????????????????? = ???????????????????????????? , 得 T =
?
?????????????????
?
????????????
?
?????????????????
?
2????????????????????
?
r变大, ω 变小
r变大,v变小
r变大, T 变大
r变大,an变小
一、环绕天体的运行规律
r 变大时, 向心加速度、线速度、角速度、周期的大小怎么变?
越远越慢
一定四定
[针对训练2] (多选)如图所示,a、b、c是地球大气层外圈圆形轨道上运动的三颗卫星,a和b质量相等,且小于c的质量,则( )
A.b所需向心力最小
B.b、c的周期相同,且大于a的周期
C.b、c的向心加速度大小相等,且大于a的向心加速度
D.b、c的线速度大小相等,且小于a的线速度
ABD
系统集成 第71页
思考:若abc质量关系不清楚, 能不能比较abc所需向心力的大小?
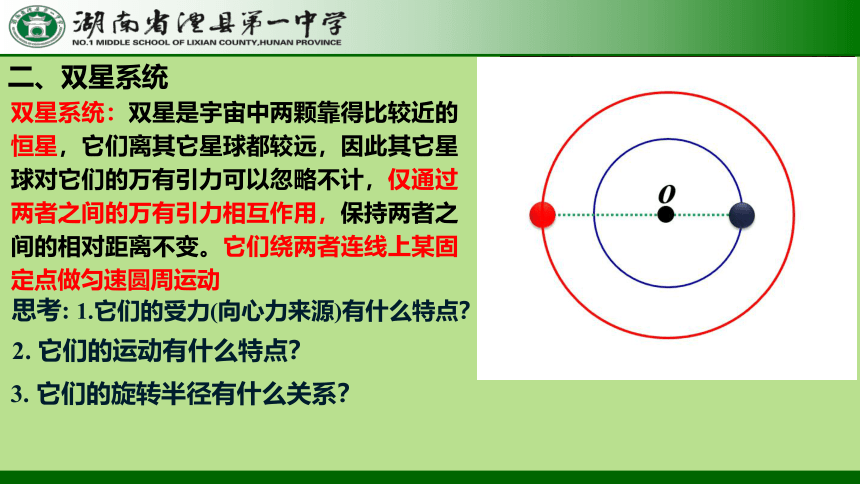
二、双星系统
双星系统:双星是宇宙中两颗靠得比较近的恒星,它们离其它星球都较远,因此其它星球对它们的万有引力可以忽略不计,仅通过两者之间的万有引力相互作用,保持两者之间的相对距离不变。它们绕两者连线上某固定点做匀速圆周运动
思考: 1.它们的受力(向心力来源)有什么特点?
2. 它们的运动有什么特点?
3. 它们的旋转半径有什么关系?
二、双星系统
(3). 双星的轨道半径之和等于双星之间的距离
即 r1+r2=L
(1). 向心力等大反向: Fn= ???????????????????????????? = m1ω2r1=m2ω2r2
?
(2). 周期T、角速度ω相同: ω1=ω2 , T1=T2
1.双星特点
二、双星系统
(3). r1+r2=L
(1). Fn= ????????????????????????????
?
(2). ω1=ω2 , T1=T2
1.双星特点
已知两双星质量m1、m2 , 距离为L , (引力常量为G)
求: (1).双星的轨道半径r1,r2之比
(2).双星的轨道半径r1,r2大小
(3).双星的角速度
2.双星规律
(3). ω =????(????????+?????????)?????????
?
(1). ????????????????? = ????????????????
?
(2). r1 = ?????????????????????+?????????? , r2 = ?????????????????????+??????????
?
质量 m 越大的星球, 旋转半径越小, 离旋转中心越近.
A.天狼星A和天狼星B的绕行方向可能相反
B.天狼星A和天狼星B的公共圆心可以不在质心连线上
C.天狼星A和天狼星B的向心加速度大小之比为b∶1
D.天狼星A和天狼星B的线速度大小之比为1∶b
[针对训练1] 人类通过哈勃太空望远镜曾拍摄到天狼星A和天狼星B组成的双星系统在轨运行图像,如图所示.它们在彼此间的万有引力作用下同时绕某点(公共圆心)做匀速圆周运动,已知mA=bmB,且b>1,则下列结论正确的是( )
系统集成 第71页
D
[针对训练2] 如图所示,两个星球A、B组成双星系统,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动.已知A、B星球的质量分别为mA、mB,引力常量为G.求????????????????(其中L为两星的中心距离,T为两星的运动周期).
?
系统集成 第72页
5.(多选)(2018·全国·高考真题)2017年,人类第一次直接探测到来自双中子星合并的引力波.根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈.将两颗中子星都看作是质量均匀分布的球体,由这些数据和引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )
A.质量之积 B.质量之和
C.速率之和 D.各自的自转角速度
系统集成 第73页
BC
课堂小结
一、环绕天体的运行规律:万有引力提供向心力
越远越慢
一定四定
二、双星系统
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
an =????????????????? , v =???????????? , ω =????????????????? , T =2????????????????????
?
(3). r1+r2=L
(2). ω1=ω2 , T1=T2
1.双星特点
2.双星规律
(1)运动半径与质量成反比: m1r1=m2r2
(1).万有引力提供向心力
????????????????????????????=m1ω2r1=m2ω2r2
?
(2)质量之和:m1+m2=????????????????????????????????
?
[例3] 火星直径约为地球的一半,质量约为地球的十分之一,它绕太阳公转的轨道半径约为地球公转半径的1.5倍.根据以上数据,以下说法正确的是( )
A.火星表面重力加速度的数值比地球表面的大
B.火星公转的周期比地球的长
C.火星公转的线速度比地球的大
D.火星公转的向心加速度比地球的大
系统集成 第70页
B
(2011·天津·高考真题)质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动.已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的( )
A.线速度????=???????????? B.角速度????=????????
C.运行周期????=???????????????? D.向心加速度????=????????????????
?
AC
(2022·河北·高考真题)2008年,我国天文学家利用国家天文台兴隆观测基地的2.16米望远镜,发现了一颗绕恒星HD173416运动的系外行星HD173416b,2019年,该恒星和行星被国际天文学联合会分别命名为“羲和”和“和“望舒”,天文观测得到恒星羲和的质量是太阳质量的2倍,若将望舒与地球的公转均视为匀速圆周运动,且公转的轨道半径相等。则望舒与地球公转速度大小的比值为(? ???)
A.???????? B.2 C.???? D.????????
?
C
(2010·重庆·高考真题)月球与地球质量之比约为1:80,有研究者认为月球和地球可视为一个由两质点构成的双星系统,他们都围绕月球连线上某点O做匀速圆周运动.据此观点,可知月球与地球绕O点运动的线速度大小之比约为 (?? ?)
A.1:6400 B.1:80
C.80:1 D.6400:1
C
(2020·浙江·高考真题)火星探测任务“天问一号”的标识如图所示。若火星和地球绕太阳的运动均可视为匀速圆周运动,火星公转轨道半径与地球公转轨道半径之比为3∶2,则火星与地球绕太阳运动的( )
A.轨道周长之比为2∶3
B.线速度大小之比为????:????
C.角速度大小之比为????????:????????
D.向心加速度大小之比为9∶4
?
C
(环绕天体的运行、双星系统)
第七章 万有引力与宇宙航行
课前练.(2020·全国·高考真题)若一均匀球形星体的密度为ρ,引力常量为G,则在该星体表面附近沿圆轨道绕其运动的卫星的周期是( )
A.???????????????? B.????????????????
C.???????????????????? D.????????????????????
?
A
知识回顾:默写!!!
两
条
基
本
思
路
1. 表面模型: 万有引力等于重力
2. 环绕模型: 万有引力提供向心力
M = ????????????????????????????????
?
ρ = ????????????????????????????????????
?
mg = G ????????????????
?
M = ??????????????
?
黄金代换:GM = gR2
ρ = ????????????????????????
?
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
已知地球、火星都绕太阳转动,火星的公转半径是地球的公转半径的1.5倍,
根据以上材料思考:
(1)地球、火星遵循什么样的动力学规律?
(2)如何比较火星与地球的线速度、角速度、周期以及向心加速度的大小?
系统集成 第70页
(1)环绕模型: 万有引力提供向心力
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
1.由?????????????????????? = man , 得 an =
?
设质量为m的环绕天体绕另一质量为M的中心天体做半径为r的匀速圆周运动
2.由?????????????????????? = ???????????????? , 得 v =
?
3.由?????????????????????? = mω2r , 得 ω =
?
4.由?????????????????????? = ???????????????????????????? , 得 T =
?
?????????????????
?
????????????
?
?????????????????
?
2????????????????????
?
r变大, ω 变小
r变大,v变小
r变大, T 变大
r变大,an变小
一、环绕天体的运行规律
r 变大时, 向心加速度、线速度、角速度、周期的大小怎么变?
越远越慢
一定四定
[针对训练2] (多选)如图所示,a、b、c是地球大气层外圈圆形轨道上运动的三颗卫星,a和b质量相等,且小于c的质量,则( )
A.b所需向心力最小
B.b、c的周期相同,且大于a的周期
C.b、c的向心加速度大小相等,且大于a的向心加速度
D.b、c的线速度大小相等,且小于a的线速度
ABD
系统集成 第71页
思考:若abc质量关系不清楚, 能不能比较abc所需向心力的大小?
二、双星系统
双星系统:双星是宇宙中两颗靠得比较近的恒星,它们离其它星球都较远,因此其它星球对它们的万有引力可以忽略不计,仅通过两者之间的万有引力相互作用,保持两者之间的相对距离不变。它们绕两者连线上某固定点做匀速圆周运动
思考: 1.它们的受力(向心力来源)有什么特点?
2. 它们的运动有什么特点?
3. 它们的旋转半径有什么关系?
二、双星系统
(3). 双星的轨道半径之和等于双星之间的距离
即 r1+r2=L
(1). 向心力等大反向: Fn= ???????????????????????????? = m1ω2r1=m2ω2r2
?
(2). 周期T、角速度ω相同: ω1=ω2 , T1=T2
1.双星特点
二、双星系统
(3). r1+r2=L
(1). Fn= ????????????????????????????
?
(2). ω1=ω2 , T1=T2
1.双星特点
已知两双星质量m1、m2 , 距离为L , (引力常量为G)
求: (1).双星的轨道半径r1,r2之比
(2).双星的轨道半径r1,r2大小
(3).双星的角速度
2.双星规律
(3). ω =????(????????+?????????)?????????
?
(1). ????????????????? = ????????????????
?
(2). r1 = ?????????????????????+?????????? , r2 = ?????????????????????+??????????
?
质量 m 越大的星球, 旋转半径越小, 离旋转中心越近.
A.天狼星A和天狼星B的绕行方向可能相反
B.天狼星A和天狼星B的公共圆心可以不在质心连线上
C.天狼星A和天狼星B的向心加速度大小之比为b∶1
D.天狼星A和天狼星B的线速度大小之比为1∶b
[针对训练1] 人类通过哈勃太空望远镜曾拍摄到天狼星A和天狼星B组成的双星系统在轨运行图像,如图所示.它们在彼此间的万有引力作用下同时绕某点(公共圆心)做匀速圆周运动,已知mA=bmB,且b>1,则下列结论正确的是( )
系统集成 第71页
D
[针对训练2] 如图所示,两个星球A、B组成双星系统,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动.已知A、B星球的质量分别为mA、mB,引力常量为G.求????????????????(其中L为两星的中心距离,T为两星的运动周期).
?
系统集成 第72页
5.(多选)(2018·全国·高考真题)2017年,人类第一次直接探测到来自双中子星合并的引力波.根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈.将两颗中子星都看作是质量均匀分布的球体,由这些数据和引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )
A.质量之积 B.质量之和
C.速率之和 D.各自的自转角速度
系统集成 第73页
BC
课堂小结
一、环绕天体的运行规律:万有引力提供向心力
越远越慢
一定四定
二、双星系统
G ???????????????? =Fn=man= ???????????????? =???????????????? =????????????????????????????=????????????
?
an =????????????????? , v =???????????? , ω =????????????????? , T =2????????????????????
?
(3). r1+r2=L
(2). ω1=ω2 , T1=T2
1.双星特点
2.双星规律
(1)运动半径与质量成反比: m1r1=m2r2
(1).万有引力提供向心力
????????????????????????????=m1ω2r1=m2ω2r2
?
(2)质量之和:m1+m2=????????????????????????????????
?
[例3] 火星直径约为地球的一半,质量约为地球的十分之一,它绕太阳公转的轨道半径约为地球公转半径的1.5倍.根据以上数据,以下说法正确的是( )
A.火星表面重力加速度的数值比地球表面的大
B.火星公转的周期比地球的长
C.火星公转的线速度比地球的大
D.火星公转的向心加速度比地球的大
系统集成 第70页
B
(2011·天津·高考真题)质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动.已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的( )
A.线速度????=???????????? B.角速度????=????????
C.运行周期????=???????????????? D.向心加速度????=????????????????
?
AC
(2022·河北·高考真题)2008年,我国天文学家利用国家天文台兴隆观测基地的2.16米望远镜,发现了一颗绕恒星HD173416运动的系外行星HD173416b,2019年,该恒星和行星被国际天文学联合会分别命名为“羲和”和“和“望舒”,天文观测得到恒星羲和的质量是太阳质量的2倍,若将望舒与地球的公转均视为匀速圆周运动,且公转的轨道半径相等。则望舒与地球公转速度大小的比值为(? ???)
A.???????? B.2 C.???? D.????????
?
C
(2010·重庆·高考真题)月球与地球质量之比约为1:80,有研究者认为月球和地球可视为一个由两质点构成的双星系统,他们都围绕月球连线上某点O做匀速圆周运动.据此观点,可知月球与地球绕O点运动的线速度大小之比约为 (?? ?)
A.1:6400 B.1:80
C.80:1 D.6400:1
C
(2020·浙江·高考真题)火星探测任务“天问一号”的标识如图所示。若火星和地球绕太阳的运动均可视为匀速圆周运动,火星公转轨道半径与地球公转轨道半径之比为3∶2,则火星与地球绕太阳运动的( )
A.轨道周长之比为2∶3
B.线速度大小之比为????:????
C.角速度大小之比为????????:????????
D.向心加速度大小之比为9∶4
?
C
