人教版七年级上册4.3.3余角和补角课件(共27张PPT)
文档属性
| 名称 | 人教版七年级上册4.3.3余角和补角课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
4.3.3 余角和补角
第四章 几何图形初步
4.3 角
一、余角、补角的概念:
∠A+∠C=90 °
问题1. 每块直角三角板中的两个锐角之间有什么相同的数量关系?
A
B
C
D
E
F
∠D+∠F=90 °
O
A
B
1
2
l
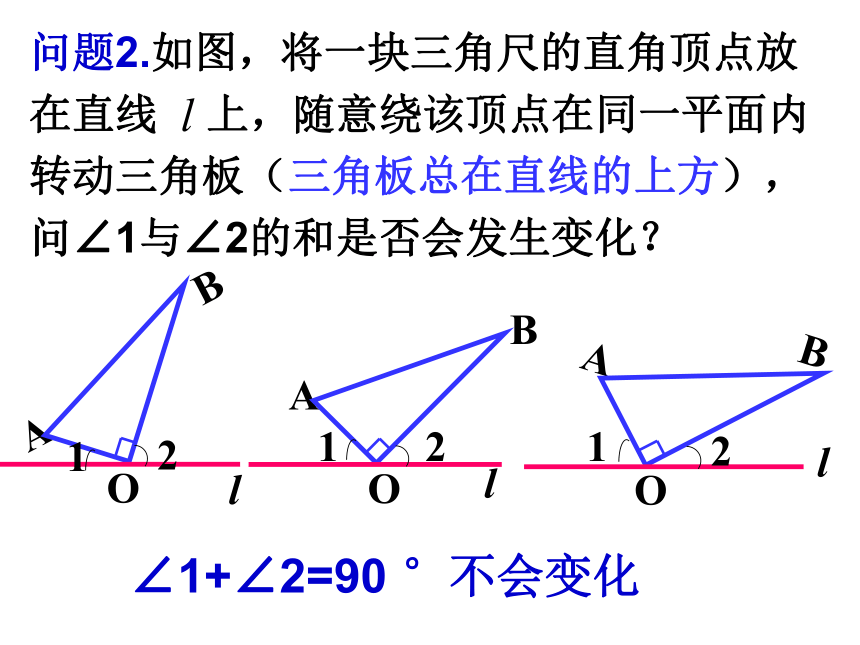
问题2.如图,将一块三角尺的直角顶点放在直线 上,随意绕该顶点在同一平面内转动三角板(三角板总在直线的上方),问∠1与∠2的和是否会发生变化?
O
A
B
1
2
l
O
A
B
1
2
l
∠1+∠2=90 °不会变化
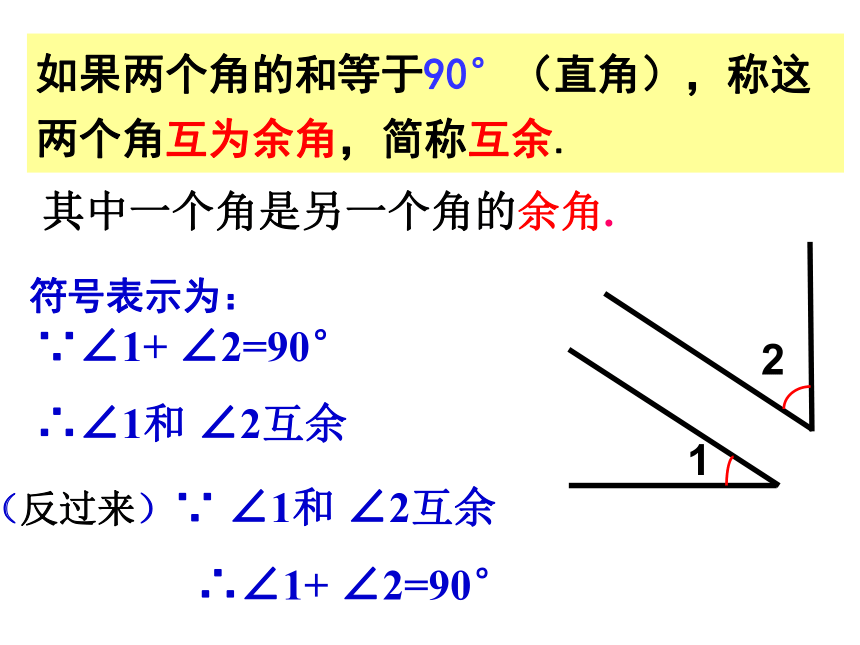
如果两个角的和等于90°(直角),称这两个角互为余角,简称互余.
其中一个角是另一个角的余角.
∵∠1+ ∠2=90°
∴∠1和 ∠2互余
(反过来)∵ ∠1和 ∠2互余
∴∠1+ ∠2=90°
符号表示为:
1
2
∠α+∠β的结果发生变化了吗?
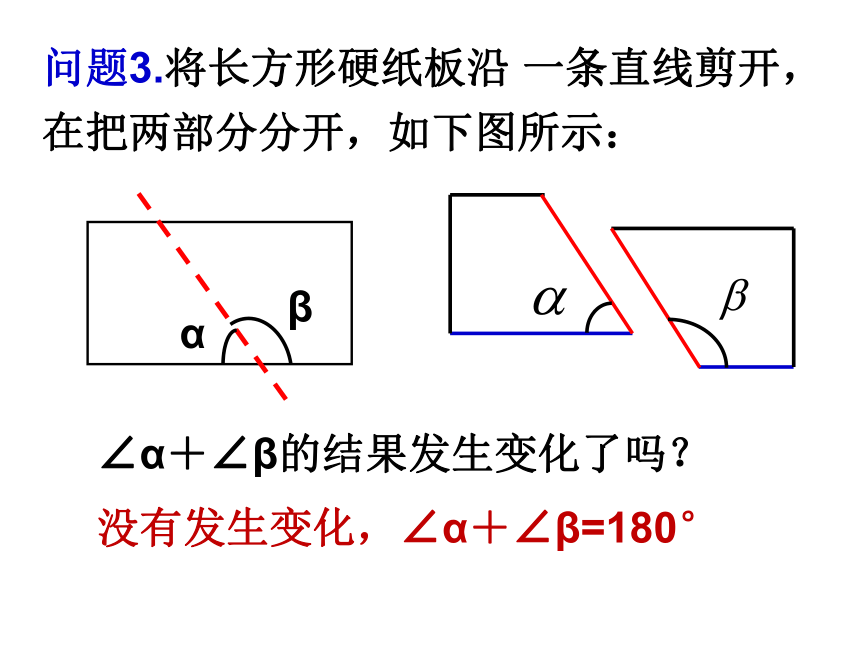
问题3.将长方形硬纸板沿 一条直线剪开,在把两部分分开,如下图所示:
α
β
没有发生变化,∠α+∠β=180°
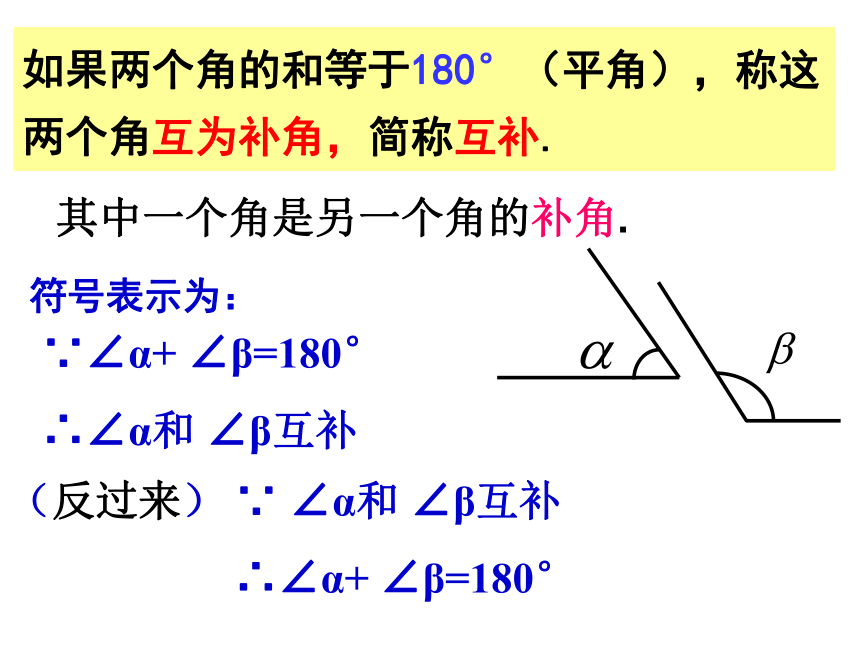
如果两个角的和等于180°(平角),称这两个角互为补角,简称互补.
(反过来) ∵ ∠α和 ∠β互补
∴∠α+ ∠β=180°
∵∠α+ ∠β=180°
∴∠α和 ∠β互补
其中一个角是另一个角的补角.
符号表示为:
练习1:
下列说法正确的是( )
A. ∠A是余角
B. 若∠1+∠2+∠3=180°,
则∠1,∠2,∠3 互补
C. 若∠1+∠2=180°,则∠1与∠2互余
D. 100°角的补角是80 °角
D
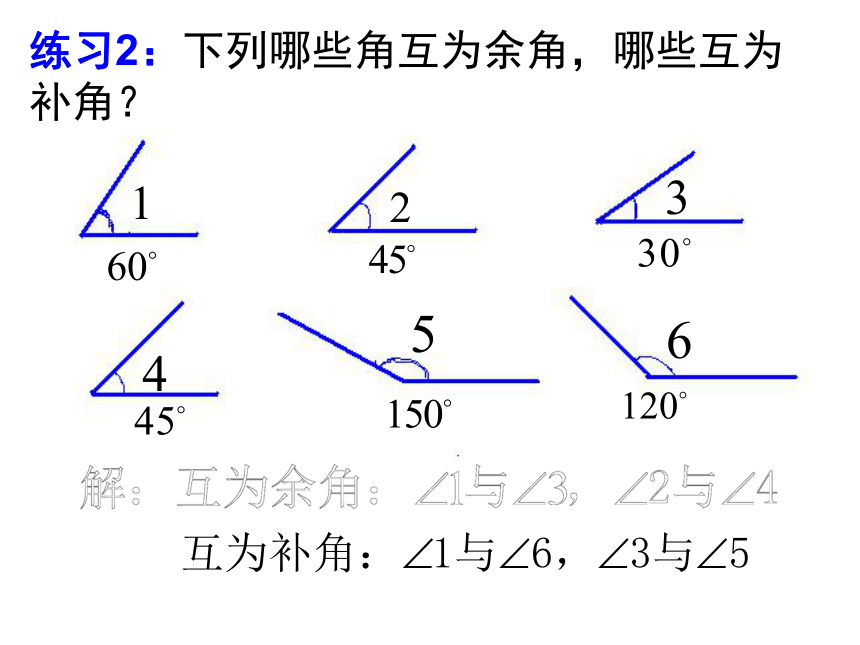
练习2:下列哪些角互为余角,哪些互为补角?
填空
同一个角的余角和补角之间有什么关系?
相差90度
练习3:
已知一个角的补角是这个角的余角的4倍,求这个角的度数?
解:设这个角为x°,则它的余是(90-x)° ,补角是(180-x)度。
180-x = 4(90-x)
解得:x = 60
答:这个角是60度.
练习4:
A
O
B
如图,要测量两堵围墙所形成的∠ AOB的度数,但人不能进入围墙,如何测量?
C
练习5:
2.图中∠α的余角∠1,∠2的大小有什么关系?为什么?
3.这一结论用文字怎么叙述?
同角的余角相等
α
1
2
(
1.画一画:已知∠α,请利用三角板画的∠α的余角
二、余角的性质:
1
3
2
4
等角的余角相等
3
思考:
性质1:同角(等角)的余角相等
α
1
2
1.画一画:已知∠α,请利用三角板画∠α的补角
2.图中∠α的补角∠1,∠2的大小有什么关系?为什么?
3.这一结论用文字怎么叙述?
三、补角的性质:
同角的补角相等
性质2:同角(等角)的补角相等
练习6:
例3 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC 和∠BOC,图中哪些角互为余角?
O
A
B
D
C
E
解:∵点A,O,B在同一条直线上
∴ ∠AOC +∠BOC=180°
又∵ OD、OE分别平分∠AOC 和∠BOC
∴ ∠COD +∠COE
= ∠AOC+ ∠BOC
= (∠AOC+ ∠BOC)
= 90°
西
北
南
O
B
C
D
45°
E
G
F
H
45°
45°
45°
四探究:方位角
直线AB和直线CD互相垂直,所成四个角均为直角
东
1)正北,正南,正西,正东,
2) 西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OD、
OC、
OB
射线OE
射线OF
射线OG
射线OH
A
2.南偏西25°
1.北偏东70°
70°
北
西
东
O
南
25°
A
B
探究:方位角
方位角是以正北、正南方向为基准,描述物体运动的方向(两条射线行成的角)
2.如图,OA表示北偏东32°方向线,OB表示南偏东43°方向线,则∠AOB等于 ———— 。
32°
43°
105°
A
B
O
北
东
3.如图,下列说法中错误的是( )
A.OA的方向是北偏西22 °
B. OC的方向是南偏东60°
C.OB的方向是西南方向。
D.OD的方向是北偏东60°
C
D
B
A
450
O
60°
30°
北
东
68°
D
例2.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示
灯塔方位的方法画出
表示客轮B,货轮C
和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
甲地
乙地
如何表示乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
北
观测点
被观测点
归纳
甲地
乙地
乙地对甲地的方位角
2.作一条射线以中心点为端点,目的地为射线上任一点。
北
视线
甲地
乙地
乙地对甲地的方位角
3.度量南北的射线和视线之间的角度
北
4.如图,A地和B地都是海上观测站,从A地发现它的北偏东500方向上有一艘船,同时从B地发现这艘船在它的北偏东300方向,试在图中确定这艘船的位置。
A
B
北
东
500
300
C
解:
则这艘船在点C处
●
A
南偏西40°
南
●
东
西
北
B
40°
400
C
D
1.说出B在A的____ ,那么A在B的______.
北偏东400
北
东
500
南
西
A是被观测点
B是观测点
拓展应用
互余 互补
对应 图形
两角间的数量 关系
性质
同角或等角的
余角相等
同角或等角的
补角相等
五、课堂小结:
4.3.3 余角和补角
第四章 几何图形初步
4.3 角
一、余角、补角的概念:
∠A+∠C=90 °
问题1. 每块直角三角板中的两个锐角之间有什么相同的数量关系?
A
B
C
D
E
F
∠D+∠F=90 °
O
A
B
1
2
l
问题2.如图,将一块三角尺的直角顶点放在直线 上,随意绕该顶点在同一平面内转动三角板(三角板总在直线的上方),问∠1与∠2的和是否会发生变化?
O
A
B
1
2
l
O
A
B
1
2
l
∠1+∠2=90 °不会变化
如果两个角的和等于90°(直角),称这两个角互为余角,简称互余.
其中一个角是另一个角的余角.
∵∠1+ ∠2=90°
∴∠1和 ∠2互余
(反过来)∵ ∠1和 ∠2互余
∴∠1+ ∠2=90°
符号表示为:
1
2
∠α+∠β的结果发生变化了吗?
问题3.将长方形硬纸板沿 一条直线剪开,在把两部分分开,如下图所示:
α
β
没有发生变化,∠α+∠β=180°
如果两个角的和等于180°(平角),称这两个角互为补角,简称互补.
(反过来) ∵ ∠α和 ∠β互补
∴∠α+ ∠β=180°
∵∠α+ ∠β=180°
∴∠α和 ∠β互补
其中一个角是另一个角的补角.
符号表示为:
练习1:
下列说法正确的是( )
A. ∠A是余角
B. 若∠1+∠2+∠3=180°,
则∠1,∠2,∠3 互补
C. 若∠1+∠2=180°,则∠1与∠2互余
D. 100°角的补角是80 °角
D
练习2:下列哪些角互为余角,哪些互为补角?
填空
同一个角的余角和补角之间有什么关系?
相差90度
练习3:
已知一个角的补角是这个角的余角的4倍,求这个角的度数?
解:设这个角为x°,则它的余是(90-x)° ,补角是(180-x)度。
180-x = 4(90-x)
解得:x = 60
答:这个角是60度.
练习4:
A
O
B
如图,要测量两堵围墙所形成的∠ AOB的度数,但人不能进入围墙,如何测量?
C
练习5:
2.图中∠α的余角∠1,∠2的大小有什么关系?为什么?
3.这一结论用文字怎么叙述?
同角的余角相等
α
1
2
(
1.画一画:已知∠α,请利用三角板画的∠α的余角
二、余角的性质:
1
3
2
4
等角的余角相等
3
思考:
性质1:同角(等角)的余角相等
α
1
2
1.画一画:已知∠α,请利用三角板画∠α的补角
2.图中∠α的补角∠1,∠2的大小有什么关系?为什么?
3.这一结论用文字怎么叙述?
三、补角的性质:
同角的补角相等
性质2:同角(等角)的补角相等
练习6:
例3 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC 和∠BOC,图中哪些角互为余角?
O
A
B
D
C
E
解:∵点A,O,B在同一条直线上
∴ ∠AOC +∠BOC=180°
又∵ OD、OE分别平分∠AOC 和∠BOC
∴ ∠COD +∠COE
= ∠AOC+ ∠BOC
= (∠AOC+ ∠BOC)
= 90°
西
北
南
O
B
C
D
45°
E
G
F
H
45°
45°
45°
四探究:方位角
直线AB和直线CD互相垂直,所成四个角均为直角
东
1)正北,正南,正西,正东,
2) 西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OD、
OC、
OB
射线OE
射线OF
射线OG
射线OH
A
2.南偏西25°
1.北偏东70°
70°
北
西
东
O
南
25°
A
B
探究:方位角
方位角是以正北、正南方向为基准,描述物体运动的方向(两条射线行成的角)
2.如图,OA表示北偏东32°方向线,OB表示南偏东43°方向线,则∠AOB等于 ———— 。
32°
43°
105°
A
B
O
北
东
3.如图,下列说法中错误的是( )
A.OA的方向是北偏西22 °
B. OC的方向是南偏东60°
C.OB的方向是西南方向。
D.OD的方向是北偏东60°
C
D
B
A
450
O
60°
30°
北
东
68°
D
例2.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示
灯塔方位的方法画出
表示客轮B,货轮C
和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
甲地
乙地
如何表示乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
北
观测点
被观测点
归纳
甲地
乙地
乙地对甲地的方位角
2.作一条射线以中心点为端点,目的地为射线上任一点。
北
视线
甲地
乙地
乙地对甲地的方位角
3.度量南北的射线和视线之间的角度
北
4.如图,A地和B地都是海上观测站,从A地发现它的北偏东500方向上有一艘船,同时从B地发现这艘船在它的北偏东300方向,试在图中确定这艘船的位置。
A
B
北
东
500
300
C
解:
则这艘船在点C处
●
A
南偏西40°
南
●
东
西
北
B
40°
400
C
D
1.说出B在A的____ ,那么A在B的______.
北偏东400
北
东
500
南
西
A是被观测点
B是观测点
拓展应用
互余 互补
对应 图形
两角间的数量 关系
性质
同角或等角的
余角相等
同角或等角的
补角相等
五、课堂小结:
