安徽省铜陵市第五中学2013-2014学年高二下学期第一次月考 数学试题
文档属性
| 名称 | 安徽省铜陵市第五中学2013-2014学年高二下学期第一次月考 数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 134.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-04 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
铜陵市第五中学2013-2014学年高二下学期数学月考试卷
满分150分 时间120分钟
1、选择题(每小题5分,共50分)
1.设原命题:若a+b≥2,则a,b 中至少有一个不小于1。则原命题与其逆命题
的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
2.过点(0,1)与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 仅有一个公共点的直线共有 ( )
A.1条 B. 2条 C.3条 D.4条
3.2x2-5x-3<0的一个必要不充分条件是( )
A.-<x<3 B.-<x<0 C.-3<x< D.-1<x<6
4.设F1,F2是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 =1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )21世纪教育网版权所有
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
5.函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=0 B.a+b=0 C.a=b D.a2+b2=0
6.不等式 对于恒成立,那么的取值范围是( )
A. B. C. D.
7.若直线y= HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 x与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 =1(a>0,b>0)的交点在实轴上的射影恰好为双曲线的焦点,则双曲线的离心率为( )21教育网
A.2 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 D.4
8. 已知点A(0,1)是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的一点,P点是椭圆上的动点,
则弦AP长度的最大值为 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.2 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D.4
9.无论m为任何实数,直线l:y=x+m与双曲线C: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 =1(b>0)恒有公共点,则双曲线C的离心率e的取值范围是( )21cnjy.com
A.(1,+∞) B.( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,+∞) C.( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,+∞) D.(2,+∞)
10、若点P为共焦点的椭圆 ( http: / / www.21cnjy.com )和双曲线 ( http: / / www.21cnjy.com )的一个交点, ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com )分别是它们的左右焦点.设椭圆离心率为 ( http: / / www.21cnjy.com ),双曲线离心率为 ( http: / / www.21cnjy.com ),若 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com ) ( )21·cn·jy·com
A. 4 B. 3 C. 2 D. 1
二、填空题(每小题5分,共25分)
11.命题“有理数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”的否定为 。
12. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的点, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 是椭圆的两个焦点, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的面积等于 .
13 设集合 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,那么点P(2,3) HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的充要条件是
14.过原点O作两条相互垂直的直线分别与椭圆P: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 交于A、C与B、D, 则四边形ABCD面积最小值为 . www.21-cn-jy.com
15.已知集合P={x|1≤x≤8,x∈Z},直线y=2x+1与双曲线mx2-ny2=1有且只有一
个公共点,其中m、n∈P,则满足上述条件的双曲线共有 个。
三、解答题(共75分,解答应写出必要的文字说明,证明过程或演算步骤)
16.(本小题12分)给定两个命题:对任意实数都有恒成立;:关于的方程有实数根;如果与中有且仅有一个为真命题,求实数的取值范围.2·1·c·n·j·y
17.(12分)已知点A(1,0)及圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。【来源:21·世纪·教育·网】
18、(12分)已知p: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,q: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的必要不充分条件,求实数m的取值范围。
19. (13分)双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的中心在原点,右焦点为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,渐近线方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
(Ⅰ)求双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的方程;
(Ⅱ)设直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 : HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 交于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 两点,问:当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 为何值时,以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 为直径的圆过原点;
20、(13分) 已知离心率为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的顶点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 恰好是双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的左右焦点,点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 上不同于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的任意一点,设直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的斜率分别为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .21·世纪*教育网
(1)求椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的标准方程;
(2)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,在焦点在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 轴上的椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 上求一点Q,使该点到直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的距离最大。
(3)试判断乘积“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ”的值是否与点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的位置有关,并证明你的结论;
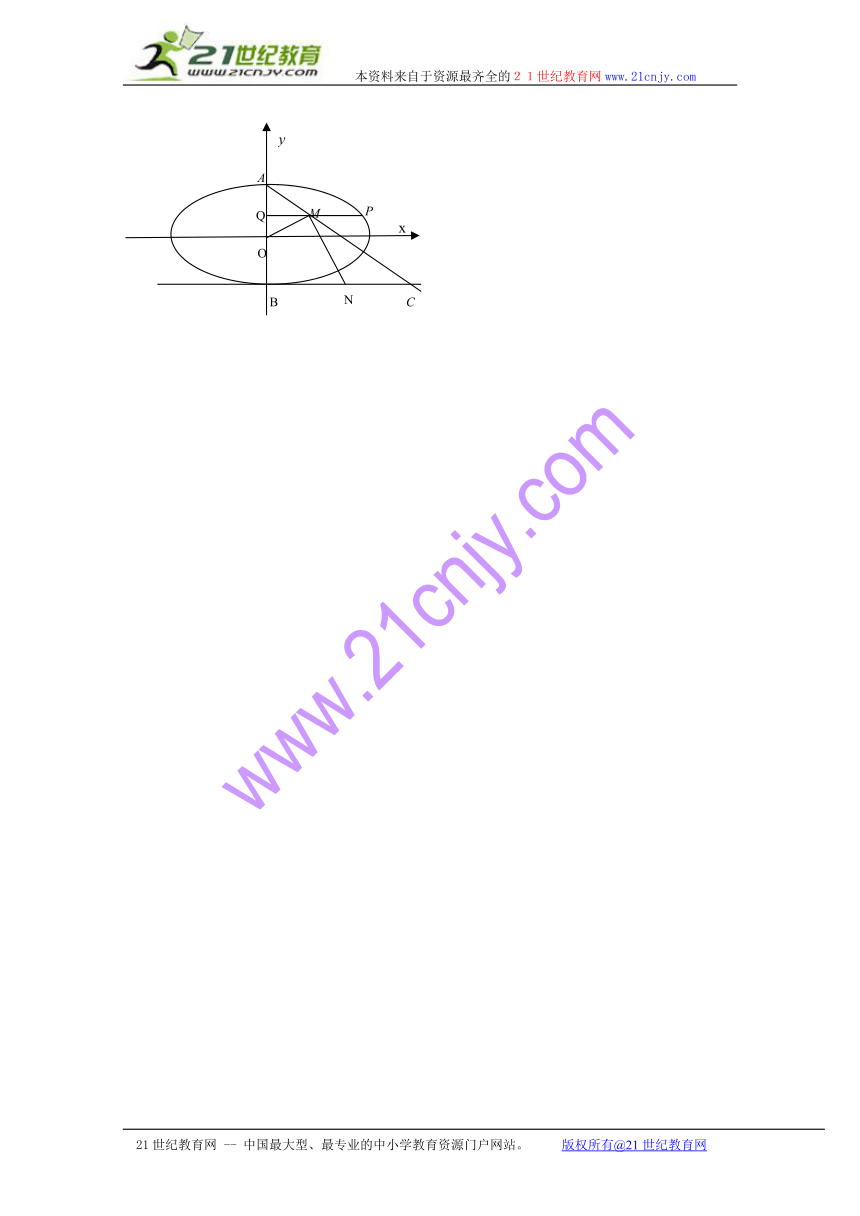
21. (本小题满分13分)如图,椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (a>b>0)的上、下顶点分别为A、B,已知点B在直线l: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上,且椭圆的离心率e = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .www-2-1-cnjy-com
(1)求椭圆的标准方程;
(2)设P是椭圆上异于A、B的任意一点, ( http: / / www.21cnjy.com )PQ⊥y轴,Q为垂足,M为线段PQ中点,直线AM交直线l于点C,N为线段BC的中点,求证:OM⊥MN.
班级: 姓 名: 考号: 密 封 线 内 不 要 答 题
高二数学答题卡
一、选择题(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(每小题5分,共25分)
11.
12. 13. 14. 15.
三、解答题(共75分,解答应写出必要的文字说明,证明过程或演算步骤)
16.
17.
18.
19.
20.
21.
参考答案
一.选择题
1 2 3 4 5 6 7 8 9 10
A D D C D B A C B C
二、填空题
11. 有理数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
12. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
13.m<-1,n<5
14. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
15.3
三、解答题
16.对任意实数都有恒成立
;关于的方程有实数根;如果P正确,且Q不正确,有;如果Q正确,且P不正确,有。所以实数的取值范围为。
17.连AP, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 垂直平分AC, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即点P的轨迹是以A、B为焦点的椭圆,
又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 点P的轨迹方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 。
18.解:由p: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
19. 解:(Ⅰ)易知 双曲线的方程是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
(Ⅱ)① 由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,因为以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 为直径的圆过原点,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
20解:(1)双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的左右焦点为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的坐标分别为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 所以设椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的标准方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,从而 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
所以椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的标准方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 或 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
(2) 当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,故直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
点Q( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
(3)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的值与点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的位置无关,恒为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
21解:(1)依题意,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . ∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴椭圆的标准方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
(2)证明:设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中点, ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的中点,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
此时 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 不存在,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
综上得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
A
Q
M
P
O
C
B
N
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
铜陵市第五中学2013-2014学年高二下学期数学月考试卷
满分150分 时间120分钟
1、选择题(每小题5分,共50分)
1.设原命题:若a+b≥2,则a,b 中至少有一个不小于1。则原命题与其逆命题
的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
2.过点(0,1)与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 仅有一个公共点的直线共有 ( )
A.1条 B. 2条 C.3条 D.4条
3.2x2-5x-3<0的一个必要不充分条件是( )
A.-<x<3 B.-<x<0 C.-3<x< D.-1<x<6
4.设F1,F2是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 =1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )21世纪教育网版权所有
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
5.函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=0 B.a+b=0 C.a=b D.a2+b2=0
6.不等式 对于恒成立,那么的取值范围是( )
A. B. C. D.
7.若直线y= HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 x与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 =1(a>0,b>0)的交点在实轴上的射影恰好为双曲线的焦点,则双曲线的离心率为( )21教育网
A.2 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 D.4
8. 已知点A(0,1)是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的一点,P点是椭圆上的动点,
则弦AP长度的最大值为 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.2 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D.4
9.无论m为任何实数,直线l:y=x+m与双曲线C: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 =1(b>0)恒有公共点,则双曲线C的离心率e的取值范围是( )21cnjy.com
A.(1,+∞) B.( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,+∞) C.( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,+∞) D.(2,+∞)
10、若点P为共焦点的椭圆 ( http: / / www.21cnjy.com )和双曲线 ( http: / / www.21cnjy.com )的一个交点, ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com )分别是它们的左右焦点.设椭圆离心率为 ( http: / / www.21cnjy.com ),双曲线离心率为 ( http: / / www.21cnjy.com ),若 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com ) ( )21·cn·jy·com
A. 4 B. 3 C. 2 D. 1
二、填空题(每小题5分,共25分)
11.命题“有理数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”的否定为 。
12. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的点, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 是椭圆的两个焦点, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的面积等于 .
13 设集合 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,那么点P(2,3) HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的充要条件是
14.过原点O作两条相互垂直的直线分别与椭圆P: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 交于A、C与B、D, 则四边形ABCD面积最小值为 . www.21-cn-jy.com
15.已知集合P={x|1≤x≤8,x∈Z},直线y=2x+1与双曲线mx2-ny2=1有且只有一
个公共点,其中m、n∈P,则满足上述条件的双曲线共有 个。
三、解答题(共75分,解答应写出必要的文字说明,证明过程或演算步骤)
16.(本小题12分)给定两个命题:对任意实数都有恒成立;:关于的方程有实数根;如果与中有且仅有一个为真命题,求实数的取值范围.2·1·c·n·j·y
17.(12分)已知点A(1,0)及圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。【来源:21·世纪·教育·网】
18、(12分)已知p: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,q: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的必要不充分条件,求实数m的取值范围。
19. (13分)双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的中心在原点,右焦点为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,渐近线方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
(Ⅰ)求双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的方程;
(Ⅱ)设直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 : HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 交于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 两点,问:当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 为何值时,以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 为直径的圆过原点;
20、(13分) 已知离心率为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的顶点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 恰好是双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的左右焦点,点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 是椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 上不同于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的任意一点,设直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的斜率分别为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .21·世纪*教育网
(1)求椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的标准方程;
(2)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,在焦点在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 轴上的椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 上求一点Q,使该点到直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的距离最大。
(3)试判断乘积“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ”的值是否与点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的位置有关,并证明你的结论;
21. (本小题满分13分)如图,椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (a>b>0)的上、下顶点分别为A、B,已知点B在直线l: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上,且椭圆的离心率e = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .www-2-1-cnjy-com
(1)求椭圆的标准方程;
(2)设P是椭圆上异于A、B的任意一点, ( http: / / www.21cnjy.com )PQ⊥y轴,Q为垂足,M为线段PQ中点,直线AM交直线l于点C,N为线段BC的中点,求证:OM⊥MN.
班级: 姓 名: 考号: 密 封 线 内 不 要 答 题
高二数学答题卡
一、选择题(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(每小题5分,共25分)
11.
12. 13. 14. 15.
三、解答题(共75分,解答应写出必要的文字说明,证明过程或演算步骤)
16.
17.
18.
19.
20.
21.
参考答案
一.选择题
1 2 3 4 5 6 7 8 9 10
A D D C D B A C B C
二、填空题
11. 有理数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
12. HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
13.m<-1,n<5
14. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
15.3
三、解答题
16.对任意实数都有恒成立
;关于的方程有实数根;如果P正确,且Q不正确,有;如果Q正确,且P不正确,有。所以实数的取值范围为。
17.连AP, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 垂直平分AC, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即点P的轨迹是以A、B为焦点的椭圆,
又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 点P的轨迹方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 。
18.解:由p: HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
19. 解:(Ⅰ)易知 双曲线的方程是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
(Ⅱ)① 由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,因为以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 为直径的圆过原点,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
20解:(1)双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的左右焦点为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的坐标分别为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 所以设椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的标准方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,从而 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
所以椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的标准方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 或 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
(2) 当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,故直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,
点Q( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
(3)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3
HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 . 所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的值与点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 的位置无关,恒为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
21解:(1)依题意,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . ∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴椭圆的标准方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
(2)证明:设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中点, ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的中点,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
此时 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 不存在,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
综上得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
A
Q
M
P
O
C
B
N
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
