江苏省南京市、盐城市2022-2023学年高三下学期2月开学摸底考试 数学 Word版含答案
文档属性
| 名称 | 江苏省南京市、盐城市2022-2023学年高三下学期2月开学摸底考试 数学 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 140.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 11:16:10 | ||
图片预览




文档简介
2022~2023学年高三年级模拟试卷
数 学
(满分:150分 考试时间:120分钟)
2023.2
一、 选择题:本题共8小题,每小题5分,共40分.在每小题给出的选项中只有一个选项符合要求.
1. “a3+a9=2a6”是“数列{an}为等差数列”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2. 若复数z满足|z-1|≤2,则复数z在复平面内对应点组成图形的面积为( )
A. π B. 2π C. 3π D. 4π
3. 已知集合A={x|<0},若A∩N*= ,则实数a的取值范围是( )
A. {1} B. (-∞,1)
C. [1,2] D. (-∞,2]
4. 把5个相同的小球分给3个小朋友,使每个小朋友都能分到小球的分法有( )
A. 4种 B. 6种 C. 21种 D. 35种
5. 某研究性学习小组发现,由双曲线C:-=1(a>0,b>0)的两渐近线所成的角可求离心率e的大小,联想到反比例函数y=(k≠0)的图象也是双曲线,据此可进一步推断双曲线y=的离心率为( )
A. B. 2 C. D. 5
6. 在△ABC中,AH为边BC上的高且=3,动点P满足·=-2,则点P的轨迹一定过△ABC的( )
A. 外心 B. 内心 C. 垂心 D. 重心
7. 若函数f(x)=x3+bx2+cx+d满足f(1-x)+f(1+x)=0对一切实数x恒成立,则不等式f′(2x+3)A. (0,+∞) B. (-∞,-4)
C. (-4,0) D. (-∞,-4)∪(0,+∞)
8. 已知四边形ABCD是矩形,AB=3AD,E,F分别是AB,CD的中点,将四边形AEFD绕EF旋转至与四边形BCFE重合,则直线ED,BF所成角α在旋转过程中( )
A. 逐步变大 B. 逐步变小
C. 先变小后变大 D. 先变大后变小
二、 选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 若X~N(μ,σ2),则下列说法正确的是( )
A. P(X<μ+σ)=P(X>μ-σ)
B. P(μ-2σC. P(X<μ+σ)不随μ,σ的变化而变化
D. P(μ-2σ10. 已知函数f(x) =3sin x-4cos x,若f(α),f(β)分别为f(x)的极大值与极小值,则( )
A. tan α=-tan β B. tan α=tan β
C. sin α=-sin β D. cos α=-cos β
11. 已知直线l的方程为(a2 -1)x-2ay+2a2+2=0,a∈R,O为原点,则( )
A. 若OP≤2,则点P一定不在直线l上
B. 若点P在直线l上,则OP≥2
C. 直线l上存在定点P
D. 存在无数个点P总不在直线l上
12. 如图,圆柱OO′的底面半径为1,高为2,矩形ABCD是其轴截面,过点A的平面α与圆柱底面所成的锐二面角为θ,平面α截圆柱侧面所得的曲线为椭圆Ω,截母线EF得点P,则( )
A. 椭圆Ω的短轴长为2
B. tan θ的最大值为2
C. 椭圆Ω的离心率的最大值为
D. EP=(1-cos ∠AOE)tan θ
三、 填空题:本题共4小题,每小题5分,共20分.
13. (2x+)5展开式中x3的系数为________.
14. 设函数f(x)=sin (ωx+)(ω>0),则使f(x)在(-,)上为增函数的ω的值可以为________(写出一个即可).
15. 在概率论中常用散度描述两个概率分布的差异.若离散型随机变量X,Y的取值集合均为{0,1,2,3,…,n}(n∈N*),则X,Y的散度D(X‖Y)=P(X=i)ln .若X,Y的概率分布如下表所示,其中0X 0 1
P
Y 0 1
P 1-p p
16. 已知数列{an},{bn}满足bn=其中k∈N*,{bn}是公比为q的等比数列,则=________(用q表示);若a2+b2=24,则a5=________.
四、 解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.
17. (本小题满分10分)
已知数列{an}满足a1=3,an+1=3an-4n,n∈N*.
(1) 试判断数列{an-2n-1}是否是等比数列,并求{an}的通项公式;
(2) 若bn=,求数列{bn}的前n项和Sn.
18. (本小题满分12分)
在△ABC中,已知AC=2,∠BAC=,P为△ABC内的一点,满足AP⊥CP,∠APB=.
(1) 若AP=PC,求△ABC的面积;
(2) 若BC=,求AP.
19. (本小题满分12分)
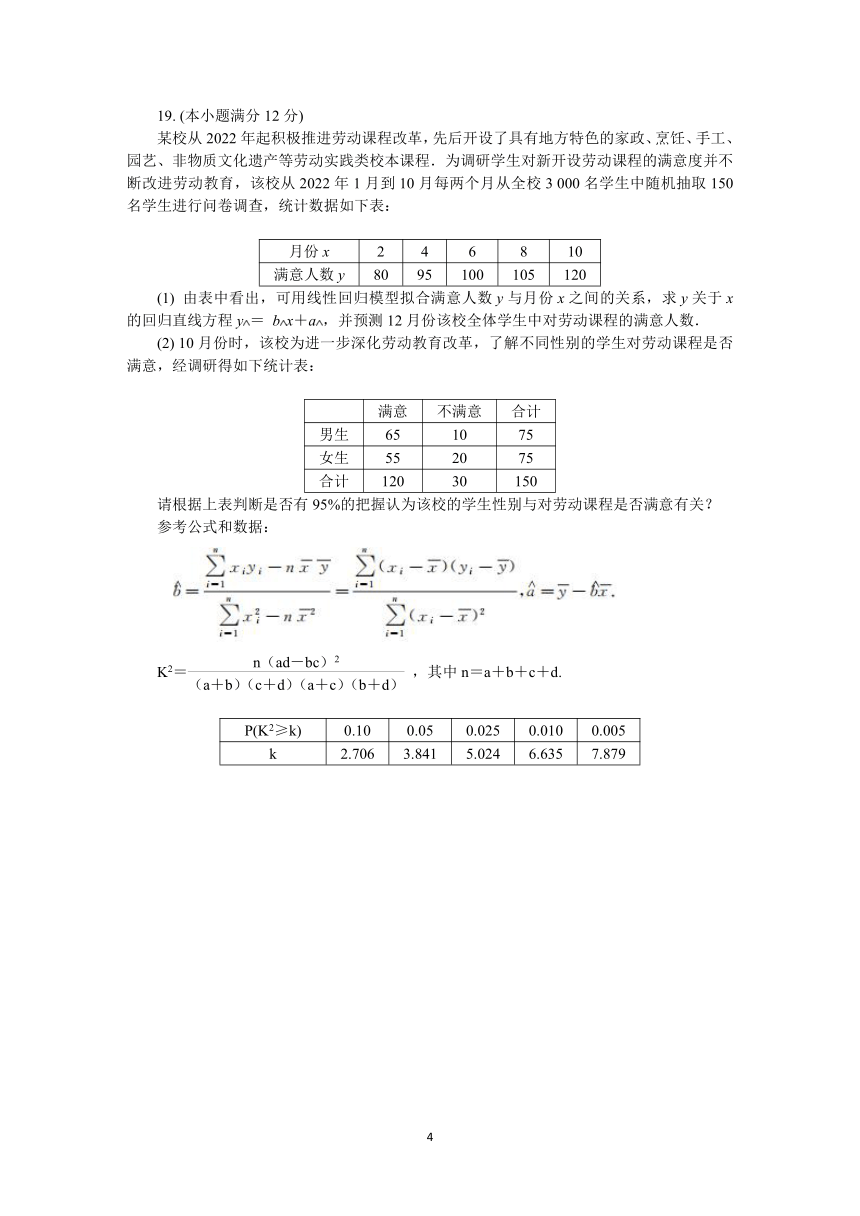
某校从2022年起积极推进劳动课程改革,先后开设了具有地方特色的家政、烹饪、手工、园艺、非物质文化遗产等劳动实践类校本课程.为调研学生对新开设劳动课程的满意度并不断改进劳动教育,该校从2022年1月到10月每两个月从全校3 000名学生中随机抽取150名学生进行问卷调查,统计数据如下表:
月份x 2 4 6 8 10
满意人数y 80 95 100 105 120
(1) 由表中看出,可用线性回归模型拟合满意人数y与月份x之间的关系,求y关于x的回归直线方程y= bx+a,并预测12月份该校全体学生中对劳动课程的满意人数.
(2) 10月份时,该校为进一步深化劳动教育改革,了解不同性别的学生对劳动课程是否满意,经调研得如下统计表:
满意 不满意 合计
男生 65 10 75
女生 55 20 75
合计 120 30 150
请根据上表判断是否有95%的把握认为该校的学生性别与对劳动课程是否满意有关?
参考公式和数据:
K2=,其中n=a+b+c+d.
P(K2≥k) 0.10 0.05 0.025 0.010 0.005
k 2.706 3.841 5.024 6.635 7.879
20. (本小题满分12分)
如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,平面PAC⊥平面PBD,AB=AD=AP=2,四棱锥PABCD的体积为4.
(1) 求证:BD⊥PC;
(2) 求平面PAD与平面PCD所成锐二面角的余弦值.
21. (本小题满分12分)
如图,已知椭圆+y2=1的左、右顶点分别为A,B,点C是椭圆上异于A,B的动点,过原点O平行于AC的直线与椭圆交于点M,N,AC的中点为点D,直线OD与椭圆交于点P,Q,点P,C,M在x轴的上方.
(1) 当AC=时,求cos ∠POM;
(2) 求PQ·MN的最大值.
22. (本小题满分12分)
已知函数f(x)=.
(1) 当x>-1时,求函数g(x)=f(x)+x2-1的最小值;
(2) 已知x1≠x2,f(x1)=f(x2)=t,求证:|x1-x2|>2.
2022~2023学年高三年级模拟试卷(南京、盐城)
数学参考答案及评分标准
1. B 2. D 3. D 4. B 5. A 6. A 7. C 8. D 9. AC 10. BCD 11. BD 12. ACD
13. 80 14. (答案不唯一,满足0<ω≤即可) 15. [0,+∞) 16. q2 1 024
17. 解:(1) 因为a1=3,所以a1-2×1-1=0,所以数列{an-2n-1}不是等比数列.(2分)
由an+1=3an-4n,得an+1-2(n+1)-1=3(an-2n-1),因为a1-2×1-1=0,
所以an-2n-1=0,即an=2n+1.(5分)
(2) 因为bn==-,(7分)
所以Sn=(-)+(-)+…+(-)=-.(10分)
18. 解:(1) 因为AP⊥CP,且AP=CP,所以∠CAP=,
又∠BAC=,所以∠BAP=,因为∠APB=,所以∠ABP=.
由AC=2,所以AP=,在△ABP中,由正弦定理,得=,
解得AB=,所以S△ABC=×AC×AB sin ∠BAC=××2×=. (5分)
(2) 在△ABC中,由余弦定理,得7=4+AB2-2AB,所以AB=3.(7分)
令∠CAP=α,则∠BAP=-α,∠ABP=α,在△APC中,AP=2cos α.(9分)
在△ABP中,由正弦定理,得=,所以tan α=,(11分)
因为α∈(0,),所以α=,所以AP=2×=.(12分)
19. 解:(1) x=(2+4+6+8+10)=6,y=(80+95+100+105+120)=100,
(xi-x)(yi-y)=(2-6)(80-100)+(4-6)(95-100)+(6-6)(100-100)+(8-6)(105-100)+(10-6)(120-100)=80+10+0+10+80=180,
==,(2分)
a=100-×6=73,(3分)
得y关于x的回归直线方程为y=x+73,(4分)
令x=12,得y=127,(5分)
据此预测12月份该校全体学生中对劳动课程的满意人数为3 000×=2 540(人).(6分)
(2) 提出假设H0:该校的学生性别与对劳动课程是否满意无关.(8分)
则K2===≈4.17,(10分)
因为P(K2≥3.841)=0.05,而4.17>3.841,
故有95%的把握认为该校的学生性别与对劳动课程是否满意有关.(12分)
20. (1) 证明:设AC∩BD=O,在平面PAC内过点A作AH⊥PO,垂足为H,
因为平面PAC⊥平面PBD,平面PAC∩平面PBD=PO,
所以AH⊥平面PBD.(3分)
又BD 平面PBD,所以BD⊥AH.
因为PA⊥平面ABCD,BD 平面ABCD,所以BD⊥PA.
因为BD⊥AH,PA∩AH=A,PA 平面PAC,AH 平面PAC,
所以BD⊥平面PAC,又因为PC 平面PAC,所以BD⊥PC.(6分)
(2) 解:由AB=AD=2,AB⊥AD知BD=2,
由(1)知BD⊥AC,所以VPABCD=S四边形ABCD×PA=××2×AC×2=4,
所以AC=3.(8分)
以{,,}为基底建立如图所示空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),D(0,2,0),C(3,3,0),P(0,0,2),易知平面PAD的一个法向量为n1=(1,0,0),
设平面PCD的法向量为n2=(x,y,z),又=(0,2,-2),=(3,3,-2),
得取z=3,则x=-1,y=3,则n2=(-1,3,3),(10分)
所以cos 〈n1,n2〉==-,(11分)
所以平面PAD与平面PCD所成锐二面角的余弦值为.(12分)
21. 解:(1)由AC=知点C(0,1),
因为D为AC的中点,且A(-2,0),所以D(-1,),所以kAC=,kOP=-,(2分)
(解法1)直线MN的方程为y=x,
联立方程得yM=,所以M(,),同理P(-,),
所以cos ∠POM==-.(4分)
(解法2)由kOM= ,kOP=-知∠POM=π-2∠MOB,由kOM=知tan ∠BOM=,
所以cos ∠BOM=,所以cos ∠POM=cos (π-2∠MOB)=-.(4分)
(解法3)由∠POM=〈,〉=〈,〉=〈,〉求解.
(2) 设点C(x0,y0),由A(-2,0)知D(,),
则kAC=kOM=,kOP=kOD=,kOM·kOP=·===-,(6分)
设直线OM的方程为y=kx,
联立方程得x2=,y2=,则OM2=,(8分)
由kOM·kOP=-,知OP2=,
(解法1)OM2·OP2=·,(10分)
令1+4k2=t,t>1,则OM2·OP2==-9()2++4≤(当t=2时取等号),
所以PQ·MN的最大值为10.(12分)
(解法2)由OM2+OP2=+=5,知OM·OP≤=,
当且仅当OM=OP=时取等号,所以PQ·MN的最大值为10.(12分)
22. (1) 解:当x>-1时,g′(x)=(ex-),(1分)
令g′(x)=0,可得x1=-ln 2>-1,x2=0,列表分析如下:
x (-1,-ln 2) -ln 2 (-ln 2,0) 0 (0,+∞)
g′(x) + 0 - 0 +
g(x) 增 极大值 减 极小值 增
可知g(x)min=g(-1)=g(0)=0,故函数的最小值为0.(5分)
(2) 证明:由(1)可知,当x>-1时,g(x)≥0,即≥1-x2(当且仅当x=0时取等号),
不妨取h(x)=1-x2,则在区间(-1,0)和(0,+∞)上,都有f(x)>h(x),
且h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,又由f′(x)=可知f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,且f(x)>0在(-1,0)和(0,+∞)上恒成立.(8分)
由x1≠x2,f(x1)=f(x2)=t,得0设h(x3)=h(x4)=t且x3<0同理0|x3-x4|,其中x3,x4为方程h(x)=t的两个实根,
而x3,4=±,所以|x1-x2|>2成立.(12分)
(
10
)
数 学
(满分:150分 考试时间:120分钟)
2023.2
一、 选择题:本题共8小题,每小题5分,共40分.在每小题给出的选项中只有一个选项符合要求.
1. “a3+a9=2a6”是“数列{an}为等差数列”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2. 若复数z满足|z-1|≤2,则复数z在复平面内对应点组成图形的面积为( )
A. π B. 2π C. 3π D. 4π
3. 已知集合A={x|<0},若A∩N*= ,则实数a的取值范围是( )
A. {1} B. (-∞,1)
C. [1,2] D. (-∞,2]
4. 把5个相同的小球分给3个小朋友,使每个小朋友都能分到小球的分法有( )
A. 4种 B. 6种 C. 21种 D. 35种
5. 某研究性学习小组发现,由双曲线C:-=1(a>0,b>0)的两渐近线所成的角可求离心率e的大小,联想到反比例函数y=(k≠0)的图象也是双曲线,据此可进一步推断双曲线y=的离心率为( )
A. B. 2 C. D. 5
6. 在△ABC中,AH为边BC上的高且=3,动点P满足·=-2,则点P的轨迹一定过△ABC的( )
A. 外心 B. 内心 C. 垂心 D. 重心
7. 若函数f(x)=x3+bx2+cx+d满足f(1-x)+f(1+x)=0对一切实数x恒成立,则不等式f′(2x+3)
C. (-4,0) D. (-∞,-4)∪(0,+∞)
8. 已知四边形ABCD是矩形,AB=3AD,E,F分别是AB,CD的中点,将四边形AEFD绕EF旋转至与四边形BCFE重合,则直线ED,BF所成角α在旋转过程中( )
A. 逐步变大 B. 逐步变小
C. 先变小后变大 D. 先变大后变小
二、 选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 若X~N(μ,σ2),则下列说法正确的是( )
A. P(X<μ+σ)=P(X>μ-σ)
B. P(μ-2σ
D. P(μ-2σ
A. tan α=-tan β B. tan α=tan β
C. sin α=-sin β D. cos α=-cos β
11. 已知直线l的方程为(a2 -1)x-2ay+2a2+2=0,a∈R,O为原点,则( )
A. 若OP≤2,则点P一定不在直线l上
B. 若点P在直线l上,则OP≥2
C. 直线l上存在定点P
D. 存在无数个点P总不在直线l上
12. 如图,圆柱OO′的底面半径为1,高为2,矩形ABCD是其轴截面,过点A的平面α与圆柱底面所成的锐二面角为θ,平面α截圆柱侧面所得的曲线为椭圆Ω,截母线EF得点P,则( )
A. 椭圆Ω的短轴长为2
B. tan θ的最大值为2
C. 椭圆Ω的离心率的最大值为
D. EP=(1-cos ∠AOE)tan θ
三、 填空题:本题共4小题,每小题5分,共20分.
13. (2x+)5展开式中x3的系数为________.
14. 设函数f(x)=sin (ωx+)(ω>0),则使f(x)在(-,)上为增函数的ω的值可以为________(写出一个即可).
15. 在概率论中常用散度描述两个概率分布的差异.若离散型随机变量X,Y的取值集合均为{0,1,2,3,…,n}(n∈N*),则X,Y的散度D(X‖Y)=P(X=i)ln .若X,Y的概率分布如下表所示,其中0
P
Y 0 1
P 1-p p
16. 已知数列{an},{bn}满足bn=其中k∈N*,{bn}是公比为q的等比数列,则=________(用q表示);若a2+b2=24,则a5=________.
四、 解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.
17. (本小题满分10分)
已知数列{an}满足a1=3,an+1=3an-4n,n∈N*.
(1) 试判断数列{an-2n-1}是否是等比数列,并求{an}的通项公式;
(2) 若bn=,求数列{bn}的前n项和Sn.
18. (本小题满分12分)
在△ABC中,已知AC=2,∠BAC=,P为△ABC内的一点,满足AP⊥CP,∠APB=.
(1) 若AP=PC,求△ABC的面积;
(2) 若BC=,求AP.
19. (本小题满分12分)
某校从2022年起积极推进劳动课程改革,先后开设了具有地方特色的家政、烹饪、手工、园艺、非物质文化遗产等劳动实践类校本课程.为调研学生对新开设劳动课程的满意度并不断改进劳动教育,该校从2022年1月到10月每两个月从全校3 000名学生中随机抽取150名学生进行问卷调查,统计数据如下表:
月份x 2 4 6 8 10
满意人数y 80 95 100 105 120
(1) 由表中看出,可用线性回归模型拟合满意人数y与月份x之间的关系,求y关于x的回归直线方程y= bx+a,并预测12月份该校全体学生中对劳动课程的满意人数.
(2) 10月份时,该校为进一步深化劳动教育改革,了解不同性别的学生对劳动课程是否满意,经调研得如下统计表:
满意 不满意 合计
男生 65 10 75
女生 55 20 75
合计 120 30 150
请根据上表判断是否有95%的把握认为该校的学生性别与对劳动课程是否满意有关?
参考公式和数据:
K2=,其中n=a+b+c+d.
P(K2≥k) 0.10 0.05 0.025 0.010 0.005
k 2.706 3.841 5.024 6.635 7.879
20. (本小题满分12分)
如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,平面PAC⊥平面PBD,AB=AD=AP=2,四棱锥PABCD的体积为4.
(1) 求证:BD⊥PC;
(2) 求平面PAD与平面PCD所成锐二面角的余弦值.
21. (本小题满分12分)
如图,已知椭圆+y2=1的左、右顶点分别为A,B,点C是椭圆上异于A,B的动点,过原点O平行于AC的直线与椭圆交于点M,N,AC的中点为点D,直线OD与椭圆交于点P,Q,点P,C,M在x轴的上方.
(1) 当AC=时,求cos ∠POM;
(2) 求PQ·MN的最大值.
22. (本小题满分12分)
已知函数f(x)=.
(1) 当x>-1时,求函数g(x)=f(x)+x2-1的最小值;
(2) 已知x1≠x2,f(x1)=f(x2)=t,求证:|x1-x2|>2.
2022~2023学年高三年级模拟试卷(南京、盐城)
数学参考答案及评分标准
1. B 2. D 3. D 4. B 5. A 6. A 7. C 8. D 9. AC 10. BCD 11. BD 12. ACD
13. 80 14. (答案不唯一,满足0<ω≤即可) 15. [0,+∞) 16. q2 1 024
17. 解:(1) 因为a1=3,所以a1-2×1-1=0,所以数列{an-2n-1}不是等比数列.(2分)
由an+1=3an-4n,得an+1-2(n+1)-1=3(an-2n-1),因为a1-2×1-1=0,
所以an-2n-1=0,即an=2n+1.(5分)
(2) 因为bn==-,(7分)
所以Sn=(-)+(-)+…+(-)=-.(10分)
18. 解:(1) 因为AP⊥CP,且AP=CP,所以∠CAP=,
又∠BAC=,所以∠BAP=,因为∠APB=,所以∠ABP=.
由AC=2,所以AP=,在△ABP中,由正弦定理,得=,
解得AB=,所以S△ABC=×AC×AB sin ∠BAC=××2×=. (5分)
(2) 在△ABC中,由余弦定理,得7=4+AB2-2AB,所以AB=3.(7分)
令∠CAP=α,则∠BAP=-α,∠ABP=α,在△APC中,AP=2cos α.(9分)
在△ABP中,由正弦定理,得=,所以tan α=,(11分)
因为α∈(0,),所以α=,所以AP=2×=.(12分)
19. 解:(1) x=(2+4+6+8+10)=6,y=(80+95+100+105+120)=100,
(xi-x)(yi-y)=(2-6)(80-100)+(4-6)(95-100)+(6-6)(100-100)+(8-6)(105-100)+(10-6)(120-100)=80+10+0+10+80=180,
==,(2分)
a=100-×6=73,(3分)
得y关于x的回归直线方程为y=x+73,(4分)
令x=12,得y=127,(5分)
据此预测12月份该校全体学生中对劳动课程的满意人数为3 000×=2 540(人).(6分)
(2) 提出假设H0:该校的学生性别与对劳动课程是否满意无关.(8分)
则K2===≈4.17,(10分)
因为P(K2≥3.841)=0.05,而4.17>3.841,
故有95%的把握认为该校的学生性别与对劳动课程是否满意有关.(12分)
20. (1) 证明:设AC∩BD=O,在平面PAC内过点A作AH⊥PO,垂足为H,
因为平面PAC⊥平面PBD,平面PAC∩平面PBD=PO,
所以AH⊥平面PBD.(3分)
又BD 平面PBD,所以BD⊥AH.
因为PA⊥平面ABCD,BD 平面ABCD,所以BD⊥PA.
因为BD⊥AH,PA∩AH=A,PA 平面PAC,AH 平面PAC,
所以BD⊥平面PAC,又因为PC 平面PAC,所以BD⊥PC.(6分)
(2) 解:由AB=AD=2,AB⊥AD知BD=2,
由(1)知BD⊥AC,所以VPABCD=S四边形ABCD×PA=××2×AC×2=4,
所以AC=3.(8分)
以{,,}为基底建立如图所示空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),D(0,2,0),C(3,3,0),P(0,0,2),易知平面PAD的一个法向量为n1=(1,0,0),
设平面PCD的法向量为n2=(x,y,z),又=(0,2,-2),=(3,3,-2),
得取z=3,则x=-1,y=3,则n2=(-1,3,3),(10分)
所以cos 〈n1,n2〉==-,(11分)
所以平面PAD与平面PCD所成锐二面角的余弦值为.(12分)
21. 解:(1)由AC=知点C(0,1),
因为D为AC的中点,且A(-2,0),所以D(-1,),所以kAC=,kOP=-,(2分)
(解法1)直线MN的方程为y=x,
联立方程得yM=,所以M(,),同理P(-,),
所以cos ∠POM==-.(4分)
(解法2)由kOM= ,kOP=-知∠POM=π-2∠MOB,由kOM=知tan ∠BOM=,
所以cos ∠BOM=,所以cos ∠POM=cos (π-2∠MOB)=-.(4分)
(解法3)由∠POM=〈,〉=〈,〉=〈,〉求解.
(2) 设点C(x0,y0),由A(-2,0)知D(,),
则kAC=kOM=,kOP=kOD=,kOM·kOP=·===-,(6分)
设直线OM的方程为y=kx,
联立方程得x2=,y2=,则OM2=,(8分)
由kOM·kOP=-,知OP2=,
(解法1)OM2·OP2=·,(10分)
令1+4k2=t,t>1,则OM2·OP2==-9()2++4≤(当t=2时取等号),
所以PQ·MN的最大值为10.(12分)
(解法2)由OM2+OP2=+=5,知OM·OP≤=,
当且仅当OM=OP=时取等号,所以PQ·MN的最大值为10.(12分)
22. (1) 解:当x>-1时,g′(x)=(ex-),(1分)
令g′(x)=0,可得x1=-ln 2>-1,x2=0,列表分析如下:
x (-1,-ln 2) -ln 2 (-ln 2,0) 0 (0,+∞)
g′(x) + 0 - 0 +
g(x) 增 极大值 减 极小值 增
可知g(x)min=g(-1)=g(0)=0,故函数的最小值为0.(5分)
(2) 证明:由(1)可知,当x>-1时,g(x)≥0,即≥1-x2(当且仅当x=0时取等号),
不妨取h(x)=1-x2,则在区间(-1,0)和(0,+∞)上,都有f(x)>h(x),
且h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,又由f′(x)=可知f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,且f(x)>0在(-1,0)和(0,+∞)上恒成立.(8分)
由x1≠x2,f(x1)=f(x2)=t,得0
而x3,4=±,所以|x1-x2|>2成立.(12分)
(
10
)
同课章节目录
