18.1.1平行四边形的性质 学案
图片预览



文档简介
中小学教育资源及组卷应用平台
18.1.1平行四边形的性质 导学案
课题 18.1.1平行四边形的性质 单元 第17单元 学科 数学 年级 八年级(下)
教材分析 理解并掌握平行四边形的相关概念和性质,培养学生初步应用这些知识解决问题的能力.学生亲自经历探索平行四边形有关概念和性质的过程,体会解决问题策略的多样性.
核心素养分析 经历探索平行四边形的有关概念和性质的过程, 发展学生的探究意识和合情推理的能力.通过探索、发现、论证培养学生类比、转化的数学思想方法,锻炼学生缜密的逻辑思维能力,渗透“转化”的数学思想.培养学生的推理论证能力和逻辑思维能力.
学习目标 1、在学生对平行四边形认识的原有基础上,进一步研究平行四边形的性质:平行四边形是中心对称图形,平行四边形的对边相等,对角相等.2、引导学生通过实践操作、探究发现平行四边形的性质,学会在实践中思考、观察、发现、培养学生的动手实践能力.
重点 平行四边形的性质:平行四边形是中心对称图形,平行四边形的对边平行且相等,对角相等.
难点 运用平行四边形的性质进行有关的论证和计算.
教学过程
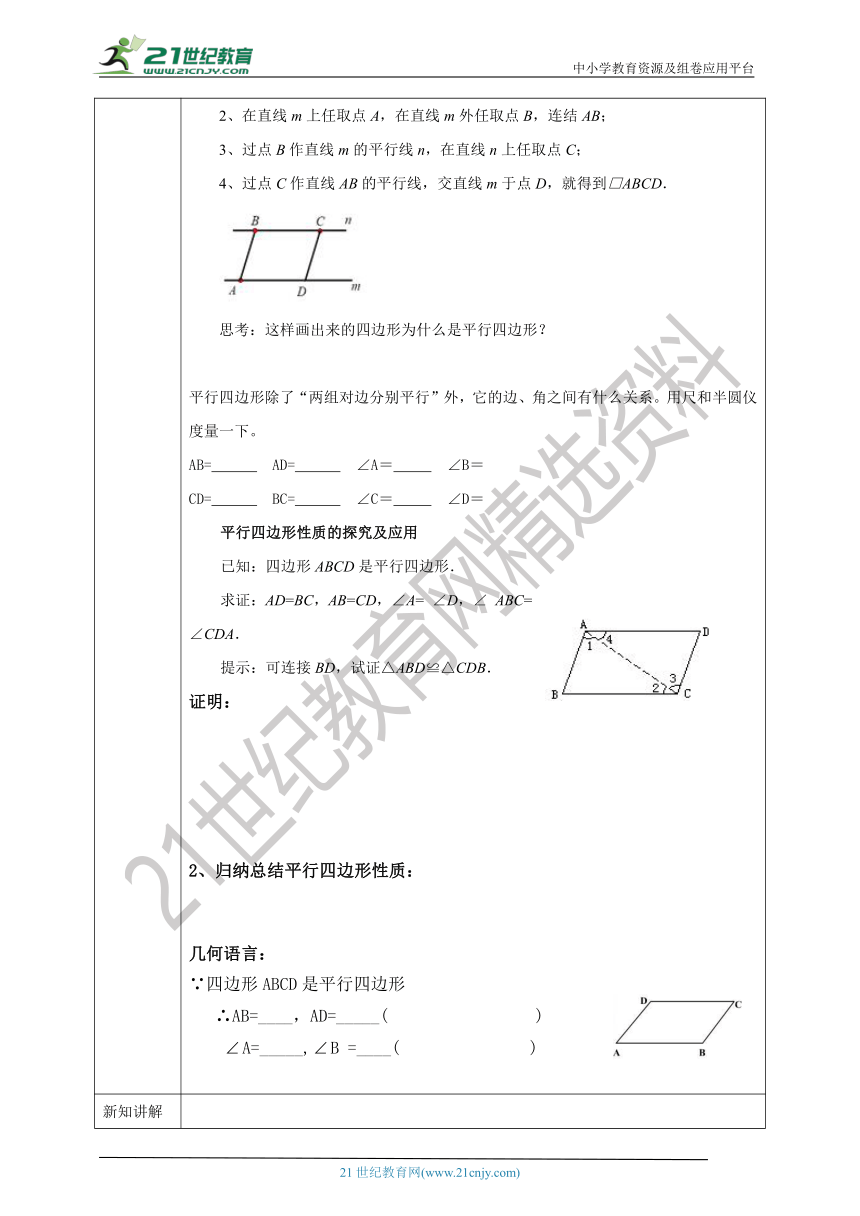
课前预学 引入思考创设情境,引入课题:引入: 在四边形中,最常见、价值最大的是平行四边形,如竹篱笆格子、推拉门、汽车防护链、书本等,都是平行四边形,(1)根据上述观察,请你用文字语言给平行四边形下个定义: 。 (2)请你用几何语言给平行四边形下个定义:∵ ∥ , ∥ ∴四边形ABCD是平行四边形3、平行四边形的数学符号是“ ”,平行四边形ABCD可以记作: 。试一试:如图,作一个平行四边形.步骤:1、任意画一条直线m;2、在直线m上任取点A,在直线m外任取点B,连结AB;3、过点B作直线m的平行线n,在直线n上任取点C;4、过点C作直线AB的平行线,交直线m于点D,就得到□ABCD.思考:这样画出来的四边形为什么是平行四边形?平行四边形除了“两组对边分别平行”外,它的边、角之间有什么关系。用尺和半圆仪度量一下。 AB= AD= ∠A= ∠B= CD= BC= ∠C= ∠D= 平行四边形性质的探究及应用已知:四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠A= ∠D,∠ ABC= ∠CDA.提示:可连接BD,试证△ABD≌△CDB.证明:2、归纳总结平行四边形性质 ( 21*cnjy*com ):21世纪教育网版权 几何语言:∵四边形ABCD是平行四边形 ∴AB=____,AD=_____( ) A=_____,B =____( )
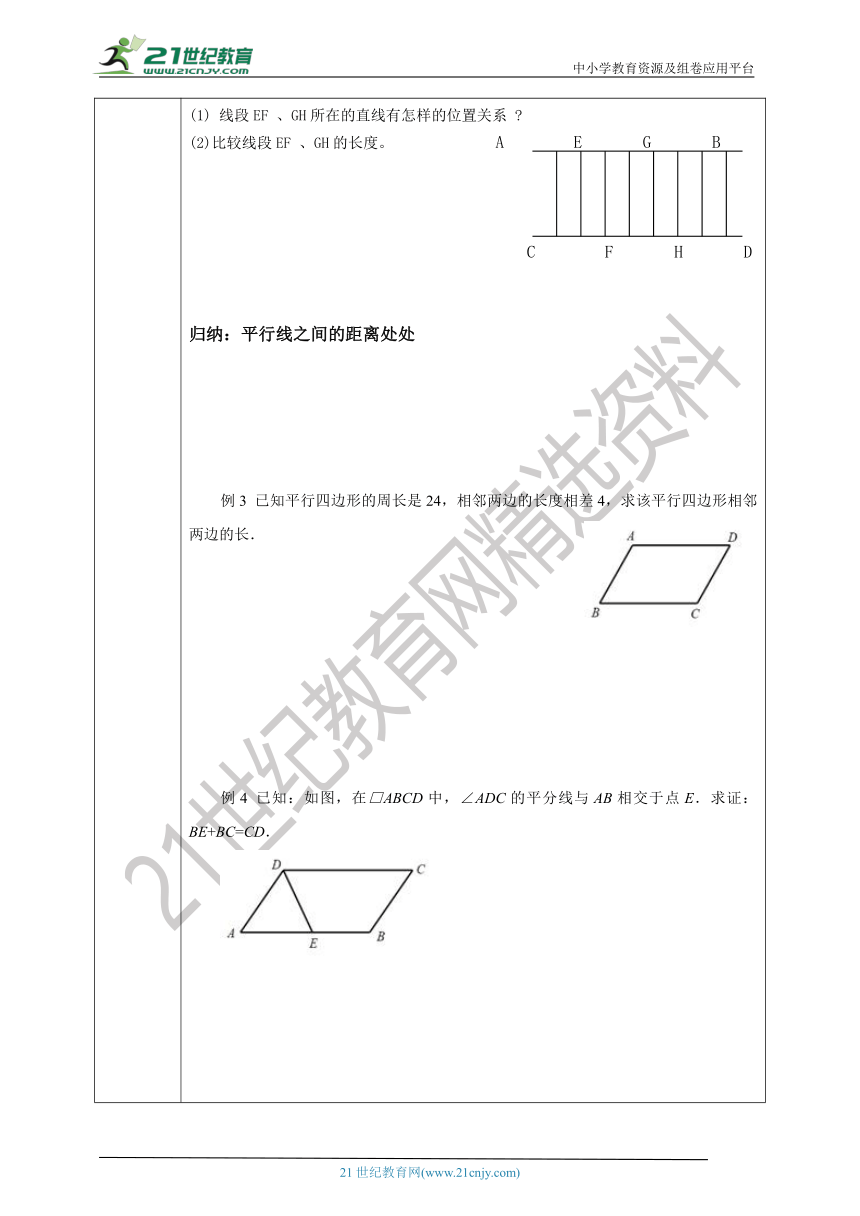
新知讲解 提炼概念归纳:平行四边形是中心对称图形.平行四边形的对边相等.平行四边形的对边平行.平行四边形的对角相等.平行四边形的邻角互补.平行四边形绕对角线的交点旋转180度后能与原图重合,所以说平行四边形是中心对称图形,对角线的交点就是对称中心.典例精讲 例1:如图,在平行四边形ABCD中,已知∠A=50°,你还能知道哪些角的度数?归纳:平行四边形的邻角 。21世纪教育网版权例2:如图,在平行四边形ABCD中 ( 21*cnjy*com ),已知AB=8,你还能知道哪些边的长?试一试:已知直线AB∥CD, 过直线AB上任意两点E 、G 分别向直线CD作垂线,交直线CD于点F、点H 。(1) 线段EF 、GH所在的直线有怎样的位置关系 (2)比较线段EF 、GH的长度。 A E G B C F H D归纳:平行线之间的距离处处 例3 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.例4 已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
课堂练习 巩固训练1.平行四边形具有而一般四边形不一定具有的特征是( )A、不稳定性 B、对边平行且相等C、内角的为360度 D、外角和为360度2.如图,在□ ABCD中, ∠B=110°,延长AD至点F,延长CD至点E,连结EF,则∠E+∠F的值为( )A.110° B.30° C.50° D.70°3.如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.4.在□ ABCD中,已知∠B-∠C= 80°,求∠D和∠A.5.如右图,AB=AC,且AB=5,从等腰三角形底边上任一点,分别作两腰的平行线,问:①四边形AEDF是什么图形?为什么?②图中∠1与∠B大小关系怎样?为什么? ∠2与∠3呢?③图中那些线段相等?为什么?④能否求□ AEDF的周长?答案引入思考平行四边形的表示法及相关概念如图:四边形ABCD是平行四边形.记作:□ABCD . 读作: 平行四边形ABCD .几何语言:∵ AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.平行四边形相对的边称为对边,相对的角称为对角.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.如图:线段AC、BD就是□ ABCD的对角线.注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.平行四边形性质的探究及应用已知:四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠A= ∠D,∠ ABC= ∠CDA.提示:可连接BD,试证△ABD≌△CDB.(作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.) 证明:连接AC,∵ AB∥CD,AD∥BC,∴ ∠1=∠3,∠2=∠4.21世纪教育网版权所又 AC=CA,∴ △ABC≌△CDA (ASA).∴ AB=CD,CB=AD,∠B=∠D.又 ∠1+∠4=∠2+∠3,∴ ∠BAD=∠BCD.21世提炼概念典例精讲 例1解:在□ABCD中, ∠A=∠C,∠B=∠D(平行四边形的对角相等).∵ ∠A=40°(已知),∴ ∠C=40°.又∵AD∥BC(平行四边形的对边平行),∴∠A+∠B=180°(两直线平行,同旁内角互补).∴∠B= 180 -∠A= 180 -40°=140 °,∠D=∠B=140 °.例2 解: 在□ ABCD中,AB=DC,AD=BC(平行四边形的对边相等).∵AB=8, ∴DC=8,又∵AB+BC+DC+AD=24,∴ AD=BC=4.例3解:设AB的长为x,则BC的长为x+4.根据已知,可得,2(AB + BC)=24,即2(x +x +4)=244 x +8 =24,解得x=4 .所以,该平行四边形相邻两边的长分别为4和8 .例4 解:∵四边形ABCD是平行四边形AB∥CD,AB=CD(平行四边形对边平行且相等)∴∠CDE=∠AED又∵DE是角平分线∴∠CDE=∠ADE∴∠AED=∠ADE∴AD=AE又∵AD=BC(平行四边形对边相等)∴AE=BC∴BE+BC=BE+AE=AB=CD。巩固训练1. B2. D 3. 124. 5.
课堂小结 1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.2、平行四边形的表示方法:平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD” .3、平行四边形的性质:(1)平行四边形是中心对称图形.(2)平行四边形的对边相等.平行四边形的对边平行.(3)平行四边形的对角相等.平行四边形的邻角互补.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
18.1.1平行四边形的性质 导学案
课题 18.1.1平行四边形的性质 单元 第17单元 学科 数学 年级 八年级(下)
教材分析 理解并掌握平行四边形的相关概念和性质,培养学生初步应用这些知识解决问题的能力.学生亲自经历探索平行四边形有关概念和性质的过程,体会解决问题策略的多样性.
核心素养分析 经历探索平行四边形的有关概念和性质的过程, 发展学生的探究意识和合情推理的能力.通过探索、发现、论证培养学生类比、转化的数学思想方法,锻炼学生缜密的逻辑思维能力,渗透“转化”的数学思想.培养学生的推理论证能力和逻辑思维能力.
学习目标 1、在学生对平行四边形认识的原有基础上,进一步研究平行四边形的性质:平行四边形是中心对称图形,平行四边形的对边相等,对角相等.2、引导学生通过实践操作、探究发现平行四边形的性质,学会在实践中思考、观察、发现、培养学生的动手实践能力.
重点 平行四边形的性质:平行四边形是中心对称图形,平行四边形的对边平行且相等,对角相等.
难点 运用平行四边形的性质进行有关的论证和计算.
教学过程
课前预学 引入思考创设情境,引入课题:引入: 在四边形中,最常见、价值最大的是平行四边形,如竹篱笆格子、推拉门、汽车防护链、书本等,都是平行四边形,(1)根据上述观察,请你用文字语言给平行四边形下个定义: 。 (2)请你用几何语言给平行四边形下个定义:∵ ∥ , ∥ ∴四边形ABCD是平行四边形3、平行四边形的数学符号是“ ”,平行四边形ABCD可以记作: 。试一试:如图,作一个平行四边形.步骤:1、任意画一条直线m;2、在直线m上任取点A,在直线m外任取点B,连结AB;3、过点B作直线m的平行线n,在直线n上任取点C;4、过点C作直线AB的平行线,交直线m于点D,就得到□ABCD.思考:这样画出来的四边形为什么是平行四边形?平行四边形除了“两组对边分别平行”外,它的边、角之间有什么关系。用尺和半圆仪度量一下。 AB= AD= ∠A= ∠B= CD= BC= ∠C= ∠D= 平行四边形性质的探究及应用已知:四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠A= ∠D,∠ ABC= ∠CDA.提示:可连接BD,试证△ABD≌△CDB.证明:2、归纳总结平行四边形性质 ( 21*cnjy*com ):21世纪教育网版权 几何语言:∵四边形ABCD是平行四边形 ∴AB=____,AD=_____( ) A=_____,B =____( )
新知讲解 提炼概念归纳:平行四边形是中心对称图形.平行四边形的对边相等.平行四边形的对边平行.平行四边形的对角相等.平行四边形的邻角互补.平行四边形绕对角线的交点旋转180度后能与原图重合,所以说平行四边形是中心对称图形,对角线的交点就是对称中心.典例精讲 例1:如图,在平行四边形ABCD中,已知∠A=50°,你还能知道哪些角的度数?归纳:平行四边形的邻角 。21世纪教育网版权例2:如图,在平行四边形ABCD中 ( 21*cnjy*com ),已知AB=8,你还能知道哪些边的长?试一试:已知直线AB∥CD, 过直线AB上任意两点E 、G 分别向直线CD作垂线,交直线CD于点F、点H 。(1) 线段EF 、GH所在的直线有怎样的位置关系 (2)比较线段EF 、GH的长度。 A E G B C F H D归纳:平行线之间的距离处处 例3 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.例4 已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
课堂练习 巩固训练1.平行四边形具有而一般四边形不一定具有的特征是( )A、不稳定性 B、对边平行且相等C、内角的为360度 D、外角和为360度2.如图,在□ ABCD中, ∠B=110°,延长AD至点F,延长CD至点E,连结EF,则∠E+∠F的值为( )A.110° B.30° C.50° D.70°3.如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.4.在□ ABCD中,已知∠B-∠C= 80°,求∠D和∠A.5.如右图,AB=AC,且AB=5,从等腰三角形底边上任一点,分别作两腰的平行线,问:①四边形AEDF是什么图形?为什么?②图中∠1与∠B大小关系怎样?为什么? ∠2与∠3呢?③图中那些线段相等?为什么?④能否求□ AEDF的周长?答案引入思考平行四边形的表示法及相关概念如图:四边形ABCD是平行四边形.记作:□ABCD . 读作: 平行四边形ABCD .几何语言:∵ AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.平行四边形相对的边称为对边,相对的角称为对角.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.如图:线段AC、BD就是□ ABCD的对角线.注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.平行四边形性质的探究及应用已知:四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠A= ∠D,∠ ABC= ∠CDA.提示:可连接BD,试证△ABD≌△CDB.(作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.) 证明:连接AC,∵ AB∥CD,AD∥BC,∴ ∠1=∠3,∠2=∠4.21世纪教育网版权所又 AC=CA,∴ △ABC≌△CDA (ASA).∴ AB=CD,CB=AD,∠B=∠D.又 ∠1+∠4=∠2+∠3,∴ ∠BAD=∠BCD.21世提炼概念典例精讲 例1解:在□ABCD中, ∠A=∠C,∠B=∠D(平行四边形的对角相等).∵ ∠A=40°(已知),∴ ∠C=40°.又∵AD∥BC(平行四边形的对边平行),∴∠A+∠B=180°(两直线平行,同旁内角互补).∴∠B= 180 -∠A= 180 -40°=140 °,∠D=∠B=140 °.例2 解: 在□ ABCD中,AB=DC,AD=BC(平行四边形的对边相等).∵AB=8, ∴DC=8,又∵AB+BC+DC+AD=24,∴ AD=BC=4.例3解:设AB的长为x,则BC的长为x+4.根据已知,可得,2(AB + BC)=24,即2(x +x +4)=244 x +8 =24,解得x=4 .所以,该平行四边形相邻两边的长分别为4和8 .例4 解:∵四边形ABCD是平行四边形AB∥CD,AB=CD(平行四边形对边平行且相等)∴∠CDE=∠AED又∵DE是角平分线∴∠CDE=∠ADE∴∠AED=∠ADE∴AD=AE又∵AD=BC(平行四边形对边相等)∴AE=BC∴BE+BC=BE+AE=AB=CD。巩固训练1. B2. D 3. 124. 5.
课堂小结 1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.2、平行四边形的表示方法:平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD” .3、平行四边形的性质:(1)平行四边形是中心对称图形.(2)平行四边形的对边相等.平行四边形的对边平行.(3)平行四边形的对角相等.平行四边形的邻角互补.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
