6.4.3正弦定理 课件(共17张PPT)
文档属性
| 名称 | 6.4.3正弦定理 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 716.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 11:57:13 | ||
图片预览


文档简介
(共17张PPT)
正弦定理(第1课时)
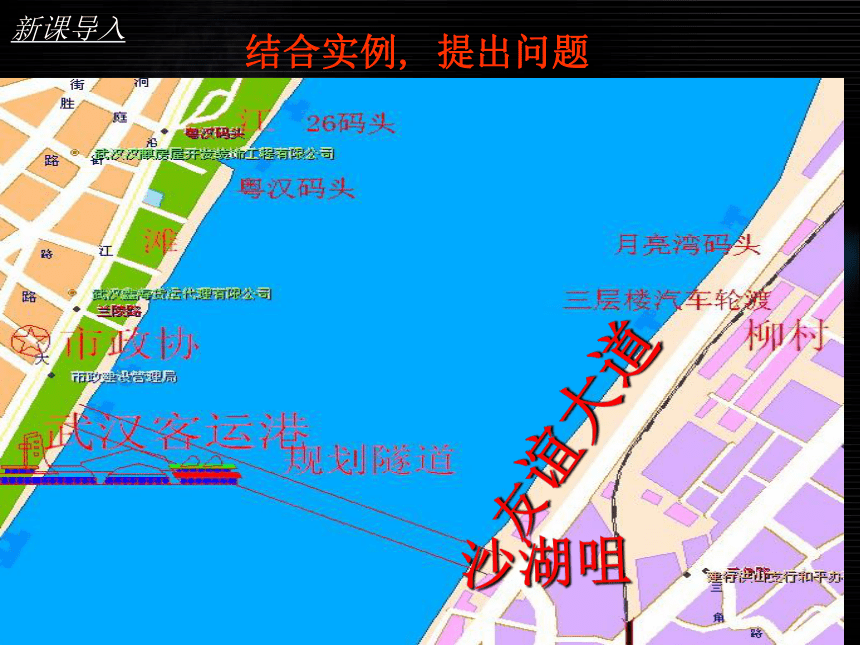
新课导入
结合实例, 提出问题
友谊大道
沙湖咀
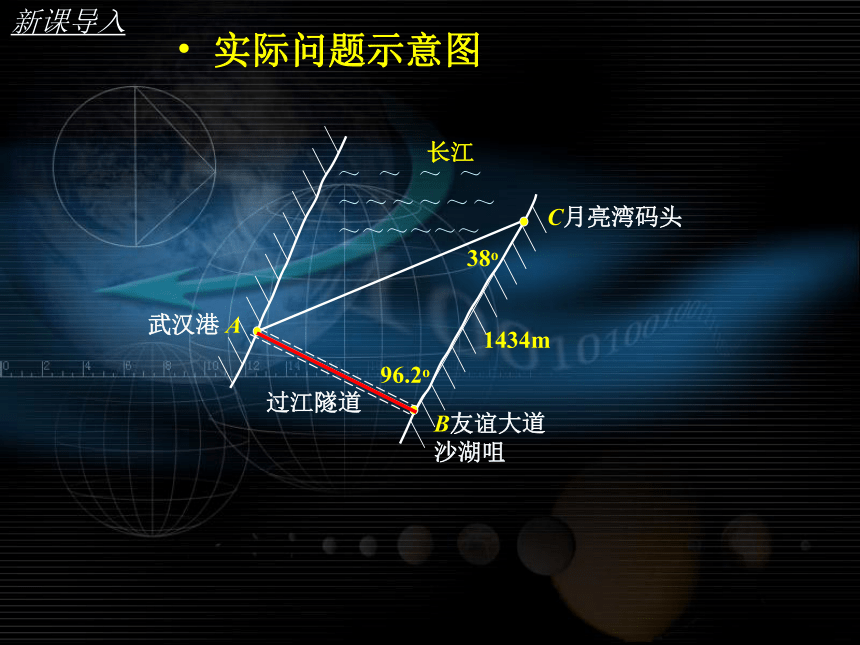
实际问题示意图
武汉港 A
B友谊大道
沙湖咀
C月亮湾码头
96.2o
38o
过江隧道
长江
~~~~
~~~~~~
~~~~~~
1434m
新课导入
96.2o
38o
武汉港A
B友谊大道
沙湖咀
C月亮湾码头
过江隧道
长江
~~~~
~~~~~~
~~~~~~
1434m
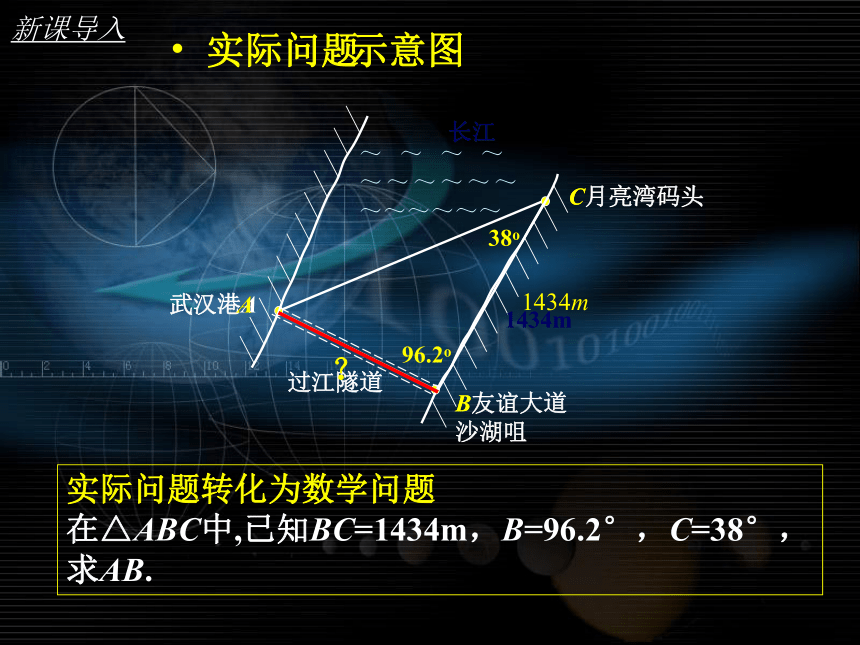
A
B
C
?
实际问题转化为数学问题
在△ABC中,已知BC=1434m,B=96.2°,C=38°,
求AB.
实际问题
示意图
新课导入
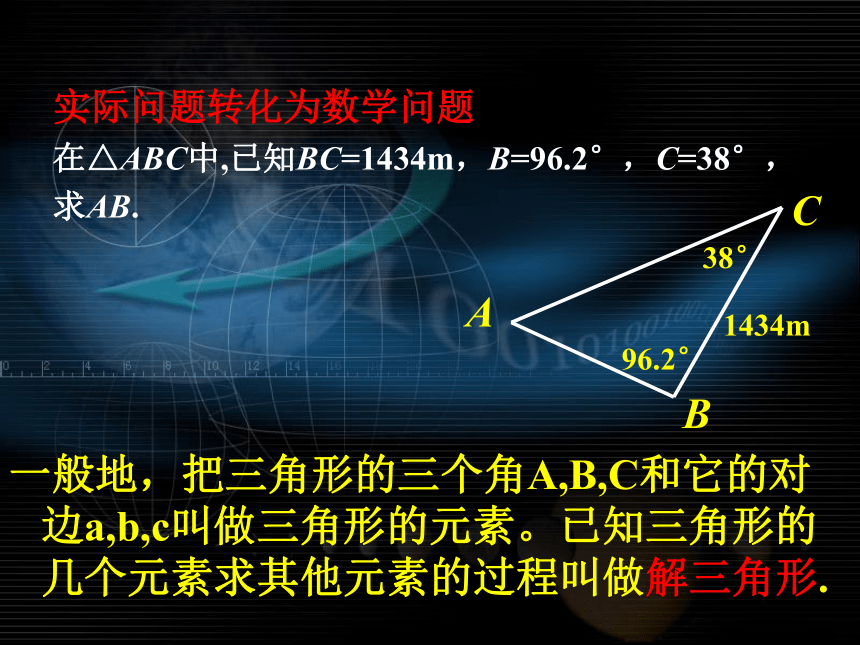
实际问题转化为数学问题
在△ABC中,已知BC=1434m,B=96.2°,C=38°,
求AB.
A
B
C
1434m
96.2°
38°
一般地,把三角形的三个角A,B,C和它的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形.
提出问题:
A
B
C
C
B
A
c
a
b
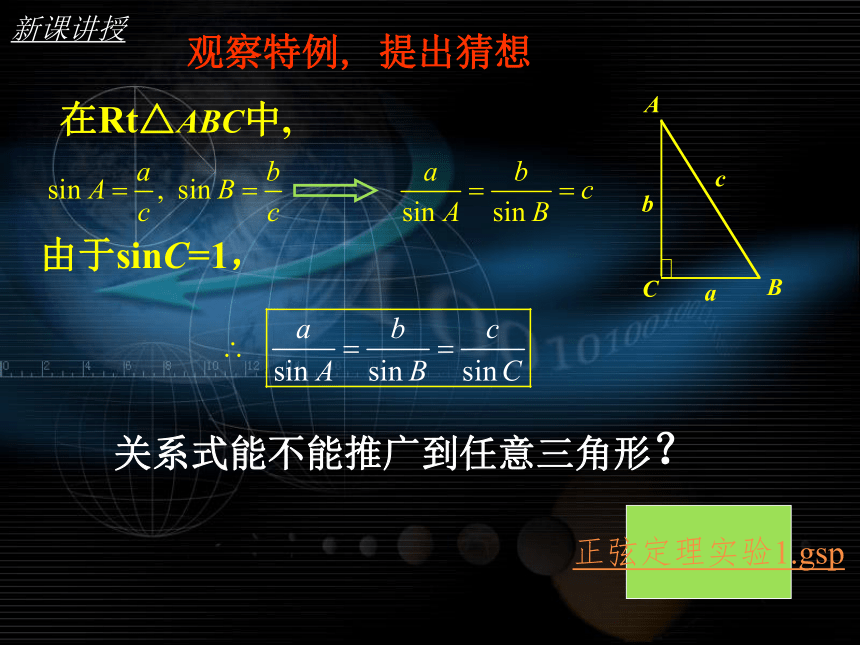
关系式能不能推广到任意三角形?
观察特例, 提出猜想
在Rt△ABC中,
新课讲授
由于sinC=1,
正弦定理实验1.gsp
关系式还能不能推广到钝角三角形?
继续探究, 证明猜想
在锐角三角形ABC中,作
新课讲授
A
B
C
D
E
a
c
b
再作CE⊥AB,得Rt△CBE和Rt△CAE,有
得Rt△ABD和Rt△ACD,有
深入探究, 证明猜想
在钝角三角形ABC中,
新课讲授
C
B
A
a
c
b
D
E
作CE⊥AB,则
再作AD⊥BC,得Rt△ABD和Rt△ACD,有
归纳总结,得出定理
新课讲授
正弦定理:在一个三角形中,各边和它 所对角的正弦的比相等,即
例1:在△ABC中,已知BC=1434m,B=96.2°C=38°,求AB.
A
B
C
1434m
96.2°
38°
解决导入实际问题
已知两角和任一边,求其他两边和一角
探究题
运用定理,解决问题
利用正弦定理,可以解决以下问题:
(1)已知两角和任一边,求其他两 边和一角;
(2)已知两边和其中一边的对角,求另一边的对角或其他的边、角.
课堂小结,巩固加深
正弦定理:在一个三角形中,各边和 它所对角的正弦的比相等,即
1、正弦定理揭示了任意三角形边角之间的关系,是解三角形的重要工具
正弦定理的证明
2、正弦定理解决的两类问题:
(1)已知两角和任一边,求其他两边和 一角;
(2)已知两边和其中一边的对角,求另一边的对角或其他的边、角;
注意讨论:一个解
两个解
无解
选做题
在△ABC中,
探求常数m与△ABC的关系.
课后探究
必做题
谢谢大家!
正弦定理(第1课时)
新课导入
结合实例, 提出问题
友谊大道
沙湖咀
实际问题示意图
武汉港 A
B友谊大道
沙湖咀
C月亮湾码头
96.2o
38o
过江隧道
长江
~~~~
~~~~~~
~~~~~~
1434m
新课导入
96.2o
38o
武汉港A
B友谊大道
沙湖咀
C月亮湾码头
过江隧道
长江
~~~~
~~~~~~
~~~~~~
1434m
A
B
C
?
实际问题转化为数学问题
在△ABC中,已知BC=1434m,B=96.2°,C=38°,
求AB.
实际问题
示意图
新课导入
实际问题转化为数学问题
在△ABC中,已知BC=1434m,B=96.2°,C=38°,
求AB.
A
B
C
1434m
96.2°
38°
一般地,把三角形的三个角A,B,C和它的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形.
提出问题:
A
B
C
C
B
A
c
a
b
关系式能不能推广到任意三角形?
观察特例, 提出猜想
在Rt△ABC中,
新课讲授
由于sinC=1,
正弦定理实验1.gsp
关系式还能不能推广到钝角三角形?
继续探究, 证明猜想
在锐角三角形ABC中,作
新课讲授
A
B
C
D
E
a
c
b
再作CE⊥AB,得Rt△CBE和Rt△CAE,有
得Rt△ABD和Rt△ACD,有
深入探究, 证明猜想
在钝角三角形ABC中,
新课讲授
C
B
A
a
c
b
D
E
作CE⊥AB,则
再作AD⊥BC,得Rt△ABD和Rt△ACD,有
归纳总结,得出定理
新课讲授
正弦定理:在一个三角形中,各边和它 所对角的正弦的比相等,即
例1:在△ABC中,已知BC=1434m,B=96.2°C=38°,求AB.
A
B
C
1434m
96.2°
38°
解决导入实际问题
已知两角和任一边,求其他两边和一角
探究题
运用定理,解决问题
利用正弦定理,可以解决以下问题:
(1)已知两角和任一边,求其他两 边和一角;
(2)已知两边和其中一边的对角,求另一边的对角或其他的边、角.
课堂小结,巩固加深
正弦定理:在一个三角形中,各边和 它所对角的正弦的比相等,即
1、正弦定理揭示了任意三角形边角之间的关系,是解三角形的重要工具
正弦定理的证明
2、正弦定理解决的两类问题:
(1)已知两角和任一边,求其他两边和 一角;
(2)已知两边和其中一边的对角,求另一边的对角或其他的边、角;
注意讨论:一个解
两个解
无解
选做题
在△ABC中,
探求常数m与△ABC的关系.
课后探究
必做题
谢谢大家!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
