第五章 三角函数 章末总结 课件(共48张PPT)
文档属性
| 名称 | 第五章 三角函数 章末总结 课件(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 11:58:13 | ||
图片预览











文档简介
(共48张PPT)
三角函数
规定:逆时针转动 ——正角
顺时针转动 ——负角
没有转动 ——零角
(1)角的顶点重合于原点;
(2)始边重合于x轴的非负半轴,
(3)终边落在第几象限就是第几象限角.
象限角
如果角的终边落在了坐标轴上,就认为这
个角不属于任何象限,也称非象限角
一般地,所有与角α终边相同的角,
连同角α在内所构成的集合S可以表示为
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
终边相同的角
思考:终边在x轴正半轴、负半轴,y轴正半轴、负半轴上的角分别如何表示?
x轴正半轴:α= k·360°,k∈Z ;
x轴负半轴:α= 180°+k·360°,k∈Z ;
y轴正半轴:α= 90°+k·360°,k∈Z ;
y轴负半轴:α= 270°+k·360°,k∈Z .
变式:请判断1305°是第几象限角;
方法一:解:1305°-1080°=225°
=3×360°+225°
方法二:解:1305°=1080°+225°
因为,1305°与225°终边相同
所以,1305°是第三象限的角
所以,1305°是第三象限的角
长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度记作rad.这种以弧度为单位来度量角的制度叫做弧度制.
注意:今后在用弧度制表示角的时候,弧度二字或rad可以略去不写.
弧度的定义:
360°=2 rad
180°= rad
1°
=
0.01745 rad
1 rad=
=57°18′
弧度制与角度制的换算:抓住关键
用弧度制表示弧长及扇形面积公式:
弧长公式:
扇形面积公式
其中l是扇形弧长,R是圆的半径.
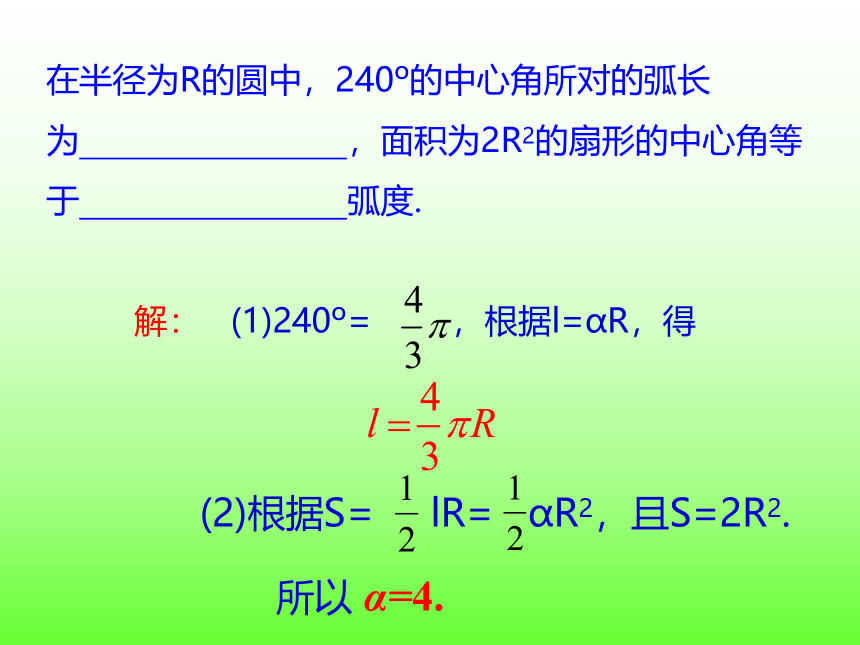
在半径为R的圆中,240 的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度.
解: (1)240 = ,根据l=αR,得
(2)根据S= lR= αR2,且S=2R2.
所以 α=4.
任意角的三角函数定义
设 是一个任意角,它的终边与单位圆交于点
那么:(1) 叫做 的正弦,记作 ,即 ;
(2) 叫做 的余弦,记作 ,即 ;
(3) 叫做 的正切,记作 ,即
那么① 叫做 的正弦,即
② 叫做 的余弦,即
③ 叫做 的正切,即
是终边上的任意一点,点 P 与原点的距离
于是,
1.变式: 1).已知角 的终边过点 ,
求 的三个三角函数值.
解:由已知可得:
终边相同的角的同一三角函数值相等(公式一)
其中
利用公式一,可以把求任意角的三角函数值,
转化为求 角的三角函数值 .
求下列三角函数值:
(1) . (2)
解:(1)
变式练习: 求下列三角函数值
(2)
根据三角函数的定义,当时 ,有
同角三角函数的基本关系:
由上可知:已知三角函数中的任意一个函数值,
必可求另外的两个函数值(知一求二)
奇变偶不变,符号看象限
对于公式一 ~ 六都叫做诱导公式.
【4】这些规律对任何三角函数(只要存在,有意义)都成立
【1】诱导公式都是α的三角函数与 的三角函数之间的
转化,记忆口诀是: 奇变偶不变,符号看象限
【2】“奇变偶不变”:
角α前面的是 ,如果k是奇数,那么得到的三角函数
名要发生变化,即 正弦变余弦,余弦变正弦;如果k是偶数,
那么得到的三角函数名不变化
【3】“符号看象限”:
将角α看成一个锐角(为了判断符号,实际α可以不是锐角),
此时判断 所在的象限,并观察原三角函数对这个角
运算得到的符号是正还是负.
的值为
A. B. C. 0 D.
2.已知,则的值等于 .
3.已知角的终边上有一点,则
的值为
A. B. C. D.
4.已知,
则________.
正弦函数的“五点画图法”
0
x
y
1
-1
●
●
●
●
●
y=sinx,x [0, 2 ]
五个关键点从左到右依次为:
余弦函数的“五点画图法”
o
x
y
●
●
●
●
●
1
-1
五个关键点从左到右依次为:
x
y
0
1
-1
sin( x+ )=
余弦函数y=cosx与正弦函数y=sinx的图象关系
cosx
y=sinx的图象
y=cosx的图象
正弦函数
定义域:R
值域:[-1,1]
余弦函数
为奇函数
为偶函数
周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f (x+T)=f (x)
那么函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期.
周期T中最小的正数叫做f (x)的最小正周期
正弦函数是周期函数,周期是 ,最小正周期是
余弦函数是周期函数,周期是 ,最小正周期是
练一练
(2)已知函数 的周期是3,且当 时, ,求
(1)求下列函数的最小正周期
①
②
f(1)=1+1=2
f(5)=f(5-3)=f(2)=2x2+1=5
f(16)=f(16-3x5)=f(1)=2
对称轴:
对称中心:
正弦函数
余弦函数
对称轴:
对称中心:
函数最值点
函数最值点
函数零点坐标
函数零点坐标
可以通过画草图找出
1.函数 的一条对称轴是( )
解:经验证,当
时
为对称轴
正弦函数的单调性
正弦函数在每个闭区间
上都是增函数,其值从-1增大到1;
而在每个闭区间
上都是
减函数,其值从1减小到-1。
余弦函数的单调性
余弦函数在每一个闭区间
上都是增函数,其值从-1增大到1 ;
上都是减函数,其值从1减小到-1。
而在每个闭区间
(1) ;
(2) .
解:(1)因为 ,
正弦函数y=sinx在区间 上单调递增,
所以
新知探究
不通过求值,比较下列各数的大小:
解:(2) ,
且余弦函数在区间[0,π]上单调递减,
所以
例 求函数 的单调递增区间.
解:令 ,则 .
因为 的单调递增区间是 ,
且由 得 ,
所以,函数 的
单调递增区间是 .
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
正余弦函数的最值
正弦函数
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
余弦函数
⑷ 奇偶性:
奇函数,图象关于原点对称。
⑵ 值域:
⑶ 周期性:
R
(6)单调性:
⑴ 定义域:
}
,
2
|
{
Z
k
k
x
x
+
p
p
在每一个开区间
上是增函数
正切函数y=tanx的性质
P(x,y) ·
P′ (-x,-y )·
(5) 对称性:
无对称轴
对称中心:
0
x
y
求(1)定义域:
(2)单调区间:
(3)周期
例2:不求值比较下列各组两个正切值的大小
又∵ 内单调递增
比较两个正切值大小,在同一单调区间内,利用单调递增性解决;如果所比较的两个值不在同一单调区间内,用诱导公式化到同一单调区间内。
符号上同下异
1.两角和与差的余弦公式:
2.两角和与差的正弦公式:
同名积,符号反
异名积,符号同
3.两角和与差的正切公式:
倍角公式
半角公式
辅助角公式:
注:解决复合三角函数的周期,最值等性质问题时,要化成单一名称的三角函数来解决.
求下列各式的值
求下列函数的周期,最大值和最小值
所以所求的周期为 ,最大值为2,最小值为-2
1
-1
2
-2
x
o
y
3
-3
2
y=sinx
y=sin(x- )①
②
③
以寻找“五点法”中的特殊点作为突破口:
“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;“第二点”(即图象的最高点)为ωx+φ= ;
“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;“第四点”(即图象的最低点)为ωx+φ= ;
“第五点”为ωx+φ=2π.
1.函数y=Asin(ωx+φ)中φ值的确定
总结:
利用 ,求得
选择的点要认清其属“五点法”中的哪一位置点,并能正确代人列式,求得 .
A:做简谐运动的物体离开平衡位置的最大距离,称为“振幅”.
当函数表示一个振动量时,
T:
f :
当函数表示一个振动量时:
称为“相位” .
x= 0时的相位 ,称为“初相”.
感谢观看
三角函数
规定:逆时针转动 ——正角
顺时针转动 ——负角
没有转动 ——零角
(1)角的顶点重合于原点;
(2)始边重合于x轴的非负半轴,
(3)终边落在第几象限就是第几象限角.
象限角
如果角的终边落在了坐标轴上,就认为这
个角不属于任何象限,也称非象限角
一般地,所有与角α终边相同的角,
连同角α在内所构成的集合S可以表示为
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
终边相同的角
思考:终边在x轴正半轴、负半轴,y轴正半轴、负半轴上的角分别如何表示?
x轴正半轴:α= k·360°,k∈Z ;
x轴负半轴:α= 180°+k·360°,k∈Z ;
y轴正半轴:α= 90°+k·360°,k∈Z ;
y轴负半轴:α= 270°+k·360°,k∈Z .
变式:请判断1305°是第几象限角;
方法一:解:1305°-1080°=225°
=3×360°+225°
方法二:解:1305°=1080°+225°
因为,1305°与225°终边相同
所以,1305°是第三象限的角
所以,1305°是第三象限的角
长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度记作rad.这种以弧度为单位来度量角的制度叫做弧度制.
注意:今后在用弧度制表示角的时候,弧度二字或rad可以略去不写.
弧度的定义:
360°=2 rad
180°= rad
1°
=
0.01745 rad
1 rad=
=57°18′
弧度制与角度制的换算:抓住关键
用弧度制表示弧长及扇形面积公式:
弧长公式:
扇形面积公式
其中l是扇形弧长,R是圆的半径.
在半径为R的圆中,240 的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度.
解: (1)240 = ,根据l=αR,得
(2)根据S= lR= αR2,且S=2R2.
所以 α=4.
任意角的三角函数定义
设 是一个任意角,它的终边与单位圆交于点
那么:(1) 叫做 的正弦,记作 ,即 ;
(2) 叫做 的余弦,记作 ,即 ;
(3) 叫做 的正切,记作 ,即
那么① 叫做 的正弦,即
② 叫做 的余弦,即
③ 叫做 的正切,即
是终边上的任意一点,点 P 与原点的距离
于是,
1.变式: 1).已知角 的终边过点 ,
求 的三个三角函数值.
解:由已知可得:
终边相同的角的同一三角函数值相等(公式一)
其中
利用公式一,可以把求任意角的三角函数值,
转化为求 角的三角函数值 .
求下列三角函数值:
(1) . (2)
解:(1)
变式练习: 求下列三角函数值
(2)
根据三角函数的定义,当时 ,有
同角三角函数的基本关系:
由上可知:已知三角函数中的任意一个函数值,
必可求另外的两个函数值(知一求二)
奇变偶不变,符号看象限
对于公式一 ~ 六都叫做诱导公式.
【4】这些规律对任何三角函数(只要存在,有意义)都成立
【1】诱导公式都是α的三角函数与 的三角函数之间的
转化,记忆口诀是: 奇变偶不变,符号看象限
【2】“奇变偶不变”:
角α前面的是 ,如果k是奇数,那么得到的三角函数
名要发生变化,即 正弦变余弦,余弦变正弦;如果k是偶数,
那么得到的三角函数名不变化
【3】“符号看象限”:
将角α看成一个锐角(为了判断符号,实际α可以不是锐角),
此时判断 所在的象限,并观察原三角函数对这个角
运算得到的符号是正还是负.
的值为
A. B. C. 0 D.
2.已知,则的值等于 .
3.已知角的终边上有一点,则
的值为
A. B. C. D.
4.已知,
则________.
正弦函数的“五点画图法”
0
x
y
1
-1
●
●
●
●
●
y=sinx,x [0, 2 ]
五个关键点从左到右依次为:
余弦函数的“五点画图法”
o
x
y
●
●
●
●
●
1
-1
五个关键点从左到右依次为:
x
y
0
1
-1
sin( x+ )=
余弦函数y=cosx与正弦函数y=sinx的图象关系
cosx
y=sinx的图象
y=cosx的图象
正弦函数
定义域:R
值域:[-1,1]
余弦函数
为奇函数
为偶函数
周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f (x+T)=f (x)
那么函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期.
周期T中最小的正数叫做f (x)的最小正周期
正弦函数是周期函数,周期是 ,最小正周期是
余弦函数是周期函数,周期是 ,最小正周期是
练一练
(2)已知函数 的周期是3,且当 时, ,求
(1)求下列函数的最小正周期
①
②
f(1)=1+1=2
f(5)=f(5-3)=f(2)=2x2+1=5
f(16)=f(16-3x5)=f(1)=2
对称轴:
对称中心:
正弦函数
余弦函数
对称轴:
对称中心:
函数最值点
函数最值点
函数零点坐标
函数零点坐标
可以通过画草图找出
1.函数 的一条对称轴是( )
解:经验证,当
时
为对称轴
正弦函数的单调性
正弦函数在每个闭区间
上都是增函数,其值从-1增大到1;
而在每个闭区间
上都是
减函数,其值从1减小到-1。
余弦函数的单调性
余弦函数在每一个闭区间
上都是增函数,其值从-1增大到1 ;
上都是减函数,其值从1减小到-1。
而在每个闭区间
(1) ;
(2) .
解:(1)因为 ,
正弦函数y=sinx在区间 上单调递增,
所以
新知探究
不通过求值,比较下列各数的大小:
解:(2) ,
且余弦函数在区间[0,π]上单调递减,
所以
例 求函数 的单调递增区间.
解:令 ,则 .
因为 的单调递增区间是 ,
且由 得 ,
所以,函数 的
单调递增区间是 .
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
正余弦函数的最值
正弦函数
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
余弦函数
⑷ 奇偶性:
奇函数,图象关于原点对称。
⑵ 值域:
⑶ 周期性:
R
(6)单调性:
⑴ 定义域:
}
,
2
|
{
Z
k
k
x
x
+
p
p
在每一个开区间
上是增函数
正切函数y=tanx的性质
P(x,y) ·
P′ (-x,-y )·
(5) 对称性:
无对称轴
对称中心:
0
x
y
求(1)定义域:
(2)单调区间:
(3)周期
例2:不求值比较下列各组两个正切值的大小
又∵ 内单调递增
比较两个正切值大小,在同一单调区间内,利用单调递增性解决;如果所比较的两个值不在同一单调区间内,用诱导公式化到同一单调区间内。
符号上同下异
1.两角和与差的余弦公式:
2.两角和与差的正弦公式:
同名积,符号反
异名积,符号同
3.两角和与差的正切公式:
倍角公式
半角公式
辅助角公式:
注:解决复合三角函数的周期,最值等性质问题时,要化成单一名称的三角函数来解决.
求下列各式的值
求下列函数的周期,最大值和最小值
所以所求的周期为 ,最大值为2,最小值为-2
1
-1
2
-2
x
o
y
3
-3
2
y=sinx
y=sin(x- )①
②
③
以寻找“五点法”中的特殊点作为突破口:
“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;“第二点”(即图象的最高点)为ωx+φ= ;
“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;“第四点”(即图象的最低点)为ωx+φ= ;
“第五点”为ωx+φ=2π.
1.函数y=Asin(ωx+φ)中φ值的确定
总结:
利用 ,求得
选择的点要认清其属“五点法”中的哪一位置点,并能正确代人列式,求得 .
A:做简谐运动的物体离开平衡位置的最大距离,称为“振幅”.
当函数表示一个振动量时,
T:
f :
当函数表示一个振动量时:
称为“相位” .
x= 0时的相位 ,称为“初相”.
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
