北师大版小学数学五年级下册《总复习--长方体和正方体》教学课件(共11张PPT)
文档属性
| 名称 | 北师大版小学数学五年级下册《总复习--长方体和正方体》教学课件(共11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
4. 长方体和正方体
北师大版小学数学五年级下册
总复习
学习目标
进一步体会长方体和正方体的基本特征,理解体积(容积)及其常用计量单位的意义,掌握长方体、正方体的体积和表面积的计算方法,能正确解答相关的简单实际问题。
教学重点
(1)在观察、比较、实验等活动中,体会并理解体积和容积的意义;
(2)密切联系生活实际,感受体积、容积单位的实际意义。
教学难点
探究长方体、正方体体积的计算方法及不规则物体体积的测量方法。
考点1:
长方体的体积=长×宽×高,字母公式为V =abh。
正方体的体积=棱长×棱长×棱长,字母公式为V =。
长方体(或正方体)的体积=底面积×高,字母公式为V =Sh。
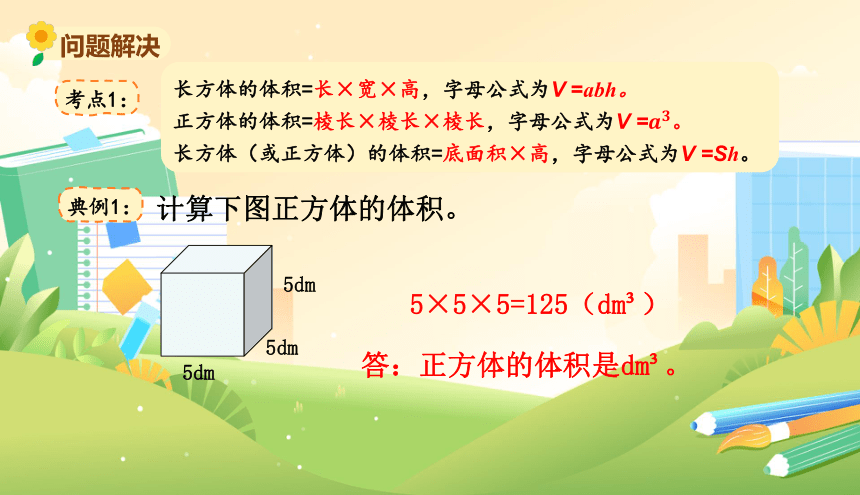
典例1:
计算下图正方体的体积。
5dm
5dm
5dm
5×5×5=125(dm )
答:正方体的体积是dm 。
考点1:
典例2:
张阿姨家有一个长方体形状的水箱(水箱厚度忽略不计),可装240L水。这个水箱长1.2m、宽0.4m,求这个水箱有多高。
0.24÷(1.2×0.4)=0.5(m)
答:这个水箱高0.5米。
240 L=240 dm =0.24 m
长方体的体积=长×宽×高,字母公式为V =abh。
正方体的体积=棱长×棱长×棱长,字母公式为V =。
长方体(或正方体)的体积=底面积×高,字母公式为V =Sh。
考点2:
长方体的表面积=(长×宽+长×高+宽×高)×2,用字母表示为S =2(ab+ah+bh)
正方体的表面积=棱长×棱长×6,用字母表示为S =6
计算下面长方体的表面积。
1×6×4+1×1×2=26(m )
1m
6m
1m
典例:
考点3:
典例:
1=1000, 1=1000c。
1L=1000mL 1000mL=1L
1L=1 1mL=1
5=( )
9000=( )。
5000
9
高级单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率。
填空。
(1)一个正方体的棱长是8dm,它的棱长总和是( )dm,
表面积是( ),体积是( )。
(2)如果一个正方体的底面积是25,那么它的表面
积是( ),体积是( )。
(3)一个正方体的每条棱长都扩大到原来的2倍,它的体
积就扩大到原来的( )倍,表面积就扩大到原来
的( )倍。
96
384
512
150
125
8
4
判断。
(1)长方体的三条棱分别叫作它的长、宽、高。 ( )
(2)棱长为6dm的正方体,表面积和体积相等。 ( )
(3)用两根同样长的铁丝分别围成一个长方体和一个正方体框
架,正方体框架的体积大于长方体框架的体积。 ( )
(4)体积相等的两个长方体,它们的表面积一定相等。( )
×
×
×
√
(2)一个长方体的高缩小到原来的,要使它的体积发生变化,
则( )。
(1)把一个长方体分成几个小长方体后,小长方体的体积和原
长方体的体积相比较,( )。
选择。
B
A
A.不变 B.比原来小了 C.比原来大了 D.无法确定
A.底面积扩大到原来的2倍 B.长和宽都扩大到原来的2倍
C.长不变,宽扩大到原来的2倍 D.宽不变,长扩大到原来的2倍
完成课本第96页 第3、4、5题。
4. 长方体和正方体
北师大版小学数学五年级下册
总复习
学习目标
进一步体会长方体和正方体的基本特征,理解体积(容积)及其常用计量单位的意义,掌握长方体、正方体的体积和表面积的计算方法,能正确解答相关的简单实际问题。
教学重点
(1)在观察、比较、实验等活动中,体会并理解体积和容积的意义;
(2)密切联系生活实际,感受体积、容积单位的实际意义。
教学难点
探究长方体、正方体体积的计算方法及不规则物体体积的测量方法。
考点1:
长方体的体积=长×宽×高,字母公式为V =abh。
正方体的体积=棱长×棱长×棱长,字母公式为V =。
长方体(或正方体)的体积=底面积×高,字母公式为V =Sh。
典例1:
计算下图正方体的体积。
5dm
5dm
5dm
5×5×5=125(dm )
答:正方体的体积是dm 。
考点1:
典例2:
张阿姨家有一个长方体形状的水箱(水箱厚度忽略不计),可装240L水。这个水箱长1.2m、宽0.4m,求这个水箱有多高。
0.24÷(1.2×0.4)=0.5(m)
答:这个水箱高0.5米。
240 L=240 dm =0.24 m
长方体的体积=长×宽×高,字母公式为V =abh。
正方体的体积=棱长×棱长×棱长,字母公式为V =。
长方体(或正方体)的体积=底面积×高,字母公式为V =Sh。
考点2:
长方体的表面积=(长×宽+长×高+宽×高)×2,用字母表示为S =2(ab+ah+bh)
正方体的表面积=棱长×棱长×6,用字母表示为S =6
计算下面长方体的表面积。
1×6×4+1×1×2=26(m )
1m
6m
1m
典例:
考点3:
典例:
1=1000, 1=1000c。
1L=1000mL 1000mL=1L
1L=1 1mL=1
5=( )
9000=( )。
5000
9
高级单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率。
填空。
(1)一个正方体的棱长是8dm,它的棱长总和是( )dm,
表面积是( ),体积是( )。
(2)如果一个正方体的底面积是25,那么它的表面
积是( ),体积是( )。
(3)一个正方体的每条棱长都扩大到原来的2倍,它的体
积就扩大到原来的( )倍,表面积就扩大到原来
的( )倍。
96
384
512
150
125
8
4
判断。
(1)长方体的三条棱分别叫作它的长、宽、高。 ( )
(2)棱长为6dm的正方体,表面积和体积相等。 ( )
(3)用两根同样长的铁丝分别围成一个长方体和一个正方体框
架,正方体框架的体积大于长方体框架的体积。 ( )
(4)体积相等的两个长方体,它们的表面积一定相等。( )
×
×
×
√
(2)一个长方体的高缩小到原来的,要使它的体积发生变化,
则( )。
(1)把一个长方体分成几个小长方体后,小长方体的体积和原
长方体的体积相比较,( )。
选择。
B
A
A.不变 B.比原来小了 C.比原来大了 D.无法确定
A.底面积扩大到原来的2倍 B.长和宽都扩大到原来的2倍
C.长不变,宽扩大到原来的2倍 D.宽不变,长扩大到原来的2倍
完成课本第96页 第3、4、5题。
