7.3万有引力理论的成就 课件(共18张PPT)
文档属性
| 名称 | 7.3万有引力理论的成就 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-28 16:24:55 | ||
图片预览



文档简介
第3节万有引力的成就
年 级:高一
学 科:物理(人教版)
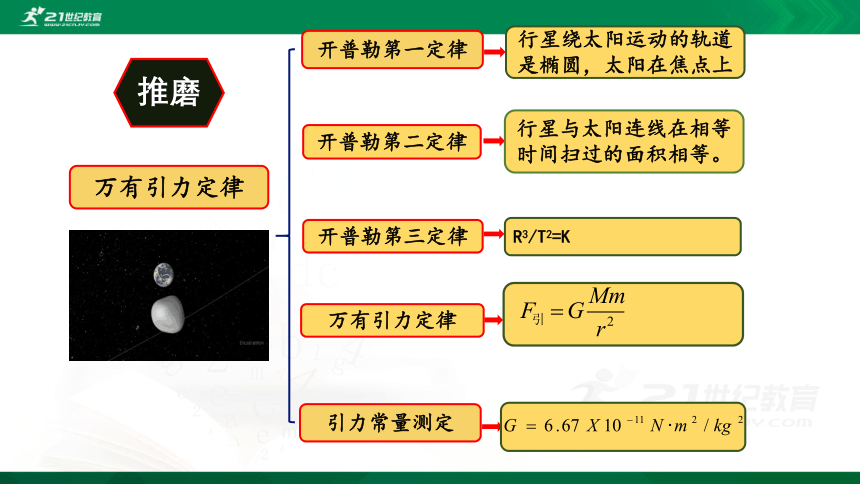
万有引力定律
推磨
开普勒第一定律
开普勒第二定律
万有引力定律
开普勒第三定律
行星绕太阳运动的轨道是椭圆,太阳在焦点上
行星与太阳连线在相等时间扫过的面积相等。
R3/T2=K
引力常量测定
第6章 圆周运动
一、“称量”一些大家伙
我们已经知道物体的质量可以用天平来测量,生活中物体的质量常用电子秤或台秤来称量。
但是对于地球、太阳等星体这种庞然大物,我们又该如何去“称量”它们的质量呢?
第6章 圆周运动
一、“称量”一些大家伙
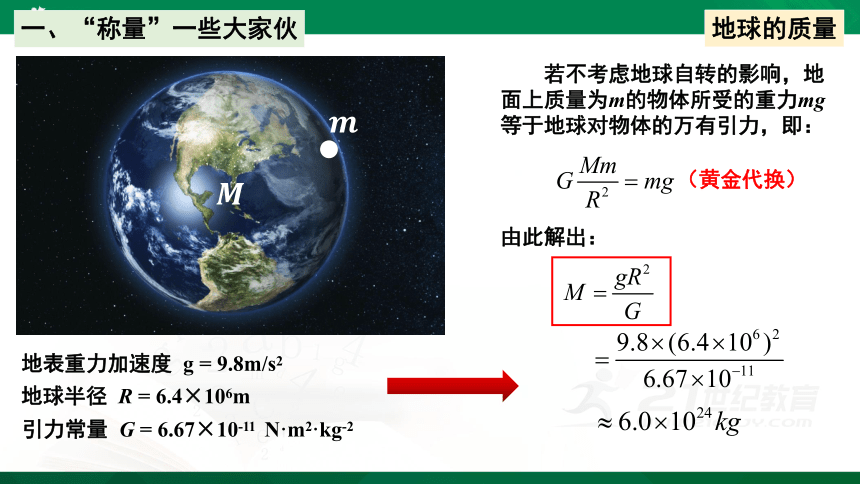
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的万有引力,即:
地球的质量
????
?
????
?
由此解出:
地球半径 R = 6.4×106m
地表重力加速度 g = 9.8m/s2
引力常量 G = 6.67×10-11 N·m2·kg-2
(黄金代换)
第6章 圆周运动
一、“称量”一些大家伙
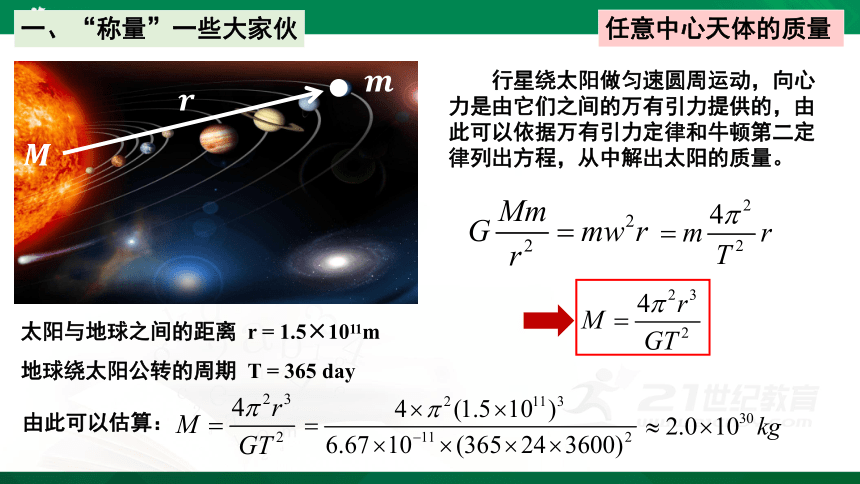
行星绕太阳做匀速圆周运动,向心力是由它们之间的万有引力提供的,由此可以依据万有引力定律和牛顿第二定律列出方程,从中解出太阳的质量。
任意中心天体的质量
由此可以估算:
????
?
????
?
????
?
太阳与地球之间的距离 r = 1.5×1011m
地球绕太阳公转的周期 T = 365 day
一、“称量”一些大家伙
虽然不同行星与太阳间的距离r和绕太阳公转的周期T各不相同,但是根据开普勒第三定律,所有行星的均相同,所以无论选择哪颗行星的轨道半径和公转周期进行计算,所得的太阳质量均相同。
任意中心天体的质量
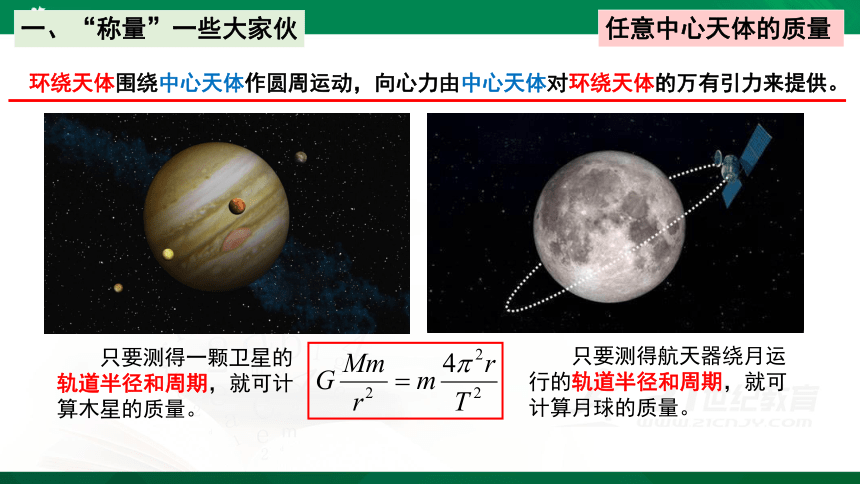
环绕天体围绕中心天体作圆周运动,向心力由中心天体对环绕天体的万有引力来提供。
r
F
环绕天体m
中心天体M
注意:此种方法估算的是中心天体的质量,而非是环绕天体的质量。
一、“称量”一些大家伙
任意中心天体的质量
环绕天体围绕中心天体作圆周运动,向心力由中心天体对环绕天体的万有引力来提供。
只要测得一颗卫星的轨道半径和周期,就可计算木星的质量。
只要测得航天器绕月运行的轨道半径和周期,就可计算月球的质量。
当估算出中心天体的质量后,是否可以估算出中心天体的球体密度?如何来估算?
(1)已知球体体积公式为:
(2)密度公式为:
????=?????????????????????
?
????=????????
?
二、估算天体的密度
????=????????=????????????????????????????????????=????????????????????????
?
????=????????????????
?
若
则
当估算出中心天体的质量后,是否可以估算出中心天体的球体密度?如何来估算?
(1)已知球体体积公式为:
(2)密度公式为:
????=?????????????????????
?
????=????????
?
????=????????=????????????????????????????????????????????????????=????????????????????????????????????
?
????=????????????????????????????????
?
若
则
二、估算天体的密度
三、笔尖下发现的行星
到了18世纪,人们已经知道太阳系有7颗行星,其中1781年发现的第七颗行星——天王星的运动轨道有些“古怪”:根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。
是天文观测数据不准确?
是万有引力定律的准确性有问题?
是天王星轨道外面还有一颗未发现的行星?
……
1846年9月23日晚,德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。后来,这颗行星被命名为海王星。
三、笔尖下发现的行星
海王星的轨道之外残存着太阳系形成初期遗留的物质,近100年来,人们在这里发现了冥王星、阋神星等几个较大的天体。
但是因为距离遥远,太阳的光芒到达那里已经十分微弱了,在地球附近很难看出究竟。尽管如此,黑暗寒冷的太阳系边缘依然牵动着人们的心,探索工作从来没有停止过。
冥王星
阋神星
四、预言哈雷彗星回归
英国天文学家哈雷从1337年到1698年的彗星记录中挑选了24颗彗星,依据万有引力定律,用一年时间计算了它们的轨道。
哈雷发现1531年、1607年和1682年出现的这三颗彗星轨道看起来如出一辙,他预言这三次出现的彗星是同一颗星,周期约为76年,并预言它将于1758年底或1759年初再次回归。
哈雷彗星回归周期
1759年3月这颗彗星如期通过了近日点,它最近一次回归是1986年,它的下次回归将在2061年左右。
五、潮汐现象
牛顿还用月球和太阳的万有引力解释了潮汐现象,用万有引力定律和其他力学定律,推测地球呈赤道处略为隆起的扁平形状。
潮汐,是发生在沿海地区的一种自然现象,是指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动。习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流。
六、练习与应用
教材第58页 第1题
1. 已知月球的质量是7.3×10 kg,半径是 1.7×10 km。
22
3
(1)月球表面的自由落体加速度有多大?
(2)这对宇航员在月球表面的行走会产生什么影响?
(3)若宇航员在地面上最多能举起质量为m的物体,他在月球表面最多能举起质量是多少的物体?
解:(1)
(2)
在月球上人行走起来会感觉很轻松,习惯在地球表面上行走的人,在月球表面行走时都是跳跃前进的。
(3)
最多能够举起6m的物体。
六、练习与应用
教材第58页 第2题
2. 根据万有引力定律和牛顿第二定律说明:为什么不同物体在地球表面的自由落体加速度都是相等的?为什么高山上的自由落体加速度比山下地面的小?
因为在地球表面,对于质量为m的物体有:
对于质量不同的物体,得到的结果是一致的,即与物体本身的质量m无关。
根据万有引力定律有:
高山的r较大,所以在高山上的重力加速度g较小。
解:
六、练习与应用
教材第58页 第3题
3. 某人造地球卫星沿圆轨道运行,轨道半径是6.8×10 km,周期是5.6×10 s。试从这些数据估算地球的质量。
3
3
卫星绕地球做圆周运动的向心力由地球对卫星的万有引力来提供,故有:
解:
六、练习与应用
教材第58页 第4题
4. 地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷成功预言哈雷彗星的回归,哈雷彗星最近出现的时间是1986年,预测下次飞近地球将在2061年。
(1)根据开普勒行星运动定律估算哈雷彗星轨道的半长轴是地球公转半径的多少倍?
解:(1)
根据开普勒第三定律有:
六、练习与应用
教材第58页 第4题
4. 地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷成功预言哈雷彗星的回归,哈雷彗星最近出现的时间是1986年,预测下次飞近地球将在2061年。
(2)若哈雷彗星在近日点与太阳中心的距离为r1,线速度大小为v1;在远日点与太阳中心的距离为r2,线速度大小为v2,请比较哪个速度大,并求得哈雷彗星在近日点和远日点的加速度大小之比。
解:(2)
根据开普勒第二定律有:
彗星在近日点的速度大于远日点的速度,即 。
由万有引力定律和牛顿第二定律有:
年 级:高一
学 科:物理(人教版)
万有引力定律
推磨
开普勒第一定律
开普勒第二定律
万有引力定律
开普勒第三定律
行星绕太阳运动的轨道是椭圆,太阳在焦点上
行星与太阳连线在相等时间扫过的面积相等。
R3/T2=K
引力常量测定
第6章 圆周运动
一、“称量”一些大家伙
我们已经知道物体的质量可以用天平来测量,生活中物体的质量常用电子秤或台秤来称量。
但是对于地球、太阳等星体这种庞然大物,我们又该如何去“称量”它们的质量呢?
第6章 圆周运动
一、“称量”一些大家伙
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的万有引力,即:
地球的质量
????
?
????
?
由此解出:
地球半径 R = 6.4×106m
地表重力加速度 g = 9.8m/s2
引力常量 G = 6.67×10-11 N·m2·kg-2
(黄金代换)
第6章 圆周运动
一、“称量”一些大家伙
行星绕太阳做匀速圆周运动,向心力是由它们之间的万有引力提供的,由此可以依据万有引力定律和牛顿第二定律列出方程,从中解出太阳的质量。
任意中心天体的质量
由此可以估算:
????
?
????
?
????
?
太阳与地球之间的距离 r = 1.5×1011m
地球绕太阳公转的周期 T = 365 day
一、“称量”一些大家伙
虽然不同行星与太阳间的距离r和绕太阳公转的周期T各不相同,但是根据开普勒第三定律,所有行星的均相同,所以无论选择哪颗行星的轨道半径和公转周期进行计算,所得的太阳质量均相同。
任意中心天体的质量
环绕天体围绕中心天体作圆周运动,向心力由中心天体对环绕天体的万有引力来提供。
r
F
环绕天体m
中心天体M
注意:此种方法估算的是中心天体的质量,而非是环绕天体的质量。
一、“称量”一些大家伙
任意中心天体的质量
环绕天体围绕中心天体作圆周运动,向心力由中心天体对环绕天体的万有引力来提供。
只要测得一颗卫星的轨道半径和周期,就可计算木星的质量。
只要测得航天器绕月运行的轨道半径和周期,就可计算月球的质量。
当估算出中心天体的质量后,是否可以估算出中心天体的球体密度?如何来估算?
(1)已知球体体积公式为:
(2)密度公式为:
????=?????????????????????
?
????=????????
?
二、估算天体的密度
????=????????=????????????????????????????????????=????????????????????????
?
????=????????????????
?
若
则
当估算出中心天体的质量后,是否可以估算出中心天体的球体密度?如何来估算?
(1)已知球体体积公式为:
(2)密度公式为:
????=?????????????????????
?
????=????????
?
????=????????=????????????????????????????????????????????????????=????????????????????????????????????
?
????=????????????????????????????????
?
若
则
二、估算天体的密度
三、笔尖下发现的行星
到了18世纪,人们已经知道太阳系有7颗行星,其中1781年发现的第七颗行星——天王星的运动轨道有些“古怪”:根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。
是天文观测数据不准确?
是万有引力定律的准确性有问题?
是天王星轨道外面还有一颗未发现的行星?
……
1846年9月23日晚,德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。后来,这颗行星被命名为海王星。
三、笔尖下发现的行星
海王星的轨道之外残存着太阳系形成初期遗留的物质,近100年来,人们在这里发现了冥王星、阋神星等几个较大的天体。
但是因为距离遥远,太阳的光芒到达那里已经十分微弱了,在地球附近很难看出究竟。尽管如此,黑暗寒冷的太阳系边缘依然牵动着人们的心,探索工作从来没有停止过。
冥王星
阋神星
四、预言哈雷彗星回归
英国天文学家哈雷从1337年到1698年的彗星记录中挑选了24颗彗星,依据万有引力定律,用一年时间计算了它们的轨道。
哈雷发现1531年、1607年和1682年出现的这三颗彗星轨道看起来如出一辙,他预言这三次出现的彗星是同一颗星,周期约为76年,并预言它将于1758年底或1759年初再次回归。
哈雷彗星回归周期
1759年3月这颗彗星如期通过了近日点,它最近一次回归是1986年,它的下次回归将在2061年左右。
五、潮汐现象
牛顿还用月球和太阳的万有引力解释了潮汐现象,用万有引力定律和其他力学定律,推测地球呈赤道处略为隆起的扁平形状。
潮汐,是发生在沿海地区的一种自然现象,是指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动。习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流。
六、练习与应用
教材第58页 第1题
1. 已知月球的质量是7.3×10 kg,半径是 1.7×10 km。
22
3
(1)月球表面的自由落体加速度有多大?
(2)这对宇航员在月球表面的行走会产生什么影响?
(3)若宇航员在地面上最多能举起质量为m的物体,他在月球表面最多能举起质量是多少的物体?
解:(1)
(2)
在月球上人行走起来会感觉很轻松,习惯在地球表面上行走的人,在月球表面行走时都是跳跃前进的。
(3)
最多能够举起6m的物体。
六、练习与应用
教材第58页 第2题
2. 根据万有引力定律和牛顿第二定律说明:为什么不同物体在地球表面的自由落体加速度都是相等的?为什么高山上的自由落体加速度比山下地面的小?
因为在地球表面,对于质量为m的物体有:
对于质量不同的物体,得到的结果是一致的,即与物体本身的质量m无关。
根据万有引力定律有:
高山的r较大,所以在高山上的重力加速度g较小。
解:
六、练习与应用
教材第58页 第3题
3. 某人造地球卫星沿圆轨道运行,轨道半径是6.8×10 km,周期是5.6×10 s。试从这些数据估算地球的质量。
3
3
卫星绕地球做圆周运动的向心力由地球对卫星的万有引力来提供,故有:
解:
六、练习与应用
教材第58页 第4题
4. 地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷成功预言哈雷彗星的回归,哈雷彗星最近出现的时间是1986年,预测下次飞近地球将在2061年。
(1)根据开普勒行星运动定律估算哈雷彗星轨道的半长轴是地球公转半径的多少倍?
解:(1)
根据开普勒第三定律有:
六、练习与应用
教材第58页 第4题
4. 地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷成功预言哈雷彗星的回归,哈雷彗星最近出现的时间是1986年,预测下次飞近地球将在2061年。
(2)若哈雷彗星在近日点与太阳中心的距离为r1,线速度大小为v1;在远日点与太阳中心的距离为r2,线速度大小为v2,请比较哪个速度大,并求得哈雷彗星在近日点和远日点的加速度大小之比。
解:(2)
根据开普勒第二定律有:
彗星在近日点的速度大于远日点的速度,即 。
由万有引力定律和牛顿第二定律有:
