华师版数学八年级下册第17章 函数及其图象 章末复习课件(共31张PPT)
文档属性
| 名称 | 华师版数学八年级下册第17章 函数及其图象 章末复习课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 770.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 22:39:18 | ||
图片预览








文档简介
(共31张PPT)
章末复习
华东师大·八年级数学下册
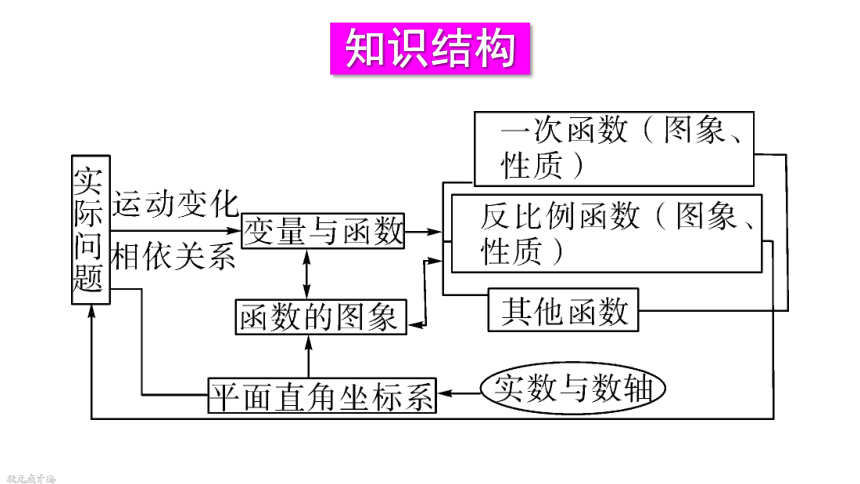
知识结构
知识回顾
1.函数的概念
变量:变化过程中可以取不同数值的量.
常量:变化过程中保持不变的量.
函数:如果在一个变化过程中,有两个变量x和y,对于每一个x值,y都有惟一的值和它对应,我们就说x是自变量,y是因变量,y是x的函数.
2.如何求函数的自变量取值范围
考虑两个方面,其一是分母不等于0,其二是开偶次方的被开方数为非负数,对于实际问题,应根据具体情况而定.
3.关于平面直角坐标系
平面上的点与有序实数对成一一对应关系,其含义是坐标平面上的每一个点都可以用一对有序实数来表示,反过来,每一对有序实数都可以在坐标平面上描出一点,这样数与形就有机地结合在一起.我们可以在平面上建立直角坐标系定出点的位置.
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
A
F
D
C
B
E
+
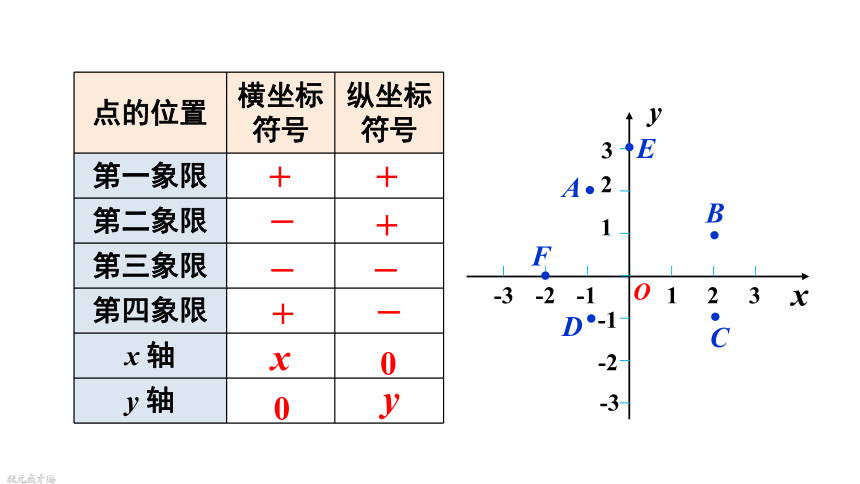
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x 轴
y 轴
+
-
+
-
-
+
-
x
0
0
y
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
Ⅰ
Ⅱ
Ⅲ
Ⅳ
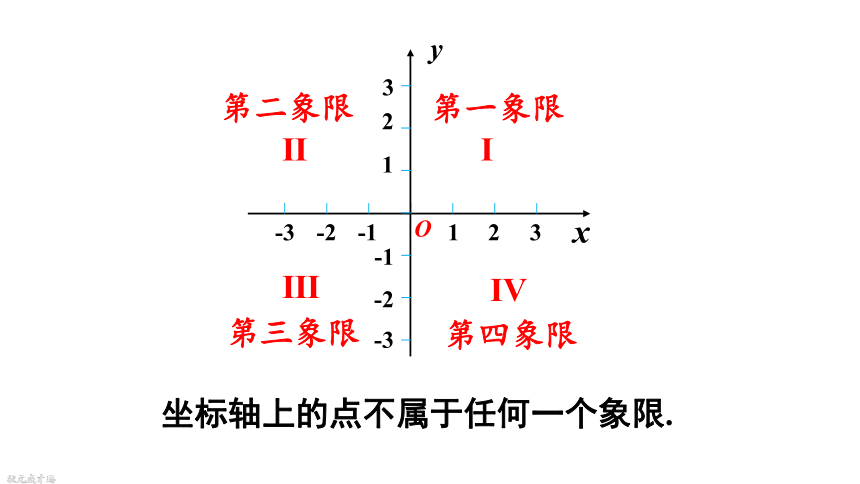
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不属于任何一个象限.
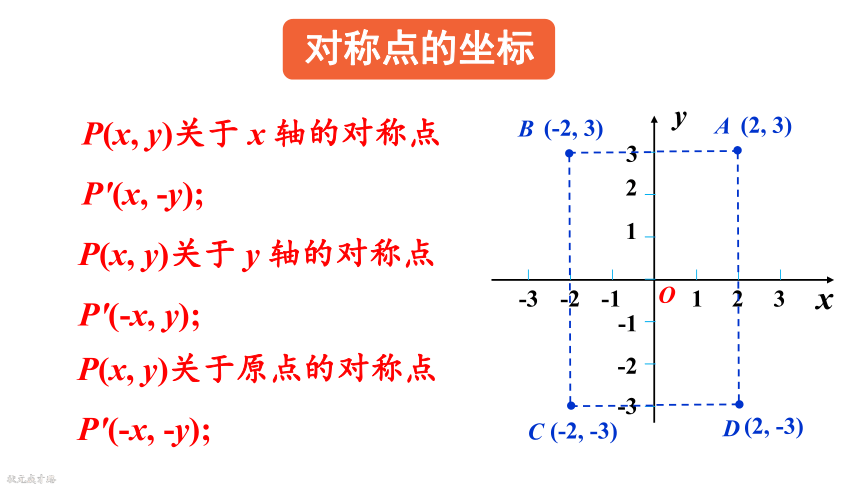
对称点的坐标
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
(2, 3)
A
(-2, 3)
B
(-2, -3)
C
(2, -3)
D
P(x, y)关于 x 轴的对称点P′(x, -y);
P(x, y)关于 y 轴的对称点P′(-x, y);
P(x, y)关于原点的对称点P′(-x, -y);
4.函数的图象
函数的图象是由直角坐标系中的一系列点组成,图象上的每一点坐标(x,y)代表了函数的一对对应值,即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出相应的点,这些点组成的图形,就是这个函数的图象.
函数图象的画法
第一步:列表(表中给出一些自变量的值以及对应的函数值);
第二步:描点(在直角坐标系中,以自变量为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点);
第三步:连线(按照横坐标由小到大的顺序把所描的各点用平滑的曲线连接起来);
一次函数通常可以表示为 y = kx + b 的形式,其中 k、b 是常数,k ≠ 0.
特别地,当 b = 0 时,一次函数 y = kx(常数 k ≠ 0)也叫做正比例函数.
5.一次函数
6.反比例函数
一般地,形如 (k 为常数,k ≠ 0)的函数,叫做反比例函数,其中 x 是自变量,y 是函数.
自变量 x 的取值范围是不等于 0 的一切实数.
函数 一次函数 反比例函数
解析式 y=kx+b(k≠0)
图像形状 直线 双曲线
k>0 位置 一、三象限 一、三象限
增减性 从左到右上升
y随x的增大而增大 从左到右下降
y随x的增大而减小
k<0 位置 二、四象限 二、四象限
增减性 从左到右下降
y随x的增大而减小 从左到右上升
y随x的增大而增大
7.一次函数与一元一次方程(组)的关系
方程kx+b=0(k≠0)的解即为直线y=kx+b(k≠0)与x轴交点的横坐标.
解方程kx+b=0(k≠0),相当于一次函数y=kx+b(k≠0)的函数值为0时,求自变量的值.
两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而两个一次函数的关系式就是方程组中的两个方程,所以交点的坐标就是方程组的解.据此,我们可以利用图象来求某些方程组的解.
例如,图中的两条直线:y=2x-5和y=-x+1,它们的交点坐标(2,-1)就是方程组 的解
y=2x-5
y=-x+1
x
y
O
1
2
3
4
1
2
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
8.一次函数与一元一次不等式的关系
解一元一次不等式kx+b>0(k≠0),相当于一次函数y=kx+b的函数值大于0时,求自变量的取值范围.即图像位于x轴上方部分的x的取值范围.
解一元一次不等式kx+b<0(k≠0),相当于一次函数y=kx+b的函数值小于0时,求自变量的取值范围.即图像位于x轴下方部分的x的取值范围.
随堂练习
1. 已知函数y=y1+y2,且y1与x成反比例函数关系,y2与(x-2)成正比例函数关系.当x=1时,y=-1;当x=3时,y=5.求:x=5时,y的值.
分析:应先用待定系数法写出函数的解析式.
解:由已知,y1= (k1≠0,k1是常数),又由已知y2=k2(x-2)(k2≠0,k2是常数),所以y= +k2(x-2).①
由已知,当x=1时,y=-1,代入①,得-1=k1+k2(-1),即k1-k2=-1.②
由已知,当x=3时,y=5,代入①,得5= +k2,即k1+3k2=15.③
得
所求的函数解析式是y= +4(x-2).
当x=5时,y= +4×(5-2)=12.6.
2.转炉炼钢产生的棕红色烟尘会污染大气,某装置可通过回收棕红色烟尘中的氧化铁从而降低污染.该装置的氧化铁回收率与其通过的电流有关,现经过试验得到下列数据:
如图建立直角坐标系,用横坐标表示通过的电流强度,纵坐标表示氧化铁回收率.
(1)将试验所得数据在上图所给的直角坐标系中用点表示(注:该图中坐标轴的交点代表点(1,70));
(2)用线段将题(1)所画的点从左到右顺次连接,若此图象来模拟氧化铁回收率y关于通过电流x的函数关系式,试写出该函数在1.7≤x≤2.4时的表达式;
(3)利用题(2)所得的关系,求氧化铁回收率大于85%时,该装置通过是电流应该控制的范围(精确到0.1A).
解:(1)如下图;
(2)将题(1)所画的点从左到右顺次连接,如下图;
(3)当1.7≤x<1.9时,由45x+2.5>85,得1.8<x<1.9;
当2.1≤x<2.4时,由-30x+150>85,得2.1≤x<2.2;
又当1.9≤x<2.1时,恒有-5x+97.5>85.
综上可知:满足要求时,该装置的电流应控制在1.8A至2.2A之间.
3.如图,已知一次函数y=kx+b的图象与反比例函数y= 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
解:(1)xA=-2代入y= 中,得yA=4.
所以点A的坐标是(-2,4).
把yB=-2代入y= 中,得xB=4.
所以点B的坐标是(4,-2).
把A、B的坐标代入y=kx+b中,得 解得
所以一次函数的解析式是y=-x+2.
(2)当y=0时,0=-x+2,得x=2,
所以M(2,0),即OM=2.
S△AOB=S△AOM+S△BOM
= ×2×4+ ×2×2
=6.
课堂小结
谈谈你在这节课中,有什么收获?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
章末复习
华东师大·八年级数学下册
知识结构
知识回顾
1.函数的概念
变量:变化过程中可以取不同数值的量.
常量:变化过程中保持不变的量.
函数:如果在一个变化过程中,有两个变量x和y,对于每一个x值,y都有惟一的值和它对应,我们就说x是自变量,y是因变量,y是x的函数.
2.如何求函数的自变量取值范围
考虑两个方面,其一是分母不等于0,其二是开偶次方的被开方数为非负数,对于实际问题,应根据具体情况而定.
3.关于平面直角坐标系
平面上的点与有序实数对成一一对应关系,其含义是坐标平面上的每一个点都可以用一对有序实数来表示,反过来,每一对有序实数都可以在坐标平面上描出一点,这样数与形就有机地结合在一起.我们可以在平面上建立直角坐标系定出点的位置.
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
A
F
D
C
B
E
+
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x 轴
y 轴
+
-
+
-
-
+
-
x
0
0
y
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不属于任何一个象限.
对称点的坐标
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
(2, 3)
A
(-2, 3)
B
(-2, -3)
C
(2, -3)
D
P(x, y)关于 x 轴的对称点P′(x, -y);
P(x, y)关于 y 轴的对称点P′(-x, y);
P(x, y)关于原点的对称点P′(-x, -y);
4.函数的图象
函数的图象是由直角坐标系中的一系列点组成,图象上的每一点坐标(x,y)代表了函数的一对对应值,即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出相应的点,这些点组成的图形,就是这个函数的图象.
函数图象的画法
第一步:列表(表中给出一些自变量的值以及对应的函数值);
第二步:描点(在直角坐标系中,以自变量为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点);
第三步:连线(按照横坐标由小到大的顺序把所描的各点用平滑的曲线连接起来);
一次函数通常可以表示为 y = kx + b 的形式,其中 k、b 是常数,k ≠ 0.
特别地,当 b = 0 时,一次函数 y = kx(常数 k ≠ 0)也叫做正比例函数.
5.一次函数
6.反比例函数
一般地,形如 (k 为常数,k ≠ 0)的函数,叫做反比例函数,其中 x 是自变量,y 是函数.
自变量 x 的取值范围是不等于 0 的一切实数.
函数 一次函数 反比例函数
解析式 y=kx+b(k≠0)
图像形状 直线 双曲线
k>0 位置 一、三象限 一、三象限
增减性 从左到右上升
y随x的增大而增大 从左到右下降
y随x的增大而减小
k<0 位置 二、四象限 二、四象限
增减性 从左到右下降
y随x的增大而减小 从左到右上升
y随x的增大而增大
7.一次函数与一元一次方程(组)的关系
方程kx+b=0(k≠0)的解即为直线y=kx+b(k≠0)与x轴交点的横坐标.
解方程kx+b=0(k≠0),相当于一次函数y=kx+b(k≠0)的函数值为0时,求自变量的值.
两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而两个一次函数的关系式就是方程组中的两个方程,所以交点的坐标就是方程组的解.据此,我们可以利用图象来求某些方程组的解.
例如,图中的两条直线:y=2x-5和y=-x+1,它们的交点坐标(2,-1)就是方程组 的解
y=2x-5
y=-x+1
x
y
O
1
2
3
4
1
2
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
8.一次函数与一元一次不等式的关系
解一元一次不等式kx+b>0(k≠0),相当于一次函数y=kx+b的函数值大于0时,求自变量的取值范围.即图像位于x轴上方部分的x的取值范围.
解一元一次不等式kx+b<0(k≠0),相当于一次函数y=kx+b的函数值小于0时,求自变量的取值范围.即图像位于x轴下方部分的x的取值范围.
随堂练习
1. 已知函数y=y1+y2,且y1与x成反比例函数关系,y2与(x-2)成正比例函数关系.当x=1时,y=-1;当x=3时,y=5.求:x=5时,y的值.
分析:应先用待定系数法写出函数的解析式.
解:由已知,y1= (k1≠0,k1是常数),又由已知y2=k2(x-2)(k2≠0,k2是常数),所以y= +k2(x-2).①
由已知,当x=1时,y=-1,代入①,得-1=k1+k2(-1),即k1-k2=-1.②
由已知,当x=3时,y=5,代入①,得5= +k2,即k1+3k2=15.③
得
所求的函数解析式是y= +4(x-2).
当x=5时,y= +4×(5-2)=12.6.
2.转炉炼钢产生的棕红色烟尘会污染大气,某装置可通过回收棕红色烟尘中的氧化铁从而降低污染.该装置的氧化铁回收率与其通过的电流有关,现经过试验得到下列数据:
如图建立直角坐标系,用横坐标表示通过的电流强度,纵坐标表示氧化铁回收率.
(1)将试验所得数据在上图所给的直角坐标系中用点表示(注:该图中坐标轴的交点代表点(1,70));
(2)用线段将题(1)所画的点从左到右顺次连接,若此图象来模拟氧化铁回收率y关于通过电流x的函数关系式,试写出该函数在1.7≤x≤2.4时的表达式;
(3)利用题(2)所得的关系,求氧化铁回收率大于85%时,该装置通过是电流应该控制的范围(精确到0.1A).
解:(1)如下图;
(2)将题(1)所画的点从左到右顺次连接,如下图;
(3)当1.7≤x<1.9时,由45x+2.5>85,得1.8<x<1.9;
当2.1≤x<2.4时,由-30x+150>85,得2.1≤x<2.2;
又当1.9≤x<2.1时,恒有-5x+97.5>85.
综上可知:满足要求时,该装置的电流应控制在1.8A至2.2A之间.
3.如图,已知一次函数y=kx+b的图象与反比例函数y= 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
解:(1)xA=-2代入y= 中,得yA=4.
所以点A的坐标是(-2,4).
把yB=-2代入y= 中,得xB=4.
所以点B的坐标是(4,-2).
把A、B的坐标代入y=kx+b中,得 解得
所以一次函数的解析式是y=-x+2.
(2)当y=0时,0=-x+2,得x=2,
所以M(2,0),即OM=2.
S△AOB=S△AOM+S△BOM
= ×2×4+ ×2×2
=6.
课堂小结
谈谈你在这节课中,有什么收获?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
