2022-2023学年华东师大版八年级数学下册第十七章 函数 校本作业(16课时 无答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学下册第十七章 函数 校本作业(16课时 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 776.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 14:57:26 | ||
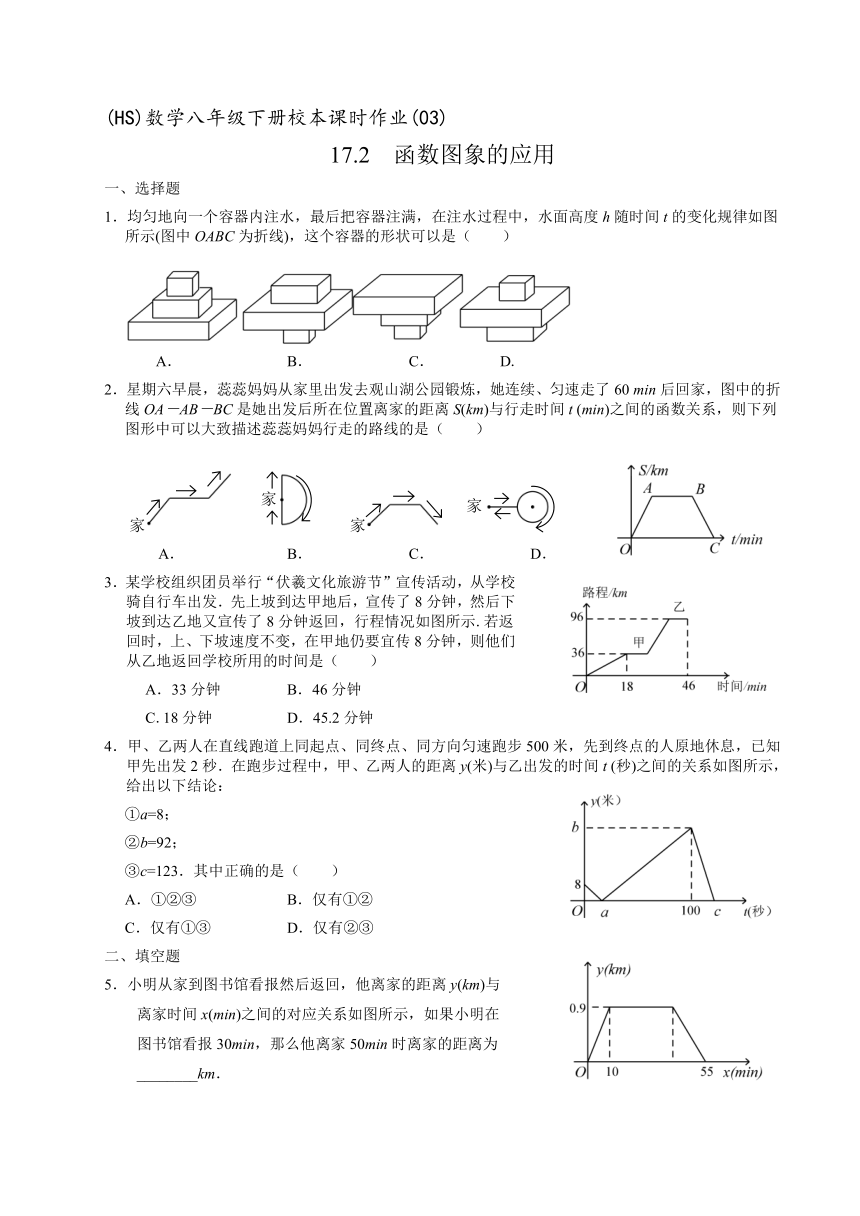
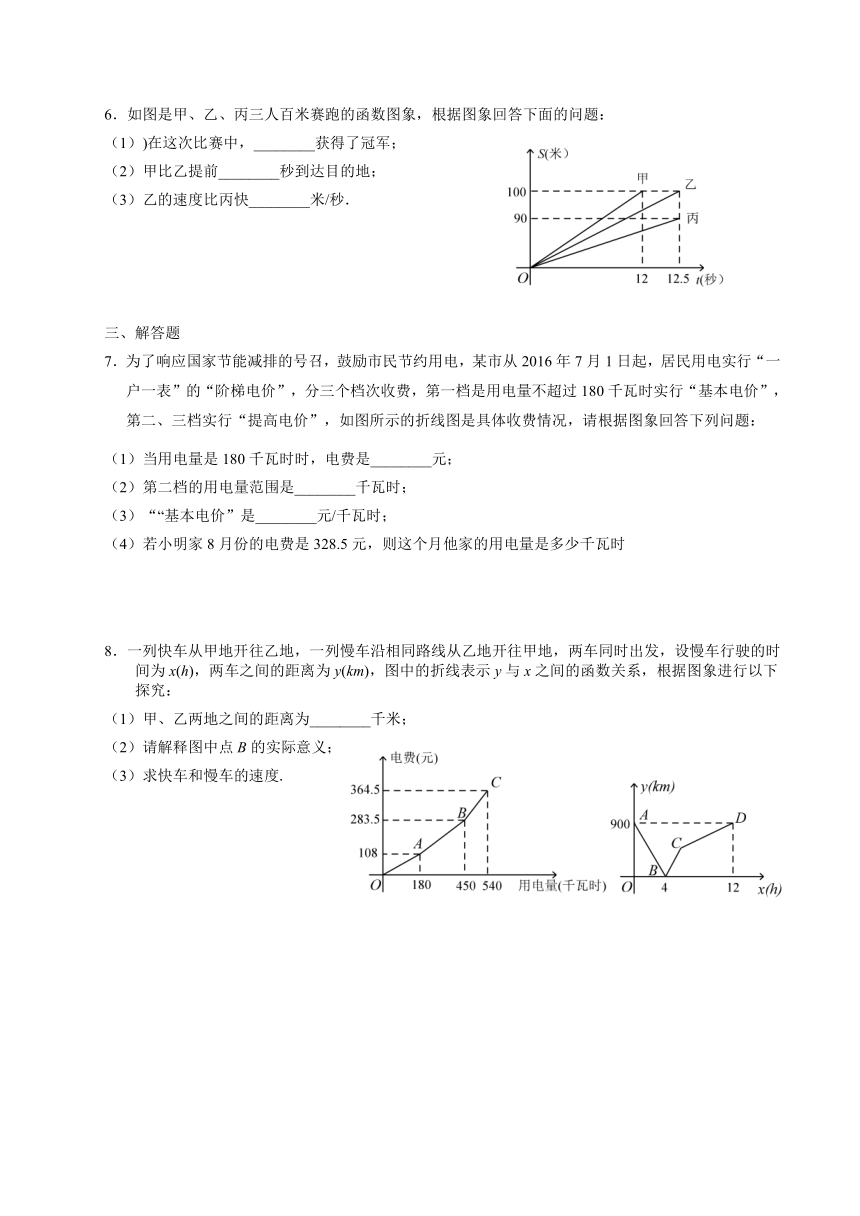
图片预览