第六章 平面向量及其应用-高一年级数学人教版(2019)必修二单元练习(含解析)
文档属性
| 名称 | 第六章 平面向量及其应用-高一年级数学人教版(2019)必修二单元练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 21:21:04 | ||
图片预览




文档简介
平面向量及其应用
1. 已知向量,,则向量与夹角的大小为( )
A. B. C. D.
2. 已知向量,,若与共线,则m的值为( )
A. B. 2 C. D.
3. 在中,,,,AD为BC边上的高,O为AD上靠近点A的三等分点,且,其中,,则( )
A. B. C. D.
4. 已知的三个内角A、B、C所对边分别为a、b、c,则“”是“为直角三角形”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 如图,已知正六边形,下列向量的数量积中最大的是( )
A. B. C. D.
6. 为测量两塔塔尖之间的距离,某数学建模活动小组构建了如图所示的几何模型.若平面ABC,平面ABC,,,,,,则塔尖MN之间的距离为( )
A. B. C. 150m D.
7. 已知平面向量,,,,若对任意的正实数,的最小值为,则此时( )
A. 1 B. 2 C. D.
8. 中,角A,B,C的对边分别为a,b,c,已知,,则的最大值为( )
A. B. C. D.
9. 已知是边长为2的等边三角形,若向量,满足,,则( )
A. B. C. D.
10. 已知向量,,,,则下列说法正确的是( )
A. 若,则有最小值
B. 若,则有最小值
C. 若,则的值为
D. 若,则的值为1
11. 对于,有如下判断,其中正确的判断是( )
A. 在非等腰中,满足,则为钝角三角形;
B. 若,,,则符合条件的有两个;
C. 若,则为锐角三角形;
D. 若的面积,,则的最大值为
12. 重庆荣昌折扇是中国四大名扇之一,始于1551年明代嘉靖年间,明末已成为贡品人朝,产品以其精湛的工业制作而闻名于海内外.经历代艺人刻苦钻研、精工创制,荣昌折扇逐步发展成为具有独特风格的中国传统工艺品,其精雅宜士人,其华灿宜艳女,深受各阶层人民喜爱.古人曾有诗赞曰:“开合清风纸半张,随机舒卷岂寻常;金环并束龙腰细,玉栅齐编凤翅长,偏称游人携袖里,不劳侍女执花傍;宫罗旧赐休相妒,还汝团圆共夜凉”图1为荣昌折扇,其平面图为图2的扇形COD,其中,,动点P在上含端点,连结OP交扇形OAB的弧于点Q,且,则下列说法正确的是( )
A. 若,则 B. 若,则
C. D.
13. 已知向量,为单位向量,若与的夹角为,则__________.
14. 如图,在中,,P是BN上的一点,若,则实数m的值为__________.
15. 在中,内角的对边分别为,,且,则外接圆的面积为__________.
16. 在边长为1的等边三角形ABC中,D为线段BC上的动点,且交AB于点E,且交AC于点F,则的值为__________;的最小值为__________ .
17. 已知向量与的夹角,且,
求,
求与的夹角的余弦值.
18. 在锐角中,内角A、B、C所对的边分别为a,b,c,,,向量,的夹角为
求角
若,求周长的取值范围.
19. 如图,在边长为4的正中,E为AB的中点,D为BC中点,,令,,
试用、表示向量;
延长线段EF交AC于P,求的值.
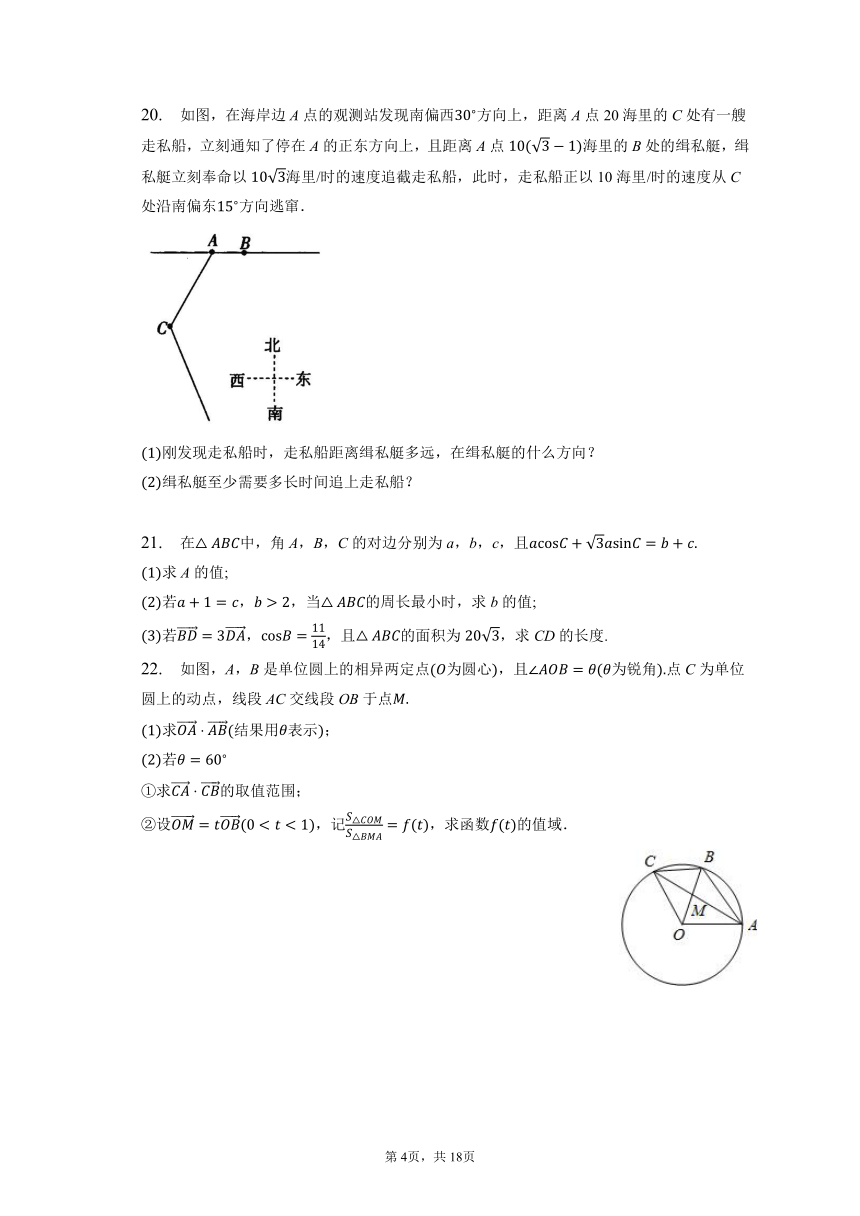
20. 如图,在海岸边A点的观测站发现南偏西方向上,距离A点20海里的C处有一艘走私船,立刻通知了停在A的正东方向上,且距离A点海里的B处的缉私艇,缉私艇立刻奉命以海里/时的速度追截走私船,此时,走私船正以10海里/时的速度从C处沿南偏东方向逃窜.
刚发现走私船时,走私船距离缉私艇多远,在缉私艇的什么方向?
缉私艇至少需要多长时间追上走私船?
21. 在中,角A,B,C的对边分别为a,b,c,且
求A的值;
若,,当的周长最小时,求b的值;
若,,且的面积为,求CD的长度.
22. 如图,A,B是单位圆上的相异两定点为圆心,且为锐角点C为单位圆上的动点,线段AC交线段OB于点
求结果用表示;
若
①求的取值范围;
②设,记,求函数的值域.
答案和解析
1.D
【解析】
【分析】
本题考查利用向量数量积的坐标运算求向量的夹角,属于基础题.
利用向量数量积的坐标运算即可求解.
【解答】
解:因为,,
所以,
又因为 ,
所以
故选:
2.D
【解析】
【分析】
本题考查平面向量共线的概念及充要条件,平面向量坐标的运算,属于基础题.由向量的数乘及坐标加减法运算求得与的坐标,代入向量共线的坐标表示即可求解m的值.
【解答】解:,,
则,
,
又与平行,
,
解得:
故选
3.C
【解析】
【分析】
本题考查平面向量的基本定理和线性运算,属于基础题.
利用平面向量的线性运算求得,求出,,即可得解.
【解答】
解:在中,,所以,
所以
所以,
故选
4.A
【解析】
【分析】
本题考查了正弦定理、诱导公式、两角和的正弦公式的简单运用,充分条件、必要条件的判断,属于中档题.
由已知结合正弦定理可得,利用三角形的内角和及和角的正弦公式化简可得A为直角,结合充分条件及必要条件进行判断即可.
【解答】
解:因为,
由正弦定理可得,即,
所以,
所以,
因为,所以,,
则,为直角三角形,
但为直角三角形时不一定是,
所以是为直角三角形的充分不必要条件.
故选:
5.A
【解析】
【分析】
本题主要考查平面向量的数量积运算.注意向量数量积的定义和运算法则,属于基础题.
设边长,利用正六边形的性质求相应的长度和夹角,再根据向量数量积的定义,从而得到答案.
【解答】
解:已知正六边形,设边长,
则,,
故;
由,,
可得,
由,,,
可得,,
综上所述,数量积中最大的是
故选:
6.B
【解析】
【分析】
本题考查解三角形,数形结合思想,考查学生的计算能力,属于中档题.
通过所给条件依次求出MC,NC,再由余弦定理可求得
【解答】
解:由题得,在中,,则,
在中,,
则在中,由余弦定理可得 ,
则
故选:
7.D
【解析】
【分析】
本题考查了向量的坐标运算,向量的模以及三角恒等变换,计算时需要注意对取值进行讨论,得到取到最小值的条件,然后求解.属于较难题.
对任意的正实数,的最小值为,将表示为含有,,的算式,配方讨论得到,关系后,得到的值,即可求得
【解答】
解:
若,
则当时有最小值,
而,故不成立.
当时有最小值,
,另一解为负,舍去,
故答案选:
8.D
【解析】
【分析】
本题考查了正弦定理、余弦定理的应用,三角形的面积公式,以及利用基本不等式求最值问题,考查化简、变形能力,属于较难题.
由正弦定理和条件得,由余弦定理及基本不等式得到,根据面积公式求出面积的最大值.
【解答】
解:,
,又,
则,,
由余弦定理及,
得,
,
又,得,当且仅当时取等号,
的面积
当时,的面积S有最大值,
故选
9.AC
【解析】
【分析】
本题考查平面向量的线性运算,考查分析与计算能力,属于基础题.
根据向量加法的三角形法则判断A,根据数量积的定义判断B,根据数量积的运算律判断C、D;
【解答】
解:因为,,
对于A:,故A正确;
对于B:,故B错误;
对于C:,则,故C正确:
对于D:,即,故D错误;
故选:
10.AB
【解析】
【分析】
本题考查向量垂直和向量平行的坐标运算,向量的数量积的坐标运算,考查利用基本不等式求解最值问题,属于中档题.
根据向量的坐标运算,求得,结合向量平行和垂直的坐标运算以及基本不等式,对每个选项进行逐一分析,即可判断和选择.
【解答】
解:,,
对A:若,,则,
当且仅当,即,时取得等号,故选项A正确;
对B:若,,则,
当且仅当,时取得等号,故选项B正确;
对C:若,则,即,,,当且仅当时取得等号,
则,故选项C错误;
对D:,则,又因为,
所以这样的a,b不存在,故选项D错误.
故选
11.ABD
【解析】
【分析】
本题重点考查解三角形和三角恒等变换,涉及三角函数的性质,属于中档题.
利用正弦函数的性质可判断A,由正弦定理可判断B,由特殊值法可判断C,利用正、余弦定理,结合正切函数的性质可判断
【解答】
解:对于A、由题意,因为,
则或,
则舍或,
则,则为钝角三角形,故A正确;
对于B、由题意得,
又,则符合条件的有两个,故B正确;
对于C、取,,
则,但此时为直角三角形,故C错误;
对于D、因为,
则,
故,
又A为的内角,则,
则,故D正确.
故选:
12.ABD
【解析】
【分析】
本题考查了三角函数与向量的综合.
建立平面直角坐标系,表示出相关点的坐标,设,可得,由,结合题中条件可判断A,B;表示出相关向量的坐标,利用数量积的运算律,结合三角函数的性质,可判断C,
【解答】
解:如图,作,分别以OC,OE为x,y轴建立平面直角坐标系,
则,
设,则,
由可得,且,,
若,则,
解得,负值舍去,故,A正确;
若,则,故B正确;
由于,故,故,故C错误;
由于,
故,
而,
故,故D正确,
故选
13.1
【解析】
【分析】
本题考查单位向量的基本概念以及两个向量减法运算后模的求法,属于基础题.
算出两个向量减法运算后模的平方的值,就能算出结果.
【解答】
解:由题意可知,
故答案为:
14.
【解析】
【分析】
本题主要考查平面向量的线性运算、共线定理,平面向量基本定理的运用,属于中档题.
解法1:先根据得到,从而可得,再根据三点共线定理,即可得到m的值.
解法2:根据图形和向量的转化用去表示,根据图形可得:,设,通过向量线性运算可得:,从而根据平面向量基本定理列方程组,解方程组得m的值.
【解答】
解法1:因为,所以,
又,
所以
因为点三点共线,
所以,
解得:
解法2:
因为,设,
所以,
因为,所以,
又,
所以,
所以,
又,
所以 解得: ,
所以
故答案为
15.
【解析】
【分析】
本题考查了正弦定理和二倍角公式及其应用 ,属于中档题.
由正弦定理及二倍角公式可求得角A的余弦值,进而求得角A的正弦值以及外接圆半径,故可得解.
【解答】
解:在中,由正弦定理得,则,
,,
,
因为,
,
设外接圆的半径为R,
由正弦定理得,,
故外接圆的面积为
故答案为
16.1
【解析】
【分析】
本题考查向量的数量积的定义,向量的运算法则,二次函数求最值,属于中档题.
设,表示出,,,利用数量积的定义与性质,分别表示出与即可求出.
【解答】
解:如图,设,
是边长为1等边三角形,,
,,,,
,
是边长为等边三角形,,
,
则,
,,
的最小值为
故答案为:1,
17.解:由已知,得
设与的夹角为
则,
与的夹角的余弦值为
【解析】本题考查向量的数量积,向量的模和向量的夹角,考查了计算能力,属于基础题.
根据向量的数量积进行求解即可;再利用向量的模的公式,根据,代入求解即可;
设与的夹角为,然后根据,将数值代入即可得到答案.
18.解:由,,有
由,可得,有;
由和正弦定理可知,
可得,
又由为锐角三角形,可得
由,有,可得,有
故周长的取值范围为
【解析】本题考查解三角形的综合运用,属于中档题.
19.解:
;
令,,
,
,
,解得:,
,,
【解析】本题考查了向量的加减与数乘混合运算和向量的数量积,属于中档题.
由向量加法和减法的三角形法则可得结果;
令,,由和,可得x、y的值,再由向量的数量积计算可得.
20.解:由题意可知,,
在中,由余弦定理得
由正弦定理得,解得,所以
故刚发现走私船时,走私船距缉私艇海里,在缉私艇的南偏西方向上.
如图,设t小时后缉私艇在D处追上走私船,则,
在中,由正弦定理得
解得,则,所以是等腰三角形
,即
故缉私艇至少需要小时追上走私船.
【解析】本题考查解三角形的实际应用,属于中档题.
利用余弦定理求BC,利用正弦定理求即可;
利用正弦定理判断出是等腰三角形,即可求出所需的最少时间.
21.解:由及正弦定理,
得,
因为,且,
所以,即,
因为,所以
由余弦定理,得,
将代入,整理,得,
因为,所以的周长为,
当且仅当,即时取等号,
所以当的周长最小时,
由的面积为,得,
所以①,
又,所以,,
由正弦定理,得②,
由①②可得,,
因为,所以,
在中,由余弦定理,得,
所以
【解析】 本题重点考查正弦定理与余弦定理解三角形,基本不等式的应用,简单的三角变换,考查逻辑推理,转化与化归及运算能力,属稍难题.
利用正弦定理,两角和的正弦公式及辅助角公式化简求解即可.
利用余弦定理及基本不等式即可,注意取等号时的条件.
利用正余弦定理及三角形的面积公式等计算即可求解.
22.解:;
当时,
①
设,由条件知,,
,,
;
②设,则,
,
由可得,,
即,整理得,
,
即
而
令,
当时,;
当时,,利用单调性定义可证明函数在和都是递减的,
设,且,则
则,故,所以在上单调递减,
由于是奇函数,则在和单调递减,
因此,或,
函数值域是
【解析】本题考查平面向量的数量积运算,考查了三角函数值域的求法,训练了利用配方法和函数单调性求函数的值域,考查学生的逻辑思维能力和运算能力,属于困难题.
直接利用平面向量的数量积把用表示;
①利用向量的数量积运算结合向量的加减法运算把用表示,化简整理后由得范围求得的取值范围;
②设,则,,由可得,,整理得,然后把转化为含有t的代数式,换元后借助于函数单调性求得函数的值域.
第4页,共19页
1. 已知向量,,则向量与夹角的大小为( )
A. B. C. D.
2. 已知向量,,若与共线,则m的值为( )
A. B. 2 C. D.
3. 在中,,,,AD为BC边上的高,O为AD上靠近点A的三等分点,且,其中,,则( )
A. B. C. D.
4. 已知的三个内角A、B、C所对边分别为a、b、c,则“”是“为直角三角形”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 如图,已知正六边形,下列向量的数量积中最大的是( )
A. B. C. D.
6. 为测量两塔塔尖之间的距离,某数学建模活动小组构建了如图所示的几何模型.若平面ABC,平面ABC,,,,,,则塔尖MN之间的距离为( )
A. B. C. 150m D.
7. 已知平面向量,,,,若对任意的正实数,的最小值为,则此时( )
A. 1 B. 2 C. D.
8. 中,角A,B,C的对边分别为a,b,c,已知,,则的最大值为( )
A. B. C. D.
9. 已知是边长为2的等边三角形,若向量,满足,,则( )
A. B. C. D.
10. 已知向量,,,,则下列说法正确的是( )
A. 若,则有最小值
B. 若,则有最小值
C. 若,则的值为
D. 若,则的值为1
11. 对于,有如下判断,其中正确的判断是( )
A. 在非等腰中,满足,则为钝角三角形;
B. 若,,,则符合条件的有两个;
C. 若,则为锐角三角形;
D. 若的面积,,则的最大值为
12. 重庆荣昌折扇是中国四大名扇之一,始于1551年明代嘉靖年间,明末已成为贡品人朝,产品以其精湛的工业制作而闻名于海内外.经历代艺人刻苦钻研、精工创制,荣昌折扇逐步发展成为具有独特风格的中国传统工艺品,其精雅宜士人,其华灿宜艳女,深受各阶层人民喜爱.古人曾有诗赞曰:“开合清风纸半张,随机舒卷岂寻常;金环并束龙腰细,玉栅齐编凤翅长,偏称游人携袖里,不劳侍女执花傍;宫罗旧赐休相妒,还汝团圆共夜凉”图1为荣昌折扇,其平面图为图2的扇形COD,其中,,动点P在上含端点,连结OP交扇形OAB的弧于点Q,且,则下列说法正确的是( )
A. 若,则 B. 若,则
C. D.
13. 已知向量,为单位向量,若与的夹角为,则__________.
14. 如图,在中,,P是BN上的一点,若,则实数m的值为__________.
15. 在中,内角的对边分别为,,且,则外接圆的面积为__________.
16. 在边长为1的等边三角形ABC中,D为线段BC上的动点,且交AB于点E,且交AC于点F,则的值为__________;的最小值为__________ .
17. 已知向量与的夹角,且,
求,
求与的夹角的余弦值.
18. 在锐角中,内角A、B、C所对的边分别为a,b,c,,,向量,的夹角为
求角
若,求周长的取值范围.
19. 如图,在边长为4的正中,E为AB的中点,D为BC中点,,令,,
试用、表示向量;
延长线段EF交AC于P,求的值.
20. 如图,在海岸边A点的观测站发现南偏西方向上,距离A点20海里的C处有一艘走私船,立刻通知了停在A的正东方向上,且距离A点海里的B处的缉私艇,缉私艇立刻奉命以海里/时的速度追截走私船,此时,走私船正以10海里/时的速度从C处沿南偏东方向逃窜.
刚发现走私船时,走私船距离缉私艇多远,在缉私艇的什么方向?
缉私艇至少需要多长时间追上走私船?
21. 在中,角A,B,C的对边分别为a,b,c,且
求A的值;
若,,当的周长最小时,求b的值;
若,,且的面积为,求CD的长度.
22. 如图,A,B是单位圆上的相异两定点为圆心,且为锐角点C为单位圆上的动点,线段AC交线段OB于点
求结果用表示;
若
①求的取值范围;
②设,记,求函数的值域.
答案和解析
1.D
【解析】
【分析】
本题考查利用向量数量积的坐标运算求向量的夹角,属于基础题.
利用向量数量积的坐标运算即可求解.
【解答】
解:因为,,
所以,
又因为 ,
所以
故选:
2.D
【解析】
【分析】
本题考查平面向量共线的概念及充要条件,平面向量坐标的运算,属于基础题.由向量的数乘及坐标加减法运算求得与的坐标,代入向量共线的坐标表示即可求解m的值.
【解答】解:,,
则,
,
又与平行,
,
解得:
故选
3.C
【解析】
【分析】
本题考查平面向量的基本定理和线性运算,属于基础题.
利用平面向量的线性运算求得,求出,,即可得解.
【解答】
解:在中,,所以,
所以
所以,
故选
4.A
【解析】
【分析】
本题考查了正弦定理、诱导公式、两角和的正弦公式的简单运用,充分条件、必要条件的判断,属于中档题.
由已知结合正弦定理可得,利用三角形的内角和及和角的正弦公式化简可得A为直角,结合充分条件及必要条件进行判断即可.
【解答】
解:因为,
由正弦定理可得,即,
所以,
所以,
因为,所以,,
则,为直角三角形,
但为直角三角形时不一定是,
所以是为直角三角形的充分不必要条件.
故选:
5.A
【解析】
【分析】
本题主要考查平面向量的数量积运算.注意向量数量积的定义和运算法则,属于基础题.
设边长,利用正六边形的性质求相应的长度和夹角,再根据向量数量积的定义,从而得到答案.
【解答】
解:已知正六边形,设边长,
则,,
故;
由,,
可得,
由,,,
可得,,
综上所述,数量积中最大的是
故选:
6.B
【解析】
【分析】
本题考查解三角形,数形结合思想,考查学生的计算能力,属于中档题.
通过所给条件依次求出MC,NC,再由余弦定理可求得
【解答】
解:由题得,在中,,则,
在中,,
则在中,由余弦定理可得 ,
则
故选:
7.D
【解析】
【分析】
本题考查了向量的坐标运算,向量的模以及三角恒等变换,计算时需要注意对取值进行讨论,得到取到最小值的条件,然后求解.属于较难题.
对任意的正实数,的最小值为,将表示为含有,,的算式,配方讨论得到,关系后,得到的值,即可求得
【解答】
解:
若,
则当时有最小值,
而,故不成立.
当时有最小值,
,另一解为负,舍去,
故答案选:
8.D
【解析】
【分析】
本题考查了正弦定理、余弦定理的应用,三角形的面积公式,以及利用基本不等式求最值问题,考查化简、变形能力,属于较难题.
由正弦定理和条件得,由余弦定理及基本不等式得到,根据面积公式求出面积的最大值.
【解答】
解:,
,又,
则,,
由余弦定理及,
得,
,
又,得,当且仅当时取等号,
的面积
当时,的面积S有最大值,
故选
9.AC
【解析】
【分析】
本题考查平面向量的线性运算,考查分析与计算能力,属于基础题.
根据向量加法的三角形法则判断A,根据数量积的定义判断B,根据数量积的运算律判断C、D;
【解答】
解:因为,,
对于A:,故A正确;
对于B:,故B错误;
对于C:,则,故C正确:
对于D:,即,故D错误;
故选:
10.AB
【解析】
【分析】
本题考查向量垂直和向量平行的坐标运算,向量的数量积的坐标运算,考查利用基本不等式求解最值问题,属于中档题.
根据向量的坐标运算,求得,结合向量平行和垂直的坐标运算以及基本不等式,对每个选项进行逐一分析,即可判断和选择.
【解答】
解:,,
对A:若,,则,
当且仅当,即,时取得等号,故选项A正确;
对B:若,,则,
当且仅当,时取得等号,故选项B正确;
对C:若,则,即,,,当且仅当时取得等号,
则,故选项C错误;
对D:,则,又因为,
所以这样的a,b不存在,故选项D错误.
故选
11.ABD
【解析】
【分析】
本题重点考查解三角形和三角恒等变换,涉及三角函数的性质,属于中档题.
利用正弦函数的性质可判断A,由正弦定理可判断B,由特殊值法可判断C,利用正、余弦定理,结合正切函数的性质可判断
【解答】
解:对于A、由题意,因为,
则或,
则舍或,
则,则为钝角三角形,故A正确;
对于B、由题意得,
又,则符合条件的有两个,故B正确;
对于C、取,,
则,但此时为直角三角形,故C错误;
对于D、因为,
则,
故,
又A为的内角,则,
则,故D正确.
故选:
12.ABD
【解析】
【分析】
本题考查了三角函数与向量的综合.
建立平面直角坐标系,表示出相关点的坐标,设,可得,由,结合题中条件可判断A,B;表示出相关向量的坐标,利用数量积的运算律,结合三角函数的性质,可判断C,
【解答】
解:如图,作,分别以OC,OE为x,y轴建立平面直角坐标系,
则,
设,则,
由可得,且,,
若,则,
解得,负值舍去,故,A正确;
若,则,故B正确;
由于,故,故,故C错误;
由于,
故,
而,
故,故D正确,
故选
13.1
【解析】
【分析】
本题考查单位向量的基本概念以及两个向量减法运算后模的求法,属于基础题.
算出两个向量减法运算后模的平方的值,就能算出结果.
【解答】
解:由题意可知,
故答案为:
14.
【解析】
【分析】
本题主要考查平面向量的线性运算、共线定理,平面向量基本定理的运用,属于中档题.
解法1:先根据得到,从而可得,再根据三点共线定理,即可得到m的值.
解法2:根据图形和向量的转化用去表示,根据图形可得:,设,通过向量线性运算可得:,从而根据平面向量基本定理列方程组,解方程组得m的值.
【解答】
解法1:因为,所以,
又,
所以
因为点三点共线,
所以,
解得:
解法2:
因为,设,
所以,
因为,所以,
又,
所以,
所以,
又,
所以 解得: ,
所以
故答案为
15.
【解析】
【分析】
本题考查了正弦定理和二倍角公式及其应用 ,属于中档题.
由正弦定理及二倍角公式可求得角A的余弦值,进而求得角A的正弦值以及外接圆半径,故可得解.
【解答】
解:在中,由正弦定理得,则,
,,
,
因为,
,
设外接圆的半径为R,
由正弦定理得,,
故外接圆的面积为
故答案为
16.1
【解析】
【分析】
本题考查向量的数量积的定义,向量的运算法则,二次函数求最值,属于中档题.
设,表示出,,,利用数量积的定义与性质,分别表示出与即可求出.
【解答】
解:如图,设,
是边长为1等边三角形,,
,,,,
,
是边长为等边三角形,,
,
则,
,,
的最小值为
故答案为:1,
17.解:由已知,得
设与的夹角为
则,
与的夹角的余弦值为
【解析】本题考查向量的数量积,向量的模和向量的夹角,考查了计算能力,属于基础题.
根据向量的数量积进行求解即可;再利用向量的模的公式,根据,代入求解即可;
设与的夹角为,然后根据,将数值代入即可得到答案.
18.解:由,,有
由,可得,有;
由和正弦定理可知,
可得,
又由为锐角三角形,可得
由,有,可得,有
故周长的取值范围为
【解析】本题考查解三角形的综合运用,属于中档题.
19.解:
;
令,,
,
,
,解得:,
,,
【解析】本题考查了向量的加减与数乘混合运算和向量的数量积,属于中档题.
由向量加法和减法的三角形法则可得结果;
令,,由和,可得x、y的值,再由向量的数量积计算可得.
20.解:由题意可知,,
在中,由余弦定理得
由正弦定理得,解得,所以
故刚发现走私船时,走私船距缉私艇海里,在缉私艇的南偏西方向上.
如图,设t小时后缉私艇在D处追上走私船,则,
在中,由正弦定理得
解得,则,所以是等腰三角形
,即
故缉私艇至少需要小时追上走私船.
【解析】本题考查解三角形的实际应用,属于中档题.
利用余弦定理求BC,利用正弦定理求即可;
利用正弦定理判断出是等腰三角形,即可求出所需的最少时间.
21.解:由及正弦定理,
得,
因为,且,
所以,即,
因为,所以
由余弦定理,得,
将代入,整理,得,
因为,所以的周长为,
当且仅当,即时取等号,
所以当的周长最小时,
由的面积为,得,
所以①,
又,所以,,
由正弦定理,得②,
由①②可得,,
因为,所以,
在中,由余弦定理,得,
所以
【解析】 本题重点考查正弦定理与余弦定理解三角形,基本不等式的应用,简单的三角变换,考查逻辑推理,转化与化归及运算能力,属稍难题.
利用正弦定理,两角和的正弦公式及辅助角公式化简求解即可.
利用余弦定理及基本不等式即可,注意取等号时的条件.
利用正余弦定理及三角形的面积公式等计算即可求解.
22.解:;
当时,
①
设,由条件知,,
,,
;
②设,则,
,
由可得,,
即,整理得,
,
即
而
令,
当时,;
当时,,利用单调性定义可证明函数在和都是递减的,
设,且,则
则,故,所以在上单调递减,
由于是奇函数,则在和单调递减,
因此,或,
函数值域是
【解析】本题考查平面向量的数量积运算,考查了三角函数值域的求法,训练了利用配方法和函数单调性求函数的值域,考查学生的逻辑思维能力和运算能力,属于困难题.
直接利用平面向量的数量积把用表示;
①利用向量的数量积运算结合向量的加减法运算把用表示,化简整理后由得范围求得的取值范围;
②设,则,,由可得,,整理得,然后把转化为含有t的代数式,换元后借助于函数单调性求得函数的值域.
第4页,共19页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
