第一章 三角形的证明单元检测试卷A(含答案)
文档属性
| 名称 | 第一章 三角形的证明单元检测试卷A(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 19:33:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2022-20203年八年级(下)第一章三角形的证明检测试卷A
(时间120分钟,满分120分)
一、(共12小题;每小题3分,共36分)
1. 在 中, 和 的度数如下,能判定 是等腰三角形的是
A. , B. ,
C. , D. ,
2. 如图,在 和 ,,,,则下列结论中正确的是
A. 为 中点 B.
C. D.
3. 满足下列条件的三角形中,不是直角三角形的是
A. 三内角之比为 B. 三边长的平方之比为
C. 三边长之比为 D. 三内角之比为
4. 下列说法中,正确的是
A. 过线段中点的直线,叫做这条线段的垂直平分线
B. 若直线 是线段 的垂直平分线,则 也是 的垂直平分线
C. 线段 的中垂线平分线段
D. 线段 的中垂线有无数条
5. 下列各命题的逆命题成立的是
A. 全等三角形的对应角相等
B. 如果两个数相等,那么它们的绝对值相等
C. 两直线平行,同位角相等
D. 如果两个角都是 ,那么这两个角相等
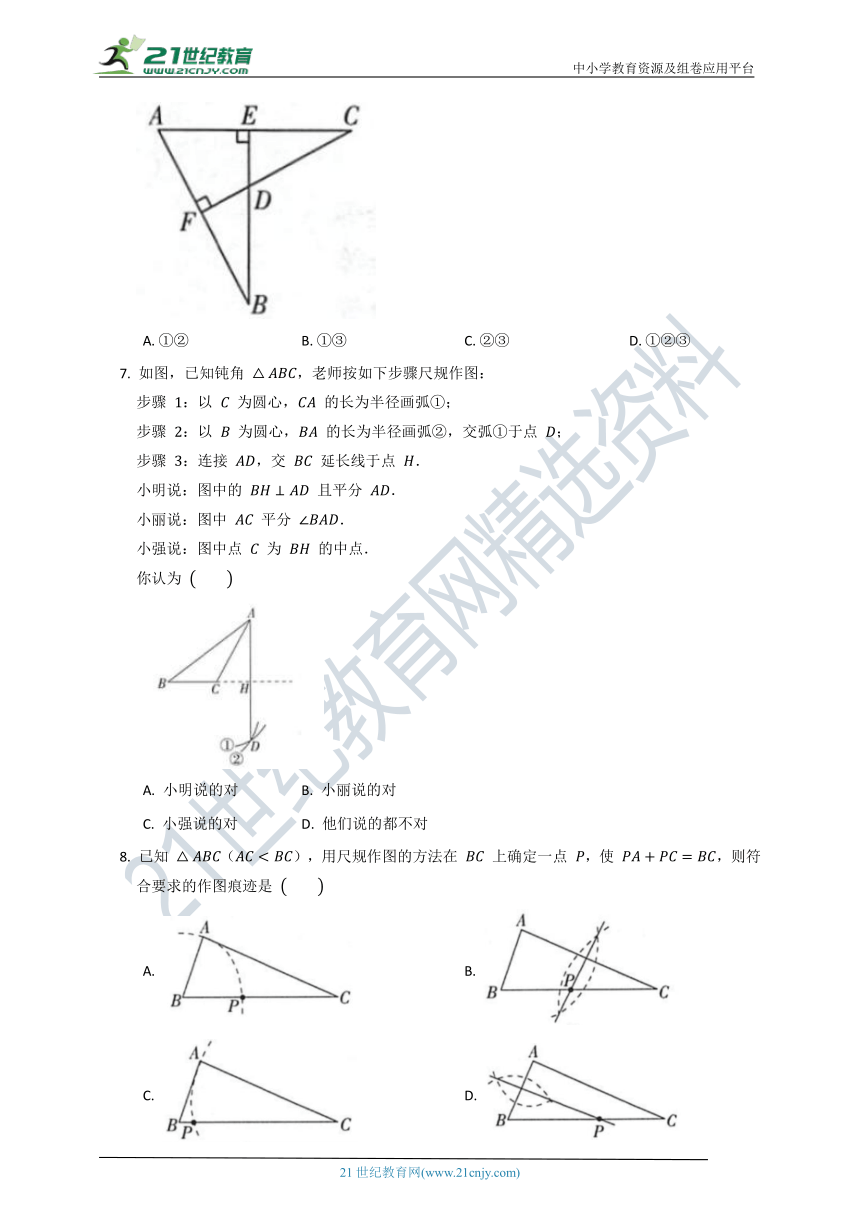
6. 如图, 于点 , 于点 ,, 与 相交于点 ,有以下结论:① ;② ;③点 在 的平分线上.其中正确的是
A. ①② B. ①③ C. ②③ D. ①②③
7. 如图,已知钝角 ,老师按如下步骤尺规作图:
步骤 :以 为圆心, 的长为半径画弧①;
步骤 :以 为圆心, 的长为半径画弧②,交弧①于点 ;
步骤 :连接 ,交 延长线于点 .
小明说:图中的 且平分 .
小丽说:图中 平分 .
小强说:图中点 为 的中点.
你认为
A. 小明说的对 B. 小丽说的对
C. 小强说的对 D. 他们说的都不对
8. 已知 (),用尺规作图的方法在 上确定一点 ,使 ,则符合要求的作图痕迹是
A. B.
C. D.
9. 如图,在 中,,,,垂足为 , 与 关于直线 对称,点 的对称点是点 ,则 的度数为
A. B. C. D.
10. 老师让 个学生猜一猜这次考试中 个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗
A. 甲 B. 乙 C. 丙 D. 丁
11. 如图,在 中,,,, 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是
A. B. C. D.
12. 如图,在 中,,,, 是 的中点,直线 经过点 ,,,垂足分别为 ,,则 的最大值为
A. B. C. D.
二、(共6小题;每小题4分,共24分)
13. 命题“等腰三角形两底角的平分线相等”的逆命题是 .
14. 如图,将两个完全相同的含有 角的三角板拼接在一起,则拼接后的 的形状是 .
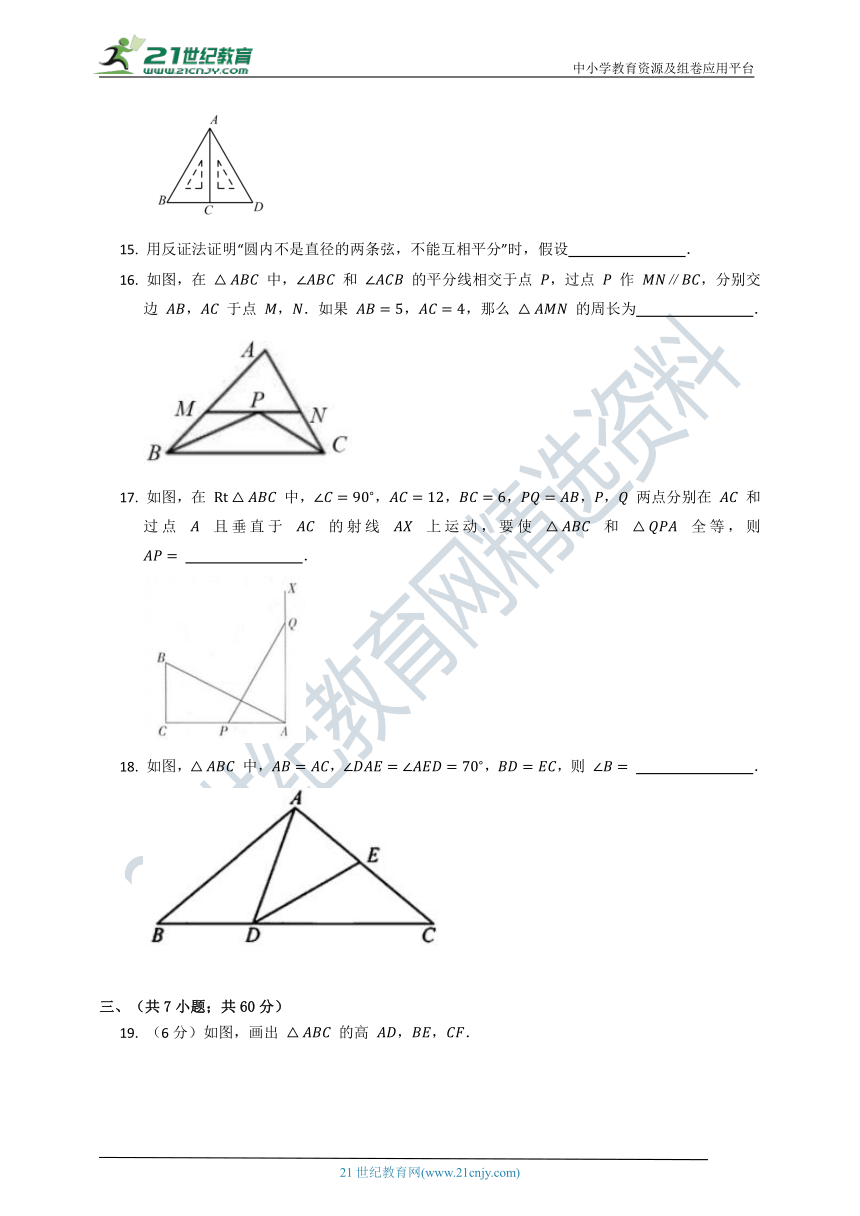
15. 用反证法证明“圆内不是直径的两条弦,不能互相平分”时,假设 .
16. 如图,在 中, 和 的平分线相交于点 ,过点 作 ,分别交边 , 于点 ,.如果 ,,那么 的周长为 .
17. 如图,在 中,,,,,, 两点分别在 和过点 且垂直于 的射线 上运动,要使 和 全等,则 .
18. 如图, 中,,,,则 .
三、(共7小题;共60分)
19. (6分)如图,画出 的高 ,,.
20. (8分)已知 的三边长分别为 ,,.
(1)若 ,, 满足 ,试判断 的形状;
(2)若 ,,且 为整数,求 周长的最大值.
21. (10分)阅读理解
折纸,常常能为证明一个命题提供思路和方法.
例如,在 中,(图 ①),怎样证明 呢
思路:
把 沿 的平分线 翻折,如图 ②,因为 ,所以点 落在 上的点 处.于是,由 ,可得 .
证明:
作 平分 交 于点 ,在 上截取 ,连接 .因为 平分 ,所以 .在 和 中, 所以 ,所以 .因为 ,所以 .
解决问题
在 中,, 为线段 上一点.
(1)如图 ③,当 时,求证:;
(2)如图 ④,当 平分 时,判断 , 和 的数量关系并证明.
22. (8分)【拓展阅读】
无理数的发现
在 多年前,古希腊毕达哥拉斯学派弟子希帕斯发现:以一个正方形的边为长度单位去量这个正方形的对角线,这一对角线的长度不能用有理数表示,从而发现了无理数 ,导致了第一次数学危机.后来,古希腊人终于正视了希帕斯的发现,并进一步给出了证明过程.
阅读材料
假设 是一个有理数,那么可得 ,其中 , 是整数, 与 互素,且 ,则 ,即 , 是 的倍数.再设 ,其中 是整数,则 ,即 , 是 的倍数.那么 与 不互素,与前面假设 与 互素相矛盾.因此 不可能是一个有理数.
【任务】
(1)材料中证明 是无理数的方法是: .
(2)模仿材料中的证明方法,请判断 是否为无理数,并给出理由.
23.(8分) 如图,在气象站台 的正西方向 千米的 处有一台风中心,该台风中心以每小时 千米的速度沿北偏东 的 方向移动,在距离台风中心 千米内的地方都要受到其影响.
(1)台风中心在移动过程中,与气象台 的最短距离是多少
(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长
24. (8分)如图,已知在 中,,, 是 边上的中线, 是 的垂直平分线,交 于点 ,交 于点 .求 的值.
25. (12分)已知 的两个顶点分别为 ,,顶点 在直线 : 上.
(1)若 ,求点 的坐标.
(2) 面积为 ,设点 坐标 ,求 与 函数关系式.
(3)在直线 上是否存在点 ,使得 是直角三角形.若存在,求出点 坐标;若不存在,说明理由.
答案
一
1. B
2. D
3. D
4. C
5. C
6. D
7. A
【解析】如图,连接 ,,
,,
点 ,点 都在线段 的垂直平分线上,
直线 是线段 的垂直平分线,即 且平分 ,
故小明的说法正确;
而 不一定平分 ,故小丽的说法错误;
点 不一定为 的中点,故小强的说法错误.故选A.
8. D
【解析】由选项D的作法知,点 在线段 的垂直平分线上,
,
.
9. A
10. C
【解析】假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好.
11. C
【解析】如图,过点 作 于点 ,交 于点 ,过点 作 于点 ,
是 的平分线,
,这时 有最小值,即 的长度,
,,,
,
,
,
即 的最小值为 .
12. A
【解析】如图,过点 作 于点 ,过点 作 于点 ,
在 中,
,,
,,
在 中,,
,
点 为 中点,
,
在 与 中,
,
,
延长 ,过点 作 于点 ,
可得 ,
在 中,,
当直线 时,最大值为 ,
综上所述, 的最大值为 .
二
13. 有两条角平分线相等的三角形是等腰三角形
14. 等边三角形
15. 圆内不是直径的两条弦,能互相平分
【解析】利用反证法证明时,先假设命题的结论不成立,即本题假设“圆内不是直径的两条弦,能互相平分”.
16.
17. 或
【解析】当 时,.
在 与 ,
;
当点 与点 重合时,,
在 与 中,
.
综上所述,.
18.
三
19. 如图所示:
20. (1) ,
,,
,,
,
为等边三角形.
(2) ,,
,
为整数,
,
周长最大为 ,即周长最大为 .
21. (1) 在 上截取一点 使得 ,连接 ,如图 ① 所示.
,
,
在 和 中,
,
,,
,
,
,
,
,
,
,
.
(2) ,理由如下:
在 上截取一点 使得 ,连接 ,如图 ② 所示,
平分 ,
,
在 和 中,
,
,,
,
,
,
,
,
,
,
.
22. (1) 反证法
(2) 是无理数.
理由:假设 是一个有理数,那么可得 ,其中 , 是整数, 与 互素,且 ,则 ,即 , 是 的倍数.再设 ,其中 是整数,则 ,即 , 是 的倍数.那么 与 不互素,与前面假设 与 互素相矛盾.因此 不可能是一个有理数.
23. (1) 略
(2) 略
24. 略
25. (1)
(2) 当 时,;当 时,.
(3) 存在,,,,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-20203年八年级(下)第一章三角形的证明检测试卷A
(时间120分钟,满分120分)
一、(共12小题;每小题3分,共36分)
1. 在 中, 和 的度数如下,能判定 是等腰三角形的是
A. , B. ,
C. , D. ,
2. 如图,在 和 ,,,,则下列结论中正确的是
A. 为 中点 B.
C. D.
3. 满足下列条件的三角形中,不是直角三角形的是
A. 三内角之比为 B. 三边长的平方之比为
C. 三边长之比为 D. 三内角之比为
4. 下列说法中,正确的是
A. 过线段中点的直线,叫做这条线段的垂直平分线
B. 若直线 是线段 的垂直平分线,则 也是 的垂直平分线
C. 线段 的中垂线平分线段
D. 线段 的中垂线有无数条
5. 下列各命题的逆命题成立的是
A. 全等三角形的对应角相等
B. 如果两个数相等,那么它们的绝对值相等
C. 两直线平行,同位角相等
D. 如果两个角都是 ,那么这两个角相等
6. 如图, 于点 , 于点 ,, 与 相交于点 ,有以下结论:① ;② ;③点 在 的平分线上.其中正确的是
A. ①② B. ①③ C. ②③ D. ①②③
7. 如图,已知钝角 ,老师按如下步骤尺规作图:
步骤 :以 为圆心, 的长为半径画弧①;
步骤 :以 为圆心, 的长为半径画弧②,交弧①于点 ;
步骤 :连接 ,交 延长线于点 .
小明说:图中的 且平分 .
小丽说:图中 平分 .
小强说:图中点 为 的中点.
你认为
A. 小明说的对 B. 小丽说的对
C. 小强说的对 D. 他们说的都不对
8. 已知 (),用尺规作图的方法在 上确定一点 ,使 ,则符合要求的作图痕迹是
A. B.
C. D.
9. 如图,在 中,,,,垂足为 , 与 关于直线 对称,点 的对称点是点 ,则 的度数为
A. B. C. D.
10. 老师让 个学生猜一猜这次考试中 个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗
A. 甲 B. 乙 C. 丙 D. 丁
11. 如图,在 中,,,, 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是
A. B. C. D.
12. 如图,在 中,,,, 是 的中点,直线 经过点 ,,,垂足分别为 ,,则 的最大值为
A. B. C. D.
二、(共6小题;每小题4分,共24分)
13. 命题“等腰三角形两底角的平分线相等”的逆命题是 .
14. 如图,将两个完全相同的含有 角的三角板拼接在一起,则拼接后的 的形状是 .
15. 用反证法证明“圆内不是直径的两条弦,不能互相平分”时,假设 .
16. 如图,在 中, 和 的平分线相交于点 ,过点 作 ,分别交边 , 于点 ,.如果 ,,那么 的周长为 .
17. 如图,在 中,,,,,, 两点分别在 和过点 且垂直于 的射线 上运动,要使 和 全等,则 .
18. 如图, 中,,,,则 .
三、(共7小题;共60分)
19. (6分)如图,画出 的高 ,,.
20. (8分)已知 的三边长分别为 ,,.
(1)若 ,, 满足 ,试判断 的形状;
(2)若 ,,且 为整数,求 周长的最大值.
21. (10分)阅读理解
折纸,常常能为证明一个命题提供思路和方法.
例如,在 中,(图 ①),怎样证明 呢
思路:
把 沿 的平分线 翻折,如图 ②,因为 ,所以点 落在 上的点 处.于是,由 ,可得 .
证明:
作 平分 交 于点 ,在 上截取 ,连接 .因为 平分 ,所以 .在 和 中, 所以 ,所以 .因为 ,所以 .
解决问题
在 中,, 为线段 上一点.
(1)如图 ③,当 时,求证:;
(2)如图 ④,当 平分 时,判断 , 和 的数量关系并证明.
22. (8分)【拓展阅读】
无理数的发现
在 多年前,古希腊毕达哥拉斯学派弟子希帕斯发现:以一个正方形的边为长度单位去量这个正方形的对角线,这一对角线的长度不能用有理数表示,从而发现了无理数 ,导致了第一次数学危机.后来,古希腊人终于正视了希帕斯的发现,并进一步给出了证明过程.
阅读材料
假设 是一个有理数,那么可得 ,其中 , 是整数, 与 互素,且 ,则 ,即 , 是 的倍数.再设 ,其中 是整数,则 ,即 , 是 的倍数.那么 与 不互素,与前面假设 与 互素相矛盾.因此 不可能是一个有理数.
【任务】
(1)材料中证明 是无理数的方法是: .
(2)模仿材料中的证明方法,请判断 是否为无理数,并给出理由.
23.(8分) 如图,在气象站台 的正西方向 千米的 处有一台风中心,该台风中心以每小时 千米的速度沿北偏东 的 方向移动,在距离台风中心 千米内的地方都要受到其影响.
(1)台风中心在移动过程中,与气象台 的最短距离是多少
(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长
24. (8分)如图,已知在 中,,, 是 边上的中线, 是 的垂直平分线,交 于点 ,交 于点 .求 的值.
25. (12分)已知 的两个顶点分别为 ,,顶点 在直线 : 上.
(1)若 ,求点 的坐标.
(2) 面积为 ,设点 坐标 ,求 与 函数关系式.
(3)在直线 上是否存在点 ,使得 是直角三角形.若存在,求出点 坐标;若不存在,说明理由.
答案
一
1. B
2. D
3. D
4. C
5. C
6. D
7. A
【解析】如图,连接 ,,
,,
点 ,点 都在线段 的垂直平分线上,
直线 是线段 的垂直平分线,即 且平分 ,
故小明的说法正确;
而 不一定平分 ,故小丽的说法错误;
点 不一定为 的中点,故小强的说法错误.故选A.
8. D
【解析】由选项D的作法知,点 在线段 的垂直平分线上,
,
.
9. A
10. C
【解析】假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好.
11. C
【解析】如图,过点 作 于点 ,交 于点 ,过点 作 于点 ,
是 的平分线,
,这时 有最小值,即 的长度,
,,,
,
,
,
即 的最小值为 .
12. A
【解析】如图,过点 作 于点 ,过点 作 于点 ,
在 中,
,,
,,
在 中,,
,
点 为 中点,
,
在 与 中,
,
,
延长 ,过点 作 于点 ,
可得 ,
在 中,,
当直线 时,最大值为 ,
综上所述, 的最大值为 .
二
13. 有两条角平分线相等的三角形是等腰三角形
14. 等边三角形
15. 圆内不是直径的两条弦,能互相平分
【解析】利用反证法证明时,先假设命题的结论不成立,即本题假设“圆内不是直径的两条弦,能互相平分”.
16.
17. 或
【解析】当 时,.
在 与 ,
;
当点 与点 重合时,,
在 与 中,
.
综上所述,.
18.
三
19. 如图所示:
20. (1) ,
,,
,,
,
为等边三角形.
(2) ,,
,
为整数,
,
周长最大为 ,即周长最大为 .
21. (1) 在 上截取一点 使得 ,连接 ,如图 ① 所示.
,
,
在 和 中,
,
,,
,
,
,
,
,
,
,
.
(2) ,理由如下:
在 上截取一点 使得 ,连接 ,如图 ② 所示,
平分 ,
,
在 和 中,
,
,,
,
,
,
,
,
,
,
.
22. (1) 反证法
(2) 是无理数.
理由:假设 是一个有理数,那么可得 ,其中 , 是整数, 与 互素,且 ,则 ,即 , 是 的倍数.再设 ,其中 是整数,则 ,即 , 是 的倍数.那么 与 不互素,与前面假设 与 互素相矛盾.因此 不可能是一个有理数.
23. (1) 略
(2) 略
24. 略
25. (1)
(2) 当 时,;当 时,.
(3) 存在,,,,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
