7.1.1条件概率 课件(共31张PPT)
文档属性
| 名称 | 7.1.1条件概率 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 21:28:02 | ||
图片预览











文档简介
(共31张PPT)
第七章 随机变量及其分布
章前导入
概率是随机事件发生可能性大小的度量。在必修课程的概率的学习中,我们结合课古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质。
本章将在此的基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式,并用它们计算较为复杂事件的概率。
章前导入
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章,我们还将把随机事件的结果数量化,引入随机变量的概念。对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究。
对于连续型随机变量,我们只研究服从正态分布的情况。并通过用随机变量藐视和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点。
第七章 随机变量及其分布
7.1条件概率与全概率公式
7.1.1条件概率
课程标准
(1)结合古典概型,了解条件概率,能计算简单随机事件的条件概率;
(2)结合古典概型,了解条件概率与独立性之间的关系;
(3)结合古典概型,会利用全概率公式计算概率。了解贝叶斯公式;
复习回顾
回顾1 什么是古典概型?我们是怎么计算古典概型的概率?
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
古典概型满足:有限性、等可能性
新课导入
在必修“概率”一章的学习中,我们遇到过求同一试验中两个事件与同时发生(积事件)的概率的问题.
当事件与相互独立时,有。
如果事件与不独立,如何表示积事件的概率呢?
下面我们从具体问题入手.
一
二
三
教学目标
了解条件概率的概念,区分与
理解并掌握条件概率公式
能利用条件概率公式计算相关问题
教学目标
难点
重点
新知探究
探究一:条件概率的概念及公式
新知讲解
实例1 在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员, 那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
随机选择一人做代表, 则样本空间包含45个等可能的样本点 .
用表示事件“选到团员”, 表示事件“选到男生”, 根据表中的数据可以得出:
n(Ω)=45, n (A)=30, n(B)=25.
(1)根据古典概型知识可知,选到男生的概率
新知讲解
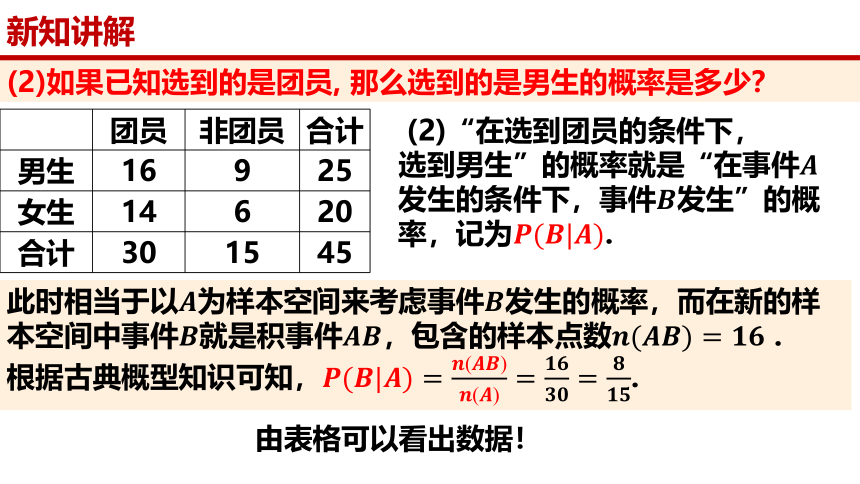
(2)如果已知选到的是团员, 那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
(2)“在选到团员的条件下,
选到男生”的概率就是“在事件发生的条件下,事件发生”的概率,记为.
此时相当于以为样本空间来考虑事件发生的概率,而在新的样本空间中事件就是积事件,包含的样本点数 .
根据古典概型知识可知,.
由表格可以看出数据!
新知讲解
实例2:假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭 . 随机选择一个家庭 , 那么:
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
观察两个小孩的性别, 用表示男孩, 表示女孩, 则样本空间 , 且所有样本点是等可能的.
用表示事件“选择的家庭中有女孩”,表示事件“选择的家庭中两个孩子都是女孩”, 则.
(1)根据古典概型知识可知,该家庭中两个小孩都是女孩的概率
新知讲解
实例2: (2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
则样本空间, 用表示事件“选择的家庭中有女孩”,表示事件“选择的家庭中两个孩子都是女孩”, 则.
(2)“在选择的家庭有女孩的条件下 , 两个小孩都是女孩”的概率就是“在事件发生的条件下 , 事件发生”的概率 , 记为 .
此时成为样本空间 , 事件就是积事件.
根据古典概型知识可知,
实例1,实例2说明了什么呢?
新知讲解
在上面两个问题中,在事件发生的条件下,事件发生的概率都是。这个结论对于一般的古典概型仍然成立.
事实上, 如下图所示, 若已知事件发生, 则成为样本空间.
此时, 事件发生的概率是包含的样本点数与包含的样本点数的比值, 即。
AB
A
B
Ω
概念生成
一般地, 设为两个随机事件, 且,
我们称为在事件发生的条件下, 事件发生的条件概率,简称条件概率.
AB
A
B
Ω
新知讲解
在实例1和实例2中, 都有.
一般地,与不一定相等.
问题1 如果与相等,那么事件与应满足什么条件?
直观上看, 当事件与相互独立时, 事件发生与否不影响事件发生的概率,这等价于成立.
事实上, 若事件与相互独立,
即,且
新知讲解
即 当事件相互独立时, 事件发生与否不影响事件发生的概率,这等价于成立:
反之,若,且,则:
所以,即事件A与B相互独立
新知讲解
问题2 对于任意两个事件与, 如果已知与, 如何计算呢?
,我们称为概率的乘法公式 .
新知探究
探究二:条件概率公式的应用
例题讲解
例1 在5道试题中有3道代数题和2道几何题, 每次从中随机抽出1道题,抽出的题不再放回. 求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下, 第2次抽到几何题的概率.
分析 : 如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件, 那么问题(1)就是积事件的概率, 问题(2)就是条件概率.
可以先求积事件的概率, 再用条件概率公式求条件概率; 也可以先求条件概率, 再用乘法公式求积事件的概率.
新知讲解
问题3 与,它们相同吗?为什么?
为在事件发生的条件下, 事件发生的条件概率
为在事件发生的条件下, 事件发生的条件概率
AB
A
B
Ω
例题讲解
设=“第1次抽到代数题”, =“第2次抽到几何题”.
(1)第1次抽到代数题且第2次抽到几何题”就是事件. 从5道试题中每次不放回地随机抽取2道(抽2题,分先后;即带有顺序),试验的样本空间包含20个等可能的样本点,
即
又
例题讲解
(2)“在第1次抽到代数题的条件下, 第2次抽到几何题”的概率就是事件发生的条件下,事件发生的概率.
因为(古典概型公式)
利用条件概率公式,得
判断概型,
选对概率公式
新知讲解
方法1:一种是基于样本空间,先计算 和 ,再利用条件概率公式求;
求条件概率有两种方法:
方法2:另一种是根据条件概率的直观意义,增加了“发生”的条件后,样本空间缩小为,求就是以为样本空间计算的概率。
新知讲解
条件概率只是缩小了样本空间, 因此条件概率同样具有概率的性质. 设,则
(1);
(2)如果和是两个互斥事件
则 ;
(3)设B和互为对立事件,则
新知讲解
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张 . 他们中奖的概率与抽奖的次序有关吗?
分析:要知道中奖概率是否与抽奖次序有关,只要考察甲、乙、丙3名同学的中奖概率是否相等 .
因为只有1张有奖, 所以“乙中奖”等价于“甲没中奖且乙中奖”,
“丙中奖”等价于“甲和乙都没中奖”,利用乘法公式可求出乙、丙中奖的概率.
例题讲解
解: 用分别表示甲、乙、丙中奖的事件,则
因为,“乙中奖”等价于“甲没中奖且乙中奖”,即
“丙中奖”等价于“甲和乙都没中奖”,
因为, 所以中奖的概率与抽奖的次序无关.
抽签是公平的
新知讲解
例3 银行储蓄卡的密码由6位数字组成 . 某人在银行自助取款机上取钱时,忘记了码的最后1位数字. 求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)若记得密码的最后1位是偶数, 不超过2次就按对的概率.
分析: 最后1位密码“不超过2次就按对”等价于“第1次按对,或者第1次按错第2次按对”.
因此,可以先把复杂事件用简单事件表示,再利用概率性质求解.
例题讲解
解: (1)设=“第次按对密码”,则事件“不超过2次就按对密码”可表示为
事件与事件互斥, 由概率的加法公式及乘法公式, 得
=
因此, 任意按最后1位数字, 不超过2次就按对的概率为
(2)设B=“最后1位密码为偶数”
则=
因此, 如果记得密码的最后1位是偶数, 不超过2次就按对的概率为 .
小结
一般地, 设为两个随机事件, 且,
我们称为在事件发生的条件下, 事件发生的条件概率,简称条件概率.
条件概率的定义:
小结
条件概率的性质
(1);
(2)如果和是两个互斥事件
则 ;
(3)设B和互为对立事件,则
第七章 随机变量及其分布
章前导入
概率是随机事件发生可能性大小的度量。在必修课程的概率的学习中,我们结合课古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质。
本章将在此的基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式,并用它们计算较为复杂事件的概率。
章前导入
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章,我们还将把随机事件的结果数量化,引入随机变量的概念。对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究。
对于连续型随机变量,我们只研究服从正态分布的情况。并通过用随机变量藐视和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点。
第七章 随机变量及其分布
7.1条件概率与全概率公式
7.1.1条件概率
课程标准
(1)结合古典概型,了解条件概率,能计算简单随机事件的条件概率;
(2)结合古典概型,了解条件概率与独立性之间的关系;
(3)结合古典概型,会利用全概率公式计算概率。了解贝叶斯公式;
复习回顾
回顾1 什么是古典概型?我们是怎么计算古典概型的概率?
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
古典概型满足:有限性、等可能性
新课导入
在必修“概率”一章的学习中,我们遇到过求同一试验中两个事件与同时发生(积事件)的概率的问题.
当事件与相互独立时,有。
如果事件与不独立,如何表示积事件的概率呢?
下面我们从具体问题入手.
一
二
三
教学目标
了解条件概率的概念,区分与
理解并掌握条件概率公式
能利用条件概率公式计算相关问题
教学目标
难点
重点
新知探究
探究一:条件概率的概念及公式
新知讲解
实例1 在班级里随机选择一人做代表:
(1)选到男生的概率是多少?
(2)如果已知选到的是团员, 那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
随机选择一人做代表, 则样本空间包含45个等可能的样本点 .
用表示事件“选到团员”, 表示事件“选到男生”, 根据表中的数据可以得出:
n(Ω)=45, n (A)=30, n(B)=25.
(1)根据古典概型知识可知,选到男生的概率
新知讲解
(2)如果已知选到的是团员, 那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
(2)“在选到团员的条件下,
选到男生”的概率就是“在事件发生的条件下,事件发生”的概率,记为.
此时相当于以为样本空间来考虑事件发生的概率,而在新的样本空间中事件就是积事件,包含的样本点数 .
根据古典概型知识可知,.
由表格可以看出数据!
新知讲解
实例2:假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭 . 随机选择一个家庭 , 那么:
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
观察两个小孩的性别, 用表示男孩, 表示女孩, 则样本空间 , 且所有样本点是等可能的.
用表示事件“选择的家庭中有女孩”,表示事件“选择的家庭中两个孩子都是女孩”, 则.
(1)根据古典概型知识可知,该家庭中两个小孩都是女孩的概率
新知讲解
实例2: (2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
则样本空间, 用表示事件“选择的家庭中有女孩”,表示事件“选择的家庭中两个孩子都是女孩”, 则.
(2)“在选择的家庭有女孩的条件下 , 两个小孩都是女孩”的概率就是“在事件发生的条件下 , 事件发生”的概率 , 记为 .
此时成为样本空间 , 事件就是积事件.
根据古典概型知识可知,
实例1,实例2说明了什么呢?
新知讲解
在上面两个问题中,在事件发生的条件下,事件发生的概率都是。这个结论对于一般的古典概型仍然成立.
事实上, 如下图所示, 若已知事件发生, 则成为样本空间.
此时, 事件发生的概率是包含的样本点数与包含的样本点数的比值, 即。
AB
A
B
Ω
概念生成
一般地, 设为两个随机事件, 且,
我们称为在事件发生的条件下, 事件发生的条件概率,简称条件概率.
AB
A
B
Ω
新知讲解
在实例1和实例2中, 都有.
一般地,与不一定相等.
问题1 如果与相等,那么事件与应满足什么条件?
直观上看, 当事件与相互独立时, 事件发生与否不影响事件发生的概率,这等价于成立.
事实上, 若事件与相互独立,
即,且
新知讲解
即 当事件相互独立时, 事件发生与否不影响事件发生的概率,这等价于成立:
反之,若,且,则:
所以,即事件A与B相互独立
新知讲解
问题2 对于任意两个事件与, 如果已知与, 如何计算呢?
,我们称为概率的乘法公式 .
新知探究
探究二:条件概率公式的应用
例题讲解
例1 在5道试题中有3道代数题和2道几何题, 每次从中随机抽出1道题,抽出的题不再放回. 求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下, 第2次抽到几何题的概率.
分析 : 如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件, 那么问题(1)就是积事件的概率, 问题(2)就是条件概率.
可以先求积事件的概率, 再用条件概率公式求条件概率; 也可以先求条件概率, 再用乘法公式求积事件的概率.
新知讲解
问题3 与,它们相同吗?为什么?
为在事件发生的条件下, 事件发生的条件概率
为在事件发生的条件下, 事件发生的条件概率
AB
A
B
Ω
例题讲解
设=“第1次抽到代数题”, =“第2次抽到几何题”.
(1)第1次抽到代数题且第2次抽到几何题”就是事件. 从5道试题中每次不放回地随机抽取2道(抽2题,分先后;即带有顺序),试验的样本空间包含20个等可能的样本点,
即
又
例题讲解
(2)“在第1次抽到代数题的条件下, 第2次抽到几何题”的概率就是事件发生的条件下,事件发生的概率.
因为(古典概型公式)
利用条件概率公式,得
判断概型,
选对概率公式
新知讲解
方法1:一种是基于样本空间,先计算 和 ,再利用条件概率公式求;
求条件概率有两种方法:
方法2:另一种是根据条件概率的直观意义,增加了“发生”的条件后,样本空间缩小为,求就是以为样本空间计算的概率。
新知讲解
条件概率只是缩小了样本空间, 因此条件概率同样具有概率的性质. 设,则
(1);
(2)如果和是两个互斥事件
则 ;
(3)设B和互为对立事件,则
新知讲解
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张 . 他们中奖的概率与抽奖的次序有关吗?
分析:要知道中奖概率是否与抽奖次序有关,只要考察甲、乙、丙3名同学的中奖概率是否相等 .
因为只有1张有奖, 所以“乙中奖”等价于“甲没中奖且乙中奖”,
“丙中奖”等价于“甲和乙都没中奖”,利用乘法公式可求出乙、丙中奖的概率.
例题讲解
解: 用分别表示甲、乙、丙中奖的事件,则
因为,“乙中奖”等价于“甲没中奖且乙中奖”,即
“丙中奖”等价于“甲和乙都没中奖”,
因为, 所以中奖的概率与抽奖的次序无关.
抽签是公平的
新知讲解
例3 银行储蓄卡的密码由6位数字组成 . 某人在银行自助取款机上取钱时,忘记了码的最后1位数字. 求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)若记得密码的最后1位是偶数, 不超过2次就按对的概率.
分析: 最后1位密码“不超过2次就按对”等价于“第1次按对,或者第1次按错第2次按对”.
因此,可以先把复杂事件用简单事件表示,再利用概率性质求解.
例题讲解
解: (1)设=“第次按对密码”,则事件“不超过2次就按对密码”可表示为
事件与事件互斥, 由概率的加法公式及乘法公式, 得
=
因此, 任意按最后1位数字, 不超过2次就按对的概率为
(2)设B=“最后1位密码为偶数”
则=
因此, 如果记得密码的最后1位是偶数, 不超过2次就按对的概率为 .
小结
一般地, 设为两个随机事件, 且,
我们称为在事件发生的条件下, 事件发生的条件概率,简称条件概率.
条件概率的定义:
小结
条件概率的性质
(1);
(2)如果和是两个互斥事件
则 ;
(3)设B和互为对立事件,则
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
