第一章 直角三角形的边角关系单元检测试卷B(含答案)
文档属性
| 名称 | 第一章 直角三角形的边角关系单元检测试卷B(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 19:39:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2022-2023学年九年级(下)第一章直角三角形的边角检测试卷B
(时间120分钟,满分120分)
一、(共12小题;每小题3分,共36分)
1. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
2. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
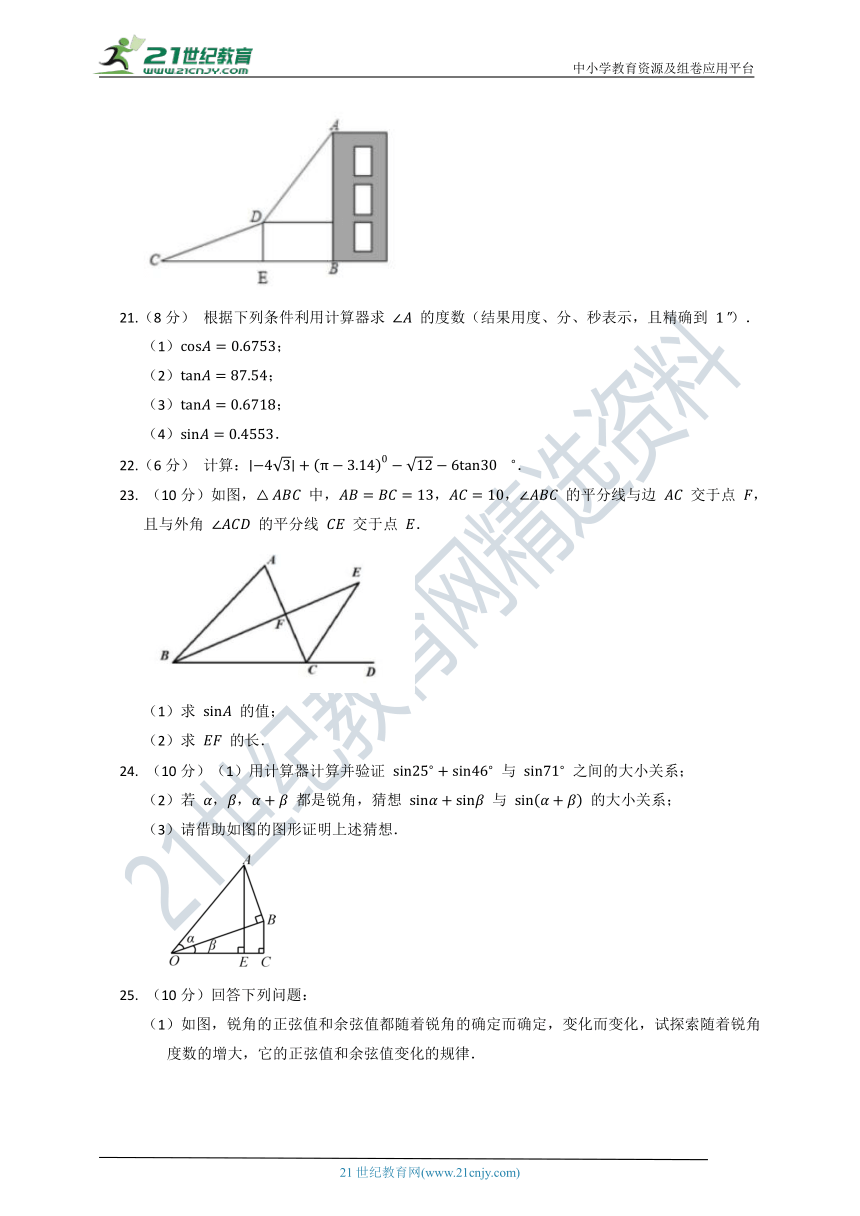
A. B. C. D.
3. 在 中,各边的长度都扩大 倍.那么锐角 的正切值
A. 扩大 倍 B. 扩大 倍 C. 保持不变 D. 缩小 位
4. 如图,河堤横断面的坡比 ,,则坡面 的长为
A. B. C. D.
5. 若等腰三角形底边长为 ,周长为 ,则底角的余弦值等于
A. B. C. D.
6. 在 中,,,,则 的度数是
A. B. C. D.
7. 规定:,,.给出以下四个结论:
();
();
();
().
其中正确的结论的个数为
A. 个 B. 个 C. 个 D. 个
8. 已知菱形的周长为 ,两邻角的度数比为 ,则菱形的面积为
A. B. C. D.
9. 在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道——无障碍通道,如图,线段 表示无障碍通道,线段 表示普通扶梯,其中无障碍通道 的坡度(或坡比)为 ,,,(点 ,,, 均在同一平面内),则垂直升降电梯 的高度约为
A. B. C. D.
10. 利用投影仪把 各边的长度都扩大为原来的 倍,则锐角 的各三角函数值
A. 都扩大为原来的 倍 B. 都缩小为原来的
C. 没有变化 D. 不能确定
11. 如图,一个人从山脚下的 点出发,沿山坡小路 走到山顶 点.已知坡角为 ,山高 千米.用科学计算器计算小路 的长度,下列按键顺序正确的是
A. \( \boxed{2}\boxed{\div}\boxed{\sin}\boxed{2}\boxed{0}\boxed{=} \) B. \(\boxed{2}\boxed{\times}\boxed{\sin}\boxed{2}\boxed{0}\boxed{=}\) C. \(\boxed{2}\boxed{\div}\boxed{\cos}\boxed{2}\boxed{0}\boxed{=}\) D. \(\boxed{2}\boxed{\times}\boxed{\tan}\boxed{2}\boxed{0}\boxed{=}\)
12. 如图,坡角为 的斜坡上两根电线杆间的坡面距离为 ,则这两根电线杆间的水平距离为
A. B. C. D.
二、(共6小题;每小题4分,共24分)
13. 在 中,,如果 ,那么 .
14. 如果一个斜坡的坡度 ,那么该斜坡的坡角为 度.
15. 在 中,,若 ,则 .
16. 如图,在 中,,,点 , 分别在 边和 边上,沿着直线 翻折 ,点 落在 边上,记为点 ,如果 ,则 .
17. 一般地,当 , 为任意角时, 与 的值可以用下面的公式求得:
;
.
例如 .
类似地,可以求得 的值是 .
18. 如图, 中,,, 于点 ,将 绕点 逆时针旋转,旋转角的大小与 相等,如果点 , 旋转后分别落在点 , 的位置,那么 的正切值是 .
三、(共7小题;共60分)
19. (8分)《雁栖塔》位于怀柔“北京雁栖湖国际会都中心”所处大岛西南部突出部位的半岛上,是“北京雁栖湖国际会都中心”的标志性建筑,也是整个雁栖湖风景区的标志性建筑.
某校数学课外小组为了测量《雁栖塔》(底部可到达)的高度,准备了如下的测量工具:
①平面镜,②皮尺,③长为 米的标杆,④高为 的测角仪(测量仰角、俯角的仪器).第一组选择用②④做测量工具;第二组选用②③做测量工具;第三组利用自身的高度并选用①②做测量工具,分别画出如下三种测量方案示意图.
(1)请你判断如下测量方案示意图各是哪个小组的,在测量方案示意图下方的括号内填上小组名称;
(2)选择其中一个测量方案示意图,写出求《雁栖塔》高度的思路.
20. (8分)如图,为了测量建筑物 的高度,先从与建筑物 的底部 点水平相距 米的点 处出发,沿斜坡 行走至坡顶 处,斜坡 的坡度 ,坡顶 到 的距离 米,在点 处测得建筑物顶端 点的仰角为 ,点 ,,,, 在同一平面内,根据测量数据,请计算建筑物 的高度(结果精确到 米).(参考数据:,,)
21.(8分) 根据下列条件利用计算器求 的度数(结果用度、分、秒表示,且精确到 ).
(1);
(2);
(3);
(4).
22.(6分) 计算:.
23. (10分)如图, 中,,, 的平分线与边 交于点 ,且与外角 的平分线 交于点 .
(1)求 的值;
(2)求 的长.
24. (10分)(1)用计算器计算并验证 与 之间的大小关系;
(2)若 ,, 都是锐角,猜想 与 的大小关系;
(3)请借助如图的图形证明上述猜想.
25. (10分)回答下列问题:
(1)如图,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律试比较 ,,,, 这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“”“”或“”);
若 ,则 ;
若 ,则 ;
若 ,则 .
答案
一
1. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
2. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
3. C
【解析】如图,
在 中,,则 ,
,
在 中,各边的长度都扩大 倍.那么锐角 的正切值保持不变,故选:C.
4. C
5. A
6. D
7. C
【解析】(),故此结论正确;
(),故此结论正确;
()
故此结论正确;
()
故此结论错误.
8. D
【解析】如图,
两邻角度数之比为 ,
,.
菱形的周长为 ,
边长 ,
菱形的对角线 ,,
.
9. B
【解析】如图,延长 交 的延长线于点 ,
由 的坡度(或坡比)为 ,得 .
设 ,,
在 中,由勾股定理,得 ,
即 ,解得 ,
,,
,
由 ,得 ,
解得 ,
.
故选B.
10. C
【解析】 各边的长度都扩大为原来的五倍,
扩大后的三角形与原三角形相似,即锐角 的度数不变,
锐角 的各三角函数值没有变化.
11. A
【解析】在 中,
因为 ,
所以 (米),
则按键顺序为 \(\boxed{2}\boxed{\div}\boxed{\sin}\boxed{2}\boxed{0}\boxed{=}\).
12. B
【解析】如图(),
由题意得 ,在 中,,,
.故选B.
二
13.
14.
【解析】,
坡角 .
故答案为 .
15.
16. 或
【解析】如图,过点 作 于点 .
在 中,,,
,,
,
是等腰直角三角形,
,
设 ,则 ,,
沿着直线 翻折 ,点 落在 边上,记为点 ,
,
在 中,,
即 ,
解得 .
17.
【解析】 .
18.
三
19. (1) 二组,一组,三组
(2) 一图思路:①分别测出在同一时刻标杆 和《雁栖塔》 的影长 , ;
②由 ,利用 求出 的值.
二图思路:①用测角仪测出 的角度;②用皮尺测量 的长;
③ ;
④ .
三图思路:①用皮尺分别测量 , , 的长;
②由 ,利用 求出 的值.
20. 因为斜坡 的坡度(或坡比)为 ,
所以 ,
因为 米,
所以 米,
因为 米,
所以 (米),
所以 (米).
答:建筑物 的高度为 米.
21. (1) 按键顺序为 ,
结果:,所以 .
(2) 按键顺序为 ,
结果:,所以 .
(3) 按键顺序为 ,
结果:,所以 .
(4) 按键顺序为 ,
结果:,所以 .
22.
23. (1) .
(2) 作 ,
设 ,
,
,
,
.
24. (1) ,
,
,
.
(2) .
(3) ,.
,
,
.
,
,
.
25. (1) 题图()中,令 , 于点 , 于点 , 于点 ,
显然有:,.
,,,
而 ,
.
题图()中,在 中,,
,,,
,
.
即 .
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2) 由()可知:
;
.
(3) ;;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-2023学年九年级(下)第一章直角三角形的边角检测试卷B
(时间120分钟,满分120分)
一、(共12小题;每小题3分,共36分)
1. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
2. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
3. 在 中,各边的长度都扩大 倍.那么锐角 的正切值
A. 扩大 倍 B. 扩大 倍 C. 保持不变 D. 缩小 位
4. 如图,河堤横断面的坡比 ,,则坡面 的长为
A. B. C. D.
5. 若等腰三角形底边长为 ,周长为 ,则底角的余弦值等于
A. B. C. D.
6. 在 中,,,,则 的度数是
A. B. C. D.
7. 规定:,,.给出以下四个结论:
();
();
();
().
其中正确的结论的个数为
A. 个 B. 个 C. 个 D. 个
8. 已知菱形的周长为 ,两邻角的度数比为 ,则菱形的面积为
A. B. C. D.
9. 在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道——无障碍通道,如图,线段 表示无障碍通道,线段 表示普通扶梯,其中无障碍通道 的坡度(或坡比)为 ,,,(点 ,,, 均在同一平面内),则垂直升降电梯 的高度约为
A. B. C. D.
10. 利用投影仪把 各边的长度都扩大为原来的 倍,则锐角 的各三角函数值
A. 都扩大为原来的 倍 B. 都缩小为原来的
C. 没有变化 D. 不能确定
11. 如图,一个人从山脚下的 点出发,沿山坡小路 走到山顶 点.已知坡角为 ,山高 千米.用科学计算器计算小路 的长度,下列按键顺序正确的是
A. \( \boxed{2}\boxed{\div}\boxed{\sin}\boxed{2}\boxed{0}\boxed{=} \) B. \(\boxed{2}\boxed{\times}\boxed{\sin}\boxed{2}\boxed{0}\boxed{=}\) C. \(\boxed{2}\boxed{\div}\boxed{\cos}\boxed{2}\boxed{0}\boxed{=}\) D. \(\boxed{2}\boxed{\times}\boxed{\tan}\boxed{2}\boxed{0}\boxed{=}\)
12. 如图,坡角为 的斜坡上两根电线杆间的坡面距离为 ,则这两根电线杆间的水平距离为
A. B. C. D.
二、(共6小题;每小题4分,共24分)
13. 在 中,,如果 ,那么 .
14. 如果一个斜坡的坡度 ,那么该斜坡的坡角为 度.
15. 在 中,,若 ,则 .
16. 如图,在 中,,,点 , 分别在 边和 边上,沿着直线 翻折 ,点 落在 边上,记为点 ,如果 ,则 .
17. 一般地,当 , 为任意角时, 与 的值可以用下面的公式求得:
;
.
例如 .
类似地,可以求得 的值是 .
18. 如图, 中,,, 于点 ,将 绕点 逆时针旋转,旋转角的大小与 相等,如果点 , 旋转后分别落在点 , 的位置,那么 的正切值是 .
三、(共7小题;共60分)
19. (8分)《雁栖塔》位于怀柔“北京雁栖湖国际会都中心”所处大岛西南部突出部位的半岛上,是“北京雁栖湖国际会都中心”的标志性建筑,也是整个雁栖湖风景区的标志性建筑.
某校数学课外小组为了测量《雁栖塔》(底部可到达)的高度,准备了如下的测量工具:
①平面镜,②皮尺,③长为 米的标杆,④高为 的测角仪(测量仰角、俯角的仪器).第一组选择用②④做测量工具;第二组选用②③做测量工具;第三组利用自身的高度并选用①②做测量工具,分别画出如下三种测量方案示意图.
(1)请你判断如下测量方案示意图各是哪个小组的,在测量方案示意图下方的括号内填上小组名称;
(2)选择其中一个测量方案示意图,写出求《雁栖塔》高度的思路.
20. (8分)如图,为了测量建筑物 的高度,先从与建筑物 的底部 点水平相距 米的点 处出发,沿斜坡 行走至坡顶 处,斜坡 的坡度 ,坡顶 到 的距离 米,在点 处测得建筑物顶端 点的仰角为 ,点 ,,,, 在同一平面内,根据测量数据,请计算建筑物 的高度(结果精确到 米).(参考数据:,,)
21.(8分) 根据下列条件利用计算器求 的度数(结果用度、分、秒表示,且精确到 ).
(1);
(2);
(3);
(4).
22.(6分) 计算:.
23. (10分)如图, 中,,, 的平分线与边 交于点 ,且与外角 的平分线 交于点 .
(1)求 的值;
(2)求 的长.
24. (10分)(1)用计算器计算并验证 与 之间的大小关系;
(2)若 ,, 都是锐角,猜想 与 的大小关系;
(3)请借助如图的图形证明上述猜想.
25. (10分)回答下列问题:
(1)如图,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律试比较 ,,,, 这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“”“”或“”);
若 ,则 ;
若 ,则 ;
若 ,则 .
答案
一
1. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
2. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
3. C
【解析】如图,
在 中,,则 ,
,
在 中,各边的长度都扩大 倍.那么锐角 的正切值保持不变,故选:C.
4. C
5. A
6. D
7. C
【解析】(),故此结论正确;
(),故此结论正确;
()
故此结论正确;
()
故此结论错误.
8. D
【解析】如图,
两邻角度数之比为 ,
,.
菱形的周长为 ,
边长 ,
菱形的对角线 ,,
.
9. B
【解析】如图,延长 交 的延长线于点 ,
由 的坡度(或坡比)为 ,得 .
设 ,,
在 中,由勾股定理,得 ,
即 ,解得 ,
,,
,
由 ,得 ,
解得 ,
.
故选B.
10. C
【解析】 各边的长度都扩大为原来的五倍,
扩大后的三角形与原三角形相似,即锐角 的度数不变,
锐角 的各三角函数值没有变化.
11. A
【解析】在 中,
因为 ,
所以 (米),
则按键顺序为 \(\boxed{2}\boxed{\div}\boxed{\sin}\boxed{2}\boxed{0}\boxed{=}\).
12. B
【解析】如图(),
由题意得 ,在 中,,,
.故选B.
二
13.
14.
【解析】,
坡角 .
故答案为 .
15.
16. 或
【解析】如图,过点 作 于点 .
在 中,,,
,,
,
是等腰直角三角形,
,
设 ,则 ,,
沿着直线 翻折 ,点 落在 边上,记为点 ,
,
在 中,,
即 ,
解得 .
17.
【解析】 .
18.
三
19. (1) 二组,一组,三组
(2) 一图思路:①分别测出在同一时刻标杆 和《雁栖塔》 的影长 , ;
②由 ,利用 求出 的值.
二图思路:①用测角仪测出 的角度;②用皮尺测量 的长;
③ ;
④ .
三图思路:①用皮尺分别测量 , , 的长;
②由 ,利用 求出 的值.
20. 因为斜坡 的坡度(或坡比)为 ,
所以 ,
因为 米,
所以 米,
因为 米,
所以 (米),
所以 (米).
答:建筑物 的高度为 米.
21. (1) 按键顺序为 ,
结果:,所以 .
(2) 按键顺序为 ,
结果:,所以 .
(3) 按键顺序为 ,
结果:,所以 .
(4) 按键顺序为 ,
结果:,所以 .
22.
23. (1) .
(2) 作 ,
设 ,
,
,
,
.
24. (1) ,
,
,
.
(2) .
(3) ,.
,
,
.
,
,
.
25. (1) 题图()中,令 , 于点 , 于点 , 于点 ,
显然有:,.
,,,
而 ,
.
题图()中,在 中,,
,,,
,
.
即 .
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2) 由()可知:
;
.
(3) ;;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
