2022-2023学年北师大版 八年级数学下册 一元一次不等式和一元一次不等式组(单元小结)PPT(28张PPT)
文档属性
| 名称 | 2022-2023学年北师大版 八年级数学下册 一元一次不等式和一元一次不等式组(单元小结)PPT(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 16:55:41 | ||
图片预览








文档简介
新课标 北师大版
八年级下册
第二章 一元一次不等式和一元一次不等式组
单元小结
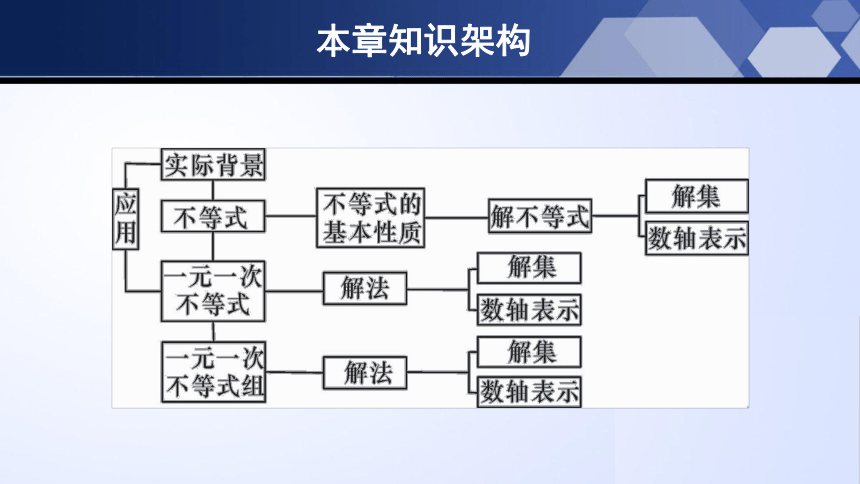
本章知识架构
知识专题
知识点一:概念学习
概念一:不等式
定义:一般地,用符号“<”(或“≤”),“>” (或“≥”),“≠”连接的式子叫做不等式.
知识专题
概念二:一元一次不等式
左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1的不等式,叫做一元一次不等式.
特点:
(1)左右两边都是整式;
(2)只含有一个未知数;
(3)未知数的最高次数是1.
知识专题
概念3:一元一次不等式组
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
条件:
(1)同一未知数(只有一种字母);
(2)一元一次不等式.
知识专题
概念4:不等式(组 )的解或解集
能使不等式成立的未知数的解,叫做不等式的解.
(1)一个含有未知数的不等式的所有解,组成这个不等式的解集;
(2)不等式组中各个不等式的解集的公共部分叫做不等式组的解集;
知识专题
概念4:不等式(组 )的解或解集
在数轴上表示解集
“>”或“<”画空心圆圈,表示不包括某点
“≥”或“≤”画实心圆点,表示包括某点
大于向右画,小于向左画.
知识专题
知识点二:不等式的基本性质
1.不等式的两边都加(或减)同一个整式,不等号的方向不变.
2.不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
3.不等式的两边都乘(或除以)同一个负数,不等号的方向改变。
知识专题
知识点三:解法
(一)一元一次不等式的解法
解一元一次不等式的步骤:
(1)去分母; (2)去括号; (3)移项;
(4)合并同类项;(5)系数化1。
知识专题
注意:
(1)去分母时,不要漏乘常数项,分子是多项式时要加括号;
(2)移项时,要变号;
(3)系数化为1时,不等式的两边都乘或除以同一个负数,不等号的方向要改变.
知识专题
(二)一元一次不等式组的解法
解一元一次不等式组的步骤:
(1)求不等式组中各个不等式的解集;
(2)利用数轴,找出不等式解集的公共部分;
(3)写出不等式组的解集。
知识专题
一元一次不等式组的解集的确定方法有两种:
①利用数轴,②利用口诀,如下表所示:
知识专题
知识点四:应用
(一)一元一次不等式的应用
(二)一元一次不等式组的应用
解题步骤:审、设、列、解、验、答
关键字:
“至少”、“不低于”、“不超过”、“最多”
知识专题
(三)一元一次不等式组与一次函数的应用
一元一次不等式kx+b>0与一次函数y=kx+b的联系:
求ax+b>0(或<0)(a, b是常数,a≠0)的解集
函数y=ax+b(a≠0)的函数值大于0(或小于0)时,x的取值范围
从数的角度看
知识专题
(三)一元一次不等式组与一次函数的应用
一元一次不等式kx+b>0与一次函数y=kx+b的联系:
求ax+b>0(或<0)(a, b是常数,a≠0)的解集
直线y=ax+b(a≠0)在x轴上方(或下方)的部分,x的取值范围
从形的角度看
ax+b>cx+d(或ax+b一次函数y1=ax+b和y2=cx+d相应的函数值y1>y2(或y12.用一次函数图象确定一元一次不等式ax+b>cx+d
(或ax+b知识专题
解此类问题的一般步骤是:
(1)根据已知条件,列出两种方案的一次函数表达式;
(2)根据两个一次函数的大小关系(三种)分别求得相应的x值;
(3)比较所得结果,根据题目要求作出决策即可.
一元一次不等式与一次函数在方案决策型问题中的应用
知识专题
考点专练
1、在数学表达式:(1)-3<0.(2)3x+5>0.(3)x2-6.(4)x=-2.(5)y≠0.(6)x≥50中,不等式的个数是( )
A.2个 B.3个 C.4个 D.5个
考点一:不等式概念
【解析】根据不等式的定义,只要含有不等号的式子就是不等式,所以(1),(2),(5),(6)为不等式,共有4个.
C
考点专练
【特别提醒】
不等式(1)定义:用符号“<”(“≤”),“>”(“≥”) ,“≠”连接的式子.
(2)特征:含有不等号.
考点专练
2、若x>-1,则下列各式错误的是 ( )
A.3x>-3 B.-2x<2 C.x+1>0 D.1-x>2
【解析】由不等式性质2知,A正确; 由性质3知,B正确;由性质1知,C正确;在x>-1两边同乘-1,得-x<1,在-x<1两边同时加上1,得1-x<2,故D错误.
考点二:不等式的基本性质
D
考点专练
【特别提醒】
基本性质1:如果a >?b,那么a±c >?b±c.
基本性质2:如果a >?b,c >?0,那么ac>bc;????????>????????.
基本性质3:如果a >?b,c <?0,那么ac<bc; ????????<????????.
?
考点专练
2
3
1
4
5
6
0
-1
-2
解:去分母,得: 3(2x-3)≤x+1
去括号,得: 6x-9≤x+1
移项, 6x-x≤1+9
合并同类项得: 5x≤10
系数化为1,得: x≤2
考点三:一元一次不等式的解法及解的表示
3、解一元一次不等式2x-3≤????+13,并把解集在数轴上表示出来.
?
考点专练
【特别提醒】解一元一次不等式步骤:
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化1.
考点专练
4、小聪用100元钱去购买笔记本和钢笔共15件,已知每本笔记本5元,每支钢笔7元,小聪最多能买多少支钢笔?
解:设小聪买了x支钢笔,则买了(15-x)本笔记本,
7x+5(15-x)≤100,
解得 x≤12.5,
∵x为整数,
∴x的最大值为12.
答:小聪最多能买12支钢笔.
考点四:一元一次不等式解决实际问题
考点专练
考点五:一元一次不等式组的解法
1.解不等式组:
①
②
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
考点专练
考点六:列一元一次不等式组解应用题
6.某校在“五一”期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且有一辆不空也不满.求外出旅游的学生人数是多少?
考点专练
解:设单独租用45座的客车x辆,则单独租用了(x-1)辆60座的客车.
根据题意,得:
解不等式组,得:4<x<8
45x-60(x-2)<60
45x-60(x-2)>0
所以学生数为:225人、270人或315人.
因为,客车数是正整数,所以,x=5或6或7
谢 谢 ~
八年级下册
第二章 一元一次不等式和一元一次不等式组
单元小结
本章知识架构
知识专题
知识点一:概念学习
概念一:不等式
定义:一般地,用符号“<”(或“≤”),“>” (或“≥”),“≠”连接的式子叫做不等式.
知识专题
概念二:一元一次不等式
左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1的不等式,叫做一元一次不等式.
特点:
(1)左右两边都是整式;
(2)只含有一个未知数;
(3)未知数的最高次数是1.
知识专题
概念3:一元一次不等式组
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
条件:
(1)同一未知数(只有一种字母);
(2)一元一次不等式.
知识专题
概念4:不等式(组 )的解或解集
能使不等式成立的未知数的解,叫做不等式的解.
(1)一个含有未知数的不等式的所有解,组成这个不等式的解集;
(2)不等式组中各个不等式的解集的公共部分叫做不等式组的解集;
知识专题
概念4:不等式(组 )的解或解集
在数轴上表示解集
“>”或“<”画空心圆圈,表示不包括某点
“≥”或“≤”画实心圆点,表示包括某点
大于向右画,小于向左画.
知识专题
知识点二:不等式的基本性质
1.不等式的两边都加(或减)同一个整式,不等号的方向不变.
2.不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
3.不等式的两边都乘(或除以)同一个负数,不等号的方向改变。
知识专题
知识点三:解法
(一)一元一次不等式的解法
解一元一次不等式的步骤:
(1)去分母; (2)去括号; (3)移项;
(4)合并同类项;(5)系数化1。
知识专题
注意:
(1)去分母时,不要漏乘常数项,分子是多项式时要加括号;
(2)移项时,要变号;
(3)系数化为1时,不等式的两边都乘或除以同一个负数,不等号的方向要改变.
知识专题
(二)一元一次不等式组的解法
解一元一次不等式组的步骤:
(1)求不等式组中各个不等式的解集;
(2)利用数轴,找出不等式解集的公共部分;
(3)写出不等式组的解集。
知识专题
一元一次不等式组的解集的确定方法有两种:
①利用数轴,②利用口诀,如下表所示:
知识专题
知识点四:应用
(一)一元一次不等式的应用
(二)一元一次不等式组的应用
解题步骤:审、设、列、解、验、答
关键字:
“至少”、“不低于”、“不超过”、“最多”
知识专题
(三)一元一次不等式组与一次函数的应用
一元一次不等式kx+b>0与一次函数y=kx+b的联系:
求ax+b>0(或<0)(a, b是常数,a≠0)的解集
函数y=ax+b(a≠0)的函数值大于0(或小于0)时,x的取值范围
从数的角度看
知识专题
(三)一元一次不等式组与一次函数的应用
一元一次不等式kx+b>0与一次函数y=kx+b的联系:
求ax+b>0(或<0)(a, b是常数,a≠0)的解集
直线y=ax+b(a≠0)在x轴上方(或下方)的部分,x的取值范围
从形的角度看
ax+b>cx+d(或ax+b
(或ax+b
解此类问题的一般步骤是:
(1)根据已知条件,列出两种方案的一次函数表达式;
(2)根据两个一次函数的大小关系(三种)分别求得相应的x值;
(3)比较所得结果,根据题目要求作出决策即可.
一元一次不等式与一次函数在方案决策型问题中的应用
知识专题
考点专练
1、在数学表达式:(1)-3<0.(2)3x+5>0.(3)x2-6.(4)x=-2.(5)y≠0.(6)x≥50中,不等式的个数是( )
A.2个 B.3个 C.4个 D.5个
考点一:不等式概念
【解析】根据不等式的定义,只要含有不等号的式子就是不等式,所以(1),(2),(5),(6)为不等式,共有4个.
C
考点专练
【特别提醒】
不等式(1)定义:用符号“<”(“≤”),“>”(“≥”) ,“≠”连接的式子.
(2)特征:含有不等号.
考点专练
2、若x>-1,则下列各式错误的是 ( )
A.3x>-3 B.-2x<2 C.x+1>0 D.1-x>2
【解析】由不等式性质2知,A正确; 由性质3知,B正确;由性质1知,C正确;在x>-1两边同乘-1,得-x<1,在-x<1两边同时加上1,得1-x<2,故D错误.
考点二:不等式的基本性质
D
考点专练
【特别提醒】
基本性质1:如果a >?b,那么a±c >?b±c.
基本性质2:如果a >?b,c >?0,那么ac>bc;????????>????????.
基本性质3:如果a >?b,c <?0,那么ac<bc; ????????<????????.
?
考点专练
2
3
1
4
5
6
0
-1
-2
解:去分母,得: 3(2x-3)≤x+1
去括号,得: 6x-9≤x+1
移项, 6x-x≤1+9
合并同类项得: 5x≤10
系数化为1,得: x≤2
考点三:一元一次不等式的解法及解的表示
3、解一元一次不等式2x-3≤????+13,并把解集在数轴上表示出来.
?
考点专练
【特别提醒】解一元一次不等式步骤:
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化1.
考点专练
4、小聪用100元钱去购买笔记本和钢笔共15件,已知每本笔记本5元,每支钢笔7元,小聪最多能买多少支钢笔?
解:设小聪买了x支钢笔,则买了(15-x)本笔记本,
7x+5(15-x)≤100,
解得 x≤12.5,
∵x为整数,
∴x的最大值为12.
答:小聪最多能买12支钢笔.
考点四:一元一次不等式解决实际问题
考点专练
考点五:一元一次不等式组的解法
1.解不等式组:
①
②
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
考点专练
考点六:列一元一次不等式组解应用题
6.某校在“五一”期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且有一辆不空也不满.求外出旅游的学生人数是多少?
考点专练
解:设单独租用45座的客车x辆,则单独租用了(x-1)辆60座的客车.
根据题意,得:
解不等式组,得:4<x<8
45x-60(x-2)<60
45x-60(x-2)>0
所以学生数为:225人、270人或315人.
因为,客车数是正整数,所以,x=5或6或7
谢 谢 ~
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
